四旋翼无人机基于图像的抗干扰视觉伺服控制

郑国泉，袁 亮,2，何 巍

(1.新疆大学，乌鲁木齐 830000； 2.北京化工大学，北京 100000)

0 引言

四旋翼无人机(下文简称四旋翼)的用途越来越广泛，对四旋翼飞行控制[1]的研究较为深入，但是在四旋翼视觉伺服领域仍面临诸多困难。当GPS在室内等无信号地区不可用,IMU不能够精确自身角速度和获取位置时，需要结合视觉相机来进行视觉伺服以获取精确的四旋翼线速度、位置等信息。因此，四旋翼的视觉伺服具有重要作用。在设计视觉伺服控制器的过程中需要解决四旋翼线速度信息的获取问题、图像目标特征选取问题，特别还要面对不同程度的内外部干扰问题以及控制器稳定性的问题。

视觉伺服控制主要利用两种方法：基于位置的视觉伺服和基于图像的视觉伺服[2]。文献[3]将位置和图像相互结合提出了混合的视觉伺服方法，利用雅可比矩阵推导图像误差收敛的期望速度，再设计控制器去跟踪实现视觉伺服，设计的步骤相对复杂。基于位置设计的方法中会存在很多动态的误差，如位置估计误差、机体线速度估计误差，这些误差在设计控制器的过程中并未被解决，所以稳定性较差。基于图像的视觉伺服不需要空间位置信息，对相机捕捉图像所拥有的参数有较好的稳定性[4]。基于图像的视觉伺服可以利用实时图像和期望图像特征建立特征误差推导四旋翼的控制输入。文献[5-7]都是选择图像矩特征结合虚拟相机平面，能够更好地解决目标发生尺度变化或旋转变化时效果不佳的问题，但是均未考虑干扰的影响。

本文提出了利用积分反步滑模控制设计四旋翼的基于图像的抗干扰视觉伺服控制器。首先通过虚拟相机平面对无人机空间运动耦合进行解耦，在虚拟相机平面内选择图像矩特征介绍带有扰动的动力学模型。其次，通过反步法设计线速度估计器和特征误差估计器。最后提出积分反步滑模控制方法去设计全局稳定的动态四旋翼抗干扰的视觉伺服控制器，使闭环系统渐近稳定，飞行过程中稳态误差减小，提高了鲁棒性。

1 四旋翼无人机动力学

本章中主要介绍四旋翼的空间动力学模型，假设四旋翼是严格的刚体结构，然后定义两个用来描述四旋翼动力学模型的坐标系，即地球坐标系E和机体坐标系β，如图1所示。

图1 四旋翼无人机结构简图及坐标系

四旋翼在地球坐标系下的空间位置ξ=[x,y,z]T，其姿态为[φ,θ,ψ]T，φ为横滚角，θ为俯仰角，ψ为偏航角；四旋翼在机体坐标系下的角速度为Ω=[Ω1,Ω2,Ω3]T,机体坐标系下四旋翼线速度为Vβ=[V1,V2,V3]T。通过将运动分解成平动和转动，考虑四旋翼内部建模不确定性和外界干扰，利用牛顿-欧拉方程得到四旋翼动力学方程为[8-9]

(1)

式中：R为β→Ε的旋转矩阵；sk(Ω)为反对称矩阵；F为四旋翼上的合外力；U1为四个旋翼产生的总推力；τ为机体坐标系下的力矩；J为四旋翼的转动惯量；g为重力加速度；m为四旋翼质量；E3=e3=[0,0,1]T；Dv为位置通道外部干扰；Dω为姿态通道建模不确定部分。

2 图像特征及动力学模型

四旋翼视觉伺服中图像特征尤为重要，本章将介绍图像特征及其动力学模型。为了更好地描述动力学以及描述图像特征的变化，定义一个与机体坐标系对齐的相机坐标系C。四旋翼上的相机捕捉到的图像在相机坐标系C下也是耦合的。因此，通过假设一个虚拟相机[7]并定义一个虚拟平面V对图像动力学进行解耦，模型如图2所示。

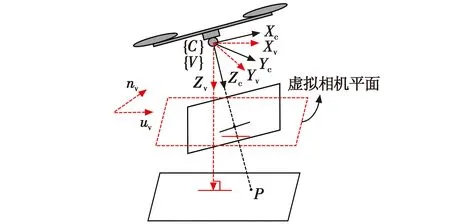
图2 相机平面及虚拟平面

该虚拟相机原点同真实相机一样，虚拟相机平面始终是平行于地面保证它的横滚角和俯仰角始终为零，偏航角和实际相机平面中的偏航角相同。将相机图像平面上的点特征投影到虚拟图像平面上，进而建立出虚拟图像平面上的特征动力学。四旋翼通过相机获取的实时图像在相机真实平面内存在耦合。然后需要通过IMU获取四旋翼的横滚角和俯仰角，再重投影到开始设定的虚拟平面内。在重投影转换之前横滚角和俯仰角会对图像点有影响，但是对整个系统不会造成影响(即该环节构成了一个误差环节)。图像点特征需要转换为图像矩特征，利用图像矩的误差进行视觉伺服控制。

2.1 图像坐标描述

四旋翼通过相机捕捉三维空间中某一点EP，EP点在相机坐标系的坐标cP=[cx,cy,cz]T，在虚拟相机坐标系的坐标vP=[vx,vy,vz]T。

EP点在相机坐标系下的坐标和在虚拟相机坐标系下的坐标可以结合地球坐标系表示为[10]

(2)

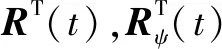
式(2)中vP对时间进行求导得到

(3)

式中，v=[vx,vy,vz]T是虚拟相机坐标系下的机体线速度。(vu,vn)对时间进行求导，然后代入式(3)得到

(4)

前文设计的虚拟平面始终平行于水平面，从式(4)中可以看出，在虚拟相机平面内图像点运动的变化率与四旋翼横滚角以及俯仰角的变化率无关,只与四旋翼线速度和偏航角有关。

2.2 图像矩特征

用于控制四旋翼三维平移运动的图像特征定义为[11]

(5)

(6)

式中，zd为当摄像机处于期望姿势时的深度值。

定义控制四旋翼偏航角qψ为

(7)

3 抗干扰视觉伺服控制器设计

四旋翼抗干扰视觉伺服的系统机构如图3所示，通过外环控制线速度，内环控制角速度。利用视觉相机获取实时图像信息，通过期望图像特征和实时图像特征之间的误差设计抗干扰的视觉伺服控制器，然后推算出总推力以及四旋翼姿态。线速度控制环设计非线性速度观测器，获取线速度信息，最终实现视觉伺服控制。

图3 四旋翼无人机抗干扰视觉伺服系统

3.1 线速度观测器

选择期望的虚拟图像平面的图像特征为

(8)

定义图像误差ε1=q-qd，结合虚拟相机动力学可以得到图像特征动力学模型为

(9)

(10)

(11)

(12)

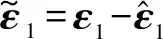
(13)

(14)

(15)

由Lyapunov理论可以证明估计器是收敛稳定的，证明如下。

(16)

定义一个Lyapunov函数

(17)

对式(17)求导后代入式(16)得到

(18)

3.2 积分反步滑模视觉伺服控制器

在设计的稳定的观测器基础上，设计抗干扰的视觉伺服控制器，定义一个Lyapunov函数

(19)

(20)

对误差ε2进行求导得到

(21)

(22)

求导后得到

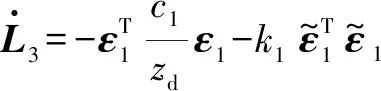
(23)

同理,需要引入中间控制量

(24)

设一个系统滑模函数

(25)

(26)

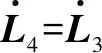
(27)

由此说明系统稳定。以上分析都是基于虚拟坐标系，其中f是四旋翼上的合外力在虚拟坐标系中的表示，所以可以得到

(28)

通过对式(28)求导可得

(29)

(30)

(31)

(32)

4 仿真实验

本文实验为数值仿真，并且主要验证控制器在抗干扰方面的视觉伺服控制能否实现。因此假设在仿真过程中传感器测量的数据不存在噪声和偏移。本章对所提出的控制器进行仿真实验。定义参数为：c1=2，c2=4，c3=4，k1=4，k2=4，k3=0.5，k4=0.5。选取4个地球坐标系下的可视点坐标(单位为m)分别为：(0.25,0.5,0)，(-0.25,0.5,0)，(0.25,-0.5,0)和(-0.25,-0.5,0)。四旋翼质量为m=2 kg，重力加速度为g=9.8 m/s2，然后通过选取J=diag(0.008 1,0.008 1,0.014 2)(单位为kg·m2)作为转动惯量。选取四旋翼地球坐标系中初始位置为ξ=(3,2,-8)(单位为m)，初始欧拉角为(0,0,0.174)(单位为rad)。期望图像矩特征的取值为A*=8×10-7。选取虚拟平面内的干扰为dv=[0.5sin(t),0.5sin(t),0.5sin(t)]，单位为m/s2。

仿真结果如图4～8所示。图4、图5、图8中实线代表位置通道带有干扰且虚拟平面内也存在干扰，利用本文提出的抗干扰视觉伺服控制进行的实验；虚线代表存在干扰但是没有抗干扰的视觉伺服控制的实验。图6实线代表线速度实际值，虚线代表线速度估计值。

图4(a)是四旋翼的位置变化，表明本文提出的控制器能够有效地抑制位置通道上的干扰。图4(b)是四旋翼的姿态变化，表明该控制器能够在存在干扰的情况下得到更好的姿态变化。

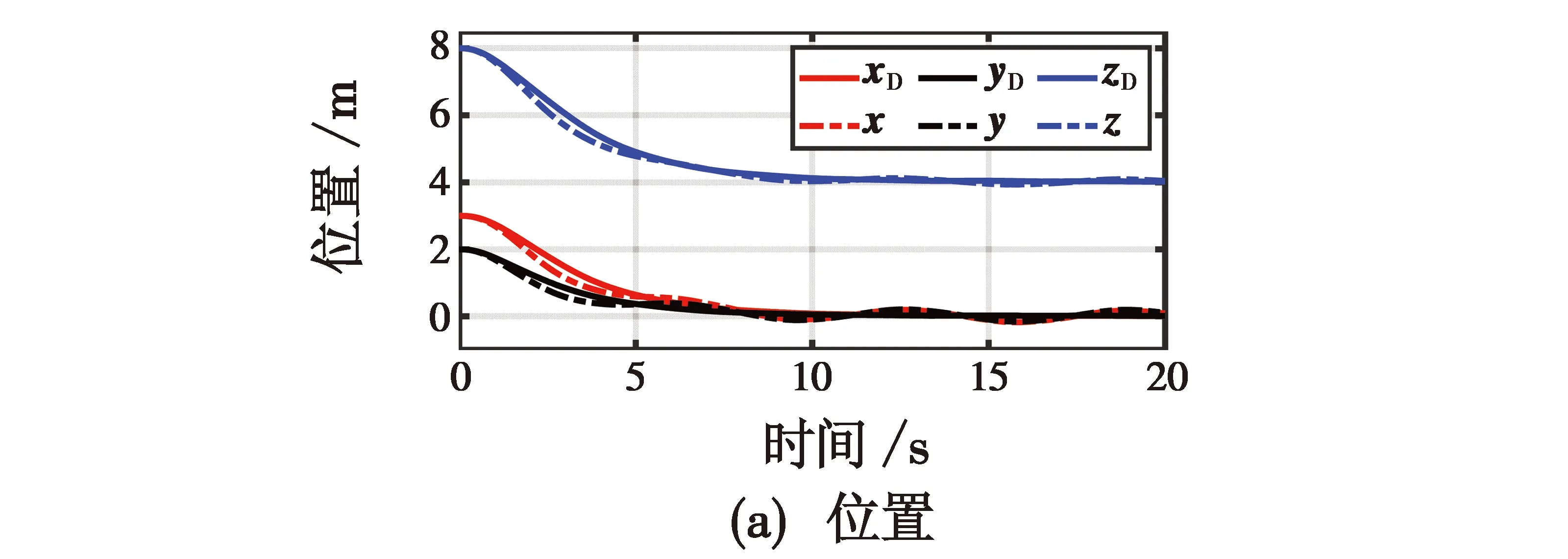
图4 四旋翼无人机位置与姿态

图5结果表明,通过本文控制器能够有效地使误差收敛，并且更稳定。图6结果表明,通过抗干扰视觉伺服控制不仅能够在虚拟平面内有效地抑制干扰，在真实平面内的干扰也能有效抑制，得到光滑的线速度轨迹。图7表明本文控制器能够有效地抵抗干扰，且生成稳定的特征轨迹(虚线为真实图像平面，实线为虚拟平面)。图8是四旋翼的控制输入，通过该抗干扰控制器能够相对稳定地控制。无论是否存在干扰，本文提出的视觉伺服控制器均能实现对四旋翼进行鲁棒控制，是合理和有效的。

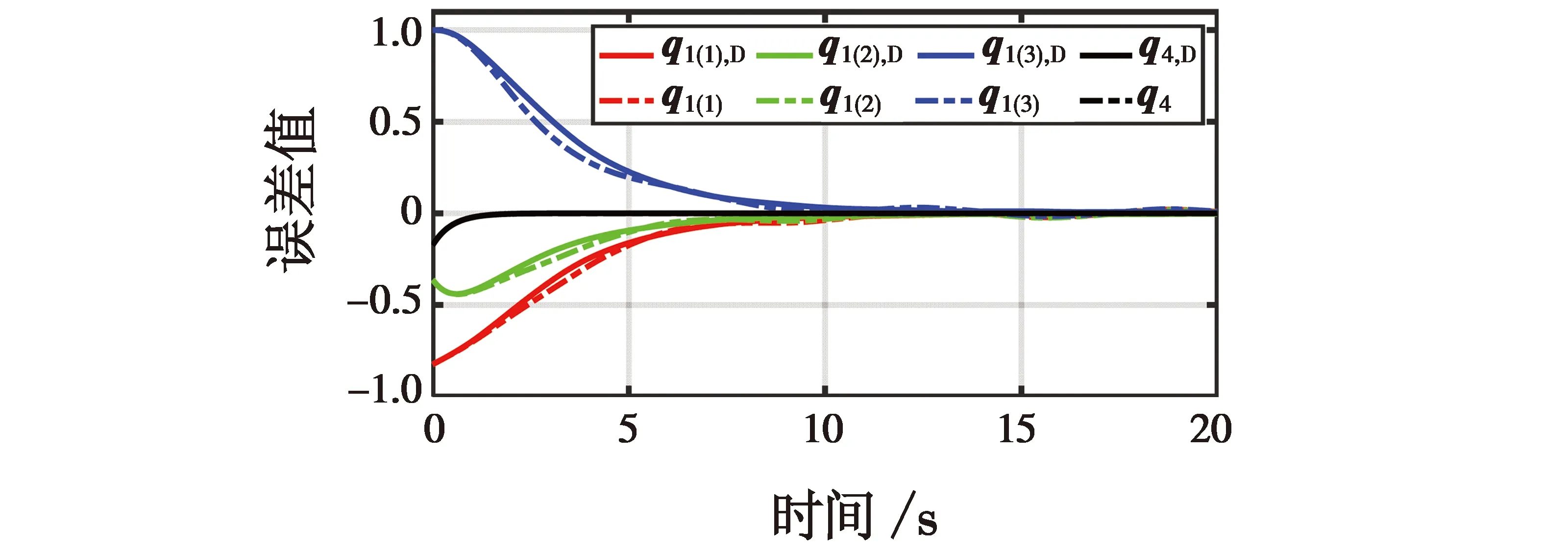
图5 特征误差

图6 四旋翼无人机线速度

图7 特征轨迹

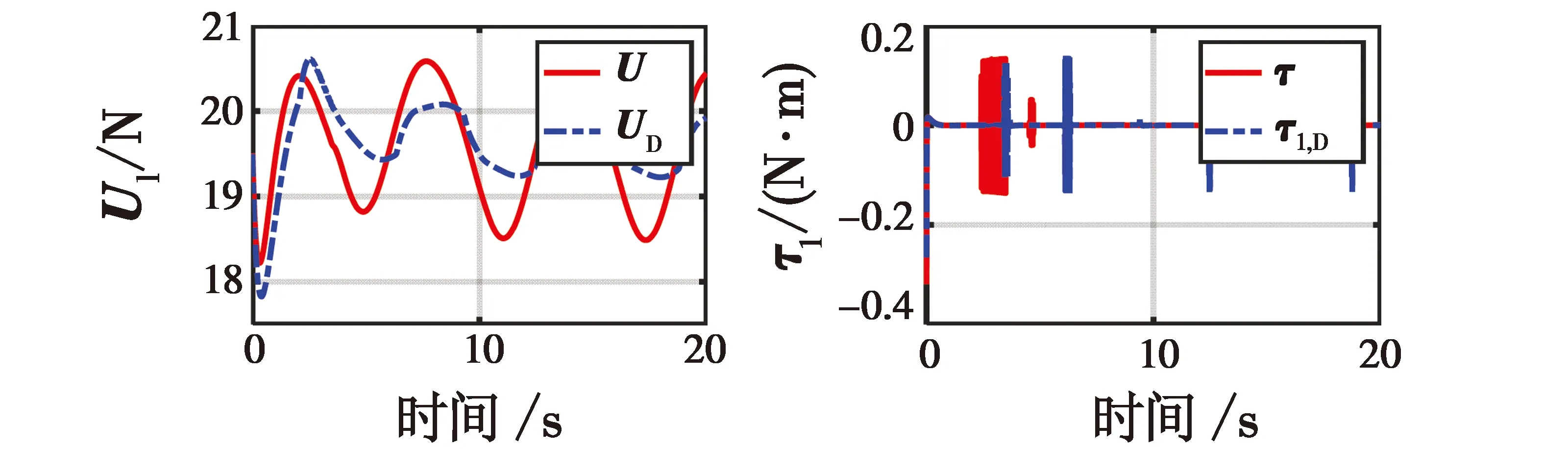
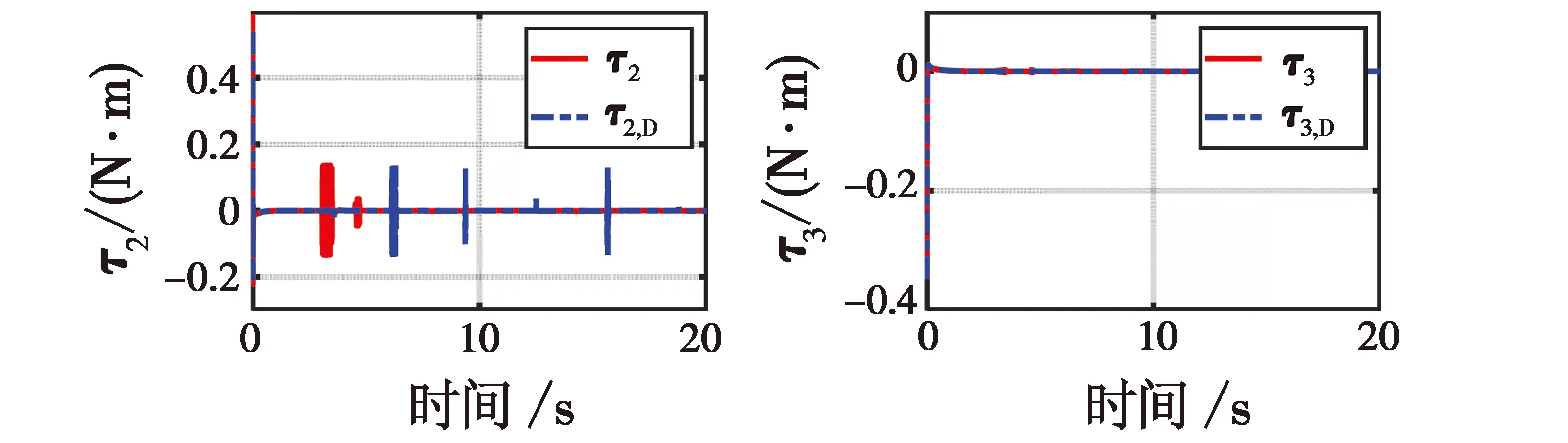
图8 四旋翼无人机控制输入

5 结束语

本文对四旋翼无人机在存在内外部干扰的情况下的视觉伺服问题进行了研究，提出了一种基于图像的抗干扰的视觉伺服控制方法。通过虚拟平面和图像矩特征对系统进行解耦。针对线速度难以直接测量的问题，设计了速度估计器，对特征误差设计了估计器。通过Lyapunov理论证明了控制器的稳定性，利用仿真实验验证了本文方法具有良好的抗干扰的视觉伺服性能，具有较强的鲁棒性，稳态误差更小、更稳定。