信息技术在初中数学教学中的融合应用
——以几何画板辅助数学教学为例
2023-03-11海南省三亚市第一中学刘斯殷
◎ 海南省三亚市第一中学 刘斯殷
数学老师常常会听学生说:“一学数学就脑壳疼。”科学研究证明,在思考数学问题而感到苦恼时,大脑的活动区域与感受针刺等身体疼痛的大脑区域在空间上有一定的重叠,所以说“一学数学就脑壳疼”这句话在一定程度上是有科学依据的,学数学确实会让一部分人感到“脑壳疼”。究其原因,数学本身是一门抽象的语言,以贯穿了中小学的鸡兔同笼问题为例,为什么看着兔子数它们的腿容易,看着书上的题目计算就那么让人难以理解,这是因为数兔子腿时调动的是形象思维,而计算时我们处理的是非常抽象的数量关系,需要一定的抽象思维能力。
数学的研究对象是抽象的,学习过程也是一种抽象问题形象化、具体化的过程。在教育信息化深入课堂的今天,我们可以借助很多信息技术手段将令人“脑壳疼”的数学抽象问题形象化,再结合代数计算和解析方法让数学问题不再“令人头疼”。接下来笔者将以在初中数学教学中经常使用的一种信息技术手段“几何画板”为例,具体分析在教学中应如何将几何法、代数法和解析法相结合来解决几何问题、代几综合问题。
一、“数学实验”培养几何思维
几何知识的学习在初中数学中占有很重要的地位,然而几何问题的逻辑性和几何图案的抽象性却让很多学生望而却步。就笔者所在学校学生的数学基础而言,普通的九年级班级中仅有不到10%的学生能够独立解决较复杂的几何综合问题,30%以内的学生能够独立解决中等难度的几何综合问题。
初中数学的几何教学知识结构具有很强的系统性,在接触最基础的几何知识过程中让学生参与到几何图形的构建中来,能够激发他们的学习兴趣。
以“平行线的三线八角”教学内容为例,教师可以使用几何画板再现知识发现的过程。在几何画板的操作界面里,让学生自行在三线的动态变化过程中找到何时会出现同位角相等、内错角相等情况,通过发现知识、自主归纳等来培养学生的创造力。学生在这一过程中自主形成了知识框架,这样的教学过程更能够达成数学教学的核心素养,培养学生的学习兴趣和数学思维。
在学习“勾股定理”验证直角三角形两直角边的平方和等于斜边的平方(即a2+b2=c2)时,教师可以先让学生动手实践画出直角三角形,并进行测量验证,但在测量的过程中可能会出现误差,导致验证不成功。而放在几何画板中,通过动态演示并进行度量,学生会直观地发现它们之间的关系,从而体会数学与信息技术之间的联系。
在其他几何知识的学习中同样可以让学生动手操作,自己寻找解决问题的方法。例如在解决几何综合问题时,教师可引导学生通过分解步骤来寻求多种解法,开阔学生的解题思路,让学生通过几何画板作图,对图形进行分析,寻找解题的多种可能性。
学生通过几何画板的操作自主寻找解题思路的过程,如同在课堂上给学生提供了一个数学实验的环境,较之普通课堂更能够提高学生的学习兴趣,培养学生的数学思维,有助于提高学生的解题能力。
二、数形结合的解题思想
代几综合问题是初中中考必考的考点,也是初中阶段的难点问题。讲解此类问题时,可以借助几何画板先对题目进行几何分析,再结合代数法、解析法来解决问题,采用数形结合的解题思想既能让学生对题目的几何动态变化有更直观的理解,也能够实现不错解、不漏解的目标。以代几综合问题中的“等腰三角形存在性问题”为例,解决此类问题时,可以采用“两圆一线法”。两圆一线法的原理为:根据等腰三角形的定义,根据两腰的三种情况进行分类讨论,解题方法可采用几何法、代数法、解析法。
例题:在平面直角坐标系中,抛物线y=-x2+2x+3交x轴于点A(-1,0),交y轴于点C(0,3),抛物线的对称轴交x轴于点D(1,0)。在x轴上是否存在点P,使得△PDC为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
在此题中,当分别以P、D、C为顶点时,会产生多个等腰三角形,传统的纸笔作图法做几何分析题出现漏解的几率比较大。使用几何画板展示,先给出主要的解题思路,再分步骤给出三种情况下的几何图形及代数解法、解析解法,可以让学生对该类问题的解题思想有更透彻的理解。
首先用几何画板给出解题思想,当以点C为顶点,CD=CP时,以点C为圆心,CD长为半径画圆,此圆交x轴于一点,此时为等腰三角形;当以点D为顶点,DC=DP时,以点D为圆心,CD长为半径画圆,此圆交x轴于两点,此时为等腰三角形,从几何画板中我们可以看到出现的等腰三角形会有两种情况,通过几何画板的演示,可防止漏解;以点P为顶点时,因为很难直接在x轴上找到可以令PC=PD的点P,所以可以考虑做线段CD的中垂线,与x轴相交,交点即为所求点P,为等腰三角形。
几何画板演示如图1、图2、图3:
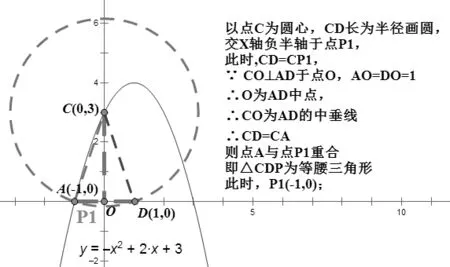
图1
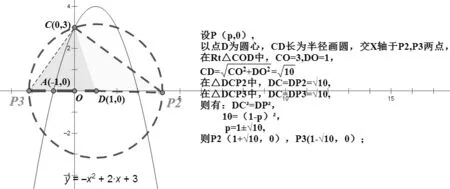
图2
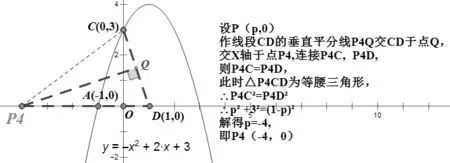
图3
“一线”法的解题过程也可以使用解析法,将二次函数解析式和CD中垂线的解析式联立来解题,具体过程不再赘述。
最后对以上等腰三角形存在的多种情况做综述,再作此类型题的解题方法总结。通过以上操作,借助几何画板的几何分析,配以代数法、解析法的解题过程,能够让学生深刻理解复杂的代几综合问题。
除几何画板以外,微课也是数学教学中一种不错的信息技术手段。针对目前“双减”政策中提出的多样性作业设计,可以给学生布置数学知识微课作业并进行展评。数学微课的制作在提高学生数学兴趣的同时还可以巩固知识、培养学生学习的积极性,提高学生的信息技术素养。
电脑阅卷后的精准数据分析有利于教师把握学情,学生课堂练习后的同屏展示等有助于让学生了解更多的解题思路。
总之,信息技术在课堂教学中的应用,停留于视觉吸引是非常具有局限性的,应以培养学生的核心素养为目标,调整教学方法和策略,充分发挥其视听结合、手眼并用的特点及其模拟、反馈、个别指导的内在感染力,使用信息技术工具抓准课堂教学中的问题关键,提高学生学习数学的内驱力。
