小画板，大妙用

◎ 福建省南安市诗山中学 洪丽云

几何画板是一种常用的数学、物理教学软件，是信息技术与数学教育教学融合的主要媒介，其精准作图和动态变换的功能给学习者提供了无尽的创造思维。本文基于初中数学学科特性,分析几何画板软件的特点与优势,结合初中数学教学实践,通过制作几何画板动态课件,辅助初中数学课堂教学,激发学生学习兴趣,进而提高课堂效率。

一、动感实验，妙在探究

信息技术为数学教学的变革提供了新的方式。数学实验教学是再现数学发现过程的有效途径,是一种活动性教学,它能满足不同学生的需求并使学生得到不同程度的发展。借助几何画板进行数学动感实验,探究正多边形铺设地面的实践,可培养学生的探索精神,提升学生的核心素养。

教师提前做好正多边形工具,在课堂上教学生如何使用工具,然后让学生利用电脑进行操作,操作时分同种正多边形、两种正多边形和三种正多边形,操作前渗透分类讨论思想,教会学生有规律地进行问题探究。通过直观观察，学生发现用相同的正多边形铺设地面时，只有正三角形、正方形、正六边形可以铺满地面，而正五边形不能铺满地面。教师此时引导学生观察铺满地面的图形的条件，通过观察，部分学生发现“当围绕一点拼在一起的几个内角加在一起恰好组成一个周角，即360°时，所用的多边形地砖就可以铺满地面”。

那么给定一个正多边形需要多少个这样的正多边形才能在一点处铺满呢？以正三角形为例，假设需要x个正三角形，那么在一点处的x个内角加起来是360°，由此得到：

这就将铺设地面问题转换为了一元一次方程正整数解模型。通过这个转换，教师布置练习，用这种数学建模思想引导学生探究正七边形、正八边形等能否在一点处铺满地面呢？学生通过探究发现，用同一种正多边形铺设地面时，只有“正三角形、正方形、正六边形”能够铺满地面，其他不行，并进一步得出结论“当正多边形的一个内角能被360°整除时，这个正多边形地砖便能铺满地面”。学生通过自己模拟体验铺设地面，将生活问题转换成了数学模型，数学建模思想就这样在体验的过程中印在了学生的脑海里。

通过运用数学建模思想,教师可引导学生探究用2种正多边形铺设地面的问题，以正三角形和正方形为例，设有x个正三角形，y个正方形，则：

2种多边形的铺设问题就转化成了二元一次方程的正整数解问题，当学生得到了正确结果时，教师还可进一步引导学生通过画板来验证猜想结论的正确性。

当用三种多边形铺设地面时，以x个正三角形，y个正方形，z个正六边形为例，则：

这就转化成了三元一次方程正整数解问题。

通过几何画板动态演示实践操作体验、模型总结、模型运用、操作验证，将学生的课堂积极性调动起来，不仅能活跃课堂氛围，同时还渗透了数学思想、解题方法的教学。

二、动静结合，妙在理解

几何画板软件是集静态精准作图和动态变换探究功能于一体的数学作图软件,用户根据自己的理解运用创作出丰富多彩的课件,动静结合,直观展示,帮助学生理解数学知识,感悟数学思想,破解教学重难点。例如探究二次函数一般式的系数对函数图像的影响时,教师可通过制作好的课件让学生动手体验,如改变a、b、c的数值,观察函数图像发生的变化,猜想二次函数系数a、b、c对图像的影响,从而总结规律:依次改变a、b、c时,函数图像的开口方向、开口大小、对称轴、与y轴交点位置发生变化,直观形象地呈现出“形变数就变,数变形也变”的互相依存关系,学生自然而然体会到数形结合的妙处,培养了学生几何直观和数形结合的思想。

在“一次函数性质”教学中,学生对“一次函数的系数k、b的改变对一次函数图像的影响”理解存在问题,利用几何画板度量点的坐标功能,得到度量值k、b,再利用热文本功能,将度量值k、b关联入解析式,通过上下拖动点k、b,改变系数,引导学生观察图像变化趋势及所在象限,得出结论：当|k|增大时,直线倾斜度增加,与x轴夹角增大,当|k|减小时,直线倾斜度减少,与x轴夹角变小,为后续的学习打下基础;当b＞0时,图像向上平移b个单位,当b＜0时,图像向下平移|b|个单位,渗透平移的几何变换思想;当k＞0,b＞0时,图像过一、二、三象限，当k＞0,b＜0时,图像过一、三、四象限，当k＜0,b＞0时,图像过一、二、四象限，当k＜0,b＜0时,图象过二、三、四象限。通过动态变换,让学生体会运动变换的思维,培养数形结合思想,渗透用数学的眼光观察现实世界和用数学的语言表达现实世界的核心素养。有了以上探究经历,通过融汇贯通类比思想,学生在探究反比例函数图像与性质时就会容易许多。

三、几何变换，妙在构图

不规则图形阴影面积的计算在中考中屡见不鲜,学生解决此类问题的方法和破题点往往有失偏颇,但如果我们在教学中渗透几何变换法,将部分图形进行平移、旋转、翻折等变换,从而将不规则图形转化为规则图形,将分散图形集中,那么这类问题就会迎刃而解,而此中破解之道就在于“如何进行几何变换”和“为什么会想到这样的变换方式”。

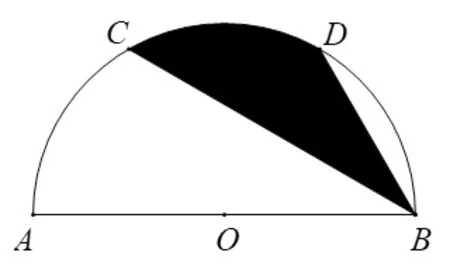
图1

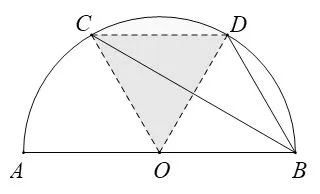
图2

分析：图中阴影为不规则阴影,无法直接运用已知的图形面积公式计算,通过对阴影图形分析,连结CD,阴影部分被分割成弓形和三角形,由已知条件易证CD//AB,利用平行线间的距离处处相等可得S△BCD＝S△OCD。因此将不规则阴影图形面积转化为弓形和正三角形的面积和,即扇形,进而求解。

例2：如 图3，在△ABC中，CA＝CB，∠ACB＝90°，AB＝2，点D为AB的中点，以点D为圆心作圆心角为90°的扇形DEF，点C恰在弧EF上，则图中阴影部分的面积为________。

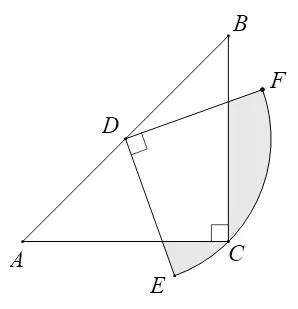
图3

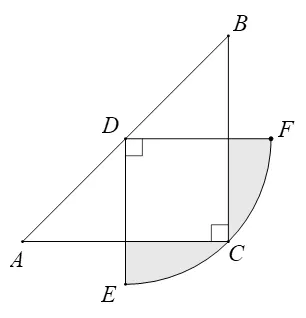
图4

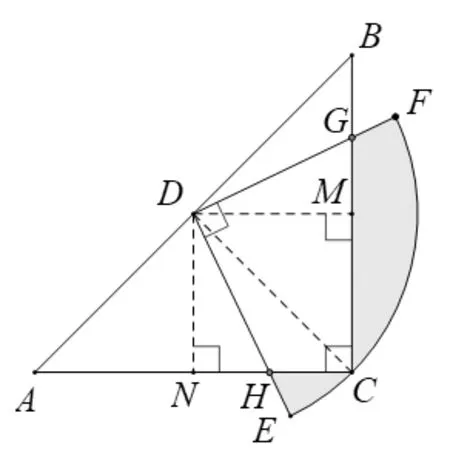
图5

求解不规则图形面积时,通过对不规则图形进行分析,添加适当的辅助线,将图形进行分割转化,再将分割后的图形进行几何变换,实现将不规则图形转化为规则图形、将部分转化为整体的效果,从而利用规则图形面积公式进行计算求解。

四、动态定位，妙在分类

中考压轴题的核心是数形结合,数形结合的精髓是函数,函数的核心是运动变化。图形的运动变换,归根结底是图形上点的运动变换。图形的动态型问题由于具有运动对象的多样性、运动路径的多变性、运动条件的制约性、运动结果的丰富性,更兼具涉及数学知识的综合与核心、考查形式新颖等特点而备受中考命题者的青睐。这类问题一般设计为探究性问题和说理与计算推理相结合这两类综合题，具有以下特点：试题所给的图形只是运动元素(对象)在整个运动过程中的其中一种情况反映,整个运动过程中会出现多种情形,其中另外几种情形都需要学生在较短的考试时间内自主探索、通过画图寻找。由于考试时间紧张、思维坡度大,同时需要考虑不同时段、不同条件下的图形运动情形,许多学生对此感到恐惧、茫然,不知从何处入手来应对,这对学生来说是一种挑战。而利用几何画板动态演示功能进行动态定位分析和画静态分类示意图两步策略,能帮助学生有效解决这类动态变化型问题。

所谓动态定位分析,就是着眼于问题全局,先从整体层面上分析动点的运动路径与运动区域,初步获得并做好先期性解题规划。而据此所画出的静态分类示意图,就是根据动态定位分析中每一种运动类型下运动元素的运动情况,画出该元素所满足要求的运动趋势下的静态图。解题思考过程重点考查学生对运动过程的分析,突出数形结合思想及分类讨论思想，以下题为例。

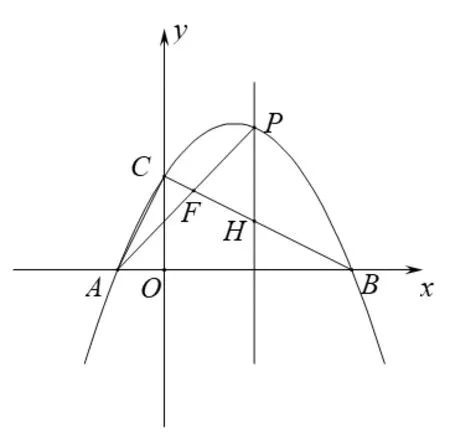
图6

(1)(2)略；

(3)若点P在第一象限,直线AP交BC于点F,过点P作x轴的垂线交BC于点H,当△PFH为等腰三角形时,求线段PH的长。

动态定位分析：点P在第一象限运动过程中,△PFH的形状发生变化,存在某些时刻,使得△PFH为等腰三角形,但等腰△PFH的哪两边相等不确定,根据等腰三角形两边相等进行分类,具体有PF=PH、PF=FH、PH=FH三种情况。

静态分类分析：根据PF=PH、PF=FH、PH=FH三种情况画出分类示意图如图7、图8、图9所示。

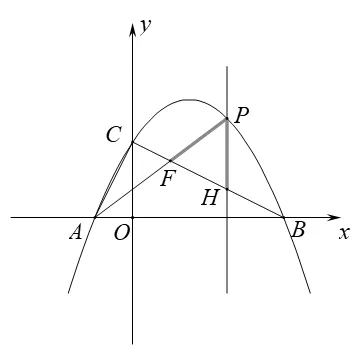
图7

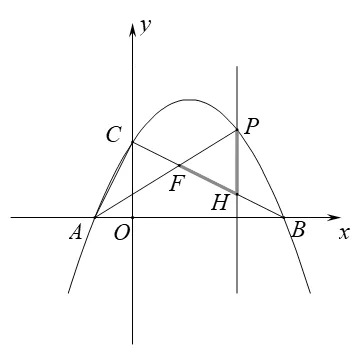
图8 图9

破解策略分析：本题为等腰三角形的存在性问题,根据等腰三角形定义两边相等进行分类讨论,解题视角不同,解题方法也会不同,而借助几何图形的特征求解可以有效降低运算量。

小画板,大妙用。几何画板辅助课堂教学并不仅限于此,课程标准多次强调信息技术与教育教学融合的必要性,同时也强调数学软件辅助课堂教学的趋势,而几何画板正是辅助初中数学课堂教学的有力工具,教师应通过长期实践,不断反思,争取让小画板发挥更大的妙用,助力数学课堂改革,减轻学生学习负担,提高学生学习质量。