基于压痕测试技术的聚乙烯老化力学性能评价

代星辰，黄奕昶，关凯书

(1.华东理工大学机械与动力工程学院，承压系统与安全教育部重点实验室，上海 200237；2.上海市特种设备监督检验研究院，上海 200333)

0 引 言

聚乙烯(PE)具有优异的耐冲击性、抗震性和耐腐蚀性，常用作高压燃气管道材料[1-2];与普通钢管相比，聚乙烯管易加工、耐腐蚀且成本低[3-4]。聚乙烯在热氧、紫外线等环境下长期使用时，容易发生高分子链断裂或者抗氧剂失效导致的材料老化现象，造成材料的综合力学性能下降，导致燃气泄漏，影响管道的安全使用。力学性能的变化是评价高分子材料老化的一个重要方法，通常采用缺口冲击强度、弯曲强度、最大断裂载荷以及拉伸强度等力学性能对聚乙烯材料的老化程度进行表征[5-8]，但通常这些常规检测的取样难度较大、成本高且耗时长。压痕测试作为一种微试样测试技术，具有取样小、时间短且操作简便的优点，该技术常用来测试金属材料的力学性能，如评估316L奥氏体不锈钢和16Mn钢的拉伸性能[9-10]、叶轮常用钢的力学性能[11]等，很少应用于高分子材料的力学性能表征。若能通过机加工方式从聚乙烯管道截取微试样进行压痕试验，获取材料的力学性能以评估管道的老化程度，不仅能够减少常规测试对管材的损耗，还能降低取样难度，缩短测试时间，减少测试成本。因此，作者以85 ℃老化不同时间的聚乙烯试样为研究对象，通过改变压痕试验的加载速率[12-15]以减少材料黏弹性的影响来获取材料趋于理想弹塑性响应的压入速度，在该加载速率下进行压痕试验得到不同老化时间下聚乙烯试样的最大载荷，通过有限元数值模拟建立屈服强度与最大载荷的线性关系，计算材料老化后的屈服强度，并与拉伸试验结果进行对比，验证压痕测试技术评估聚乙烯力学性能的准确性。

1 试样制备与试验方法

试验材料为橙色PE100 SDR11燃气管，市售，执行标准为GB/T 15558.1-2015，密度为0.959 g·cm-3，管外径为160 mm，壁厚为14.6 mm，在190 ℃下熔体质量流动速率为5 kg/10 min。按照GB/T 714-2008，选用热氧老化方式对截取的部分聚乙烯管进行人工加速老化处理，试验装置为强制通风式热老化试验箱，箱内持续通风，温度保持在85 ℃，老化时间分别为0，168，312，408 h。

按照GB/T 8804.3-2003，在老化后的聚乙烯管上加工出如图1所示的拉伸试样，取样时试样的纵向平行于管材的轴向，标距段截面尺寸为10 mm×10 mm，标距长度为50 mm，采用RGM-4050型万能材料试验机进行室温拉伸试验，拉伸速度为50 mm·min-1;对不同时间老化的聚乙烯试样分别进行3次拉伸试验，取平均值。在老化后的聚乙烯管上平行于管材的轴向加工出尺寸为30 mm×10 mm×5 mm的压痕试样，用2000#砂纸将试样上、下表面打磨光滑后，采用自制的仪器化压痕试验机进行压痕试验，该试验机由伺服电机、驱动结构、力传感器、位移传感器、一体化压头结构等部件构成。试验选用直径5 mm的一体化碳化钨球形压头；位移传感器固定在压头尾部，以减少机架柔度对试验结果的影响，测试精度为0.1 μm。在压痕试验过程中，通过伺服电机驱动球形压头压入待测试样表面，由位移、力传感器记录试验过程中的位移和载荷数据。为减少聚乙烯材料本身黏性的影响，在0.01，0.04，0.06，0.1，0.2，0.3，0.4，0.5，0.6，0.7 mm·min-1的压入速度以及400 N最大压入载荷条件下，对未老化试样(老化时间0)进行压痕试验，确定使材料趋于理想弹塑性响应的加载速率。在固定压入速度下，对不同老化时间的聚乙烯试样进行压入深度为0.45 mm的压痕试验，获取不同老化时间下聚乙烯材料的载荷-位移曲线。

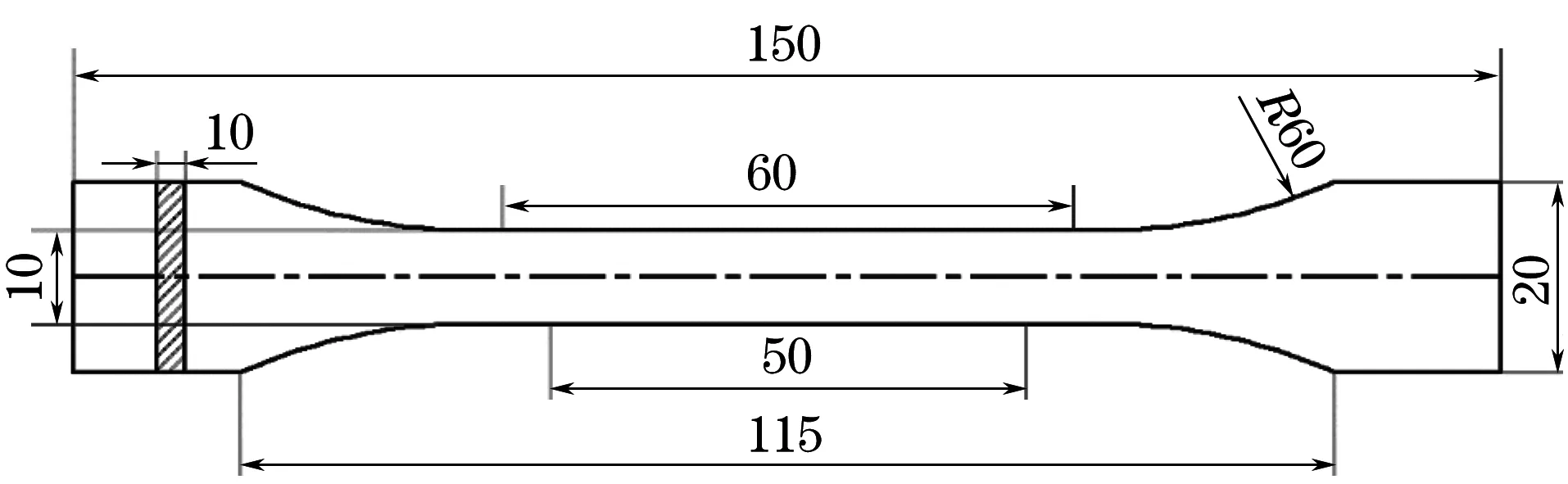
图1 拉伸试样的尺寸

2 结果与讨论

2.1 拉伸应力-应变曲线

由图2可以看出，随着老化时间的延长，聚乙烯试样的屈服强度和断裂时最大载荷逐渐增加，断后伸长率逐渐降低。

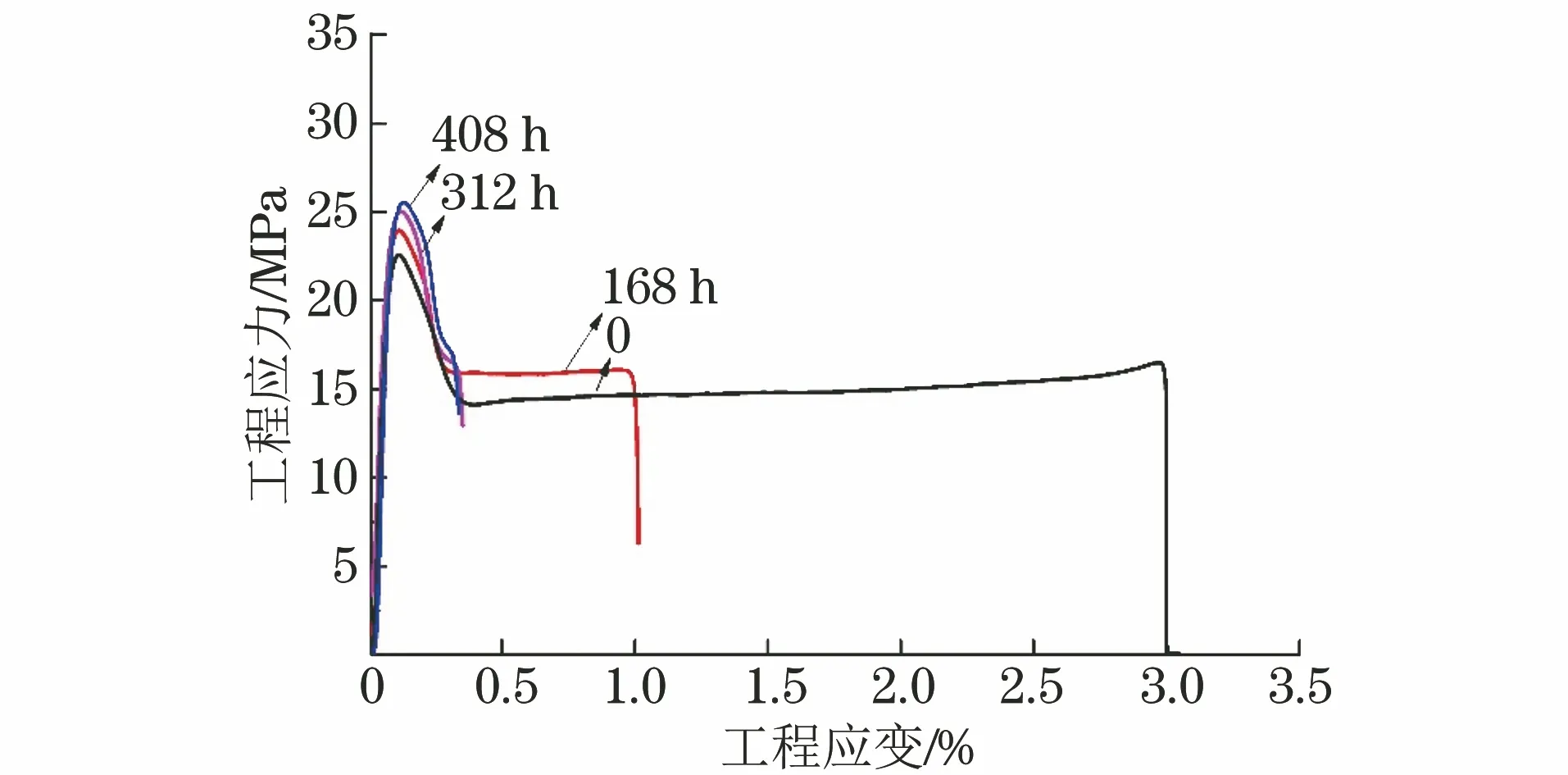
图2 不同老化时间聚乙烯试样的拉伸工程应力-应变曲线

2.2 压痕载荷-位移曲线

由图3可以看出，随着压入速度的增加，未老化聚乙烯试样的载荷-位移曲线左移，当压入速度接近0.7 mm·min-1时，载荷-位移曲线基本不再随着压入速度变化而改变。这说明随着压入速度的增加，聚乙烯的黏性变形先逐渐减小后基本不变。可知，当压入速度为0.7 mm·min-1时，聚乙烯的载荷-位移响应趋于理想弹塑性状态。

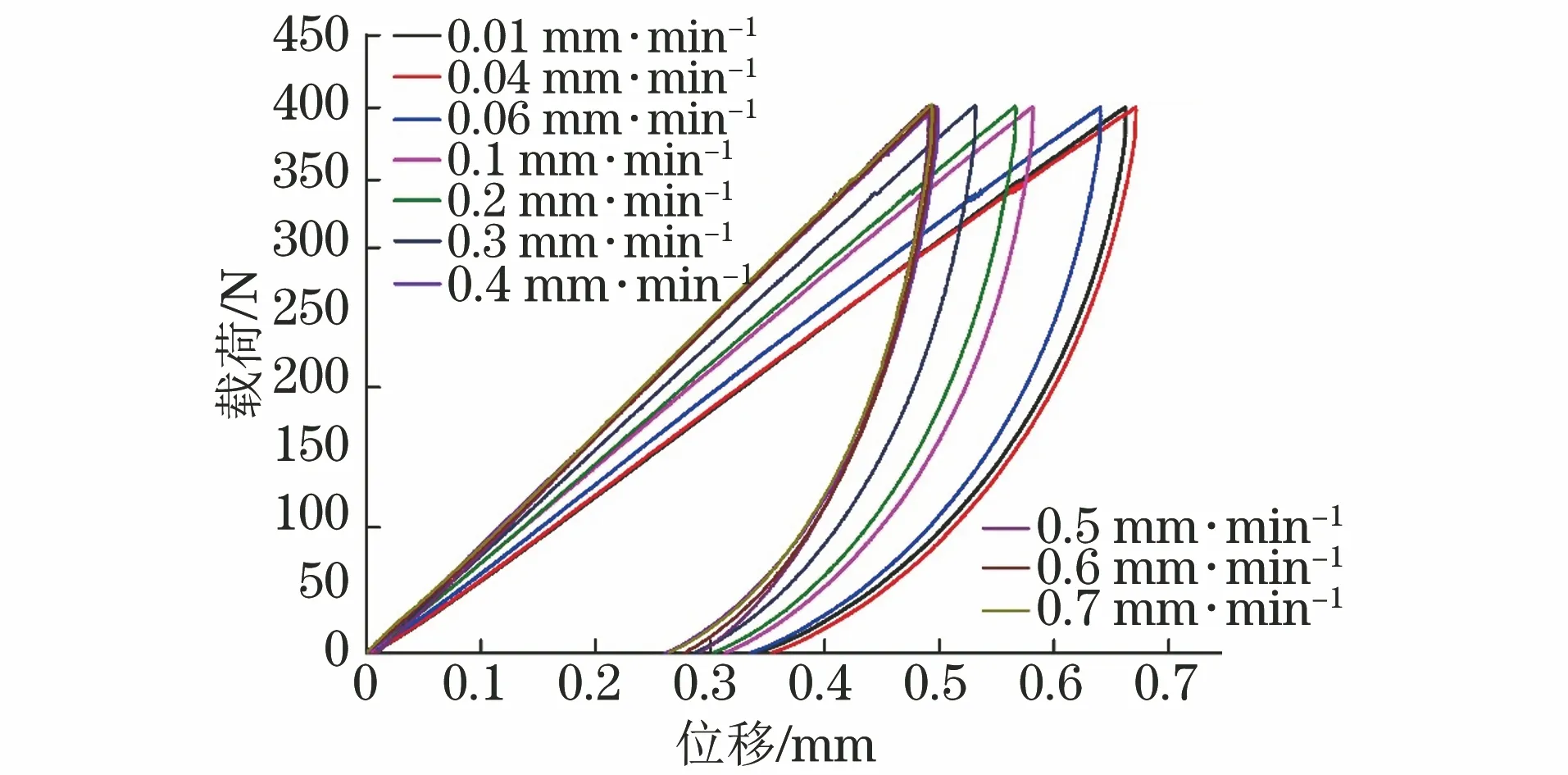
图3 不同压入速度下未老化聚乙烯试样的压痕载荷-位移曲线

由图4可知，在0.7 mm·min-1压入速度和相同压入深度下，随着老化时间的延长，聚乙烯试样的最大压入载荷逐渐增加。可知，随着老化时间的延长，压痕试验的最大载荷与拉伸试验中的屈服强度都逐渐增加。

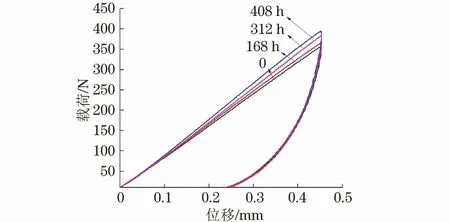
图4 0.7 mm·min-1压入速度下不同老化时间聚乙烯试样的压痕载荷-位移曲线

2.3 屈服强度的有限元模拟和试验验证

2.3.1 有限元模拟

为了建立压痕试验的最大载荷与拉伸试验的屈服强度的关系，采用有限元分析软件Abaqus对不同老化时间聚乙烯试样的压痕试验进行有限元模拟。压头直径为5 mm，将压头设为解析刚体。压痕试样尺寸为30 mm×10 mm×5 mm，为轴对称结构，建立二维轴对称模型，以提高计算效率[14]。采用4节点轴对称缩减积分单元(CAX4R)划分网格，并对压头和试样接触区域进行网格细化，最小网格尺寸为0.001，具体的网格划分如图5所示，压头与试样之间的摩擦因数设定为0.2[16]。边界条件与试验一致，在试样底部施加竖直方向的约束对试样进行固定，压头固定压入深度为0.45 mm，压入速度为0.7 mm·min-1。聚乙烯材料模型为理想弹塑性模型，弹性模量为1 500 MPa，泊松比为0.41，密度为0.959 g·cm-3[17]。

图5 压痕试验的有限元模型网格划分示意

由图6可知，聚乙烯试样的塑性应变区域近似球冠形，且随着压入深度的增加，塑性应变区半径逐渐增加至定值。

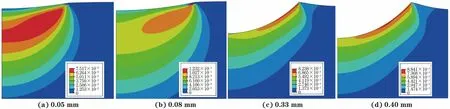
图6 模拟得到不同压入深度下聚乙烯试样的塑性应变云图

2.3.2 最大载荷与屈服强度的关系

基于JOHSON[18]提出的膨胀孔洞模型推导屈服强度，该模型按照应力状态将试样的变形大致分成核心区、塑性区和弹性区。为简化分析过程，将核心区合并到塑性区[19]，如图7所示，此时弹塑性边界视为半径为rp的球形。

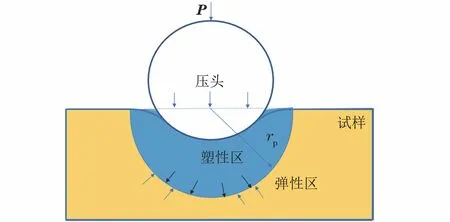
图7 压痕试验时的简化膨胀孔洞模型示意

根据膨胀孔洞理论，材料在弹塑性边界上受到均匀分布的径向应力σrr，与材料的屈服应力σy关系[18]可表示为

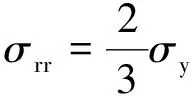
(1)

考虑竖直方向的受力平衡，压入载荷P与径向应力竖直方向的分量在整个弹塑性边界上的积分相等，参考文献[19]可以得到压入载荷、屈服强度和塑性区半径的关系：

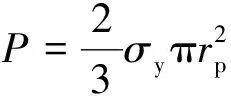
(2)

由式(2)可知，材料的屈服强度和最大载荷存在一定的关系。对屈服强度为18，20，22，24，26 MPa的5种不同聚乙烯试样的压痕过程进行模拟，获取对应的最大载荷，建立最大载荷与屈服强度之间的关系。由图8可知，压痕试验的最大载荷与材料的屈服强度近似为线性关系，此时材料的塑性区半径为定值，斜率K为13.964，线性相关系数R2为0.995，拟合公式为

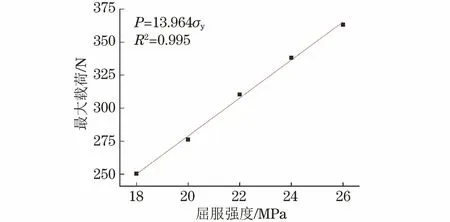
图8 模拟得到聚乙烯试样的最大载荷与屈服强度的拟合曲线

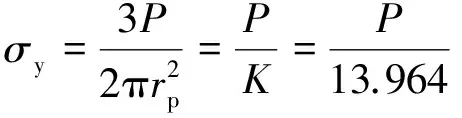
(3)

2.3.3 试验验证

将基于压痕试验获取的最大载荷计算得到的屈服强度与拉伸试验得到的屈服强度进行对比。由表1可以看出：基于压痕试验获取的最大载荷计算得到的屈服强度与拉伸试验结果之间的相对误差小于1.5%，说明压痕测试技术能够较准确地获取聚乙烯材料的屈服强度。

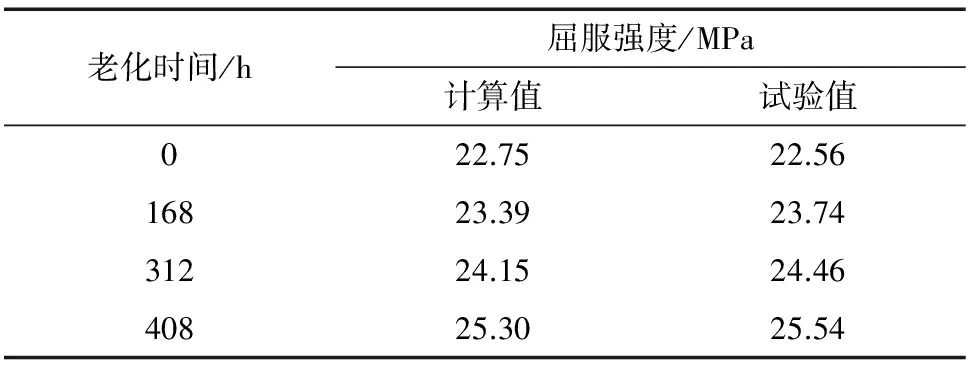
表1 由压痕试验获取的最大载荷计算得到不同老化时间聚乙烯试样的屈服强度和由拉伸试验得到的屈服强度的对比

3 结 论

(1)随着老化时间的延长，拉伸试验得到聚乙烯试样的屈服强度逐渐增加，压痕试验得到最大载荷也逐渐增加。

(2)通过有限元方法建立的聚乙烯试样压痕试验最大载荷和屈服强度的线性相关系数为0.995，基于压痕试验获取的最大载荷计算得到的不同老化时间聚乙烯试样屈服强度与拉伸试验结果之间的相对误差小于1.5%，说明压痕测试技术能够较准确地获取老化后聚乙烯材料的屈服强度。