基于稠密连接网络的地下水污染替代模型研究

2023-03-10江思珉孔维铭吴延浩刘金炳张春秋夏学敏

同济大学学报（自然科学版） 2023年2期

江思珉，孔维铭，吴延浩，刘金炳，张春秋，夏学敏

（1.同济大学土木工程学院，上海 200092；2.长江生态环保集团有限公司，江苏南京 210019；3.上海理工大学环境与建筑学院，上海 200093）

地下水系统一旦受到污染则很难恢复，并将长期影响地下水水质、地下水系统生态平衡和人体健康。与地表水相比，地下水一旦遭受污染其治理和修复难度更大，往往需要更长的时间（常常持续 30年以上），费用非常昂贵［1］。通常来说，要对地下水进行有效的治理和修复，需要大致弄清污染源信息（地下水污染溯源）以及能够对含水层性质（渗透系数等）进行准确表征（模拟参数反演），这是地下水数值模拟领域亟待解决的重要逆问题。地下水污染溯源和渗透系数场参数反演问题等除了逆问题具有不适定性的挑战，还面临计算负荷量的制约［2］。为降低地下水反演问题的计算成本，已有研究考虑提出效率更高的反问题求解算法［3］、采用性能更高的计算设备进行并行计算等［4］。作为另一种可行的解决方法，替代模型方法在近年受到越来越多的关注。

替代模型依据其构建方式一般可分为两大类，第一类是数据驱动的模型［5-6］，第二类是过程简化的模型［7-8］。但是，当前的应用主要集中于相对低维的问题，在刻画高维问题时替代模型方法的性能和效率急剧下降［9-11］。近年来，随着计算机性能的大幅提高，尤其是图形处理器（GPU）的出现，深度神经网络凭借其优秀的鲁棒性和泛化能力成为计算机视觉、空间降维计算、替代模型等领域的热点研究方法。Zhu 等［12］提出了用无监督学习（unsupervised learning）的方法来构造替代模型。Zhu 等［13］将贝叶斯理论引入卷积神经网络（convolutional neural networks，CNN），提出了一种新的 CNN 架构—BNN（Bayesian neural network），在训练数据有限的情况能够构建出较高精度的替代模型。Peterson等［14］提出基于时间序列的地下水自回归（autoregressive，AR）替代模型，预测不同气候情景下的地下水位。Mo 等［15］针对污染源附近区域非线性浓度梯度较大的问题，提出了在网络损失函数中对污染源及邻近网络加大权重（weighted loss，WL）的自回归替代模型。

现有研究在利用各类神经网络构建地下水污染替代模型时，并未结合具体的应用场景对神经网络的函数选择、参数敏感性等进行充分考量。本文借鉴卷积神经网络的图像识别过程，考虑将地下水流运动和污染物运移问题转化为输入场图像（渗透系数场、污染源信息等）与输出场图像（水头场、浓度场等）之间函数关系的图像回归问题，通过数值算例研究稠密连接网络替代模型的有效性以及模型性能的改进策略，主要包括：针对实际应用中样本数量较少的情形提出在神经网络中采用最优正则项系数的改进策略，针对污染源附近区域存在非线性浓度梯度问题采用改进权重的网络损失函数以及神经网络激活函数的选择。

1 研究方法

地下水模拟模型是研究地下水流和污染物运移的关键，而地下水模型的输出是通过求解地下水流和溶质运移的偏微分方程获得的，这往往需要较长的计算时间。为充分刻画地下空间的异质性、考虑更多的物理过程、提高数值精确度、扩大模拟区域尺度等，都会导致计算量增大和模型运行时间的增加。单个模型运行时间的增加还会限制其在需要大量调用模拟模型的实际问题中的应用，如地下水逆问题、不确定性分析、敏感性分析等。为了提高计算效率，可以在模型中使用替代模型来替换原始模型16］。

1.1 地下水流与溶质运移模型

目前常用的污染物迁移模拟程序有MOC3D、MT3DMS、RT3D、FEMWATER、FEFLOW 等。其中，MT3DMS 是应用最为广泛的污染物迁移模拟程序。本文采用MT3DMS 程序进行地下水污染物迁移模拟，MT3DMS 本身不包括地下水流模拟程序，在模拟计算时，MT3DMS 需和MODFLOW 一起使用［17-18］。

地下水水流方程如式（1）：

式中：假定渗透系数的主轴方向与坐标轴方向一致，Kx、Ky、Kz分别为渗透系数在x、y、z方向上的分量，m·d-1；h为水头，m；W为单位时间从单位体积含水层流入或流出的水量，d-1；Ss为孔隙介质的贮水率，m-1；t为时间，d。

地下水溶质运移方程如式（2）：

式中：θ为有效孔隙度；ck为溶质组分k的浓度，g·m-3；Duw为水动力弥散系数张量，m2·d-1，u为纵向弥散方向，w为横向弥散方向；vu为含水介质中的实际水流速度，m·d-1，与Darcy流速qu的关系为vu=qu/θ；qs为单位体积含水层的源汇项流量，d-1；cks为源汇项中溶质组分k的浓度，g·m-3；∑Rn化学反应项总和，g·m-3·d。

1.2 基于DenseNet网络结构的替代模型框架

深度卷积神经网络可以有效处理高维输入-输出映射，其适用于处理具有空间结构的图像数据［19］。具体地，地下水流与溶质运移模型中输入（渗透系数等）和输出（水头场和浓度场）都具有显著空间相关性，通过图像化处理后可以利用卷积神经网络建立高维输入-输出映射，该映射关系即为替代模型。模型的输入与输出的关系表示如式（3）：

式中：H×W为模型的空间剖分网格数（对应于1.1节MODFLOW有限差分网格）；dx和dy分别表示模型输入和输出的个数。对于二维模型，输入参数包含渗透系数场、污染源信息等，输出状态量包括污染浓度场和水头场。在卷积神经网络中，将输入参数和输出状态量以近似于图像的数据结构表示（高维图像），通过网络训练建立输入场图像与输出场图像之间函数关系的图像回归问题。

在图像回归问题中，全卷积神经网络是用编码网络（encoder）对高维输入图像进行特征提取，然后在解码网络（decoder）根据特征重建输出图像。随着设计越来越深的网络，深刻理解“新添加的层如何提升神经网络的性能”变得至关重要。针对这一问题，He 等［20］提出的残差网络（ResNet）在一定程度上避免深度网络的梯度消失、梯度爆炸问题和网络退化问题。稠密连接网络（DenseNet）在某种程度上可以看成是 ResNet 的逻辑扩展，它采用一种密集连接结构将不相邻层进行连接，从而减少网络传输过程的信息损失，同时避免深度增加引起的网络参数爆炸［21］。

DenseNet 由稠密块（dense block）与过渡层（transition layer）2个重要部分组成。具体地，稠密块的层与层之间的信息传递关系表示如式（4）：

式中：[x0，x1，...，xl−1]表示0 到l−1 层的输出特征图的串联操作；Hl（·）包括批归一化（batch normalization，BN）、ReLU 激活函数和卷积操作（convolution，Conv）的顺序组合等。稠密块主要由2个参数决定：结构内的网络层数L和每一层的输出特征面数量K′。通过整个稠密块的特征图数量为N0+L×K′，其中N0为输入特征图的数量。图1为稠密块结构示意图。

图1 DenseNet的稠密块结构示意［20］Fig.1 Dense block structure of DenseNet [20]

图2为图像回归问题的DenseNet网络结构示意图，其中第1层为初始卷积层，随后为稠密块和过渡层（编码层和解码层）的组合。由于每个稠密块都会带来特征图数量的增加，使用过多则会过于复杂化模型，因此需要过渡层来连接2个相邻的稠密块，通过批归一化、ReLU 激活函数和1×1 卷积等组合操作减小特征图数量［21］。此外，在图像回归问题中，过渡层在编码过程中被称为编码层（encoding layer），利用卷积操作完成特征图尺寸改变的任务（downsampling），从而实现特征提取；过渡层在解码过程中被称为解码层（deconding layer），通过反卷积操作恢复特征图尺寸（upsampling）。

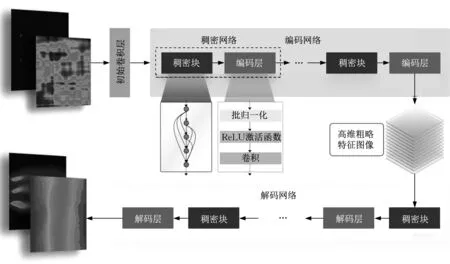
图2 图像回归问题的DenseNet网络结构示意Fig.2 DenseNet network structure for image regression problem

2 算例研究

2.1 问题概述

图3 考虑非均质各向异性承压含水层，含水层水流运动为稳定流。研究区大小为12.5m ×17.5m，离散为51×71 的均匀网格（网格尺寸为0.25 m × 0.25 m）。含水层厚度为1m。南北边界为二类隔水边界，东西边界为定水头边界，水头H分别为6 m 和5 m（图4）。场地东侧存在一口抽水井（W1，流量2 m3·d-1），降雨入渗强度为0.005 m·d-1。初始时刻，含水层中无污染物。含水介质孔隙度为0.30，纵向弥散度为1.50 m，水平横向弥散度为0.15 m。含水层渗透系数K满足对数正态分布，其均值与方差（）分别为2.0 和0.5，在x、y方向的相关长度分别为4 m 和2 m，变差函数为指数型。模拟总时长为160 d，共10 个应力期（每个应力期16 d）。

图3 含水层结构平面Fig.3 Plan view of aquifer structure

考虑到实际地下水污染问题中，根据前期场地调查往往能大致确定污染源位置，而对应污染源的释放历史是未知的。本算例中考虑3 个污染源，为S1、S2和S3。污染源参数由30个参数进行量化（3个污染源在10 个应力期的污染释放强度），即Ss=，其中i=1，2，3；j=1，2，…，10。非均质渗透系数场的反演估计通常会导致高维问题，高维参数受制于维度灾难问题，通常需要对渗透系数场进行概化和降维［22］。在本算例中，渗透系数场的维度决定于网格剖分程度（51×71=3 621），为了在可接受的计算时间内解决高维参数反演问题，采用KLE方法进行降维操作，保留前400 个KL 主要展开项（即可保留该渗透系数场近95%的非均质特征）［23］。假设表征污染源释放强度的30 个参数的先验分布是均匀分布，其先验区间和真实值见表1。

表1 污染源释放强度参数的真实值及先验区间Tab.1 True value and prior interval of release in⁃tensity parameters of pollution source

在构建替代模型前，将正演模型的输入和输出项以图像的形式表示。输入包括渗透系数场和图像化处理后的污染源参数。输出为利用原始模型（MODFLOW和MT3DMS）得到的水头和多个时刻污染物浓度场。模型输入的污染源强度（S）随时间变化，模型输出的污染物浓度除了受输入参数（渗透系数K）的影响外，还受随时间变化的污染源源强的影响。换言之，任意某一目标时刻污染物浓度场受到该目标时刻j及更早时刻（1，2，…，j−1）的污染源源强的共同影响。利用自回归模型方法，可以表示为式（5）：

式中：cj为时刻j的污染浓度场；K、S分别为当前时刻的渗透系数场和污染源参数；cj−1为上一时刻的污染分布。

考虑到地下水污染点源会对释放区域周围产生较大非线性浓度梯度，为了提高替代模型在污染源附近的预测精度，在网络损失函数中分别赋予污染源及周围8 个像素点额外权重wc（见图4）。加权损失函数表示为式（6）：

2.2 DenseNet网络结构设计

算例所用的网络结构为AR-Net-WL，即考虑式（6）定义的加权损失函数的自回归网络。AR-Net-WL 采用DenseNet 网络结构，输入样本考虑自回归策略。网络输入图片为3个，即=(K|，|Si|，|ci−1)∈R3×51×71（i=1，…，10，c0为初始浓度场），输出图片为2 个，即y=(h|，|ci)∈R2×51×71。AR-Net 和AR-Net-WL 的DenseNet 网络如表2所示，包括初始卷积层、3 个稠密块和3 个过渡层。表中，k′为卷积核大小，s为步长，p为特征图填充宽度，Wf为输出特征面数量，Nf×Hf为特征面大小，L和K ′分别为稠密块中的卷积层数和每层输出的特征面数量。其中，3个稠密块的内部层数L=［5，10，5］以增加网络深度，每一层输出的特征面为K ′=40；此外，每个过渡层包括2 个卷积层（1×1 卷积）；因此，DenseNet 网络由 27 个卷积层组成，并且不含全连接层，为全卷积网络。

表2 AR-Net-WL的网络结构Tab.2 Network structure of AR-Net-WL

在神经网络的激活函数中，sigmoid函数存在计算量大、梯度消失等局限性，ReLU 函数具有在O点处梯度不连续、在x<0时不传播等特点；softplus能够有效克服ReLU 和sigmoid 函数的上述不足之处［24］。在地下水污染问题中，输出的浓度值和水头值均大于等于零，在网络的最后一层采用 softplus激活函数，能够保证网络的浓度和水头预测值为非负数。Adam 优化算法的初始学习率设定为0.005，网络训练周期数（epoch）设定为200，若损失函数在10 个epochs 没有变化，则将学习率降至当前学习率的10%，选择L1损失函数（lasso），其正则项系数为ωd=5×10−5。

3 结果与讨论

研究DenseNet 网络（AR-Net-WL）构建得到地下水流与溶质运移替代模型的效果，分别对样本数量、DenseNet 网络超参（权重损失函数、正则项系数）等影响进行分析。AR-Net-WL 在NVIDIA GeForce RTX2080s GPU上训练。在替代模型训练时，采用决定系数（R2）和均方根误差（root-meansquare error，RMSE）评估深度卷积网络替代模型的精度。决定系数（R2）的值越大，均方根误差（RMSE）的值越小，表明替代模型的预测精度越高。

3.1 训练样本数量的影响

为讨论训练样本数量对替代模型近似精度的影响，在AR-Net-WL网络结构下考虑了4个训练样本集合，包含训练样本数量分别500、1 000、2 000和3 000。测试样本集合由Ne=500 个随机生成的测试样本组成，包括地下水稳定水位h和10 个时刻t=［16，32，48，64，80，96，112，128，144，160］d 的污染物浓度观测数据。因此，网络输入图片为3个，即=(K，|Si|，|ci−1)∈R3×51×71（i=1，…，10，c0为初始浓度场），输出图片为2 个，即y=(h|，|ci)∈R2×51×71。

图4所示为不同训练样本数量条件下训练样本和测试样本的RMSE值随训练周期数（epoch）的变化趋势。在160 个训练周期后，所有情形下的训练样本集合与测试样本集合的RMSE值都趋于稳定；完成训练周期数为200 的训练后，随着训练样本数量的增加，RMSE值呈现降低趋势，即替代模型的预测精度越高。具体地，当训练样本从1 000增至2 000时，训练集合的RMSE从0.067 6 下降到0.052 5；当训练样本从2 000增至3 000时，训练集合的RMSE从0.052 5下降到0.033 3。

图4 基于不同训练样本数量建立的替代模型的RMSE精度比较Fig.4 Comparison of RMSE accuracy of surrogate models established based on different num⁃bers of training samples

图5比较了不同训练样本数量条件下替代模型的训练样本集合和测试样本集合的R2值的变化趋势。训练样本为500 时，替代模型的训练集合与测试集合的R2值分别为0.989 2 和 0.988 1；训练样本数量增至2 000 时，训练集合与测试集合的R2值分别增加至0.997 9 和0.996 0，替代模型具有较高的精度和较强的泛化性能；随着训练样本的继续增加，测试集合与训练集合的R2值的提高幅度趋于平缓。具体地，训练样本数量从2 000 增至3 000 时，训练集合的R2值增至 0.998 7（增幅约0.08%），测试集合的R2值增至 0.998 1（增幅约 0.20%）。

图5 基于不同训练样本数量建立的替代模型的R2精度比较Fig.5 R2 accuracy comparison of surrogate models established based on different training sam⁃ple numbers

3.2 权重损失函数的影响

为了量化AR-Net-WL 网络中权重损失函数对替代模型精度的影响，分别选择AR-Net-WL和ARNet 网络构建替代模型（训练样本数量为3 000），比较训练样本和测试样本的R2与RMSE指标。由表3可知，AR-Net 和AR-Net-WL 替代模型都具有较高的精度，考虑权重损失函数的AR-Net-WL网络相较使用AR-Net网络在计算代价没有显著提高的前提下，计算精度（R2与RMSE）有所提升。具体地，AR-Net-WL 相较于AR-Net 网络，训练集合的RMSE值由0.038 8降至 0.033 3，降幅约 14.2%。

表3 训练样本3 000 时AR-Net 和AR-Net-WL 网络的R2与RMSE指标Tab.3 R2 and RMSE indicators of AR-Net and AR-Net-WL networks (training samples=3 000)

为了进一步说明权重损失函数的作用，分别统计AR-Net 和AR-Net-WL这2种替代模型的污染物浓度场预测误差绝对值的最大值。由图6 可知，AR-Net-WL 网络的emax值相较AR-Net 网络更小，再次验证了AR-Net-WL 网络中添加的权重损失函数对提高污染源附近区域的预测精度的有效性，从而提高替代模型整体的预测精度。

图6 AR-Net和AR-Net-WL的emax频率Fig.6 emax frequency diagram of AR-Net and AR-Net-WL

3.3 正则项系数ωd的影响

构建替代模型时，应该从训练样本中尽可能学出适合所有潜在样本的“普遍规律”［25］，但是如前所述在训练样本不是很充足的情况下，很容易出现过拟合现象。针对过拟合现象，如果没有条件增加训练样本，可以考虑采用正则化方法（并不能完全解决）。下面讨论在样本数量较少的情形下，通过优化正则项系数提高替代模型的精度。为了找到最优正则化系数，算例中考虑5 个数量级范围内的30 个正则项系数值进行计算（训练样本为500）。具体地，设置ωd在2～ 7与10−7～ 10−3数量级组合，进行30次模型计算。

图7 为30 个ωd对应替代模型的测试样本集合RMSE值，其中A代表ωd的整数部分，B代表ωd的指数部分。在同一数量级下，随着ωd值的变化，RMSE值的变化规律不太明显；在10−7至10−5的数量级下RMSE值总体更小，对应替代模型精度更高；最小RMSE为0.063，明显优于未进行正则项系数优化的替代模型（训练样本为1 000对应的RMSE=0.068）。

图7 不同ωd对应替代模型的测试集合RMSE值（训练样本500）Fig.7 RMSE value for test set of surrogate model corresponding to different ωd values (training sample=500)

图8为训练样本数量为500得到的AR-Net-WL替代模型（选用最佳正则项系数ωd=3×10-7）对于某一随机选取的测试样本的预测结果。由图可知，替代模型的水头场和浓度场的预测结果与真实模型非常接近，这表明即使在训练样本较少的情形下（500 个训练样本）选用较好的正则项系数得到的AR-Net-WL替代模型同样具有良好的性能，可以有效地预测水头场和不同时刻污染物浓度场。