大型地下管网预测性运维多源监测数据融合决策方法
2023-03-10李明昊刘绪都
李明昊,冯 新,刘绪都,韩 阳
(大连理工大学 建设工程学部,辽宁 大连 116024)
为了适应经济、社会高速发展对能源的迫切需求,我国大力发展油气管道输送技术,2019年已经建成油气管道干线13.9×104km,预计至2030 年油气管道总里程将达到25×104~30×104km。在高速发展的同时可以预见,将有越来越多的管道进入服役的中后期,不同程度地面临老化失效的风险。管道一旦发生事故,不但会中断城市服务和工业生产,造成严重经济损失,并且通常导致人员伤亡和环境破坏,严重危害公共安全,社会负面效应难以挽回[1]。因此,为地下管道建立服役寿命预测模型以用于实施预测性的维护计划,已经成为国内外研究的关键问题之一。
从20世纪80年代开始,学者们对地下管道的失效机理和服役寿命预测进行了广泛研究,积累了重要的研究成果。Ahammed和Melchers[2]考虑了复杂应力和腐蚀的作用,基于应力分析模型和可靠度分析理论建立了地下管道失效概率分析模型,探索了地下管道的服役寿命预测方法。诸多学者在此基础上将预测模型进一步发展,Sadiq 等[3]针对铸铁管道提出了考虑内压、温度、覆土、交通、冻融荷载和腐蚀作用下的可靠度模型,该研究采用Monte Carlo(MC)模拟和敏感性分析得到了管道服役周期内各变量对失效概率的贡献情况。Amirat 等[4]又继续考虑了金属管道在焊接过程中产生的残余应力作用,提出了残余应力模型并使用可靠度软件PHIMECA计算分析了金属管道的可靠度。Mahmoodian 和Li[5]则研究了铸铁管在多种失效模式(均匀腐蚀导致的应力失效和局部腐蚀导致的断裂失效)的共同作用下管道的失效概率,对各变量进行了敏感性分析,并建立了运维策略。然而,目前地下管道领域的服役寿命预测模型均是建立在设计值或假设值上的,尤其是没有包括由地基沉降、土壤侵蚀、第三方扰动等引起的纵向弯曲响应。随着结构健康监测技术的发展,分布式光纤监测技术被广泛研究并被用于测量管道的纵向弯曲应力[6]。但是,现有的监测方法只考虑了单一目标,如应变或温度,没有进行充分融合。在实际工程中,被监测的纵向应变可能包含纵向弯曲应变和轴向热伸缩应变两部分,轴向热变形也可能由于不完全约束而没有完全转化为温度应力。因此,既不能直接由监测的纵向应变确定纵向弯曲应力,也无法仅使用单一的温度监测数据确定轴向热应力,需要将多源监测数据进行融合。在多源监测数据融合的基础上建立地下管道的服役寿命预测模型,可以使服役寿命的预测结果更准确地反映真实结构状态,因此在管道可靠性评价和制定运维策略方面具有重要意义。
本文以连续式地下金属管道为研究对象,根据其失效机理和基于贝叶斯公式的数据融合建立应力分析模型。考虑均匀腐蚀对结构的恶化作用,将服役寿命预测模型进一步扩展,融合可以反映真实结构状态的实时监测数据,为地下管道的首次运维检测计划提供更准确的决策依据。实例验证所提方法的有效性并为本研究的重要性提供案例证明。
1 方法建立
地下管网在长期服役过程中受到复杂的组合荷载的作用和结构承载力退化的影响。为了保证地下管道全生命周期内的正常服役,提出基于多源监测数据融合的预测性运维决策方法。如图1 所示,该方法包括基于多源监测数据融合的应力分析模型、考虑均匀腐蚀的结构退化模型和基于时变可靠度的运维决策模型等。
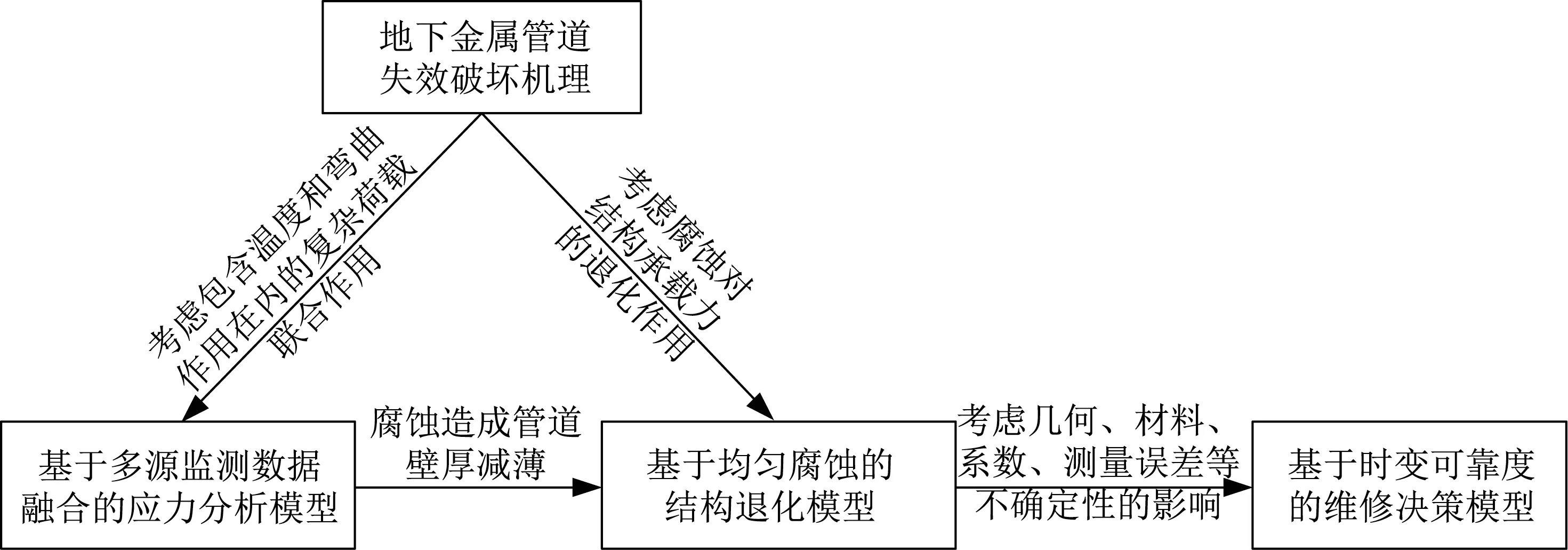
图1 基于多源监测数据融合的预测性运维决策方法技术路线Fig.1 Predictive maintenance decision-making method based on fusion of multi-source monitoring data
1.1 基于多源监测数据融合的应力分析模型
连续式地下薄壁金属管道的破坏形式可以分为2 种类型[7]:一类是由内压、覆土荷载和交通荷载导致的环向应力破坏;另一类是由热伸缩荷载、地基沉降和土壤侵蚀造成的纵向应力破坏。对于环向应力σh(x),已有大量研究讨论并构建了较为成熟的理论模型[8],如式(1)所示。其中内压P是最主要的失效因素,因此采用数字压力变送器进行实时测量,由内压产生的环向应力σh,P(x)根据式(2)确定;覆土荷载作为恒载可以按实际施工情况计算,由垂直土压力产生的环向应力σh,S(x)根据Spangler 等[9]提出的柔性管的应力计算式(式(3))确定;根据现有研究的参数敏感性分析结果[5],交通荷载对失效概率的贡献通常较小,因此建议采用定期巡检的方式对轮压值F进行统计估计,由交通荷载产生的环向应力σh,V(x)可根据式(4)确定。
式中:P为内压监测数据;D和δ分别为管道的内径和壁厚;km和kd分别为弯曲系数和变形系数,与基床有关;r为管道的内半径;E为管道弹性模量;表示垂直土荷载项,其中Cd为土压力系数,Bd和γ分别为管沟宽度和回填土容重;IcCtF/Le表示地面交通荷载项,其中Ic为动载系数,Ct为路面荷载作用系数,F为轮压荷载,Le为管道有效影响长度。
对于纵向应力,施工时的不均匀垫层、覆土回填时的地基沉降以及地质灾害等会不可避免地导致管道出现纵向的弯曲响应。然而弯曲变形发生的位置和幅值大小是高度随机的,无法提前预测[6],因此已有模型中并未充分考虑这一项。另一方面,地下金属管道被广泛应用于长输油气管道和市政供热管道。这些应用场景中往往会伴随着较大的温度荷载,故此类管道的规范也分别在应力分析中对温度荷载作了明确要求[10-12]。根据上述的地下金属管道失效机理分析,纵向应力σl(x)可总结为式(5)。其中内压的泊松效应引起的纵向应力σl,P(x)根据式(6)确定。
式中:σl,B(x)、σl,T(x)分别为纵向弯曲应力和轴向热应力;v为泊松比。
如上所述,荷载的不确定性导致了无法预测真实的结构弯曲变形,因此较为科学的方法是布设传感器对纵向弯曲应变进行实时监测。考虑到离散的点式监测技术不能满足管道这类长距离、大范围基础设施的测量要求,采用具有良好发展潜力的Brillouin 光纤应变传感器(Brillouin fiber optic strain sensor,BFOS),将分布式光纤应变和温度传感器均沿管道纵向布置在管道顶部以测量纵向应变,其中分布式光纤温度传感器为应变测量提供了温度补偿以及进行泄漏监测。对于轴向热应力,其产生的本质是周围土体的锚固作用限制了轴向热膨胀变形,因此温度差是最主要的影响变量,应采用数字温度传感器进行实时测量。
在实际工程中,为了防止轴向热应力过大而造成管道失效破坏,经常会在管道上安装波纹管等补偿器。以左端为固定支座、右端为波纹管的地下金属管道为例(图2),当管道出现温度差时,靠近补偿器的部分会发生一定程度的轴向伸缩来释放一部分热应力,形成过渡段。由于管-土的相互作用,管道的轴向伸缩将在锚固点处xg被完全约束,锚固点到固定端的部分形成了锚固段。因此,纵向应变测量结果包含了弯曲应变和热应变,不能直接获得纵向弯曲应力。同时,仅使用温度差数据也无法计算过渡段的轴向热应力,而仅依赖分布式应变数据又无法估计锚固段的热应力。综上,需要建立一种融合多源监测信息的方法以识别和估计纵向弯曲应力和轴向热应力。分布式光纤应变传感器和数字温度传感器分别独立获取了2类信息源{S1,S2}:S1和S2分别代表纵向应变数据∆εl(x)和温度差数据∆T(x)。观测空间包括4 类互不相容的假设{A1,A2,A3,A4}:分别表示沿管道的某一位置x受到的作用事件为无作用、弯曲作用、锚固段热作用、过渡段热作用。管道的温升变化通常仅持续数小时,外部荷载和管沟条件在这个过程中通常不会发生显著变化,因此互不相容假设是成立的。根据贝叶斯公式有

图2 安装补偿器的地下金属管道在温度荷载作用下的热变形示意Fig.2 Thermal deformation of an underground me⁃tallic pipe installed with a compensator un⁃der temperature loads
式中:P(Ai|S1,S2)为在2 个信息源{∆εl,∆T}下事件Ai为真的后验概率;P(S1|Ai)为在事件Ai的作用下信息源S1的条件概率;P(Ai)为事件Ai的先验概率,满足,在缺乏信息的情况下可认为各事件的先验概率相同[13]。
纵向弯曲应力σl,B(x)和轴向热应力σl,T(x)可以采用贝叶斯融合和数据融合的方法获得,具体算法如下:
(1)假设沿管道布设的分布式光纤传感器共测量得到N个应变测量点,定义第k个测量点的各事件后验概率为Pk(Ai|S1,S2),k=1,2,…,N,按式(7)计算所有测量点的各事件后验概率。
(2)在某一监测周期内,整个管道发生无作用或弯曲作用事件的概率按式(8)计算:
(3)在某一监测周期内,整个管道发生轴向热作用的概率及锚固点xg的位置按式(9)确定:
(4)使用最大后验概率(maximum a posteriori,MAP)和阈值的方式确定管道在某一周期内发生的荷载作用事件,如式(10):
式中:α为管道材料的线弹性系数;xg和Lg分别为地下管道在温度荷载作用下的锚固点位置和锚固段长度。
(7)若(Ai|S1,S2) 综上,本文在已有模型的基础上引入了实时监测的数据,并通过贝叶斯公式和数据融合获得了无法提前预测的纵向弯曲应力和轴向热应力,为更准确地预测管道服役寿命提供了应力分析的理论支撑。 美国管道和危险材料安全管理局(Pipeline and Hazardous Materials Safety Administration,PHMSA)2021年的报告显示,腐蚀是造成管道结构退化失效的最主要因素,占全部管道事故的23.3%[15]。腐蚀可分为均匀腐蚀和局部腐蚀。然而局部腐蚀在管道上发生的位置是随机的,无法提前预测,因此在实际工程中通常使用在线的无损检测手段确定腐蚀坑的位置和发展情况。本文旨在为新建管道提供首次检测运维计划的决策依据,只考虑均匀腐蚀的作用。当首次检测完成后,仍可在本文提供的框架下根据实测数据(位置、深度)继续引入局部腐蚀扩展模型和应力集中模型。采用广泛应用的幂函数模型描述均匀腐蚀的过程,如式(12): 式中:δc为均匀腐蚀的深度;k和n分别为腐蚀增长的系数和指数;t为管道已服役的时长。 腐蚀引起的管道结构退化过程可以认为是对管道壁厚的减薄过程,因此将式(12)的均匀腐蚀模型作为管道壁厚的被减项代入式(2)、(3)、(4)、(6)中便可以得到管道的结构退化模型。 所提出的应力分析模型和结构退化模型中的诸多几何、材料参数是设计值而并非实测值,与土、腐蚀相关的系数也往往具有很大的不确定性,传感器测量的数据也不可避免地存在着测量误差。因此,为了有效地考虑这些不确定性,提出了一种基于时变可靠度的运维策略模型。对于塑性的金属管道,Von Mises和Tresca失效准则被广泛使用,而断裂理论一般应用于局部缺陷(如腐蚀坑)情况下出现应力集中导致的结构失效。考虑到金属管道的应用场景有较高的安全要求,采用更为保守的Tresca 失效准则建立极限状态方程,如式(13): 式中:σeq(x,t)为管道服役至t年的当量应力;[σ]为管道材料的容许应力,或容许应力变化范围(适用于循环热荷载的安定性分析[16])。 由于方程(13)是高度非线性的,常用的方法是采用Monte Carlo 方法进行建模。将管道从安装运行到首次发生结构失效的时间定义为Tf,它可以视为一个随机变量。通过对式(13)给出的极限状态方程进行Monte Carlo模拟并对样本进行统计,便可以得到管道在任意位置x处失效时间Tf的概率密度函数f(x,Tf),因此,管道在任意位置x,服役了任意时长t,发生结构失效的累积失效概率可以按式(14)计算: 综上,本文在应力分析模型、结构退化模型和时变可靠度分析的基础上建立了随时间变化的结构失效概率模型。同时,该模型与现有的管道可靠性分析模型不同,它融合了反映真实结构状态的实时监测数据和传感器测量误差信息,因此使预测结果更逼近真实情况,为检测决策提供理论依据。根据累积失效概率,可以定义决策函数 式中:Tinsp为首次检测的时间;Tj为运行时间,年;Fthres为首次检测的寿命可靠性阈值,可由管道的目标可靠性指标确定;Nd为设计使用寿命。根据式(15),当新建管道的寿命可靠性指标达到规定阈值时,应采取检测和维护措施。在首次检测后,对腐蚀发展情况有了新的实测信息,可以对腐蚀扩展模型的参数使用贝叶斯方法进行更新,同时可以在本文的框架基础上继续引入局部腐蚀模型等。 结合实际工程案例来说明所提出方法的有效性和重要性。某新建市政供热管道,工作管采用Q235B钢,其一端连接固定支座,另一端连接波纹管补偿器。从固定支座后13.5 m开始布设监测光纤,测试长度为57.7 m。在管壁上安装DS18B20 数字温度传感器,SITRANS P DS III数字压力变送器布置在热力站的供水管和回水管上。根据1.1 节知,各事件的先验概率为:P(A1)=P(A2)=P(A3)=P(A4)=0.25。对应变和温度监测数据进行统计分析,在外部荷载干扰较小的情况下,概率分布结果如图3所示。采用实测数据的95%置信区间来确定各事件在不同信号源下的条件概率,结果见表1。将应力识别的判定阈值设定为0.7。此外,与管道材料、几何相关的变量服从的分布由实际施工确定,与传感器监测相关的变量服从的分布由标定的误差确定,与腐蚀、土等有关的系数服从的分布参考文献[2-3,5],所有随机变量和系数均服从正态分布且具体参数见表2。首次检测和运维的阈值设定为10−2。 表1 事件Ai的条件概率Tab.1 Conditional probability of Event Ai 表2 随机变量和系数的分布情况Tab.2 Distribution of random variables and coeffi⁃cients 在回填施工前,对市政供热管道进行了分布式光纤测量,其测量值作为施工阶段应变监测的基准值来观测纵向应变的变化。由DS18B20 测量的管道温度为22℃。在经过了管沟回填、路面压实等施工后,管温测量值为24℃,则温差变化为2℃。经过温度补偿后,纵向应变的测量结果如图4a所示,其每个事件在管道任意位置的后验概率结果如图4b、4c、4d、4e所示。在本次施工阶段的监测周期内,整个管道发生各事件的概率计算为 :。因此施工阶段发生的纵向应变被识别为纵向弯曲应变。 图4 施工后纵向应变测量结果与识别计算过程Fig.4 Measurement and identification of longitudinal strain after construction 在加压和升温前,对市政供热管道进行分布式光纤测量,其测量值作为运行阶段应变监测的基准值来观测纵向应变的变化。由DS18B20 测量的管道温度为23℃。在经过了加压和升温后,管温测量值为57℃,则温差变化为34℃,由数字压力变送器测量的管道内压为1.0 MPa。经过温度补偿后,纵向应变的测量结果如图5a所示,其每个事件在管道任意位置的后验概率结果如图5b、5c、5d、5e 所示。图5f绘制了整个管道的轴向热作用的后验概率与锚固点位置相关的函数,可以由最大概率确定出锚固点的位置为38.141 m 处。在本次运行阶段的监测周期内,整个管道发生各事件的概率计算为:。因此运行阶段发生的纵向应变被识别为轴向热应变。 图5 升温后纵向应变测量结果与识别计算过程Fig.5 Measurement and identification of longitudinal strain during operation 综上,施工阶段产生的纵向弯曲应力和运行阶段产生的轴向热应力的计算结果如图6所示。工程案例表明,在施工阶段由于覆土荷载、垫层不平整以及不均匀沉降等因素,导致了显著的纵向弯曲应力。此外,在运行阶段由于管-土复杂的相互作用、土壤摩擦不均匀等,导致了过渡段的轴向热应力波动较大。根据实测数据,可以确定锚固段和过渡段的最危险位置分别为2.36 m和56.77 m。由于这些位置更容易发生损坏,因此选取这些最危险位置进行基于时变可靠度的失效分析。 图6 纵向弯曲应力与轴向热应力计算结果Fig.6 Calculation of longitudinal bending stress and axial thermal stress 根据供热管道的设计规范[12],容许应力变化范围应按照安定性分析理论选取 {2σy,σb}中(σy和σb分别为管材的屈服强度和抗拉强度)的较小值,即2σy。Monte Carlo 模拟的样本数为25 万个,统计得到了到达容许应力极限状态所需时间的概率密度函数,如图7a所示。无论是在锚固段还是过渡段,考虑了纵向弯曲应力的模型中在设计服役年限[0,50]内(区域1)的概率密度均高于不考虑弯曲应力的模型。通过对区域1 的概率密度函数进行积分,可获得设计服役年限期间的失效概率,如图7b所示。计算结果显示,在考虑纵向弯曲应力的模型中,位于过渡段的56.77 m 处首次检测对应的时间为服役后的第9年,这比不考虑纵向弯曲应力的现有模型计算的结果提前了8.2年,缩短至1/2。其次,在同一年份下,过渡段的失效概率比锚固段更高,这说明地下管道可能在过渡段率先发生失效破坏,其本质是由于过渡段发生了更大的纵向弯曲应力,这与规范和现有模型仅考虑锚固段的轴向热应力相违背。 图7 时变可靠度与运维决策计算过程Fig.7 Calculation of time-dependent reliability and maintenance decision 显然,本文所提出的模型在多源实测数据的支持下充分考虑了当前的真实结构状态,获得了比现有的管道可靠度模型更准确的预测结果。从所研究的实际工程可以发现,由施工阶段的各种不利因素导致的弯曲响应对失效概率的影响可能十分显著,这说明管道发生失效破坏的时间很可能比现有可靠度模型[2]预测的首次检测维护计划更早,无法实现预防性的维护作用。因此,本文提出的多源监测数据融合的运维决策模型对地下金属管道实现预测性维护和安全管理具有重要意义。 为了保证地下管道全生命周期内的正常服役,提出了基于多源监测数据融合的预测性运维决策方法。针对复杂荷载作用下连续式地下金属管道的失效破坏机理,提出了多源监测数据融合的应力分析模型,该模型解决了实际工程中单一监测目标无法估计纵向弯曲应力和轴向热应力的问题。在此基础上基于均匀腐蚀的结构退化模型和时变可靠度理论提出了预测性运维策略支持模型。该模型比目前广泛使用的地下管网应力评价模型增加了不可预测部分的实测信息,即纵向弯曲应力,因此能够更加准确地评价和预测地下管网服役安全。 某实际供热管道的研究结果表明,施工过程中由覆土荷载、垫层不平整以及不均匀沉降等因素导致的弯曲响应较大,对运维决策结果产生了明显影响,在地下管道的服役安全评价及性能预测中不应忽略。需要指出的是,本文只提供了基于均匀腐蚀的首次检测维护计划的决策依据,未来应在首次检测获得结构退化的实测信息后进一步考虑局部腐蚀作用,利用新的实测信息对失效概率进行更新,提供下一次检测维护的决策依据。对于非连续式地下管道(如承插式球墨铸铁管、混凝土管等)仍需针对其典型失效模式和监测与检测技术研究全生命周期预测性运维决策支持的理论和方法。 作者贡献声明: 李明昊:算法设计和编程、数据处理和分析、文稿撰写。 冯 新:论文选题、参与研究的构思和设计、对重要学术性内容做出关键性修订和定稿。 刘绪都:数据采集。 韩 阳:传感器布设。1.2 基于均匀腐蚀的结构退化模型
1.3 基于时变可靠度的运维决策模型
2 工程案例
2.1 概况


2.2 应力估计结果

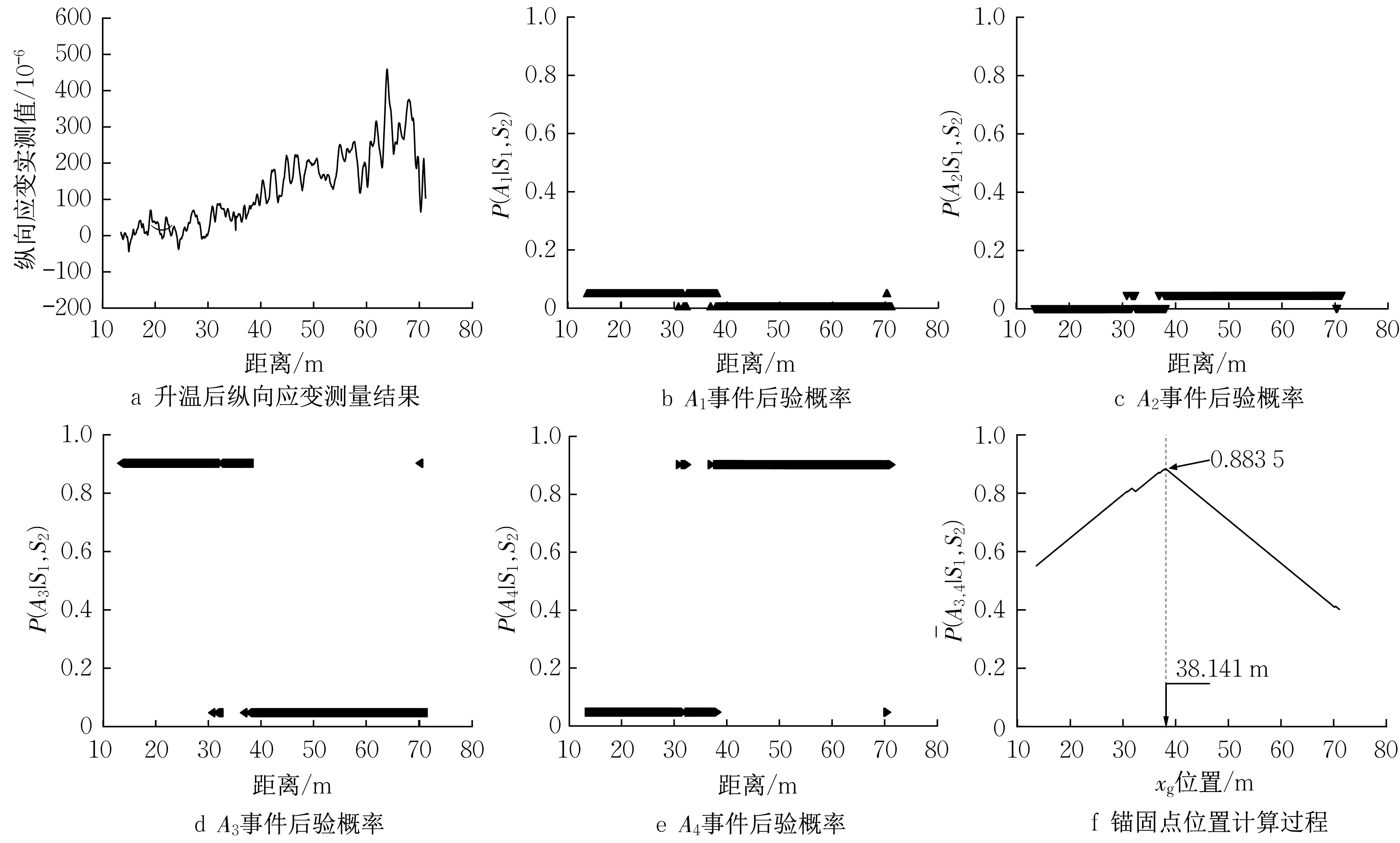
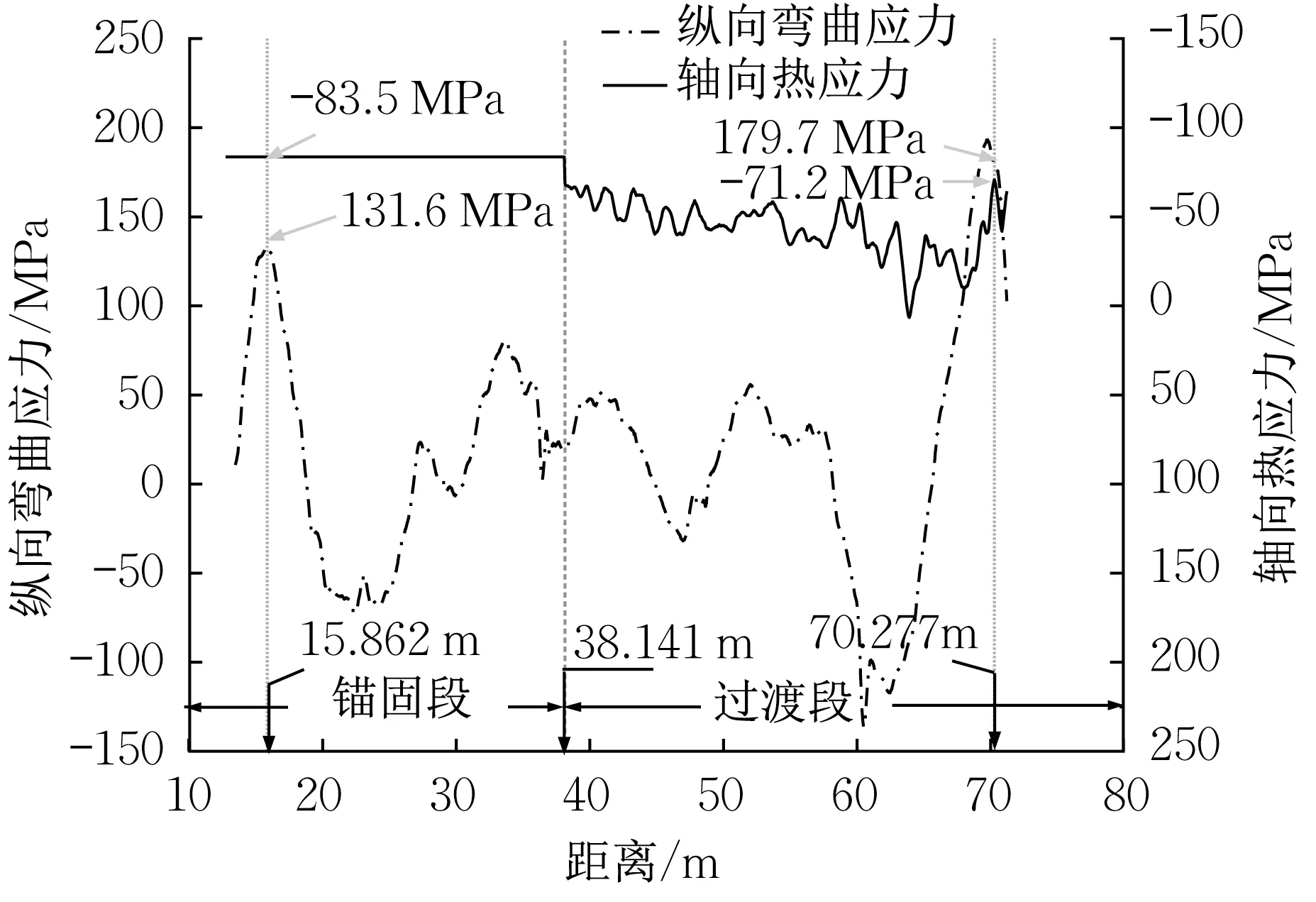
2.3 运维决策结果
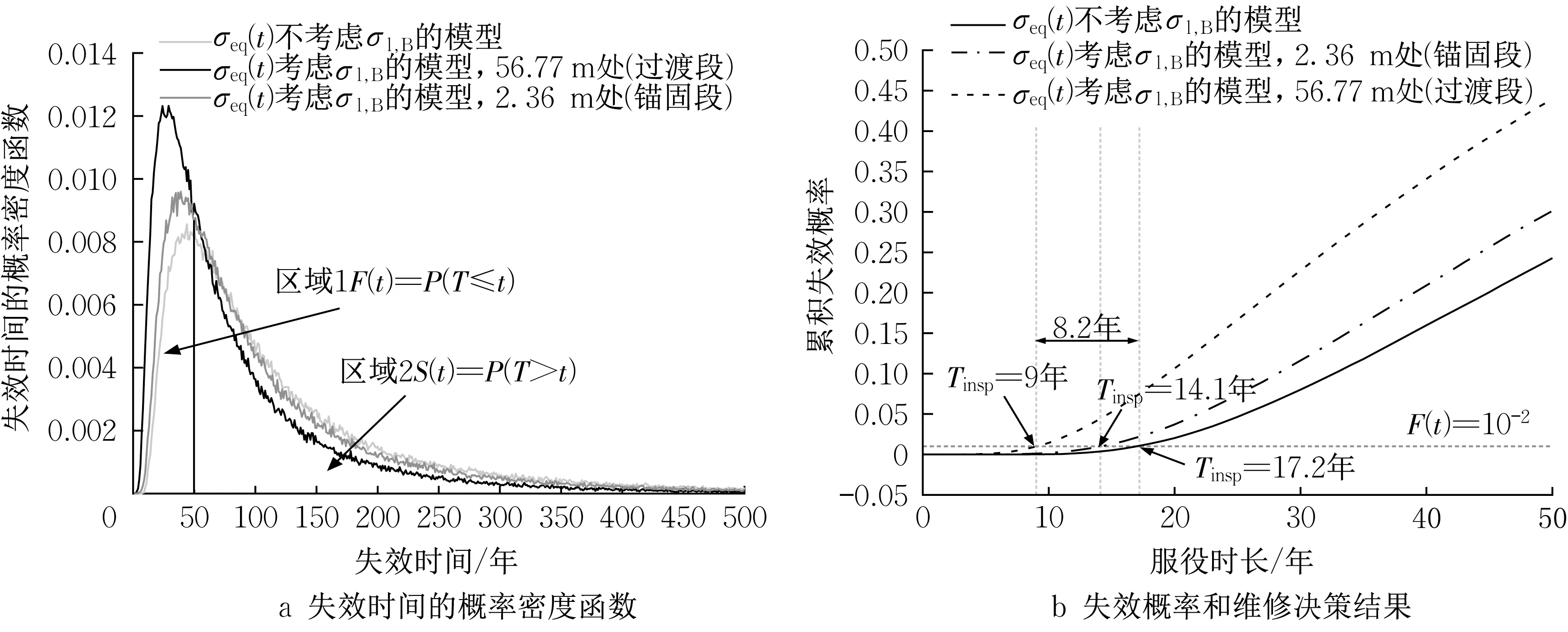
3 结论
