多约束多输入拦截器姿轨一体化复合控制
2023-03-09郭建国郭宗易王国庆
彭 谦, 郭建国,*, 郭宗易, 王国庆
(1. 西北工业大学航天学院精确制导与控制研究所, 陕西 西安 710072;2. 中国运载火箭技术研究院研发部, 北京 100076)
0 引 言
临近空间动能拦截器是一种采用姿轨复合控制,依靠全捷联红外被动式导引头实现自主寻的,最终通过碰撞毁伤临近空间高超声速目标的高速度、高精度拦截器[1-3]。全捷联红外导引头与拦截器固联,测量值为体视线角,这导致导引头视场约束与拦截器姿态耦合[4-6];姿轨复合控制系统由安装在不同位置的侧喷发动机组成,根据侧向直接力的作用位置不同,能够同时产生力、力矩两种控制量[7-8]。上述视场约束和执行机构特性均会导致严重的姿态与轨道控制耦合。姿态与轨道的耦合使得制导控制系统呈现高维、强耦合和强非线性特点,给控制器设计带来极大挑战[9]。
在对控制精度要求高的场景中,应特别注意姿轨耦合问题[10-11]。然而,现有的关于姿轨控制动能拦截器的研究采用分而治之的策略分别设计制导律和控制律[8,12],忽略了姿态与轨道控制耦合,以牺牲控制精度为代价简化控制器设计。相比之下,制导控制一体化通过测量状态直接同步生成姿、轨发动机控制指令,不仅能够充分考虑姿轨耦合,还能够避免制导系统向控制系统传递制导信息的过程[13-15]。将姿控和轨控视为一个整体,采用一体化方法设计姿轨复合控制系统,能够充分发挥执行机构的性能,从本质上提高拦截器的机动能力和控制精度,避免能量的浪费或内耗。特别地,对于燃料有限的姿、轨控发动机,姿轨一体化复合控制有极大的研究价值。
复合控制的本质是多输入控制系统,文献[16]将多输入转换为单输入处理,且转换要求系统参数非时变。文献[17-18]将子系统间的耦合视为不确定项,在控制律设计中忽略了耦合的影响。上述研究没有重视多输入系统中的耦合问题,无法被应用于姿轨一体化复合控制。
除此之外,临近空间动能拦截器还面临着状态约束问题[19-21]。障碍Lyapunov函数被广泛用于约束系统状态,然而基于现有研究,障碍Lyapunov函数需要借助反步法才能扩展至高阶系统,同时可引入低通滤波器避免反步法的“指数爆炸”[4,22-24]。然而,低通滤波器不可避免地会引入滤波误差,降低控制器的控制精度。现有研究缺乏对真正意义上的、不采用反步法的高阶系统状态约束的研究。
针对临近空间动能拦截器,本文提出了姿轨一体化复合控制律,主要贡献如下:
(1) 考虑姿轨耦合并引入体视线角和交会角约束,建立了基于姿轨复合控制的临近空间动能拦截器制导控制一体化模型;
(2) 基于反正切函数设计了包含状态约束信息的映射函数,提出了一种简便、适用性广的状态约束方法,在不改变控制器结构的前提下,实现了高阶多输入耦合系统的状态约束;
(3) 针对多输入多输出的临近空间动能拦截器制导控制系统,充分考虑姿轨耦合,不使用反步法,提出了一种高精度、低能耗的姿轨一体化复合控制律,在满足其体视线角约束和交会角约束的同时,实现了多个控制任务。
1 临近空间动能拦截器制导控制系统建模
1.1 全捷联姿轨复合控制拦截器建模
临近空间动能拦截器采用姿、轨控发动机作为控制输入,姿、轨控发动机均垂直于弹体纵轴安装。轨控发动机安装在拦截器质心,提供力控制量,通过改变加速度调整其飞行弹道;姿控发动机安装在拦截器尾部,同时提供力、力矩控制量,以提供力矩控制量为主,用于修正姿态。
以纵向平面为例,拦截器与目标的相对运动如图1所示。
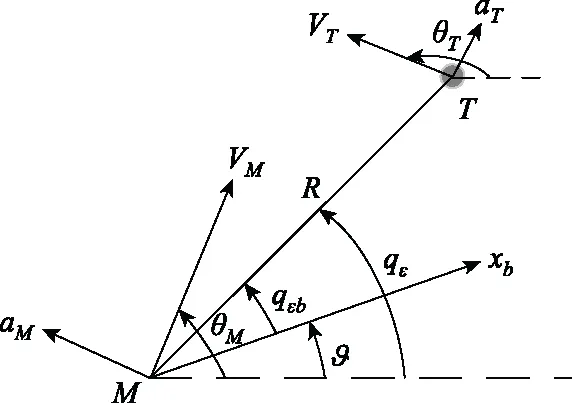
图1 拦截器-目标相对运动示意图Fig.1 Schematic diagram of interceptor-target relative motion
图1中,M代表拦截器;T代表拦截目标;R代表弹目相对距离,qε代表目标线方位角,VM、VT分别代表拦截器和目标的速度,aM、aT分别代表拦截器和目标的加速度,θM、θT分别代表拦截器和目标的弹道倾角;Mxb与拦截器纵轴重合,指向拦截器头部;ϑ代表拦截器俯仰角,qε b代表拦截器体视线角。
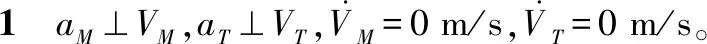
考虑临近空间的气动力作用,根据图1中的拦截器-目标相对几何关系,可建立临近空间动能拦截器运动学模型如下[25]:
(1)
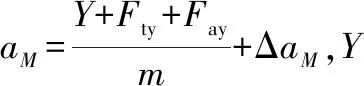
临近空间动能拦截器的动力学模型可建立如下[26]:
(2)
(3)
其中,
MFay=-Fay(xp-xg)
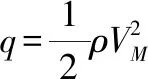
姿、轨控发动机不能调整推力大小,只能调整脉冲宽度。参考文献[27],假设发动机一旦开启,推力大小恒定不变,建立姿、轨控发动机控制输入归一化模型如下:
(4)
式中:Tt、Ta分别代表轨控、姿控发动机控制周期;Fte、Fae分别代表轨控、姿控发动机的固定推力;It=FteTt、Ia=FaeTa分别代表一个控制周期内轨控、姿控发动机能提供的最大冲量;τt、τa分别代表轨控、姿控发动机的开启时间占空比;τt、τa若为负,则代表反向发动机提供推力。
由于动能拦截器采用全捷联导引头,参考图1,动能拦截器的体视线角与目标线方位角、拦截器俯仰角之间有如下的几何关系:
qε b=qε-ϑ
(5)
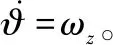
考虑到全捷联导引头视场范围限制,qε b需满足以下约束:
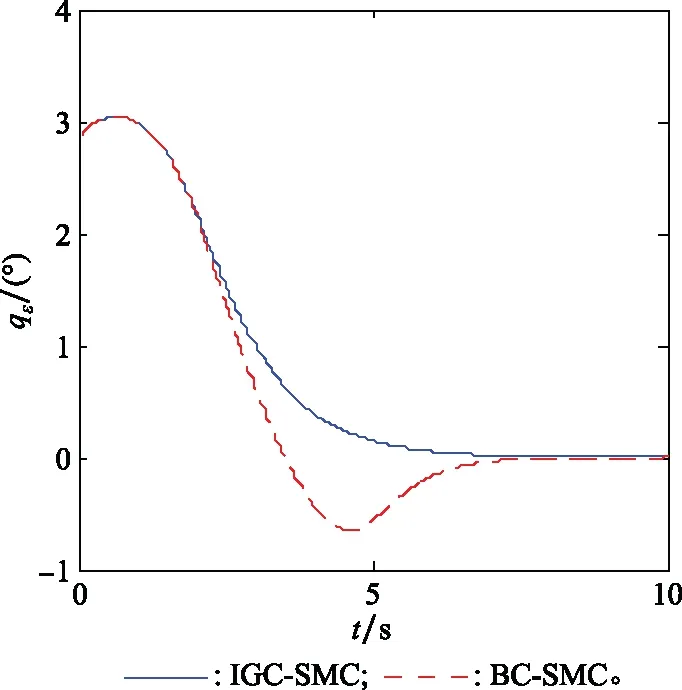
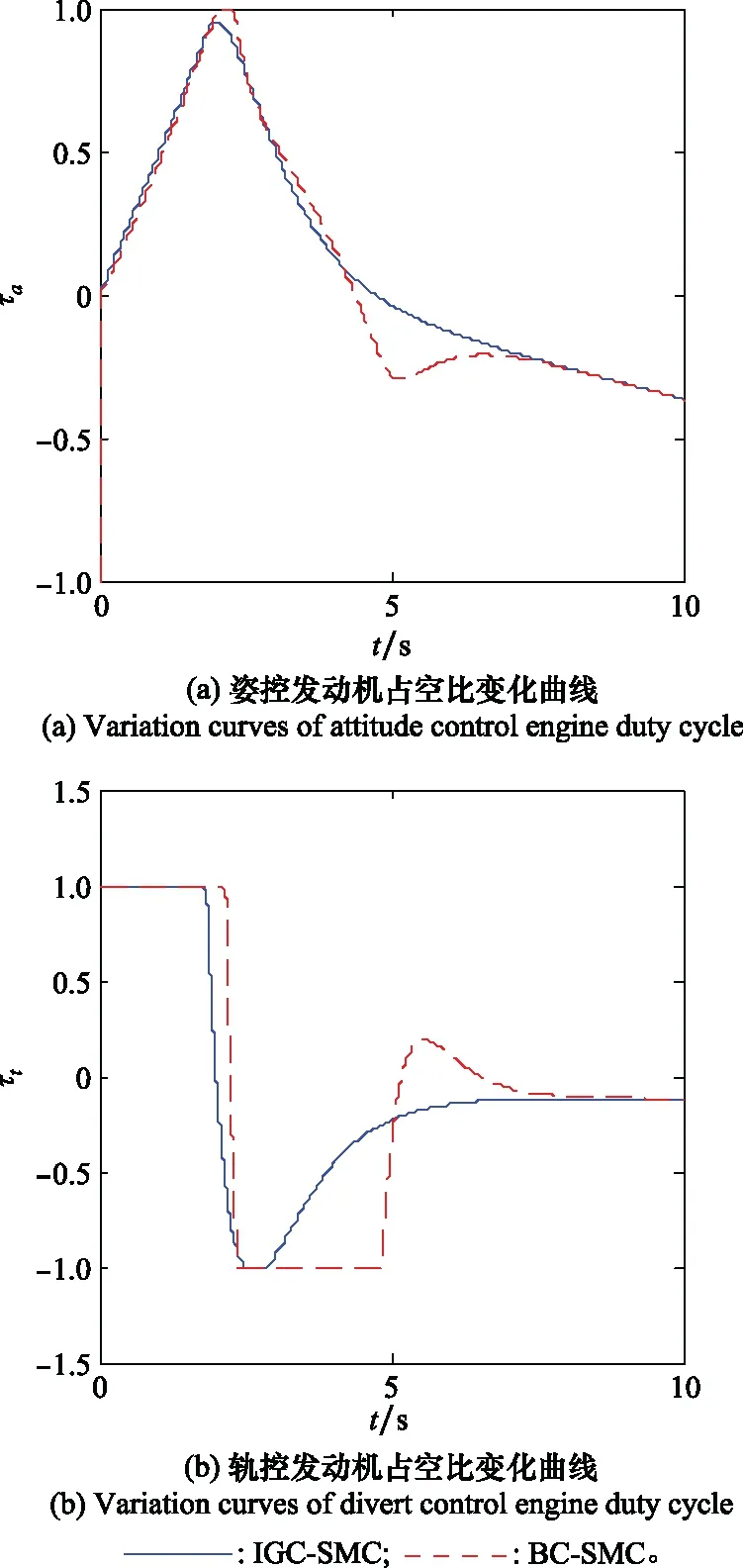
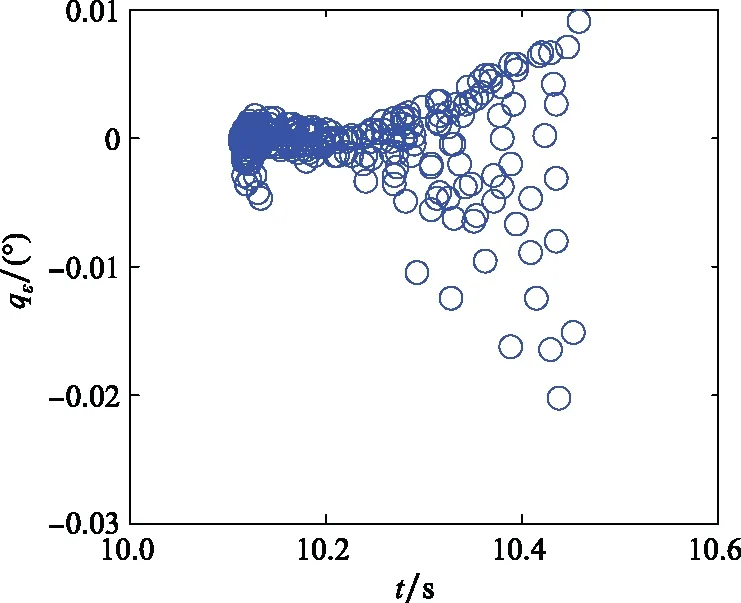
εmin (6) 式中:εmax、εmin分别代表导引头最大、最小视场角,均为常数。 (7) 假设2在临近空间动能拦截器制导控制一体化系统(7)中,非匹配不确定干扰di(i=3,4)是有界的,即|di|≤σi,σi为已知正数[28-29]。 针对动能拦截器制导控制系统中存在的非匹配不确定干扰,引入了文献[29]的扩张干扰观测器(extended disturbance observer, EDO)如下: (8) 引理1通过选择合适的参数λi1、λi2,EDO估计误差的范围[29]满足: (9) 全捷联导引头导致拦截器姿态与弹道耦合。根据拦截器的材质、飞行速度等,拦截器会采用将全捷联导引头安装在弹体侧面的方式,以避开弹头的热流密集区[30-31]。因此,为使得拦截器体视线角满足约束(6),设计可包含任意体视线角约束的映射函数如下: -ε∞ (10) 式中:ε∞=εmax-ε0=-εmin+ε0。 基于式(7)和式(10),定义函数如下: x1=ν(z1)ε∞+ε0 (11) 定义映射函数ν(z1)如下: (12) 结合式(11)和式(12),可得 (13) 有 (14) 当z1→∞时,x1→εmax;当z1→-∞,x1→εmin。因此,z1可作为被约束状态x1的映射函数,在后续的控制器设计中,用z1取代x1,即可确保x1始终满足约束式(6)。 假设3x1的初值x1(0)满足εmin 包含体视线角约束的映射函数式(13)可适用于对称和非对称导引头视场,即无论全捷联导引头是安装在弹头或弹体侧面,均可通过在控制器中引入式(13)以实现视场约束。 动能拦截器需要在精准命中目标的前提下满足交会角约束和体视线角约束。由式(7)可知,姿轨复合控制属于异类多输入耦合控制系统,轨控发动机只能提供调整弹道的力控制量,无法主动调控拦截器姿态;姿控发动机可同时提供力和力矩两种控制量(其中以力矩控制作用为主)调整拦截器姿态。考虑姿轨耦合,基于干扰观测器、包含体视线角约束的映射函数和高阶滑模控制,针对临近空间动能拦截器设计姿轨一体化复合控制律。 基于制导控制一体化模型(7),将映射函数z1与滑模变结构控制结合,设计滑模面如下: (15) 考虑到干扰观测器的观测误差,结合式(7),定义滑模面趋近律如下: (16) 式中:φ11、φ12为正常数。为抑制抖振,用饱和函数sat(s1)代替符号函数sign(s1)[32], 交会角约束属于终端约束,通过对qε的控制实现。因此,基于制导控制一体化模型式(7)设计滑模面如下: (17) 式中:x2c代表x2的期望值;c2为正常数。 考虑到干扰观测器的观测误差,结合式(7),定义滑模面趋近律如下: (18) 式中:φ21、φ22为正常数;sat(s2)与sat(s1)相同。 U=-B-1[Φ1S+Φ2sat(S)+G] (19) 定理1临近空间动能拦截器的姿轨一体化复合控制律式(19)控制下的系统在存在体视线角约束和交会角约束时是有界稳定的,其控制输出x1和x2的收敛范围分别为 (20) (21) 证明 -|s1|(φ11|s1|+φ12|sat(s1)|-|a11|D3- |a12|D4)-|s2|(φ21|s2|+φ22|sat(s2)|-|a21|D3) (22) (23) (24) 将式(24)代入式(15),有 (25) |x2|(c2|x2|-γ2-c2|x2c|) (26) (27) 说明一体化复合控制律控制下的系统是有界稳定的。 证毕 本文仿真均在拦截器拦截末段的纵向平面下完成。临近空间动能拦截器的飞行速度为VM=1 500 m/s,初始位置为xm=0 m,ym=20 000 m,其他状态量初值为α=0°,ϑ=0°,θM=0°,ωz=0°/s;目标飞行速度为VT=1 500 m/s,加速度为aT=40 m/s2,初始位置为xt=30 000 m,yt=21 500 m;初始弹道倾角为θT=175°。全捷联导引头的视场范围约束为εmax=15°、εmin=-15°,姿、轨控发动机可提供的直接力分别为|Fay|≤3 000 N、|Fty|≤20 000 N。 控制期望为x1c=0°,x2c=0°;控制器参数为φ11=1,φ12=1,φ21=1,φ22=1,c1=3,c2=1,λi1=10,λi2=10。 仿真步长为1 ms。考虑到弹目相对运动速度很快,为尽可能消除仿真步长给脱靶量计算造成的偏差,利用线性插值估算脱靶量。定义整个仿真过程中共有n个采样点,取j=1,2,3,…,1 001,kj=0.001(j-1),则第n-1至第n个采样点间的第j个线性插值点可描述为 (28) 式中:xm(n-1)、ym(n-1)和xt(n-1)、yt(n-1)分别代表第n-1采样点拦截器和目标的位置;xm(n)、ym(n)和xt(n)、yt(n)分别代表第n个采样点拦截器和目标的位置。 可得各插值点对应的弹目相对距离R(j)为 (29) min[R(j)]即为脱靶量,与min[R(j)]对应的目标线方位角qε即为交会角。 下面将从一体化设计、映射函数约束、蒙特卡罗打靶三方面验证本文提出的姿轨一体化复合控制律的性能。 姿轨一体化复合控制律将姿控与轨控系统视为一个整体,即制导控制一体化。在不考虑约束的情况下,对比基于制导控制一体化的滑模控制律(integrated guidance and control-based sliding mode control, IGC-SMC)与基于反步法的滑模控制律[13](backstepping control-based sliding mode control, BC-SMC)的控制性能差异,仿真结果如表1所示。 表1 拦截器碰撞状态 由表1中的拦截器碰撞状态可以看出,IGC-SMC和BC-SMC均可顺利命中目标,IGC-SMC所用拦截时间略短;考虑到姿轨控复合控制本身具有响应速度快的特性,一体化设计可以略微提升系统的响应速度,但效果不明显。 图2和图3所示分别为IGC-SMC和BC-SMC控制下的拦截器飞行弹道和目标线方位角变化曲线。结合图4控制输入曲线,经分析可知,相较于IGC-SMC,BC-SMC控制指令起伏更大,更易使得执行机构输入饱和,致使拦截攻击目标和目标线方位角跟踪过程控制效果较差。同时,由图4控制输入曲线和表2发动机所需冲量经分析可知,IGC-SMC发动机需用冲量显著小于BC-SMC,尤其是轨控发动机需用冲量。这说明一体化设计相较于反步法设计具有更高的控制效率,能够有效减少能量的消耗,对于提升燃料有限的姿/轨控拦截器性能有很大帮助。 图2 IGC-SMC和BC-SMC控制下的拦截器飞行弹道Fig.2 Interceptor’s trajectory under the control of IGC-SMC and BC-SMC 图3 IGC-SMC和BC-SMC控制下的目标线方位角Fig.3 Curves of line-of-sight orientation angle under the control of IGC-SMC and BC-SMC 图4 IGC-SMC和BC-SMC控制输入曲线Fig.4 IGC-SMC and BC-SMC control input curves 表2 姿/轨控发动机所需冲量 姿轨一体化复合控制律(19)本质是基于EDO的被约束滑模控制器(EDO based constrained sliding mode controller, EDO-CSMC)。通过对比EDO-CSMC、被约束滑模控制器(constrained sliding mode controller, CSMC)、基于EDO的滑模控制器(EDO based sliding mode controller, EDO-SMC)以及滑模控制器(sliding mode controller, SMC)这4种控制器的仿真结果,验证映射函数约束和干扰观测器的有效性。 为提高仿真结果对比的可靠性,CSMC、EDO-SMC及SMC中的参数与EDO-CSMC相同。在飞行5 s后,引入干扰d4=25cos(0.5πt)。通过对比拦截器的碰撞状态、控制输入等评估4种控制器的性能,假设体视线角超出视场范围,不丢失目标,有仿真结果如表3所示。 表3 拦截器碰撞状态 由表3拦截器碰撞状态可知,拦截器在EDO-CSMC、CSMC、EDO-SMC及SMC的控制下,脱靶量满足命中需求,基本满足交会角约束qε=0°。以上结果证明,若目标始终在导引头视场范围内,以上4种控制器均可实现拦截。 图5展示了在4种控制器的控制下,体视线角变化曲线与视场约束的关系。结合图5可以看出,SMC对干扰的抑制能力最差,并且无法满足视场约束;EDO-SMC由于引入了EDO,对干扰有一定的抑制作用,但仍无法保障视场约束;实际上,体视线角超出视场约束范围,代表着拦截器导引头丢失目标,EDO-SMC和SMC控制下的拦截器不能成功拦截目标。CSMC相较于SMC和EDO-SMC,具有更强的鲁棒性,能够确保视场约束得到满足;EDO-CSMC在CSMC的基础上引入EDO,在保证视场约束的条件下进一步抑制了干扰,控制效果最好。同时,在5 s前,4种控制器作用下的体视线角变化曲线几乎重合,说明EDO、映射函数约束的引入不影响控制器的基本性能。 图5 体视线角变化曲线Fig.5 Variation curves of body line-of-sight angle 在300次蒙特卡罗仿真中,体视线角均在视场约束范围内。同时,结合图6所示的体视线角跟踪误差平均值和方差、图7所示的脱靶量蒙特卡罗打靶结果和图8所示的交会角蒙特卡罗打靶结果可以看出,在随机气动参数摄动和目标机动下,拦截器可以顺利命中目标,并且满足体视线角约束和交会角约束,这表明本文设计的姿轨一体化复合控制律具有较强的鲁棒性。 图6 体视线角蒙特卡罗打靶结果Fig.6 Monte Carlo test result of body line-of-sight angle 图7 脱靶量蒙特卡罗打靶结果Fig.7 Monte Carlo test result of miss distance 图8 交会角蒙特卡罗打靶结果Fig.8 Monte Carlo test result of impact angle 基于反正切函数设计了包含状态约束信息的映射函数,能够在不影响滑模控制器基本框架的前提下实现高阶多输入耦合系统中的状态约束。 针对临近空间动能拦截器制导控制系统,充分考虑姿轨耦合,基于滑模控制和视场约束的映射函数提出了姿轨一体化复合控制律,在不采用反步法的前提下实现了高阶系统控制,避免了滤波误差,提升了控制精度。 姿轨一体化复合控制律能够在满足体视线角约束和交会角约束的同时实现对目标线方位角和体视线角的跟踪控制,避免了制导指令向控制系统传递的过程,提高了控制效率,减少了姿、轨控发动机的燃料消耗。1.2 制导控制一体化模型
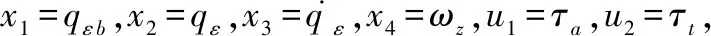
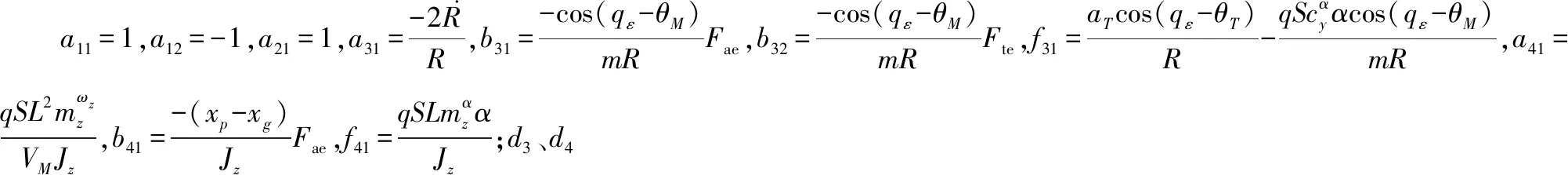
2 姿轨一体化复合控制系统
2.1 干扰观测器
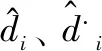
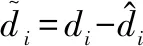
2.2 基于体视线角约束的映射函数
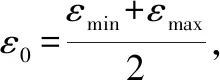
2.3 状态约束下的姿轨一体化滑模控制律
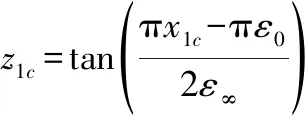
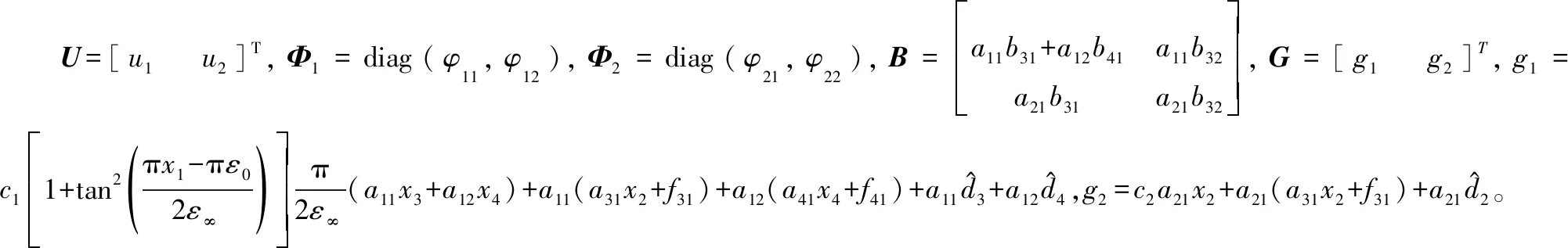
2.4 稳定性证明
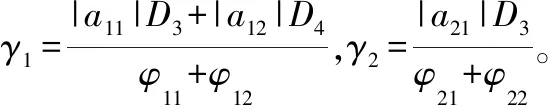
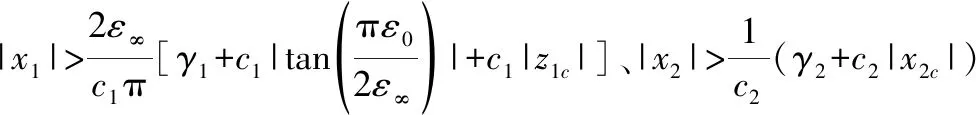
3 仿真分析
3.1 一体化设计有效性验证



3.2 映射函数约束性能验证
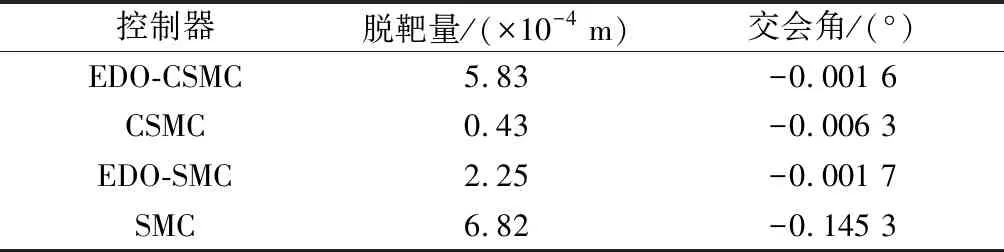
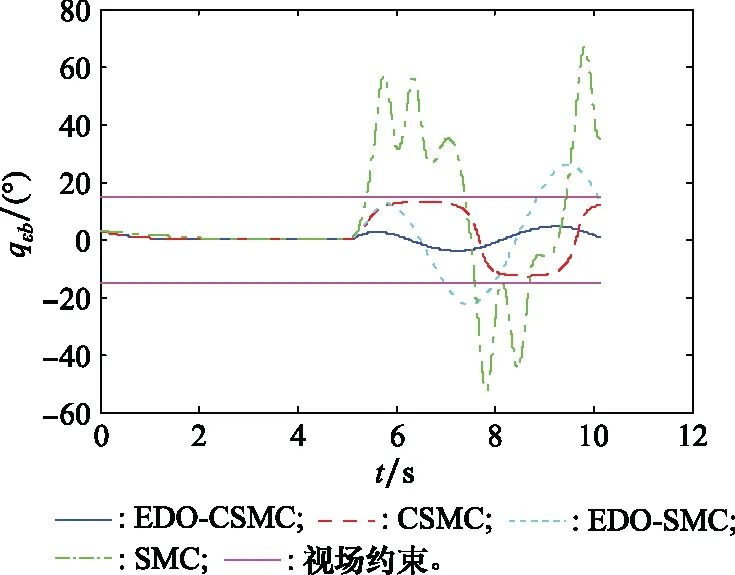
3.3 蒙特卡罗打靶仿真
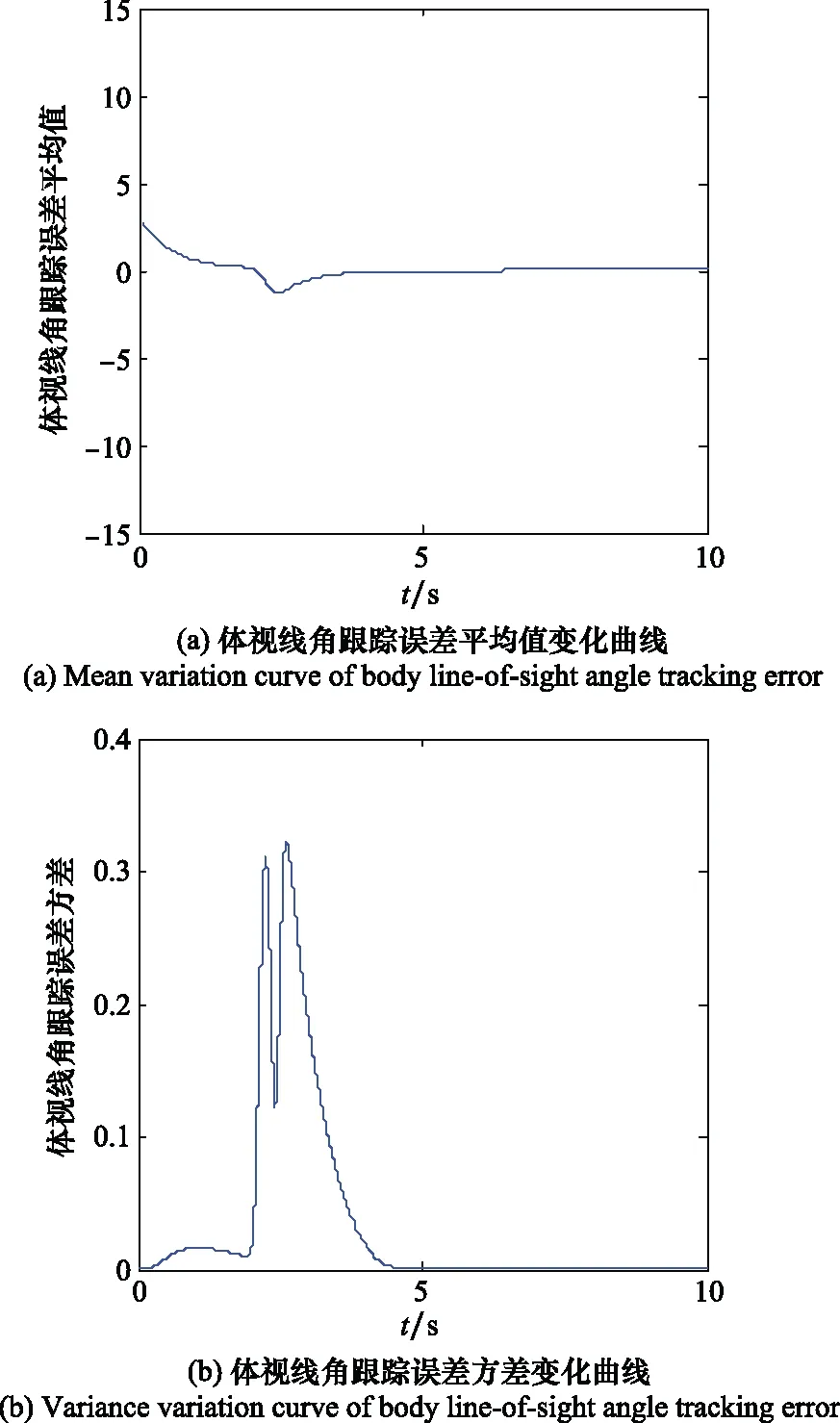
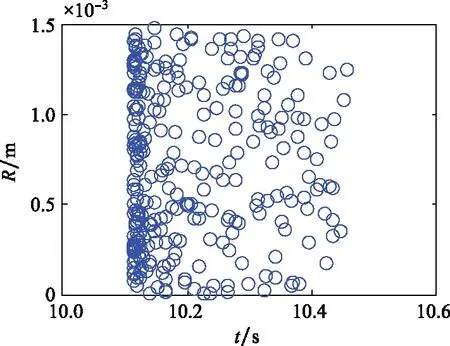
4 结 论
