长三角城市群最优人口规模及其空间格局优化

童玉芬 韩佳宾

(首都经济贸易大学劳动经济学院，北京 100070)

引 言

城市群是我国推进新型城镇化的主体形态，高质量发展的城市群可以优化区域发展格局，带动整个经济高质量发展。以城市群为单位的区域发展规划已上升为国家战略，《国家新型城镇化规划(2014—2020年)》明确提出要以城市群为主体形态，科学规划建设城市群，推动大、中、小城市和小城镇协调发展。长江三角洲城市群(以下简称为长三角城市群)作为中国经济发展最活跃、开放程度最高、创新能力最强的城市群之一，是我国经济发展的一个重要增长极。近年来，国家不断加大对长三角城市群的重视。2016年6月《长江三角洲城市群发展规划》提出，要将长三角城市群建设为面向全球、辐射亚太、引领全国的世界级城市群。优化长三角城市群的人口空间格局，促进大、中、小城市和小城镇协调发展，提升城市品质和居民生活质量，可以为我国新型城镇化提供探索经验。

根据《长江三角洲城市群发展规划》，长三角城市群包括上海市、江苏省、浙江省、安徽省的64个城市，其中1个直辖市、25个地级市和38个县级市(见表1)，面积为21.17万平方千米。长三角城市群是中国经济发展水平最高的区域，2020年长三角城市群GDP达到21.2万亿元，占全国GDP总量的20.9%，远高于我国其他城市群的经济水平。根据第七次全国人口普查数据，2020年长三角城市群范围内常住人口为1.65亿人，占全国城市群常住人口的14.36%，人口密度达到771.5人/平方千米。其中城区常住人口为8875.87万人，(1)城区常住人口数据来源于2020年《中国城市建设统计年鉴》。占整个长三角城市群常住人口的53.77%。从内部空间结构看，人口主要集中在上海、杭州、宁波、合肥、南京等超大、特大城市中，常住人口占比接近40%，内部人口空间分布表现为向首位和核心城市集聚的典型特征，其中首位度2城市指数、4城市指数和11城市指数分别为2.99、1.23、1.26。但是相比于标准的城市群位序—规模规律，以及城市群内部的最大经济产出效率而言，当前长三角城市群的人口空间分布是否合理，以及城市人口规模是否符合各自的产出最优目标，在学术界还没有专门的研究。分析了解城市群的人口发展及空间格局，测算长三角城市群内部的最优人口规模，优化城市群人口空间格局，可以引导人口合理流动，进一步释放城市化的巨大潜力，培育经济增长的新动能，这直接关系到长三角区域一体化和城市群的高质量发展，关系到国家整体城市群发展战略的实现，有助于为不同城市发展与人口调控找到适合的路径，为政策制定提供参考。

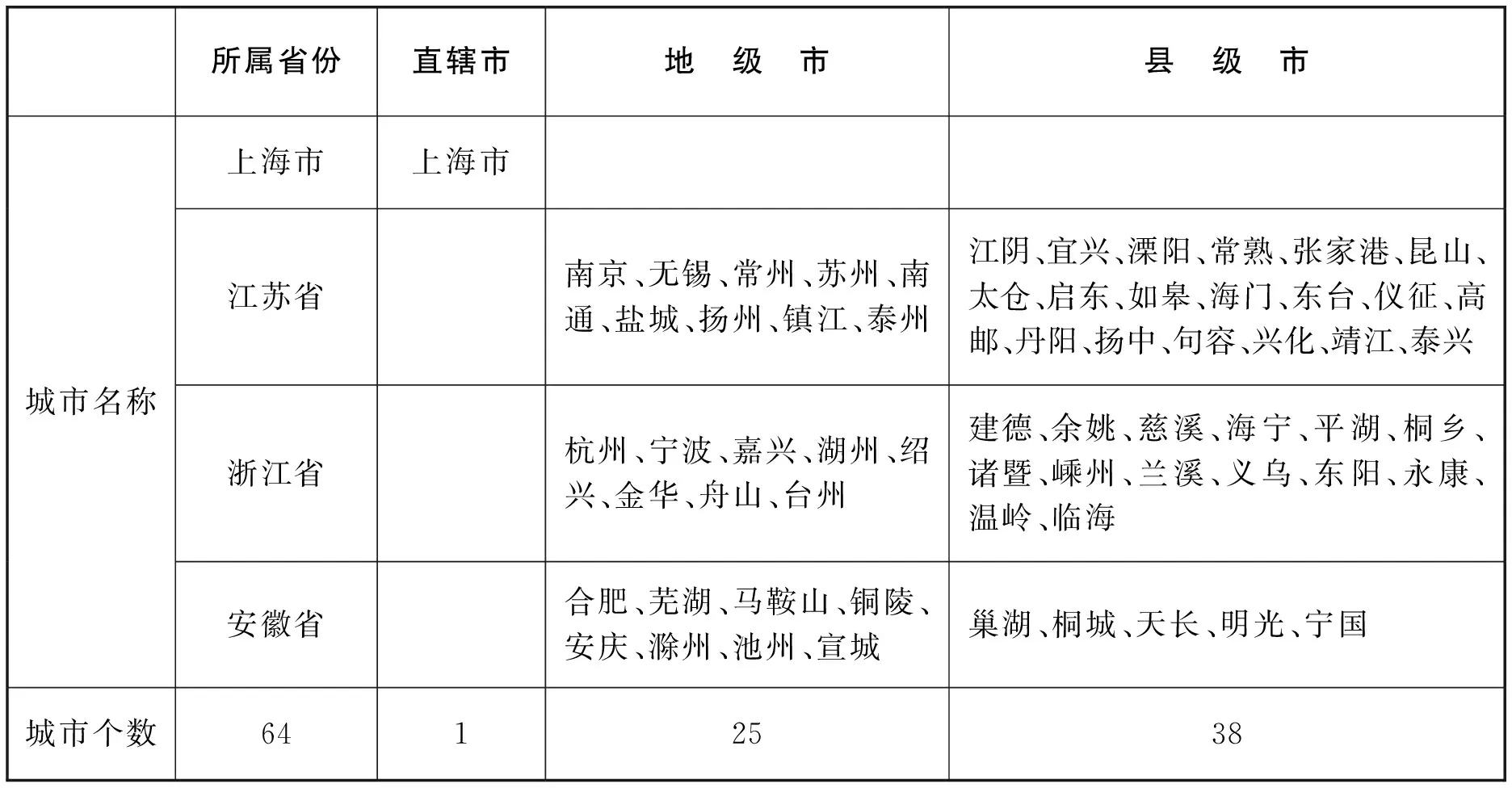
表1 长三角城市群范围及所属城市

一、文 献 综 述

国内外学者对于城市最优人口规模已有多年研究。最优人口规模与适度人口、人口承载力等概念相近也经常被混用。一些学者基于城市资源环境测算人口的承载力，(2)Kyushik Oh, Yeunwoo Jeong, Dongkun Lee, eds.,“Determining Development Density Using the Urban Carrying Capacity Assessment System,” Landscape and Urban Planning, vol.73, no.1 (2005), pp.1-15.(3)参见李振福：《城市交通系统的人口承载力研究》，《北京交通大学学报》(社会科学版)2004年第4期，第76— 80页。(4)参见郭志伟：《北京市土地资源承载力综合评价研究》，《城市发展研究》2008年第5期，第24—30页。(5)参见童玉芬：《北京市水资源人口承载力的动态模拟与分析》，《中国人口·资源与环境》2010年第9期，第42— 47页。或者基于资源、生态、经济等因素研究城市适度人口，(6)David Pimentel, Rebecca Harman, Matthew Pacenza, eds.，“Natural Resources and an Optimum Human Population,” Population & Environment, vol.15, no.5 (1994), pp.347-369.测度方法有模糊综合评判(7)参见林晓娟、房世峰、杜加强：《基于综合承载力的北京市适度人口研究》，《地球信息科学学报》2017年第11期，第1495—1503页。、可能-满意度模型(8)参见童玉芬、王静文、梁钊：《资源环境约束下的中国适度人口研究》，《人口研究》2016年第2期，第3—11页。、双向寻优(9)参见徐琳瑜、杨志峰、毛显强：《城市适度人口分析方法及其应用》，《环境科学学报》2003年第3期，第355— 359页。等方法。还有学者通过城市产出最大化计算城市最优人口规模，王小鲁和夏小林对城市规模收益和外部成本进行分析，计算了我国城市的合理人口规模区间。(10)参见王小鲁、夏小林：《优化城市规模 推动经济增长》，《经济研究》1999年第9期，第22—29页。也有学者以新经济地理学为理论基础，建立了城市人口规模与城市产出的关系，并计算城市最优人口规模，(11)Chun-Chung Au, J. Vernon Henderson，“Are Chinese Cities Too Small?” The Review of Economic Studies, vol.73, no.3 (2006), pp.549-576.(12)参见梁婧、张庆华、龚六堂：《城市规模与劳动生产率：中国城市规模是否过小?——基于中国城市数据的研究》，《经济学(季刊)》2015年第3期，第1053—1072页。这类方法从城市中消费者的效用函数和生产者的生产函数出发，以经济产出或劳动生产率最大化为优化目标，测度满足城市经济效率最高的人口规模。

人口空间格局优化的研究与最优人口规模研究既有联系又有区别。但一般来说，区域内单个城市人口规模最优并不意味着区域内城市之间人口空间结构最优，因此人口空间结构优化研究自成体系。这方面的研究目前主要包括3类：(1) 基于人口空间分布特征的分析与判断，提出人口分布优化意见。人口空间分布特征采用的方法有：人口集中指数(13)参见廖传清、郑林：《长江中游城市群人口分布与城镇化格局及其演化特征》，《长江流域资源与环境》2017年第7期，第963—972页。(14)参见闫东升、孙伟、王玥等：《长江三角洲人口分布演变、偏移增长及影响因素》，《地理科学进展》2020年第12期，第2068—2082页。、基尼系数(15)参见邓丽君、张平宇、李平：《中国十大城市群人口与经济发展平衡性分析》，《中国科学院研究生院学报》2010年第2期，第154—162页。(16)参见苏飞、张平宇：《辽中南城市群人口分布的时空演变特征》，《地理科学进展》2010年第1期，第96—102页。、莫兰指数(17)Yu-Hsin Tsai，“Quantifying Urban Form：Compactness versus ‘Sprawl’,” Urban Studies, vol.42, no.1 (2005), pp.141-161.(18)参见董青、刘海珍、刘加珍等：《基于空间相互作用的中国城市群体系空间结构研究》，《经济地理》2010年第6期,第926—932页。；(2) 使用能够反映城市群内部城市规模等级结构的指标对人口空间分布结构进行判断，如齐普夫指数(19)Gilles Duranton, “Delineating Metropolitan Areas：Measuring Spatial Labour Market Networks through Commuting Patterns，”The Economics of Interfirm Networks, vol.4 (2015), pp.107-133.(20)参见王振波、方创琳、胡瑞山：《中国城市规模体系及其空间格局Zipf-PLE模型的评价》，《地球信息科学学报》2015年第6期，第682—688页。、分形维数(21)Charles Dietzel, Hakan Oguz, Jeffery J. Hemphill, eds., “Diffusion and Coalescence of the Houston Metropolitan Area：Evidence Supporting a New Urban Theory,” Environment and Planning B：Planning and Design, vol.32, no.2 (2016), pp.231-246.(22)参见曾鹏、黄图毅、阙菲菲：《中国十大城市群空间结构特征比较研究》，《经济地理》2011年第4期，第603— 608页。、MONO指数(23)参见黄妍妮、高波、魏守华：《中国城市群空间结构分布与演变特征》，《经济学家》2016年第9期，第50—58页。；(3) 通过对城市人口与资源环境、经济社会协调合理性评价，提出人口分布优化意见，主要使用耦合协调性模型、不一致指数(24)参见钟业喜、陆玉麒：《鄱阳湖生态经济区人口与经济空间耦合研究》，《经济地理》2011年第2期，第195— 200页。(25)参见贺三维、邵玺：《京津冀地区人口—土地—经济城镇化空间集聚及耦合协调发展研究》，《经济地理》2018年第1期，第95—102页。。

以城市群为分析单元研究其最优人口规模和人口空间格局优化，相对以城市为分析单元来说是一个比较新的话题，因为它不仅涉及区域，还涉及城市群内规模不等的城市之间的关系。一些学者将城市群看作一个区域整体，或是将内部城市看作若干个区域进行研究，采用上述资源环境承载力、适度人口规模、城市产出最大化等方法，得到城市群总体或内部单个城市的最优人口规模，(26)参见彭文英、刘念北：《首都圈人口空间分布优化策略——基于土地资源承载力估测》，《地理科学》2015年第5期，第558—564页。(27)参见熊鹰、姜妮、李静芝等：《基于水资源承载的长株潭城市群适度规模研究》，《经济地理》2016年第1期，第75— 81页。(28)参见杨子江、张剑锋、冯长春：《中原城市群集聚效应与最优规模演进研究》，《地域研究与开发》2015年第3期，第61—66页。或者对城市群人口空间分布特征进行分析，提出城市群人口优化意见。(29)参见杜忠潮、黄波、陈佳丽：《关中—天水经济区城市群人口经济与资源环境发展耦合协调性分析》，《干旱区地理》2015年第1期，第135—147页。(30)参见陈刚、刘景林、尹涛：《城市群产业、人口、空间耦合协调发展研究——以珠三角城市群为例》，《西北人口》2020年第2期，第114—126页。但也有学者将城市群看作由规模不一的城市组成的综合体系，研究城市群内部的最优人口空间结构。目前学界针对城市群人口空间结构的合理性评价研究集中于位序—规模法则，众多研究认为，可以通过研究城市规模分布的变化与齐普夫定律的关系来判断城市群人口空间分布的合理性。(31)参见范晓莉、黄凌翔：《京津冀城市群城市规模分布特征》，《干旱区资源与环境》2015年第9期，第13—20页。(32)Gilles Duranton, “Delineating Metropolitan Areas：Measuring Spatial Labour Market Networks through Commuting Patterns，” The Economics of Interfirm Networks, vol.4 (2015), pp.107-133.(33)参见王振波、方创琳、胡瑞山：《中国城市规模体系及其空间格局Zipf-PLE模型的评价》，《地球信息科学学报》2015年第6期，第682—688页。还有学者进行经济学内涵的改进，将城市收益、损耗的分形特征与人口规模的分形特征联系，建立城市群最优空间结构模型。(34)参见赵璟、党兴华：《基于分形理论的城市群最优空间结构模型与应用》，《西安理工大学学报》2012年第2期，第240—246页。

已有研究为本文提供了良好的基础，但总体来看，还存在以下几个进一步研究的空间：首先，现有城市群人口优化研究或针对最优人口规模，或针对城市群内部人口空间格局优化，很少能够同时考虑城市最优人口规模和城市群人口空间结构优化；其次，现有较多城市群人口空间研究缺乏城市体系空间视角，将城市群的内部城市看作不同区域的组合，未考虑城市之间的等级序列或辐射关系；第三，对长三角城市群内部各城市的最优人口规模及空间格局关系的直接测度几近空白。基于此，本文运用集聚经济理论，以城市产出最大化作为城市人口规模优化目标构建理论模型，并结合城市体系位序—规模法则中的齐普夫标准分布指数，测算基于城市群人口空间格局优化目标的各城市人口规模，以期为不同城市发展与人口调控找到适合的路径，为政策制定提供参考。

二、研究思路和理论模型推导

(一) 研究思路与步骤

本文以长三角城市群的人口空间结构优化为最终目标，同时结合单个城市的最优规模，得到在城市群人口空间结构优化下各城市的最优人口规模。具体思路和步骤如下：首先，确定城市群的最优人口空间体系结构标准。位序—规模法则是从城市位序与规模的关系来考察一个城市体系的人口分布。本文采用该法则中的齐普夫指数为1，作为长三角城市群人口空间格局优化的目标，具体原理和依据见后文。其次，计算城市群首位城市的最优人口规模。为了得到长三角城市群首位城市的最优人口规模，本文借鉴新经济地理学理论，推导出在城市最大产出时的人口规模。具体理论模型推导过程以及参数计算见后文。最后，确定长三角城市群内各城市在符合最优空间结构模式下的人口规模。将长三角城市群首位城市上海市的最优人口规模代入城市位序—规模法则中，在齐普夫指数为1的标准状态下，得到长三角城市群在最优空间格局下的其余城市人口规模。

(二) 人口空间格局优化指标的确定及依据

在城市群内部，层次不同、规模不一的城市, 通过质和量的组合, 形成了城市等级规模分布，该分布揭示了城市群内城市位序—规模的分布规律。1949年G.K.齐普夫(George K. Zipf )提出在经济发达国家中，一体化城市体系的城市规模可用简单公式表达为：Pr=P1/R，式中Pr是第R位城市的人口规模，P1是最大城市的人口规模，R是Pr城市的位序。后来，洛特卡(Lotka)将其发展为一种一般化模型：Pr=P1/Rq，对数变换为：lnPr=lnP1-qlnR，q是常数，即齐普夫指数。当q=1时，公式变为Pr=P1/R，即不同位序R的城市人口规模分别等于首位城市人口规模P1的1/R，城市群内各城市人口规模按照从大到小的等级序列按比例减小，呈现一种合理的城市等级序列分布状态。因此，学者们将q=1作为合理分布的标准，并将其称为齐普夫标准；当q>1时，表明城市群中城市人口主要集中在核心大城市，人口分布过度集中；当q<1时，表明城市群中人口较多地分布在中小城市中，人口分布过度分散。

根据本文计算和检验，长三角城市群内部的人口位序—规模分布呈现显著的分形特征，城市规模与位序高度相关，基本符合位序—规模分布规律。2020年长三角城市群的齐普夫指数为1.18，略高于齐普夫指数等于1的标准分布，说明长三角城市群从空间角度看人口相对过度集聚在首位城市中。

(三) 最优人口规模的理论模型推导

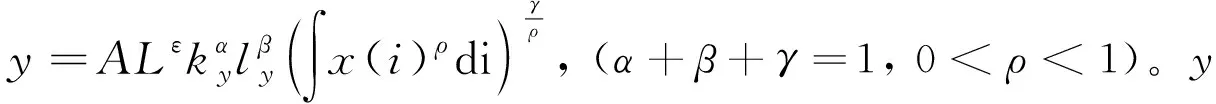
城市的总产值为：

(1)

总产值可以表示为最终产品价格P和产量y的乘积。

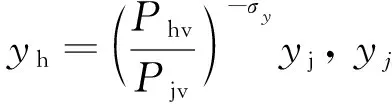
(2)

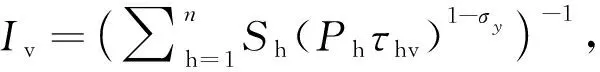
(3)

可得城市j生产的最终产品价格为：

(4)

(5)

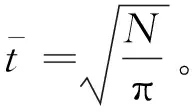
(6)

式(6)代入式(5)可将L替换为N，得到：

(7)

公式两边除以N，得到人均产出Y/N公式：

(8)

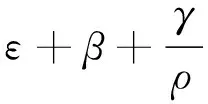
ln(Y/N)=lnA+1/σylnMP+αln(K/N)+

(9)

对式(9)进行二阶泰勒级数展开式，得到：

ln(Y/N)=lnA+1/σylnMP+αln(K/N)+

[a1N-a2N2-a3N×MS+a4MS+a5MS2]

(10)

其中，a1、a2、a3、a4和a5为参数，令K/N不变，在最大化产出条件下，解得最优规模极值点，即最优城市人口规模：

N*=(a1-a3MS)/2a2

(11)

三、长三角城市群首位城市最优人口规模计算

(一) 参数计算过程及结果

1. 计量模型构建

为了得到式(11)的参数，需要构建计量模型：

(12)

式(12)为基本回归模型，其中城市人口规模N是关键解释变量，用城市城区常住人口表示，(Y/N)it、(K/N)it、MPit、MSit分别表示i城市t期的人均产量、人均资本、市场潜力、产业结构，Xit表示i城市t期其余控制变量，μi表示与i城市相关的未观测因素，λt为时间效应，ηit为随机扰动项，α1、α2、α3为对应参数，Nit为i城市t期的人口规模。该计量模型存在不可观测因素带来的内生性问题，引入被解释变量的滞后项可一定程度解决解释变量与残差的相关性,于是构造动态面板模型(13)为：

ln(Y/N)it=α1ln(K/N)it+α2lnMPit+α3ln(Y/N)it-1+α4Xit+

(13)

(Y/N)it-1表示i城市t-1期的人均产出。动态面板模型的回归有差分GMM和系统GMM两种方法。差分GMM容易受弱工具变量的影响导致系数估计精度较差，系统GMM估计量结合了差分方程和水平方程，提高了估计效率。因此，本文对比报告固定效应模型、差分GMM、系统GMM的结果。

2. 变量选择及数据来源

本文还选择了其他几个控制变量，包括城市的人力资本、公共基础设施、政府公共支出、对外开放、科技创新、城市的土地面积。根据卢卡斯(Robert E. Lucas, Jr.)的人力资本模型，人力资本(Edu)是影响城市总产出的重要因素，较高的人力资本水平促进技术水平和经济集聚，对城市产出有正向影响，用人均教育经费支出表示。公共基础设施(Road)对城市有效运行产生影响，且作为公共品被生产者使用，选取与经济发展内生性较弱的人均城市道路面积表示。政府支出(Fin)可调节消费和投资，影响城市总产出，用人均地方政府公共支出表示。对外开放程度(Fdi)越高，会扩大本地市场规模, 这有助于厂商利用规模经济效应发展，城市利用外资越多，则表明该城市对外开放程度越高，用人均实际使用外资额衡量。科技创新(Tec)对城市产出有拉动作用，可持续促进经济增长的潜力释放，用人均专利授权量表示。同时，控制城市的土地面积，用建成区面积(Land)表示对土地的使用量，表2为变量解释。

由于县级市数据获取的局限，本文使用2009—2020年长三角城市群26个地级市的数据进行回归分析，所有数据均来源于《中国统计年鉴》《城市建设统计年鉴》《中国城市统计年鉴》以及各省市统计年鉴，表3是变量的描述性统计结果。

表3 描述性统计

3. 模型参数计算结果

表4报告了模型(13)得到的估计结果。因为固定效应结果不显著，差分GMM未通过Sargan检验，系统GMM通过Sargan检验，说明系统GMM工具变量的选取有效，回归结果更具可信性。因此选择系统GMM的回归结果得到式(11)的参数值a1=0.0009003，a2=0.00000015，a3=0.0006925。

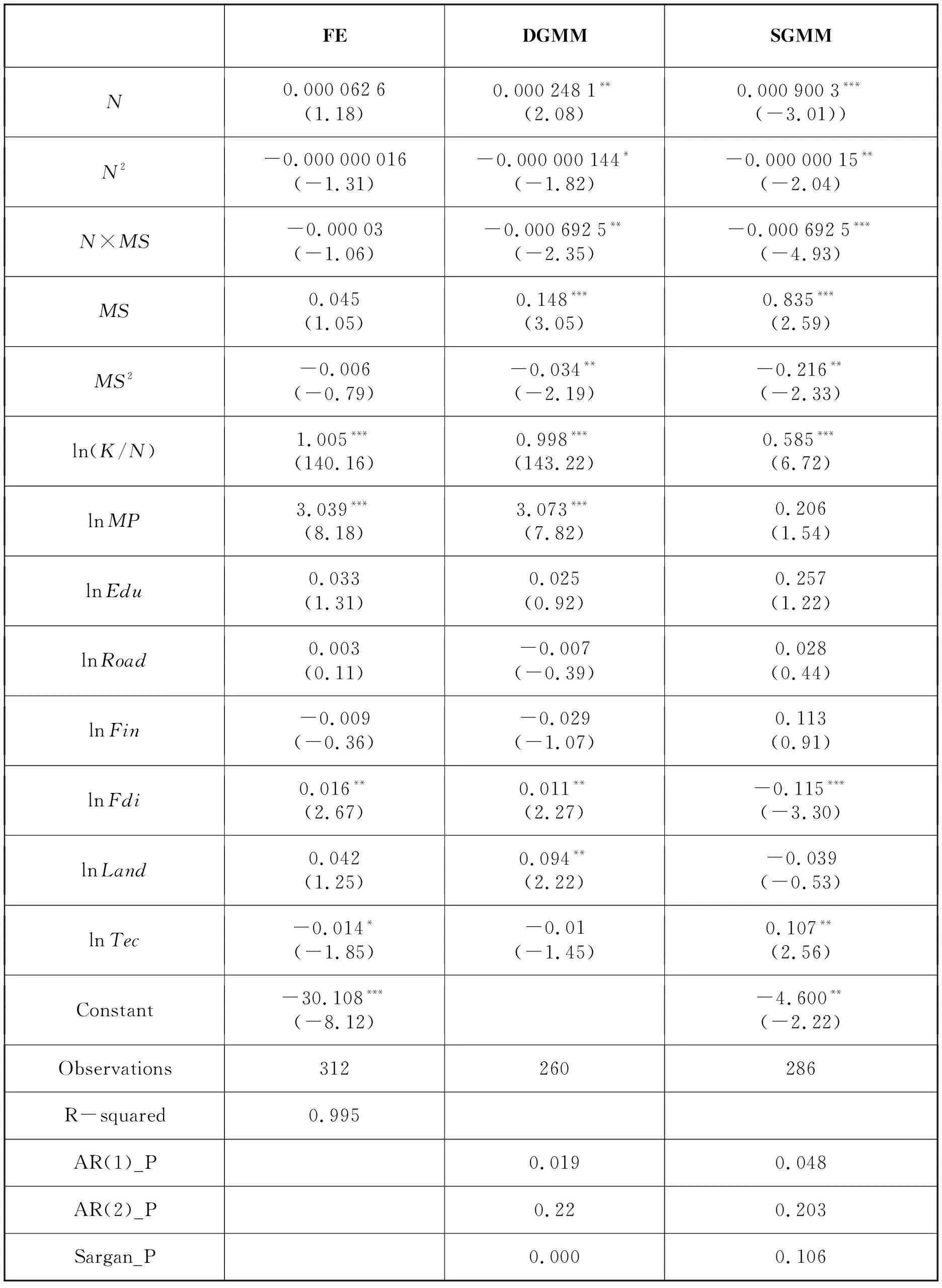
表4 回 归 结 果

(二) 长三角城市群首位城市上海市的最优人口规模计算结果

将上述参数值和上海市的二、三产业结构比值0.363代入式(11)得到长三角城市群首位城市上海市的最优人口规模为2161.95万人。

四、最优空间格局下的最终测算结果

将上海市最优人口规模代入位序—规模公式：Pr=P1/Rq，其中P1=2161.95，令q=1，求得城市群内其余城市的人口规模。计算结果见表5。

表5 长三角城市群满足最优规模下的各城市人口规模及实际人口

可以发现，长三角城市群在满足齐普夫最优人口规模的前提下，目前实际人口规模大于最优人口规模的城市有6个，包括上海、合肥、宁波、苏州、常州、无锡，说明这些城市目前人口规模较大，需要适当限制。而另外20个城市的实际人口规模小于最优人口规模，说明这些城市人口还未达到最优人口规模，需要继续集聚人口。尤其是身为长三角城市群次首位城市的南京和杭州，人口集聚不足，应该引起重视。此外，长三角城市群还表现为中小城市实际规模普遍小于最优规模，城市群中人口在中小城市集聚不足。

对比长三角城市群城市规模等级划分标准，可以得出目前长三角城市群超大城市人口规模过大、特大城市人口规模不足、大城市人口分布相对合理、中小城市人口规模过小的基本结论。

五、基本结论与政策启示

测算长三角城市群最优人口规模和人口空间格局优化，得到如下基本研究结论以及政策启示：

第一，通过计算，我们认为在城市群人口优化的研究中，可以同时考虑城市群人口空间格局优化与单个城市的最优人口规模，并实现二者的有效结合。因此，在城市群的规划建设中，既要考虑单个城市的最优规模，同时也要考虑城市之间的人口空间格局优化，只有将二者统一起来，才能实现人口在城市群内合理分布，推动长三角城市群区域一体化和高质量发展。城市群规划既要明确每个城市的发展定位及发展阶段，也要充分考虑城市群内各城市产业结构和人口规模的合理配置，调整产业布局，促进产业合理分工，避免产业恶性竞争。此外，增强各城市之间经济联系，综合考虑城市现有基础和发展条件，推进产业对接合作，构建优势互补、良性互动的产业发展体系，充分发挥城市群协同合作的优势。

第二，本研究计算结果表明，长三角城市群中的绝大多数城市都存在集聚不足的现象，尤其是除上海外的其他几个特大城市和众多中小城市，因此需要通过多种方式进一步集聚人口，增大这些城市的人口规模。尤其是南京市、杭州市人口集聚不足，吸纳人口潜力大，可作为吸引上海市人才回流的主要城市，加强与上海市的经济联系，完善长三角的交通基础设施网络，提高城市间交通便利，有利于完善城市融入地区的联系网络。城市群内中小城市普遍人口集聚不足，应继续加强城市公共基础设施建设、提供各项保障就业服务，吸引大城市人口回流，鼓励人口在城乡之间转移。这不仅有利于整个城市群人口的整体空间优化，而且有利于这些城市集聚效益的进一步发挥。

第三，从计算结果看，上海市的人口规模过大，处于过度集聚的状态。从城市规模经济来说，其集聚成本超过了集聚效益，由人口过度集聚带来的交通、住房、城市垃圾处理和公共服务供不应求的成本日益增大，因此需要适度限制人口。

本研究在我国城市群最优人口规模以及人口空间结构优化的结合方面做了一定探索，也得出一些有价值的结论。但是在如何协调城市群人口空间格局和城市最优人口规模之间还存在一定理论方面，甚至定量研究的探讨空间。另外，关于齐普夫指数等于1是否符合城市群整体效率最优的问题，也需要进一步探讨，这些将在今后的研究中继续完善。