线性元有限体积元法的一种并行格式

钱 皓, 吴 丹, 吕俊良

(吉林大学 数学学院, 长春 130012)

为提高计算效率, 充分利用机器资源, 设计适合并行化的计算策略已成为计算数学领域内的重要课题.在求解偏微分方程的数值方法上, 目前对差分法和有限体积法的并行化研究已有许多成果[1-5], 其中区域分解方法在格式并行化中具有重要作用, 它将计算区域划分为若干个子区域, 并对子区域进行特殊的界面处理, 将复杂问题转化为若干个子问题, 使构造出的格式有高度并行的特点.有限体积元法作为计算流体力学的常用数值方法, 具有高阶逼近且能自然保持局部守恒性的优点.目前该方法的研究主要包括格式的稳定性分析[6-8]和收敛性分析[9-11]等.此外, 目前在有限体积元法并行化研究方面也取得了一些成果, 其中文献[12]在四边形网格上提出了双线性元有限体积的并行格式和保正修正后的并行格式.本文采用文献[12]中的区域分解思想, 通过预估校正方法, 在随机三角形网格上构造一种非条件稳定的线性元有限体积并行格式, 并用数值算例验证该并行格式的收敛性和并行效率.

1 标准有限体积法

1.1 模型问题

考虑扩散问题

(1)

其中Ω是一个带有边界∂Ω的二维多边形区域,X=(x,y)T∈2,f(X,t)为源项,g(X,t)为边界条件,φ(X)为初值条件,κ=(kij(x,y))2×2∈2×2为扩散张量.假设系数矩阵κ对称且有一致的上下界, 即存在常数0<γ1<γ2, 使得γ1(ξ,ξ)≤(κξ,ξ)≤γ2(ξ,ξ)对任意实向量ξ∈2和都成立.并设函数f(X,t),g(X,t),φ(X)充分光滑.

1.2 网格剖分与函数空间

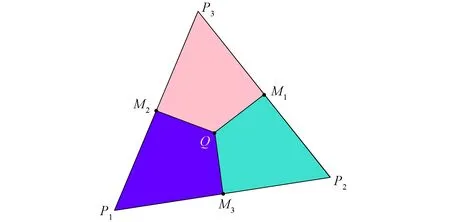
图1 三角形单元△P1P2P3的对偶剖分Fig.1 Dual partition of triangular unit △P1P2P3

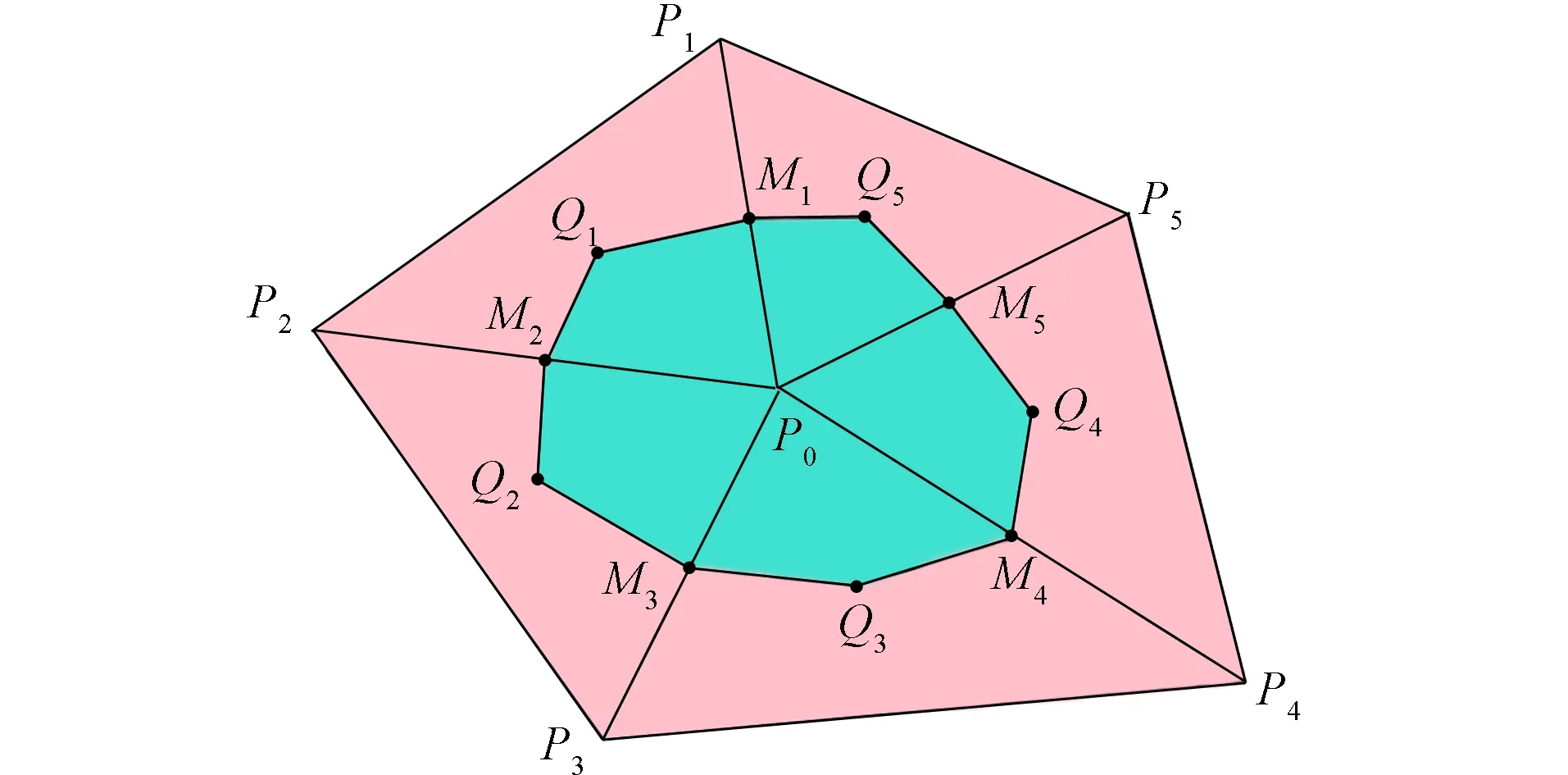
图2 顶点P0所在的对偶单元Fig.2 Dual unit of vertex P0

对于给定的t∈[0,T], 取试探函数空间为

其中P1(K)表示在单元K上的一次多项式集合,uh(X,t)|K由K的3个顶点在t时刻的函数值唯一确定.取检验函数空间Vh为相应于对偶剖分的分片常数空间, 即

其中P0(K)表示在单元K*上的常数多项式集合.事实上, 对于每个vh∈Vh, 均可唯一地表示为

1.3 有限体积元离散格式

(2)

成立, 其中

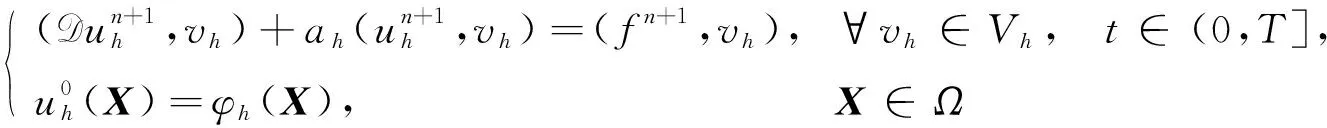
(3)

成立, 其中

2 线性元有限体积并行格式

2.1 区域分解

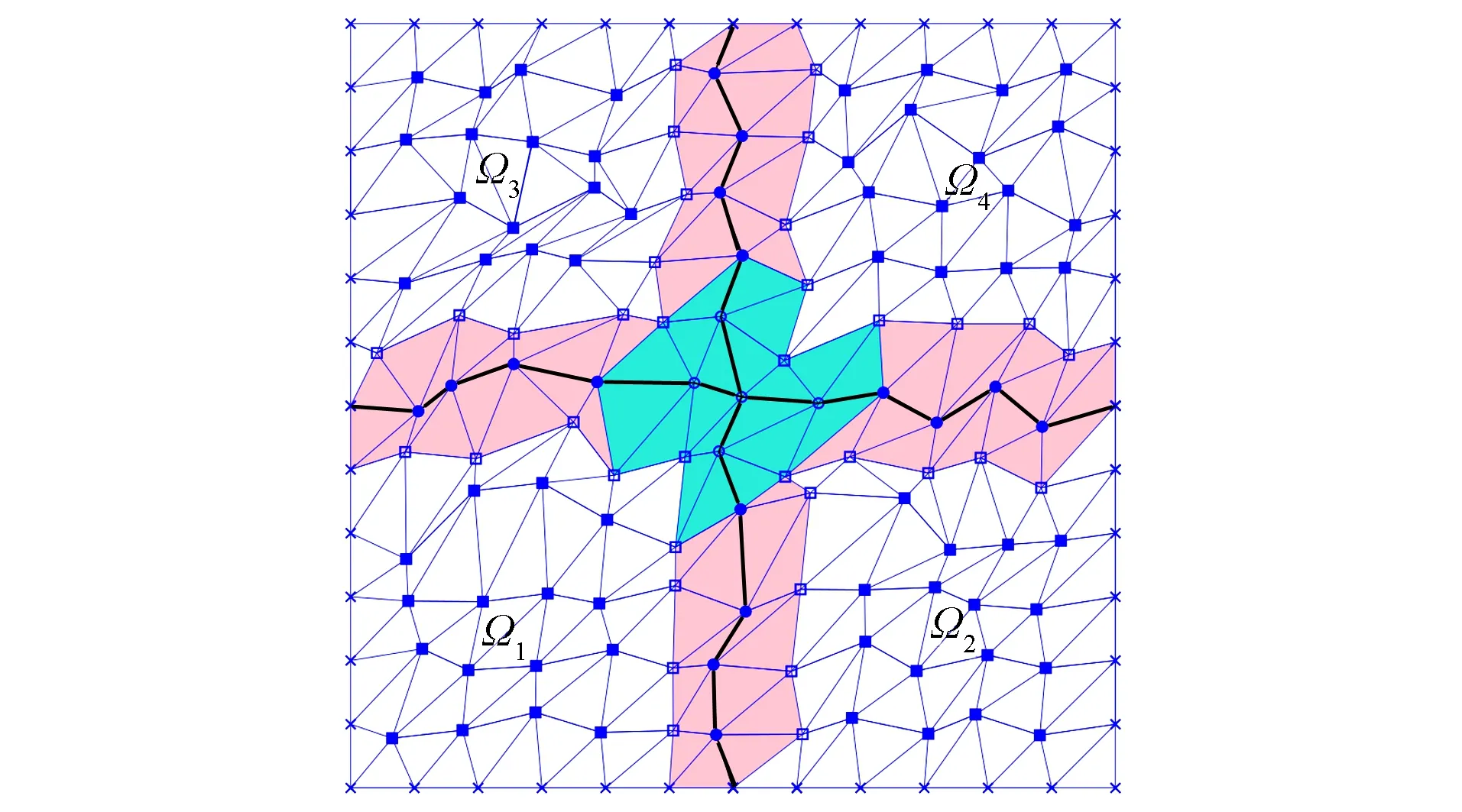
图3 分成4个并行子区域时的节点Fig.3 Nodes when domain is divided into 4 parallel sub domains

将区域Ω分成R个子区域Ωi(i=1,2,…,R), 用○和●表示两个相邻子区域之间界面上的网格节点, □和■表示子区域内部的网格节点,×表示∂Ω上的网格节点.由不同子区域共享的子边界称为区域分解的交界面, 不妨设有K个, 用Bk表示第k(k=1,2,…,K)个交界面上节点的集合.同时位于多个交界面上的节点称为区域分解的交点, 记作Oj(j=1,2,…,J).图3为Ω被分成4个子区域Ωi(i=1,2,3,4)时的节点分布情况.

2.2 并行算法

算法1线性元有限体积并行算法.

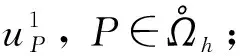
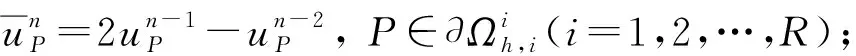
注1本文利用前两个时间层上子区域交界面处的值, 采用算术平均意义下的线性外推方法, 对子区域交界面处的值进行预估, 将复杂问题转化成了若干个Dirichlet边值子问题进行并行求解；再利用求出的值对交界面进行修正.故对于每个子进程, 其所需保存的数据为前两个时间层上子区域交界面处的值与前一个时间层上子区域内部的值.

3 数值实验

下面用一些数值算例检验线性元有限体积并行格式的收敛性与并行效率.引入L2,H1和L∞的范数:

定义格式的收敛阶为

(4)

其中h1,h2表示网格的尺度,δ(h1),δ(h2)表示该网格单元数下的误差.为测试格式的并行效率, 定义计算公式:

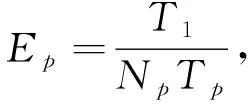
(5)

其中Np为并行程序所用的核数,T1为算法串行花费的时间,Tp为使用p核并行算法花费的时间.令τ=T/N, 则网比μ=τ/h2.

本文采用Fortran编译语言, 并使用MPICH2的函数库, 通过MPI通讯方式实现程序的并行.数值实验在北京超级云计算中心M分区(BSCC-M)上进行, 本地环境为Windows10, 运行环境为Linux-CentOS7, 单个计算节点的处理器为512 GB内存, 128核的AMD EPYC CPU.为达到并行的效果, 本文对每个子区域都采用单独一个核进行运算, 因此程序所需的核数等于子区域的数量.在求解程序中的线性方程组时, 本文采用GMRES(m)迭代算法, 迭代终止值为10-16.

例1各向同性扩散问题.

将计算区域分为16个子区域, 设起始时刻为0, 终止时刻为0.1 s, 网比为5, 分别计算如图4所示的摄动网格Ⅰ和如图5所示的Sine网格上解的误差, 得到其计算精度, 分别如图6和图7所示.设起始时刻为0, 终止时刻为0.001 s, 时间剖分数为1 000, 网格尺寸为1/1 000, 固定一个摄动网格Ⅰ, 记录不同并行区域数时并行格式所需的计算时间, 并计算并行效率, 结果列于表1.实验结果表明, 对于各向同性扩散问题, 并行格式的数值解按L2模2阶收敛, 按H1模1阶收敛, 按L∞模2阶收敛, 且具有良好的并行效率.

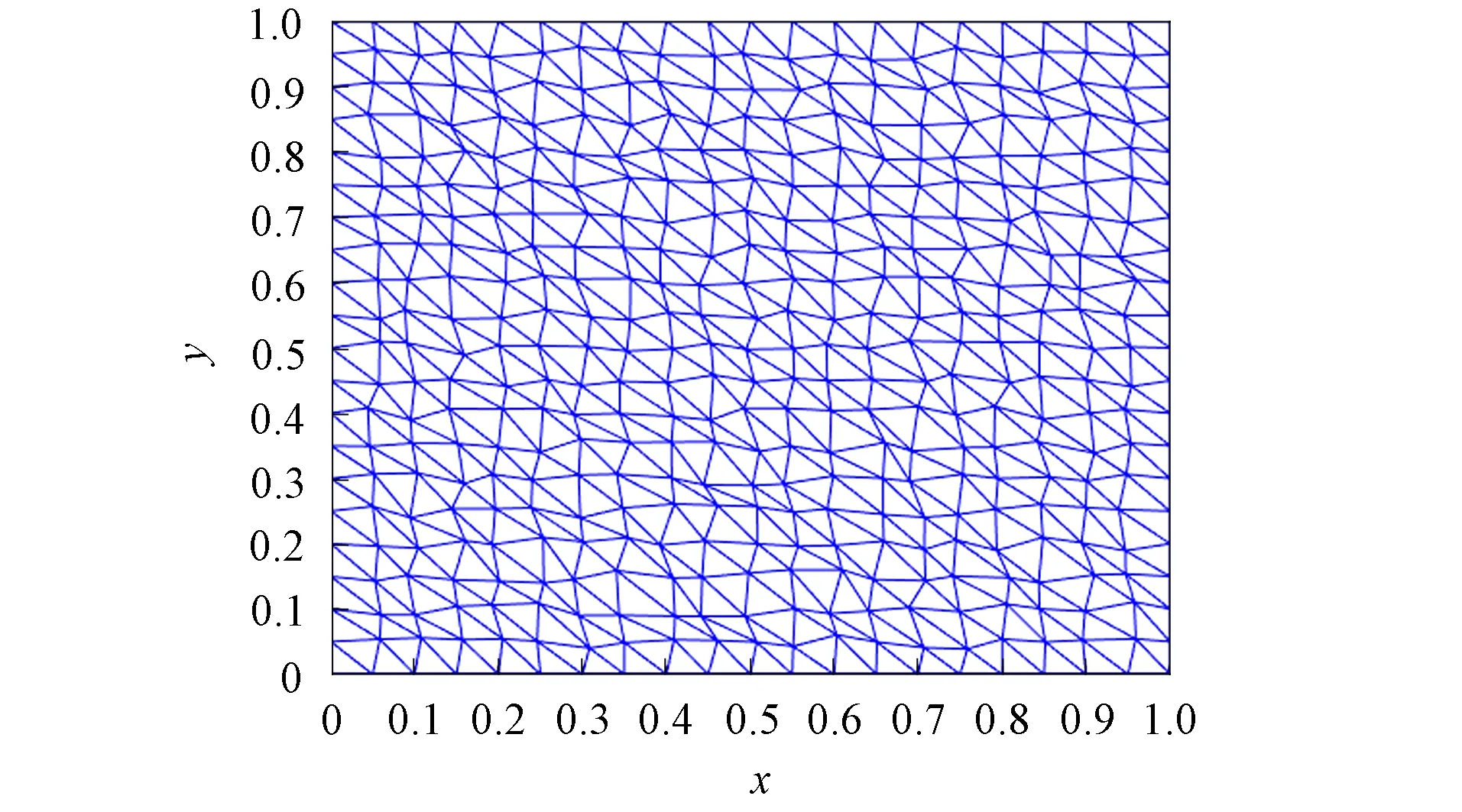
图4 摄动三角形网格ⅠFig.4 Distorted trianglar mesh Ⅰ

图5 Sine三角形网格Fig.5 Sine trianglar mesh

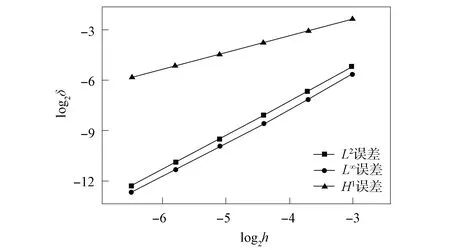
图6 摄动网格Ⅰ上的计算精度Fig.6 Computational accuracy on distorted mesh Ⅰ

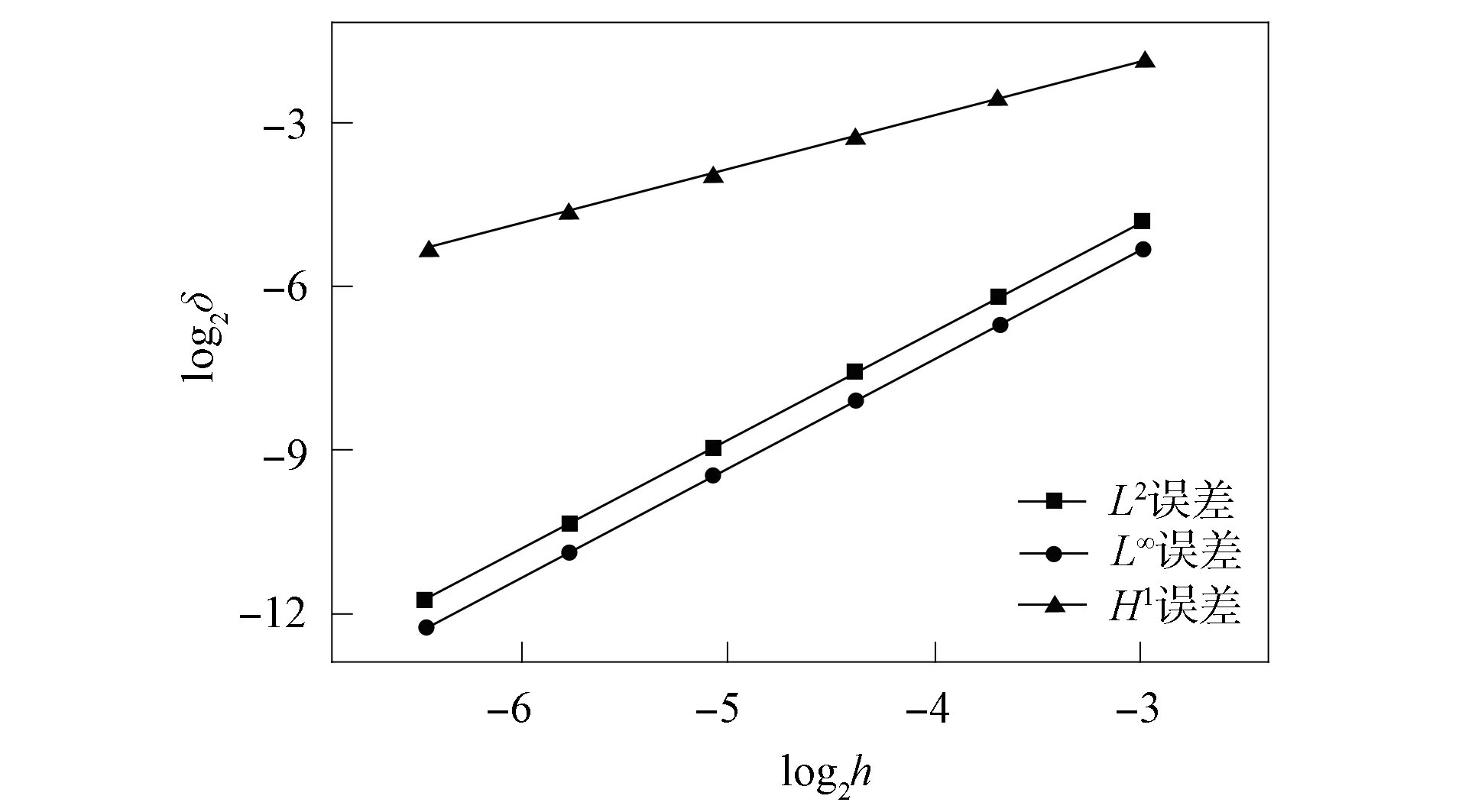
图7 Sine三角形网格上的计算精度Fig.7 Computational accuracy on Sine trianglar mesh

表1 摄动网格Ⅰ上的并行效率(T=0.001, N=1 000)

例2各向异性扩散问题.

考虑各向异性的扩散方程(1), 其扩散系数为

其中α为可变参数, 方程的精确解为u(x,y,t)=e-π2tsin(πx)sin(πy).

图8 当α=10-6时的计算精度Fig.8 Computational accuracy when α=10-6

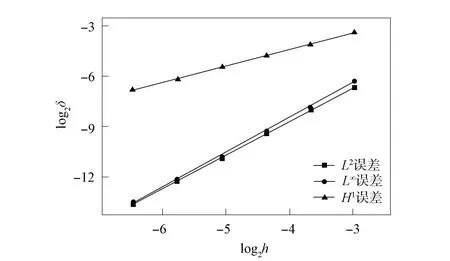
图9 当α=102时的计算精度Fig.9 Computational accuracy when α=102

将区域分为16个子区域, 设起始时刻为0, 终止时刻为0.2 s, 网比μ=1, 分别取α为10-6和102, 采用线性元有限体积并行格式, 计算摄动网格Ⅰ上数值解的误差, 结果分别如图8和图9所示.设起始时刻为0, 终止时刻为0.001 s, 时间剖分数为1 000, 网格尺寸为1/1 000,α=10-2, 计算在同一个摄动网格Ⅰ上使用不同核数时, 格式的并行效率, 结果列于表2.实验结果表明, 对于各向异性的扩散问题, 该并行格式能达到最佳收敛, 且并行效率达到0.7以上.

表2 α=10-2时的并行效率(T=0.001, N=1 000)

例3间断的扩散系数问题.

考虑带有非连续扩散系数的抛物方程(1), 其扩散系数为

方程的精确解为

将区域分为9个子区域, 设起始时刻为0, 终止时刻为0.01 s, 网比为1, 分别计算如图10所示的摄动网格Ⅱ和如图11所示的梯形网格上数值解的误差, 得到其计算精度，分别如图12和图13所示.设起始时刻为0, 终止时刻为0.001 s, 时间剖分数为N=1 000, 网格尺寸为1/900, 用线性元有限体积并行格式, 在梯形网格上计算不同核数时的并行效率, 结果列于表3.实验结果表明, 对于间断的扩散问题, 该并行格式的误差也能达到最佳收敛阶, 且并行效率良好.

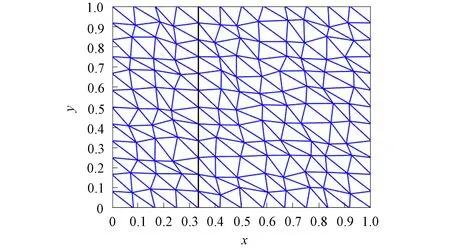
图10 摄动网格ⅡFig.10 Distorted mesh Ⅱ

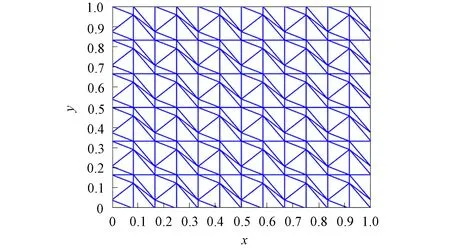
图11 梯形网格Fig.11 Trapezoidal mesh

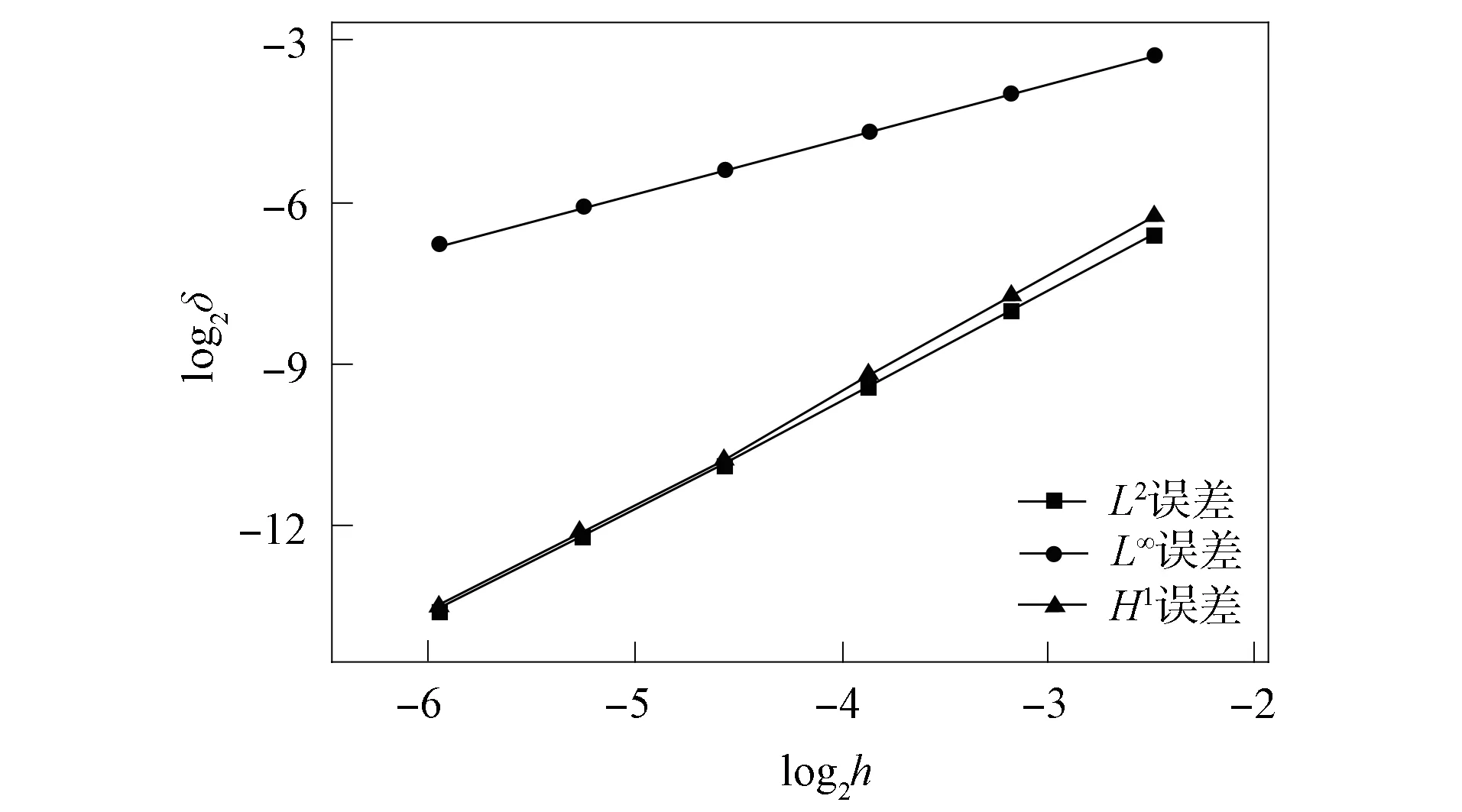
图12 摄动网格Ⅱ上的计算精度Fig.12 Computational accuracy on distorted mesh Ⅱ

图13 梯形网格上的计算精度Fig.13 Computational accuracy on trapezoidal mesh

表3 梯形网格上的并行效率(T=0.001, N=1 000)

综上所述, 本文从微分方程的数值格式出发, 在扭曲的三角形网格上, 提出了一种适用于在多核机器上运算的线性元有限体积并行格式.该格式采用预估校正技术实现了其可并行性.为不失去原有格式的收敛性, 本文在子区域交界面上采用了前两个时间层上值的线性外推方法进行预估.该并行格式只需在相邻的子区域之间进行数据的通讯, 且只有区域交界面周围的点参加了通讯, 故不会产生大量的时间消耗.数值实例结果表明, 本文格式不仅可极大减少计算时间, 而且能保持原有的收敛速度.