液压机自适应鲁棒运动控制

杨清华

(江苏城市职业学院,江苏 常州 213001)

1.引言

液压机常用于塑性材料的压制加工工艺,如冲压、弯曲、翻边、薄板拉伸等,也可用于校正、压装、塑料及粉末制品的压制成型工艺。液压机可以在一定范围内任意改变加压的压力及各个行程的速度,能很好地满足各种压力加工工艺的要求。[1]液压机的电液控制系统在工作阶段存在参数不确定性、非线性环节和外界干扰等问题,[2]因此实现液压机精确的轨迹跟踪控制以提高其工作性能是当前的研究热点。此外由于液压元件的磨损,系统具有高度时变性,而液压机在工作过程中受到的负载干扰力也是相当大的,如果没有得到适当的补偿,系统很容易失稳。本文设计了两种自适应律,外环自适应律不仅负责补偿压制阶段产生的外力,还负责补偿作用于机械子系统的所有未建模的因素,如摩擦、压力供应系统的非理想性和流体可压缩性等。第二个自适应律用于减少由于部件的磨损而导致的系统性能下降,因为磨损主要影响就是导致跟踪误差和系统失稳。另一个主要问题是由于部件间磨损效应,位置误差会随时间而增加,这不仅导致生产性能下降,还经常导致机器为了重新校准控制器而发生的生产中断,生产效率下降。此外,系统没有关于液压元件健康状况的信息,给预测性的维护造成了困难。

由于现代社会对产品质量的要求日益提高,液压机控制系统的要求也随之提升,要求是瞬态最大跟踪误差为0.5mm,瞬态相位和最大稳态误差要低一个数量级。此外,最大超调量必须低于1%。这种严格的要求,加上前面提到的电液系统的非线性,宜采用非线性自适应控制系统以确保在标准工况以及在不确定的条件下,当存在外力和部件磨损时系统的工作性能。本文将采用内外环控制策略,[3]外环负责控制液压机的运动,施加在活塞上的力作为控制输入,而内环则负责补偿伺服阀的泄漏量。

2.系统描述

本文中的液压机有8个同步移动的轴。即使在尺寸、最大速度和产生的压力上都有所不同,但所有的轴都具有相似结构,如图1所示。这里重点研究一个特定的轴，其主要组成部分包括：单向定量液压泵,负责提供28MPa的工作压力、两组单杆活塞式液压缸、三位四通电液伺服阀,用来控制活塞的运动方向。本文的主要任务是识别和补偿液压回路中的泄漏。产生泄漏的主要部件是活塞和控制阀。一般来说,泄漏量取决于系统的环境条件及其系统的工作时间,因此很难建模。泄露量随机出现在系统中的小孔口且具有时变性,在本文液压系统中,泄漏主要出现在液压缸和控制阀中,在液压缸中,泄漏现象可分为内部泄漏和外部泄露两种,[4]内部泄漏是由于活塞与缸体的密封圈磨损导致的两个腔之间的油液非正常流动,而外部泄露是由于液压缸端盖或活塞杆的密封损坏导致油液直接外泄出液压缸。本文只考虑内部泄露。控制阀的泄漏量的考虑因素与液压缸类似,本文暂不考虑。

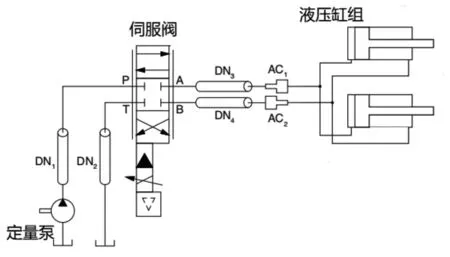
图1 液压系统原理图

3.控制模型的建立

根据系统的组成以及本文第2部分所讨论的内容,建立研究的液压支路控制系统的数学模型。此支路有两个并联同步运动的液压缸和一个三位四通电液换向阀,为了简化,这里只研究一个液压缸即可。建立数学模型如下[5]：

⑴

其中：x1(t)，x2(t)，m分别是液压缸的位移和速度以及活塞质量；

Cv是粘性摩擦系数；

Ff(x2(t))考虑了未建模的摩擦效应，Ff未知但它是连续的Lipschitz函数；

d(t)是作用在活塞上的未知的外部干扰力；

A1和A2分别是液压缸上下两腔的油液作用面积；

x3(t)和x4(t)分别为液压缸上下两腔的油液压力；

βe是油液的体积模量；

V1(x1(t))和V2(x1(t))分别对应液压缸两个腔的体积；

u(t)是阀芯的滑移位移；

ql(t)为未知的内部泄漏量；

Q1(x3(t),u(t))和Q2(x4(t),u(t))分别为液压缸两个腔的输入流量和输出流量。

在(1)中，控制输入是阀芯的滑移位移。由于阀具有不对称性，流量Q1Q2显然不对称。Q1可以表示成：

⑵

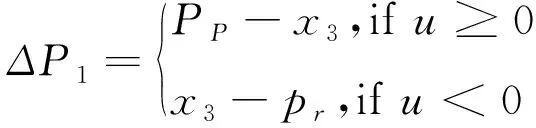
PP为系统的供应压力，本文中系统的供应压力为28MPa，Pr=0MPa为环境参考压力。C01是伺服阀的流量增益。同样地，Q2可以这样表示：

⑶

4.控制器设计

本章的主要内容是设计一个鲁棒自适应控制系统，这个系统能动态地应对压力机在压制过程中的高幅度外部干扰d(t)，也能够补偿缓慢变化的内部泄漏效应ql(t)，也能满足诊断和维护的需要。 综合(1) ，(2) 和 (3) ，该装置可描述为：

⑷

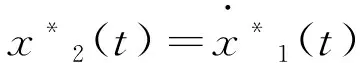
·参数Cv，C01，C02，m，βe，A1，A2，V01和V02是已知的常数；

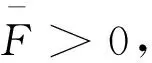
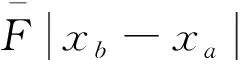
⑸

且对于任意的x*2(t)，有

⑹

这里Φix*2(t)是已知的有界函数，而φi是实常数， 其中i=1,...,Nf

·对于任意的参考轨迹x*1(t)都存在一组已知的有界函数Γi(t)，一组未知的参数Υi,i=1,...,Nd，以及一个已知的有界函数Fext(x1)，存在以下关系：

d(t)=Fext(x1(t))+dΥ(t)

⑺

其中：

⑻

·对于内部泄漏，我们认为：

C0l是一个未知孔的泄漏流量增益系数，而xl(t)是小孔截面积，以上两个参数都是未知，所以可以写为：

ql(t)=gl(t)Gl(x3(t),x4(t))

⑼

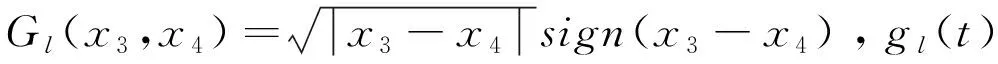
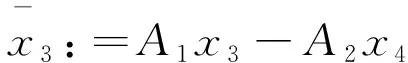
⑽

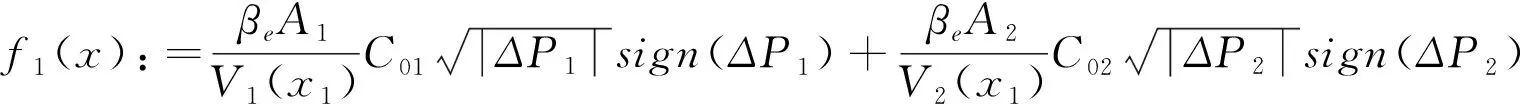
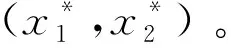
⑾

⑿

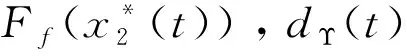
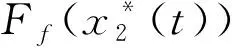
⒀

命题2：考虑到系统(11)中的Ff(x2)满足式(6)，dΥ(t)在公式(7)中被定义，以及(13)的Θ(t)，当命题1成立，设θ:=(φ1,...,φNf,Υ1,...,ΥNd)T,则由(11)得到闭环控制系统的轨迹，控制动作为:

⒁

自适应率为：

⒂

它是有界的，且(z1(t),z2(t),ξθ(t))是有界全局地、均匀地，指数地收敛于(0,0，-θ)。(15)中ξθ∈Nf+Nd，Kθ是个(Nf+Nd)×(Nf+Nd)是一个对称正定实矩阵。(14)中的K1和K2是正增益。我们得到：

这里;

⒃

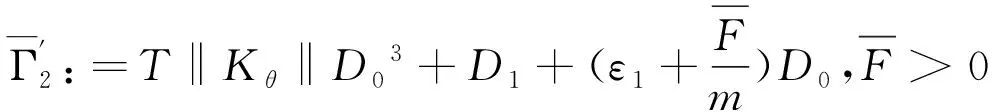
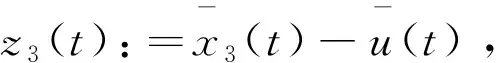
⒄

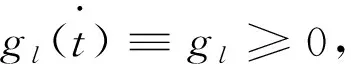
命题4：考虑式(17)的Ff(x2)满足条件，另外认为命题1和命题3 都是正确的。则由公式 (17) 产生的闭环系统运动轨迹的控制作用可以写为：

⒅

从而得到自适应律：

⒆

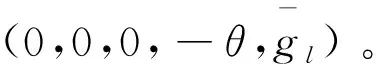
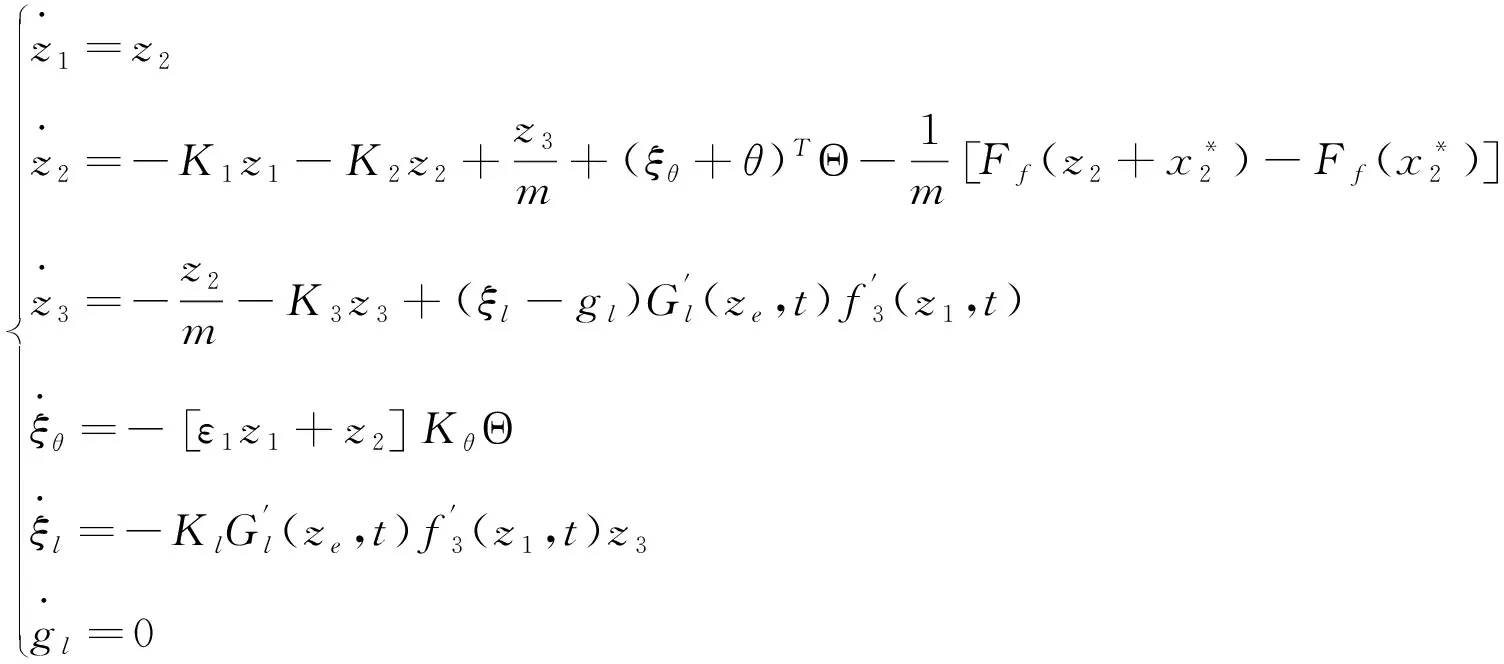
⒇

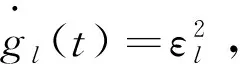
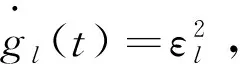
5.仿真

在本节中，对压力机进行了物理建模，[9]介绍了一些仿真结果。特别介绍了命题4中完整控制方案的性能，不仅在外力补偿方面(如图2所示),而且在液压系统存在泄漏的情况下。活塞经历了多个工作循环，同时将未知的外力施加于活塞，并在滑阀命令中添加一个未知的偏移量，以模拟阀门中的泄漏，该命令生成图4中红色的泄漏开口曲线。因为力和泄漏自适应回路都能够补偿外部干扰，本控制器具有相当好的性能。如图3所示，位置和速度跟踪误差保持与无泄漏时相同的大小。更准确地分析一下，最大位置跟踪误差这里等于0.41 mm，最大速度跟踪误差为66.71 mm/s。另一方面，泄漏开口的估计特征图由图4表示。值得指出的是在现实工况中，泄漏动态比这里模拟的要慢得多，这种水平的内部泄漏在几十万次循环后才能达到，通常当泄漏强度达到1-1.5mm开口时就应该更换阀门了。在任何情况下，自适应回路都能够正确估计泄漏，并将这些信息成功应用于控制回路，使系统即使在一些极端的情况下，性能也是可以接受的。估计泄漏中的波动是由于泄漏的自适应控制回路也受到压机工作周期中产生的力的影响，换句话说，负责估计和补偿的自适应回路的增益大于现实中所需要的值。

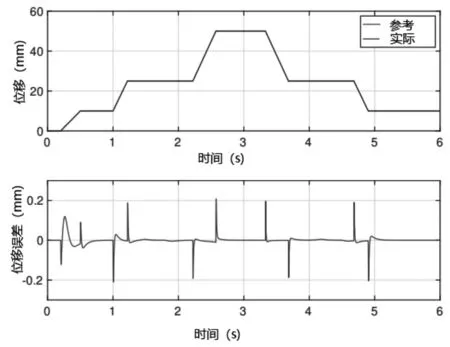
图2 一个工作循环的活塞运动轨迹(有外力作用，无泄漏)

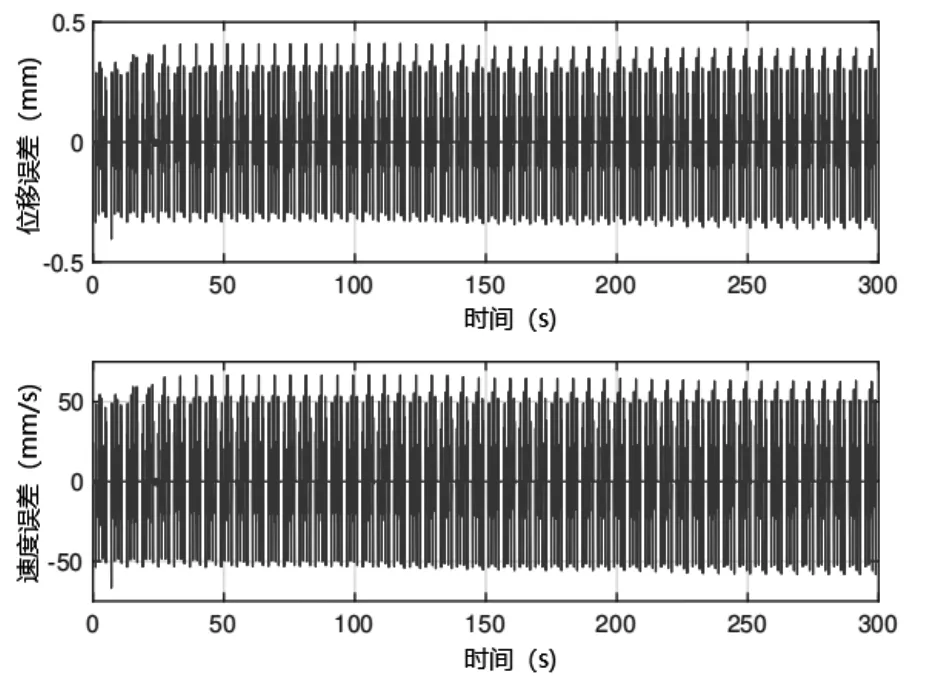
图3 多个工作循环的活塞位移和速度误差(有外力作用，无泄漏)

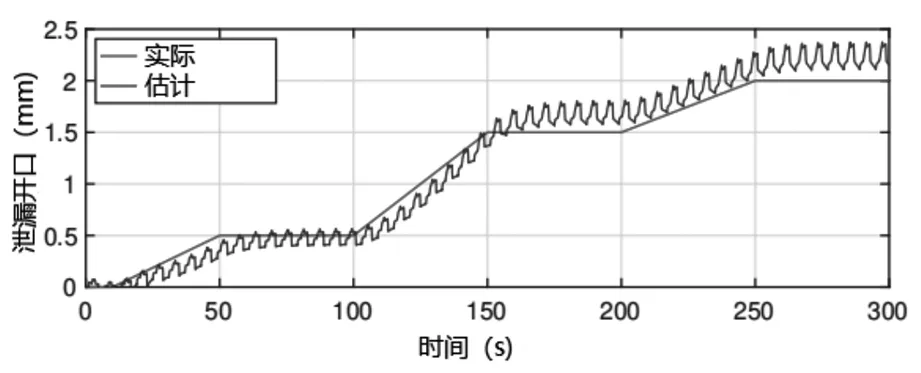
图4 多个工作循环的泄漏开口及其估计值

6.结论

本文提出了一种液压机的自适应鲁棒控制方法。该设计是基于经典的反推参数算法，并由此产生的控制规律具有内外环结构。在此方案的基础上，设计了两种自适应律，外环的自适应律不仅负责补偿压制阶段产生的外力，还负责补偿作用于机械子系统的所有未建模的因素，如摩擦、压力供应系统的非理想性和流体可压缩性等。第二个自适应律用于减少由于部件的磨损而导致的系统性能下降，因为磨损主要影响就是产生伺服阀的泄漏量。通过建立系统的物理模型并进行仿真，证明了该控制方案的有效性和闭环稳定性。