装配工况下PEMFC 不同双极板截面接触行为研究
2023-03-08任立海杨振华李盛蒋成约赵清江
任立海 ,杨振华 ,李盛 ,蒋成约 †,赵清江
(1.汽车噪声振动和安全技术国家重点实验室,重庆 401122;2.中国汽车工程研究院股份有限公司 博士后工作站,重庆 401122;3.重庆理工大学 汽车零部件先进制造技术教育部重点实验室,重庆 400054)
质子交换膜燃料电池(Proton Exchange Mem⁃brane Fuel Cell,PEMFC)电堆以其高功率密度、快速启动能力、较低的工作温度和零排放等优点被广泛认为是可以在多领域应用的潜在替代能源[1-2].双极板作为PEMFC 电堆的核心组成部件之一,在电堆工作过程中起到支撑、为冷却液和反应气体提供流道、收集与传导电流等作用,其物理特性对电堆的工作性能有着较大的影响[3].合理的双极板流场几何参数可以优化双极板物理特性、改善电堆的工作性能、实现电堆系统运行成本的大幅下降[4-5].
双极板的流场设计大致可以分为流场结构设计、截面形状设计和截面几何参数选择等三个方面[6].其中,双极板的流场结构决定了反应气体和冷却水的流动状态,通过优化流场结构可以提高反应气体的传输效率和改善燃料电池的水热管理[7].Shimpalee 等人的研究表明改变流场结构和通道特性会影响PEMFC 电堆的性能和气体均匀性分配[8].考虑PEMFC 电堆的实际使用要求,选择合适的流场结构,可以最大限度地提高电堆的工作性能[2].对于双极板截面几何参数的研究大多从流道宽度、肋宽度和流道高度入手,由此来分析选择不同的参数对PEMFC 电堆性能的影响[9].Chiu 等人发现可以通过减小流道高度或宽度来改善平行流场和蛇形流场的电堆性能,并且当通道纵横比接近于1 时,可以通过减小通道尺寸来改善平行流场和蛇形流场的除水性能和电堆性能[10].Kim 等人的研究表明在双极板设计中,采用较高的通道和肋宽比会导致GDL(Gas Diffu⁃sion Layer,GDL)在肋上方产生较大的变形,同时在流道沿线产生较高的流动阻力[11].已有关于双极板流场几何特征的研究多集中于流场设计和截面几何参数分析,而双极板截面形状也会对PEMFC 电堆的性能产生较大的影响[6].因此,为了更好地厘清双极板结构设计要素,亟需探究双极板截面形状对PEMFC电堆性能的影响机制.
近年来,研究人员从不同角度开展了关于双极板截面形状对PEMFC 电堆性能影响机制的有益探索.Kumar等人从气体流动性和电化学反应的角度开展研究,结果表明,在其他条件一定时,采用三角形和半球形截面形状双极板可以提高9 %的氢消耗量,这将在一定程度上提高PEMFC 电堆的工作性能[9].Ahmed 等人从电化学反应的角度出发,搭建了不同截面形状的双极板有限元模型,研究表明矩形截面的双极板可以提供更高的电压,而梯形截面的双极板促进了反应物的扩散,从而使反应物和反应区域的局部电流密度更加均匀[12].当前,有关双极板截面形状的研究大多从气体流动性和电化学等角度考虑,少有关于双极板截面形状对双极板与GDL 层间接触行为影响的研究.然而,在电堆装配载荷作用下,双极板与GDL 之间会产生接触应力以及GDL 向气体流道侵入等层间接触行为,从而影响PEMFC 电堆的性能[11,13].因此,如何优化双极板的物理特性、提高PEMFC 电堆的性能,是非常具有工程实际价值和研究意义的.
本研究选用金属双极板作为研究对象,旨在探索装配载荷作用下PEMFC 电堆双极板截面形状对双极板与GDL 层间接触行为的影响.运用有限元建模仿真方法,构建具有不同截面形状的双极板及相应的双极板压缩试验模型,研究在不同装配载荷作用下双极板截面形状变化对GDL 表面接触应力和GDL 侵入等层间接触行为的影响,以期为电堆整机及零部件的结构设计及工程应用提供参考.
1 方法
1.1 双极板压缩试验
研究搭建了双极板压缩试验台,运用电子万能试验机模拟并施加装配载荷,提取并分析双极板与GDL 之间的接触应力大小和分布情况,为后续验证双极板压缩试验有限元模型的有效性做准备.
1.1.1 试验样件
试验样件由端板、双极板、GDL 及压敏纸等四部分组成.如图1 所示,双极板选用某公司生产的SS316L 金属双极板(不含涂层),双极板流场为波浪形,截面形状为梯形[5].双极板全尺寸为447 mm×143 mm,厚度为0.1 mm,其中活化(流道)区域尺寸为260 mm×113.5 mm.

图1 双极板制备Fig.1 Preparation of bipolar plate
基于本文研究目的,同时为了降低试验误差,利用线切割法制备尺寸大小为100 mm×113.5 mm 的活化区域作为试验样件以替代原金属双极板,如图1(a)所示,截取的活化区域共包含51 条流道.GDL 则选用日本东丽公司生产的TGP-H-060 型碳纸,厚度为0.19 mm,将GDL 裁剪成100 mm×115 mm 的尺寸大小,使得GDL 可以与双极板的每条肋产生接触[14].端板采用不锈钢材料,其尺寸略大于GDL的尺寸;其厚度取30 mm,以防止试验过程中端板发生弯曲变形影响试验结果.压敏纸采用富士公司生产的LLW 型压敏纸,裁剪成与GDL 相同的尺寸,便于完整采集接触应力分布[14].各个试验样件的具体尺寸如表1所列.

表1 试验样件参数Tab.1 The parameters of test samples
1.1.2 试验设置及加载
通过搭建双极板压缩试验台来完成压缩试验:考虑到与GDL 和双极板肋之间的垂直位移相比,质子交换膜与催化剂层之间的位移和质子交换膜与GDL 之间的位移可忽略不计;因此,双极板压缩试验台由电子万能试验机、端板、双极板、压敏纸和GDL组成,不包括质子交换膜和催化剂层[15].电子万能试验机装配力传感器和位移传感器,可以控制试验加载力的大小和加载速度.压敏纸摆放在双极板与碳纸中间,其接触应力采集范围在0.5~2.5 MPa 之间.随着试验机施加载荷的增加,白色压敏纸薄膜逐渐变红,待试验结束后,薄膜上呈现出完整的双极板流道轮廓,轮廓颜色的深浅代表接触应力幅值的高低[14,16-17].搭建好的压缩试验台如图2 所示,下端板摆放在试验机下压头的正上方,从下往上依次摆放碳纸、压敏纸、双极板和上端板,要求各样件居中对齐.

图2 压缩试验台Fig.2 The setup of compression test
压缩试验台搭建完毕后,通过计算机控制电子万能试验机对端板加载.由于0.7 MPa 接近于PEMFC 电堆实际装配载荷,因此研究选用0.7 MPa作为试验机加载载荷[14].考虑试验机是通过施加力的方式加载,将0.7 MPa 装配载荷转换成7 945 N 的压缩力,并通过位移控制使电子万能试验机以1 mm/min的速度对上端板进行准静态加载[14];当试验机施加的力达到预定载荷后,按照压敏纸使用要求保持2 min以充分完成接触应力采集.
1.1.3 试验结果提取
压缩试验结束后将压敏纸取出,进行拍照记录.根据厂家提供的比色卡拟合曲线自主编写MATLAB程序.如图3 所示,运行MATLAB 程序读取试验结果;然后,将彩色图像文件转化为灰度图;根据试验环境的温度、湿度条件进行插值,进一步将灰度值转化为应力值.通过人工核对比色卡浓度值和MATLAB 程序生成的应力云图来验证自主编写程序的准确性[16-18].
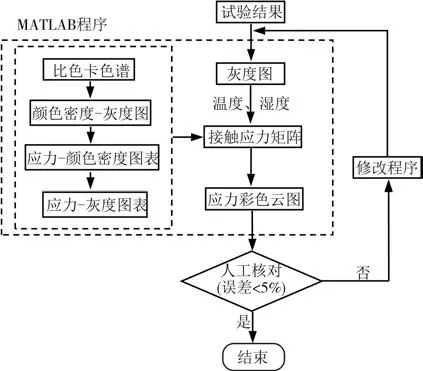
图3 结果提取流程图Fig.3 Schematic diagram of result extraction
1.2 双极板压缩试验仿真
1.2.1 有限元模型建模
如图4(a)所示,参照上述双极板压缩试验,在LS-DYNA 软件环境下构建双极板压缩试验有限元模型.由于端板刚度远大于其他组成,其在试验过程中的变形可以忽略.因此,在有限元模型中,将上端板定义为不可变形刚性材料(*MAT_RIGID),模型尺寸与端板样件保持一致,并采用四节点壳单元对上端板进行网格划分.同时,用刚性墙来模拟下端板.如图4(b)所示,为减少网格数量、提高计算效率,依据某公司提供的双极板图纸和试验截取的流道区域样件,运用四节点壳单元构建双极板有限元模型.为更好地模拟压缩产生的轴向变形,运用六面体实体单元对GDL进行建模.
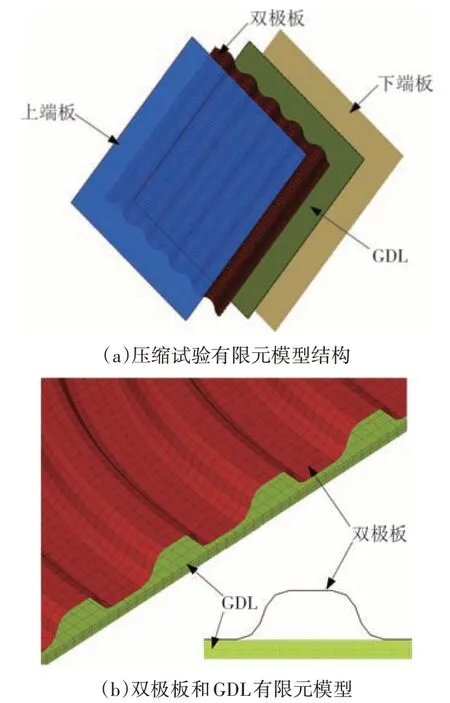
图4 双极板压缩试验有限元模型Fig.4 FE model of bipolar plate compression test
根据双极板和GDL 的材料力学特性,本文选用弹塑性材料本构模型(*MAT_PIECEWISE_LINEAR_PLASTICITY)来模拟其力学行为.该本构模型由屈服前的弹性阶段和屈服后的塑性阶段组成,其中塑性阶段的硬化曲线由多线段组成.该材料可通过填入Cowper-Symonds 本构模型相关参数对材料性能进行设定,其本构方程见式(1).
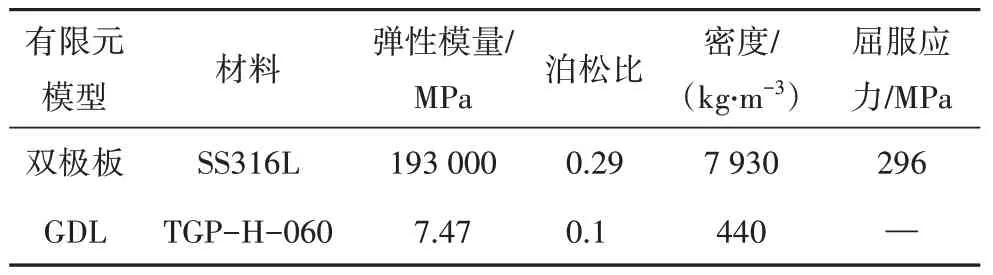
表2 材料参数Tab.2 Material parameters
通过设置关键字对有限元模型加载边界条件,边界条件设置如表3 所示.同时参照双极板的厚度适当调整上下间隙以避免初始穿透.依据试验加载,在LS-DYNA 中对上端板施加0.7 MPa 均布载荷.对试验中准静态载荷的加载速度进行适当的缩放以提高仿真计算的时效性;同时,为避免动态载荷的惯性冲击效应,开展加载速度的收敛性分析,最终确定约1 500倍的缩放系数.

表3 载荷与边界条件Tab.3 Loads and boundary conditions
为平衡仿真精度和计算效率,对搭建好的双极板压缩试验模型开展网格无关性分析.如图5 所示,根据试样结构尺寸特征,分别建立网格边长为 0.4 mm、0.3 mm、0.2 mm和0.1 mm的压缩试验仿真模型,计算在0.7 MPa装配载荷下上下端板间停止距离以评价模型的网格无关性.

图5 网格无关性分析模型Fig.5 FE models for mesh independence analysis
1.2.2 区域误差
考虑到试验所用的双极板存在形状误差,会造成双极板与GDL 产生不良接触,继而对验证结果产生影响,研究选取0.5 MPa 作为试验阈值,筛选去除MATLAB 程序生成的接触应力矩阵中小于0.5 MPa的单元.并进一步将试验结果处理后的接触应力矩阵和仿真计算得到的GDL 应力云图等分成9 个区域,分别计算各区域内单元的平均接触应力,实现对仿真预测精度的区域化评估(图6)[23-24].

图6 区域划分示意图Fig.6 Schematic diagram of divided area
根据下式分别计算各区域试验与仿真的平均接触应力值误差百分比:
式中:σ1为某区域试验平均接触应力值;σ2为对应区域仿真平均接触应力值;ε为平均接触应力误差百 分比.
1.3 不同双极板压缩试验仿真模型搭建
为分析双极板截面形状对双极板与GDL层间接触行为的影响,参考文献数据选取常见的梯形、矩形和波浪形截面形状为研究对象[6],并分别构建压缩试验仿真模型.如图7(a)-(b)所示,选择四个主要的截面几何参数对梯形、矩形双极板截面形状进行设计:流道宽度(w1)、肋宽度(w2)、流道高度(d)和倒圆角(r)[9].在截面设计中,不同截面形状的双极板保持流道高度、流道宽度与肋宽度的和相一致.其中,参考上述试验双极板样件进行梯形截面设计(w1为1.156 mm,w2为0.992 mm,d为0.5 mm,r为0.25 mm);矩形截面的倒圆角r取0.1 mm,其余参数与梯形截面相一致[19];对于波浪形,如图7(c)所示,选取三个尺寸半径R为0.702 mm 的圆弧进行波浪形截面设计.三种截面形状的具体参数如表4所列.

表4 截面几何参数Tab.4 The geometric parameters of section shapes
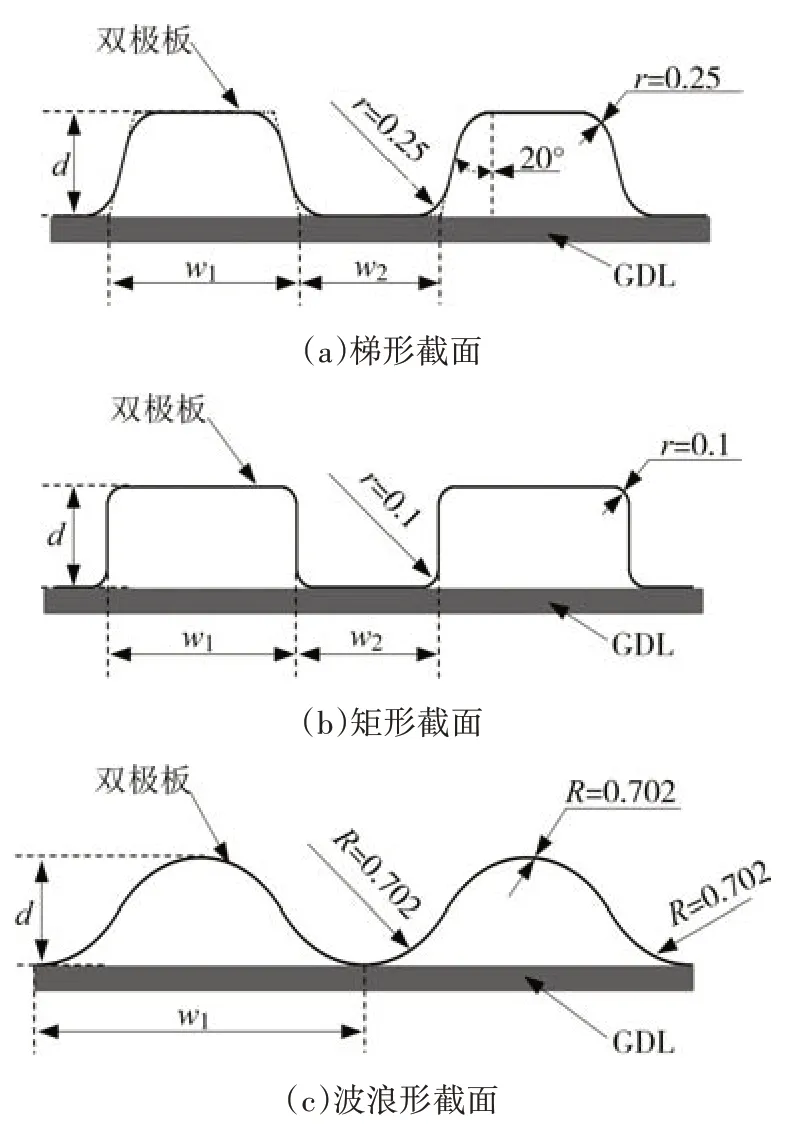
图7 双极板截面形状设计Fig.7 Schematic diagram of section shape design of bipolar plates
为探究双极板截面形状对装配载荷变化的适应性,选用接近于电堆实际装配载荷的0.5 MPa、0.6 MPa 和0.7 MPa 三种载荷,并分别作用于不同截面形状的双极板,共进行9组仿真计算.
1.4 层间接触行为分析
1.4.1 接触应力
为避免损坏GDL 或对PEMFC 电堆性能产生负面影响,需要将与双极板接触的GDL 表面接触应力值限制在一个合适的范围内,同时要保证接触应力的均匀分布[20].因此,研究选用表面整体平均接触应力值和双极板不同肋下平均接触应力标准偏差作为评价GDL 表面接触应力的指标.考虑到双极板肋呈周期性排列,如图8 所示,在双极板左半部分等距选取第1、3、5、…、23、25等13条肋.在与每条肋接触的GDL 表面轮廓区域各选10个单元,求取10个单元的平均值,得到单条肋下GDL表面平均接触应力值.通过计算双极板不同肋下GDL表面平均接触应力的标准偏差来分析双极板下GDL表面接触应力分布的均匀性.接着对13 条肋下的GDL 表面平均接触应力求平均,得到GDL表面整体平均接触应力值.最终利用Excel 2016 软件开展装配载荷和双极板截面形状对GDL 表面整体平均接触应力值影响的双因素方差分析.

图8 单元选取示意图Fig.8 Schematic diagram of element selection
1.4.2 GDL侵入
电堆装配过程中,与双极板直接接触的GDL 会被双极板肋部压紧,非接触区域的GDL 将会被压入流道,从而产生“GDL侵入”.如图9所示,侵入流道的凸起高度h即为GDL 侵入量,凸起的截面积(划线区域)即为GDL 侵入面积[11,25].本研究对三组有限元模型典型区域进行抽样,等间距选取双极板第10、20、30、40、50 共计五条流道.对五条流道内的GDL 侵入面积求平均,得到双极板流道内的GDL 平均侵入面积.通过计算双极板单条流道的截面积,求出GDL侵入面积占流道截面积的百分比,即GDL 平均侵入面积占比.最后利用Excel 2016 软件开展装配载荷和双极板截面形状对GDL 平均侵入面积与GDL 平均侵入面积占比影响的双因素方差分析.
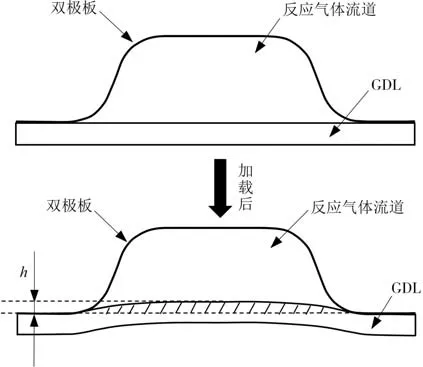
图9 GDL侵入示意图Fig.9 Schematic diagram of GDL intrusion
2 结果与讨论
2.1 网格无关性分析
图10 所示为0.7 MPa 载荷作用下网格无关性仿真分析结果,在所选网格边长变化范围内,仿真计算得到的上下端板停止距离变化误差小于1.13%.因此可以认为网格在所选边长变化范围内具有无关性.由图10 可知:网格越精细,越能够细致地描述压缩过程中GDL 侵入等层间接触行为,但是模型计算时间呈现指数增长(使用超算中心AMD7452CPU@2.35 GHz,64 核进行仿真计算).综合考虑各方面因素,选择0.2 mm作为网格边长基准,双极板压缩试验有限元模型共包含578 154个实体单元和419 152个壳单元.
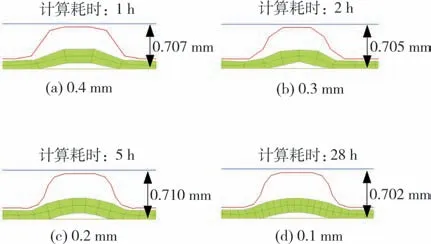
图10 网格无关性分析结果Fig.10 The results of mesh independence analysis
2.2 模型验证
如图11(a)-(c)所示,通过MATLAB程序读取试验结果彩色图像,将压敏纸上的浓度值转换成接触应力值.通过设置阈值对试验结果进行去噪处理,去噪后的接触应力矩阵以云图的形式来展现.
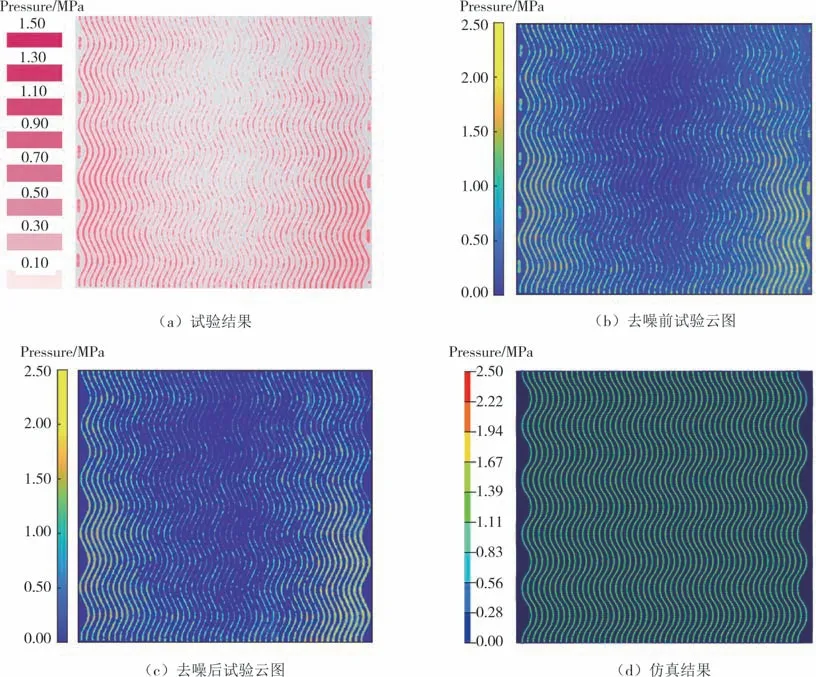
图11 试验与仿真结果展示Fig.11 The results of test and simulation
将压缩试验结果和仿真结果分成9 个区域,分别计算9 个区域的平均接触应力值和平均接触应力误差百分比.通过对比,发现9 个区域误差百分比均在20 %以内,区域1 至8 误差百分比均在15 %以内.各区域的平均接触应力值和平均接触应力误差百分比见表5.
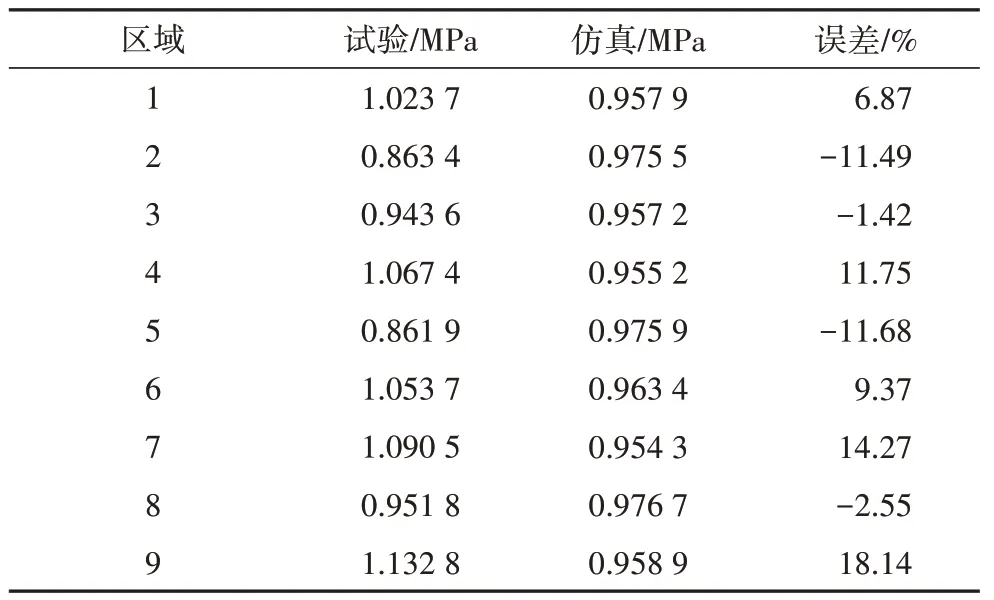
表5 试验与仿真平均接触应力误差Tab.5 Error between the tested and simulated average con⁃tact pressure
为更直观地表示各区域平均接触应力误差百分比大小,如图12所示,结果以九宫格形式表示.
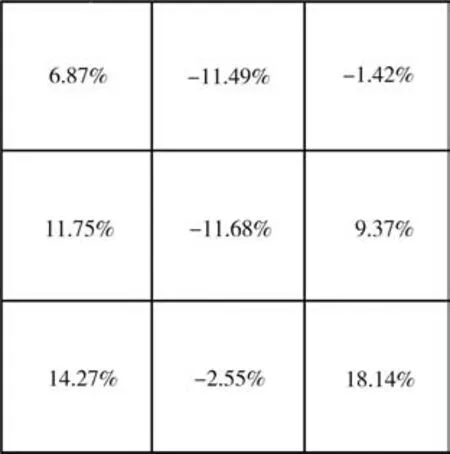
图12 各区域误差Fig.12 Error of each area
结合图11(c)、(d),可以发现试验结果与仿真结果存在一致性,试验结果中心区域接触应力分布与仿真存在差异,但整体差异在可接受范围内.区域9误差较大的原因可能是试验所用端板上下平面加工的平行度不够,存在形状误差;同时装配件在摆放过程中也存在着误差,这会导致试验结果均匀性较差.本研究的验证结果与Lee 等人[24]的研究存在一致性,且误差百分比更低,因此可以认为本研究建立的双极板压缩试验有限元模型是有效的.
2.3 双极板-GDL接触应力
在电堆装配过程中,与双极板接触的GDL 表面接触应力值过大可能会导致GDL 发生损坏,接触应力值过小会出现密封性不足等问题,从而降低PEMFC 电堆的整体性能.根据Zhou 等人的研究,当接触应力小于0.5 MPa时,接触区域被认为是无效接触区域,这将对PEMFC 电堆的性能产生不利的影响[26].而Yi 等人的研究表明,当接触应力达到2 MPa时,双极板肋下的GDL开始出现结构性损坏,GDL表面开始出现纤维断裂[19].为避免类似现象的发生,需要将接触应力值限制在合适范围内.
仿真计算得到三种双极板在0.5 MPa、0.6 MPa和0.7 MPa 装配载荷作用下的接触应力响应.图13给出了在0.7 MPa装配载荷作用下,三种双极板中心区域下GDL 表面接触应力云图.由图13 可以看出,三种双极板下GDL 表面整体平均接触应力值均在0.5~2 MPa之间,因此三种双极板都符合装配要求.

图13 双极板中心区域下GDL表面接触应力云图(0.7 MPa)Fig.13 Contours of the contact pressure of GDL surface beneath the center area of bipolar plate(0.7 MPa)
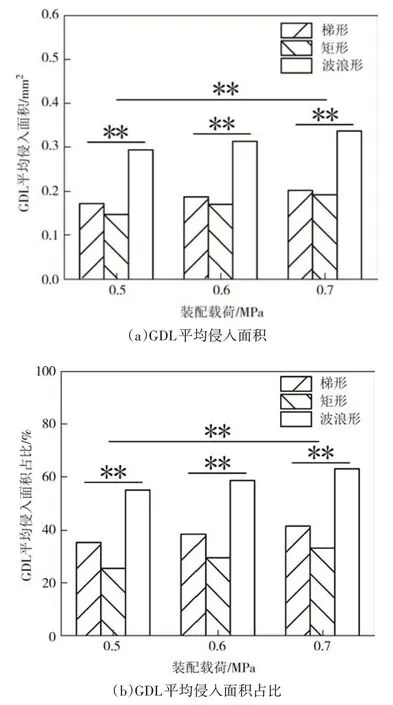
如图14 所示,在相同装配载荷作用下,波浪形双极板下GDL 表面整体平均接触应力值始终最大,而梯形和矩形双极板下GDL表面整体平均接触应力值较为接近.例如,在0.7 MPa装配载荷作用下,波浪形双极板下GDL 表面整体平均接触应力值为 1.25 MPa,梯形与矩形双极板下GDL 表面整体平均接触应力值分别为1.07 MPa、1.01 MPa.这是因为在相同装配载荷作用下,双极板流道长度一定,波浪形双极板肋宽度最小,因此波浪形双极板与GDL 之间的接触面积最小,继而导致波浪形双极板下GDL 表面整体平均接触应力最大.而矩形和梯形双极板的肋宽度相等,因此双极板与GDL接触面积相同,故两种双极板下GDL 表面整体平均接触应力大小相近.由此可知,在同等条件下,双极板肋宽度是决定双极板下GDL 表面整体平均接触应力大小的主要因素.同时,双因素方差分析结果显示,装配载荷和双极板截面形状对GDL表面整体平均接触应力幅值有非常显著的影响.图14 中的*表示影响显著,即0.01 在不同装配载荷作用下,双极板不同肋下GDL表面平均接触应力值的标准偏差以误差棒的形式来表示.从图14 可以看出,在不同载荷作用下,矩形双极板不同肋下GDL表面平均接触应力值的标准偏差最大,这说明矩形双极板与GDL 之间的接触应力分布均匀性始终最差.Nakagaki 等人的研究结果显示,双极板与GDL 之间的接触应力分布越均匀,双极板导电性能越好[25].由此可以看出,在不同装配载荷作用下,矩形双极板与GDL 之间接触应力分布均匀性最差,可能会导致矩形双极板导电性能较差. 图14 GDL表面整体平均接触应力幅值及不同肋下GDL表面平均接触应力的标准偏差Fig.14 Amplitude of overall average contact pressure of GDL surface and standard deviation of average contact pressure of GDL surface beneath different ribs 由表6 可知,随着装配载荷的增加,矩形双极板下GDL 表面整体平均接触应力增长百分比最大,这说明矩形双极板下的GDL表面整体平均接触应力对装配载荷变化的敏感程度高于梯形和波浪形.同时,随着装配载荷的增加,三种双极板下GDL 表面整体平均接触应力增长百分比出现下降的现象.例如,装配载荷增加到0.6 MPa时,矩形双极板下GDL表面整体平均接触应力增长百分比为20.42 %,而当载荷增加到0.7 MPa时,整体平均接触应力增长百分比降到了16.89 %. 表6 双极板下GDL表面整体平均接触应力增长百分比Tab.6 The growth percentage of overall average contact pressure of GDL surface beneath bipolar plate 在装配载荷作用下,双极板肋部与GDL 发生接触,较高的接触应力使得双极板肋下的GDL 发生变形,进而侵入流道内.根据Nakagaki 等人的研究可知,GDL 被压入双极板流道内会产生额外的表面压力,继而造成压力损失[25].Kim 等人的研究表明,当GDL 侵入面积不变时,更小的双极板流道截面积会造成更大的压降,因此较高的GDL 侵入百分比将对PEMFC电堆的性能产生不利影响[11]. 计算求得双极板第10、20、30、40、50 等五条流道内GDL 侵入面积的平均值和流道截面积.图15 给出了三种双极板在不同装配载荷作用下GDL平均侵入面积和GDL平均侵入面积占比.同时,双因素方差分析结果显示,装配载荷和双极板截面形状对GDL平均侵入面积和GDL平均侵入面积占比有非常显著的影响. 图15 GDL侵入结果Fig.15 The results of GDL intrusion 由图15(a)可以看出,在相同装配载荷作用下,波浪形双极板流道内GDL平均侵入面积明显大于矩形和梯形双极板,梯形双极板流道内GDL 平均侵入面积略大于矩形双极板.这是因为波浪形双极板下GDL 表面整体平均接触应力大于矩形和梯形双极板,使得更多的GDL被压入双极板流道内.而矩形和梯形双极板下GDL表面整体平均接触应力值相差不大,因此GDL 侵入流道内的面积相近.由此可见,在同等条件下,双极板肋宽度不仅会影响整体平均接触应力的大小,还会影响GDL 侵入双极板流道内的面积. 由图15(b)可以看出,随着装配载荷的增加,GDL 平均侵入面积占比也增加.在不同装配载荷作用下,波浪形双极板流道内GDL 平均侵入面积占比均超过了50 %,明显大于矩形和梯形双极板.而较高的GDL 侵入占比会对PEMFC 电堆的性能产生不利影响,因此,采用波浪形双极板的电堆在运行过程中,更多的GDL 被压入流道内,会造成较大的GDL平均侵入面积占比,这可能会造成较大的压力损失. 将三种双极板流道内的GDL平均侵入面积对装配载荷的敏感度进行量化.从表7 可以看出,随着装配载荷的增加,矩形双极板流道内GDL 平均侵入面积的增长百分比始终最大.例如,当装配载荷增加到0.6 MPa时,矩形双极板流道内GDL平均侵入面积增长百分比为15.58 %,梯形为8.95 %,波浪形为6.57 %.这说明矩形双极板下的GDL 侵入行为对装配载荷变化的敏感程度高于梯形和波浪形. 同时,由表7 可以看出,随着装配载荷的进一步增加,梯形和矩形双极板流道内GDL 平均侵入面积增长百分比出现下降的现象.例如,矩形双极板流道内GDL 平均侵入面积增长百分比由15.58 %降为12.54 %.而波浪形双极板流道内GDL 平均侵入面积增长百分比随着装配载荷的增加,由6.57 %进一步增加到7.54 %. 表7 GDL平均侵入面积增长百分比Tab.7 The growth percentage of GDL average intrusion area 本研究基于搭建的双极板压缩试验有限元模型进行了相关仿真分析,结果显示,双极板截面形状对双极板与GDL 之间的接触行为有显著影响,可能会造成PEMFC 电堆性能的差异性.结合分析讨论得出以下结论: 1)装配载荷和双极板截面形状对双极板下GDL表面整体平均接触应力幅值和GDL平均侵入面积有着非常显著的影响. 2)在不同装配载荷作用下,三种双极板肋下的GDL表面接触应力幅值均在0.5~2 MPa之间,均符合装配要求. 3)矩形双极板下GDL表面平均接触应力分布均匀性比梯形和波浪形双极板差. 4)在同等条件下,双极板肋宽度是决定GDL 表面整体平均接触应力幅值和GDL平均侵入面积的主要因素. 5)矩形双极板下的层间接触行为对装配载荷的变化更为敏感.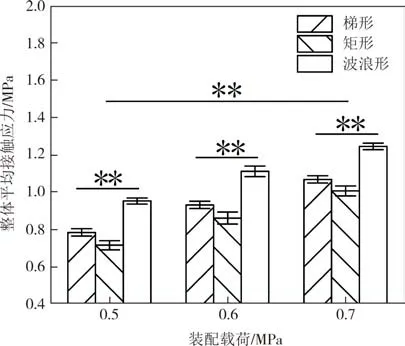

2.4 GDL侵入

3 结论
