考虑后续回击的500 kV 单回交流线路耐雷水平研究
2023-03-08杜志叶何靖萱柳双岳国华甘艳蔡泓威
杜志叶 ,何靖萱 †,柳双 ,2,岳国华 ,甘艳 ,蔡泓威
(1.武汉大学 电气与自动化学院,湖北 武汉 430072;2.国网湖北省电力有限公司超高压公司,湖北 武汉 430077;3.国家电网公司华中分部,湖北 武汉 430077)
雷电作为常见的自然灾害,给电力系统的安全稳定运行带来极大影响.据统计,2018 年4 月下旬印度安得拉邦13 h 内出现超4 万次闪电;2020 年2 月18 日澳大利亚新州1 d 内遭遇80 万次雷击[1];2021年5 月14 日湖北上空16 h 内出现超13 万次闪电.同时,传统的雷电参数统计给线路防雷评估带来了较大的误差.
一次云地闪放电过程包括的回击为4 次左右[2-5],分为首次回击及后续回击.目前国内外判断后续回击与首次回击是否来自同一放电过程的标准均从时空特点出发,根据二者击中大地的时间间隔及产生地面雷击点的距离进行判断.我国雷电定位系统的判断标准为后续回击与首次回击的时间间隔小于或等于1 s且二者的位置距离小于或等于10 km,同时相邻回击的时间间隔小于或等于500 ms[6].日本雷电定位系统、美国雷电定位系统的判断标准与我国相同[3,7].目前的研究表明,多回击地闪中,绝大部分为负地闪,占多回击总地闪回击总数的99.69%[8].
为了统计雷击杆塔过程中首次回击及后续回击的情况,国内外利用了高速摄像记录仪、宽带电场记录、雷电定位系统、卫星雷电探测、现场记录系统等多种监测手段,在研究过程中多集中于对记录到的云地闪放电过程中的回击数量、回击间隔以及首次回击及后续回击的比例、平均雷击点数、平均回击次数、峰值电流、强度等规律进行统计,并以此为基础分析后续回击对跳闸率的影响.
在雷电回击中有一定数量的后续回击会与首次回击击中同一个点[3-4],而且雷电流幅值相比首次回击更高[9-10].对于后续回击与首次回击击中一个点的情况,由于雷击先导通道前期已经形成,进而影响其雷击感应过电压与反击跳闸率.目前,针对后续回击影响跳闸率以及线路耐雷水平的研究较少,上海交通大学的江安烽等人[11]采用模型计算与理论仿真计算剖析了后续回击对10 kV 配电线路的反击跳闸率的影响,研究表明,对于后续回击与首次回击,反击跳闸率与中值电流有紧密联系,当后续回击的中值电流比首次回击大时,其反击跳闸率也更大.江安烽等人[12]对110/220 kV 双回输电线路反击跳闸率进行研究,发现不同回击类型的反击跳闸率不同,而若后续回击与首次回击的先导通道相同,由于其共用一个通道,其耐雷水平更低,反击跳闸率更高.而首次回击与创造新的通道的后续回击,由于其先导通道之前并未产生,所以反击跳闸率较小.
国外关于后续回击对反击跳闸率的影响也开展了较多的研究.巴西闪电研究中心的Silveira 等人[13]发现对69 kV线路而言,后续回击对反击跳闸率的影响比首次回击更大.Silveira 等人[14]研究了后续回击的影响与杆塔高度的联系,当杆塔高度超过30 m时,后续回击对杆塔雷电特性的影响更大(138 kV 输电线路).意大利航天电气与能源工程部的Gatta 等人[15]对150 kV 架空线路进行研究发现,后续回击对线路反击跳闸率的影响很大,在进行输电线路反击跳闸率计算时,需要考虑后续回击.
目前国内外对于后续回击的研究主要侧重于低压线路及高压输电线路,基本未涉及超高压输电线路,因此需要结合实际超高压输电线路的雷电统计规律,通过雷击仿真模型的改进来分析后续回击对雷击跳闸率的影响.由于多数多回击地闪为负极性,因此本文讨论的后续回击为负极性.
1 后续回击分布规律
1.1 回击次数
本文选取华中区域500 kV省间联络线重要输电通道的十条输电线路进行分析,数据来源于国家电网公司华中分部的调度信息系统,其中包括四条双回输电线路及两条单回输电线路,令十条线路编号为①~⑩,统计十条线路2016—2019年10 km 走廊范围内的负极性落雷如表1所示.

表1 十条线路10 km走廊范围内的落雷统计Tab.1 Statistics of lightning fall within 10 km corridor of 10 lines
由表1可知,2016—2019年在华中区域十条500 kV省间联络线内,后续回击次数平均约为首次回击次数的1.05 倍,且在此十条线路中有三条的后续回击次数明显超过首次回击次数.
1.2 雷电流幅值
我国各个区域的雷电流幅值概率分布曲线差异较大,表明各个区域雷电流的相关变化规律各不相同,此处采用IEEE 推荐雷电流幅值概率分布曲线表达式
其中,P表示雷电流幅值分布概率,I为雷电流幅值,a为中值电流,b反映了曲线的变化幅度.
依照以上公式,对线路⑤的数据进行拟合,得到的参数如表2 所示,得到相应的雷电流幅值概率分布拟合曲线如图1所示.纵坐标P(>I)表示雷电流幅值超过对应横坐标I的概率.

图1 各种放电类型的负极性回击的雷电流幅值概率拟合图Fig.1 Probability fitting diagram of lightning return strokes cur⁃rent amplitude of negative polarity lightning of various discharge types
由表2 的中值电流值可知,在不同放电类型的中值雷电流中,含后续回击的首次回击的雷电流幅值最大,表示在线路⑤10 km范围内含不同放电类型中,雷电流最为显著的是含后续回击的首次回击.

表2 不同放电类型雷电流幅值概率分布表达式的参数Tab.2 Parameters of different discharge type lightning am⁃plitude probability distribution expressions
从图1 可以直观看出,对于雷电流幅值概率分布曲线,总回击的拟合曲线位于后续回击与首次回击之间,表明考虑后续回击后,线路⑤10 km 范围内的雷电流会减小.
1.3 变异系数法
为了客观展现各个雷击跳闸指标的重要程度,需要计算出待分析的各个指标所占的比重来对各个指标进行客观赋权,以计算出的指标权重反映指标的重要性.若最终计算得出的包含后续回击的放电类型参数的权重较不包含后续回击的放电类型参数的权重更大,则可证明后续回击对雷击跳闸具有较大影响.
变异系数法[16]是一种易于操作、计算便捷的客观赋权方法.通过对收集到的客观数据进行分析、计算权重,从而判定各个指标的重要程度.这种方式可以避免人为主观判断,以权重表示重要程度,更具有说服力.
变异系数用来表征对象指标的变异程度水平,反映其离散程度,可消除不同评估指标量纲的影响.在评价指标体系中,指标的变异系数可以反映指标所覆盖的信息量:指标的变异系数越大,表明指标的各个取值差异性高,而差异性更高的指标会给最终结果提供更大的信息值,可说明其在评价对象指标中的重要程度越高,可以客观反映该指标对系统的影响.
在比较多个指标的变异程度时,首先要统一量纲,使用标准偏差与平均值的比值考虑指标.
变异系数法的相关步骤如下:
1)针对若干个参与对象,分别求解这些对象每个指标的平均数和标准差.
2)根据指标平均值和标准差计算全部指标的变异系数(此处假设有n个指标),可通过下式计算:
式中:Hi表示第i个指标的变异系数;σi表示第i个指标的标准差;xav-i表示第i个指标的平均值.
3)第i个指标权重Wi可通过下式求解得到:
基于所选华中区域十条500 kV线路雷击跳闸的相关负极性放电统计数据进行分析,令含后续回击的首次回击次数、雷电流幅值,不含后续回击的首次回击次数、雷电流幅值及后续回击的次数、雷电流幅值作为指标,将选取的六个负极性放电参数的指标进行分析,由于各个指标值的物理意义与单位不同,因此首先对输入参数进行量纲统一,通过变异系数法计算出六个参数的变异系数值和权重如表3所示.

表3 雷击跳闸的相关负极性放电参数的权重Tab.3 Weight of negative polarity discharge parameters re⁃lated to lightning strike trip
表3 中,x1表示含后续回击的首次回击次数,x2表示含后续回击的雷电流幅值,x3表示不含后续回击的首次回击次数,x4表示不含后续回击的雷电流幅值,x5表示后续回击的次数,x6表示后续回击的雷电流幅值.
由表3 可知,后续回击次数及含后续回击的首次回击次数两个参数对雷击跳闸的影响权重较大,表明后续回击对输电线路的影响较大,需要引起重视.
1.4 实际跳闸情况分析
为了验证通过变异系数法分析得到的结论,对本文所选华中区域十条500 kV 线路2016—2019 年的实际雷击跳闸情况进行统计分析,发现四年间十条线路中有5条线路总计出现了6次雷击跳闸故障,其中有3 次故障的故障塔在故障时刻的回击数在5次以上,选取线路③232#塔,其具体的跳闸情况如表4所示.
表4 列举了线路③雷电回击的综合回击点离故障杆塔的距离及雷电流幅值.由表中可知,在11 次雷击中,含1 次后续回击的首次回击的第一次后续回击点离故障点的距离为1.744 km.此回击在上述雷击中离故障点距离最近,且雷电流幅值达到了78.2 kA,可以判断232#塔跳闸是含1 次后续回击的首次回击的第一次后续回击引起的.

表4 线路③某一时刻记录到的回击情况Tab.4 Lightning return strokes recorded at sometime on line 3
同理,对故障时刻的回击数在5 次以上的故障塔进行分析,数据表明,线路⑥21#塔故障由含2 次后续回击的首次回击引起,线路⑦445#塔故障由含3次后续回击的首次回击引起.
综上可知,在充分考虑杆塔发生雷击跳闸故障时的雷电流幅值及回击点离故障点的距离两个因素后,分析得出含后续回击的首次回击与后续回击这两种放电类型是引起杆塔跳闸的原因.
2 考虑后续回击的绝缘子串闪络判据模型
2.1 常规的绝缘子串闪络判据模型
绝缘子串闪络的三种判断方法的主要特点如下:规程法是以根据运行经验得到的绝缘子串50% 冲击击穿电压U50%为基础,通过比较绝缘子串两端实时的过电压值与U50%的大小来判断其是否闪络;相交法是以实验得到的绝缘子串的伏秒特性曲线为基础,通过观察绝缘子串两端的实时电压波形与伏秒特性曲线是否相交来判断其是否闪络,U50%以及伏秒特性曲线均在雷电冲击电压条件下通过实验获得.
先导法对应的理论中的放电过程与实际情况下的雷击较为类似,对于绝缘子串而言,先导法可以克服规程法及相交法的缺点,采用与绝缘子串等长空气间隙的闪络过程[17]替代绝缘子串的实际闪络过程,可以判断任意波形造成的闪络.由于自然雷电主要为非标准雷电冲击波,且先导法通过分析雷电放电机理形成闪络判据,因此本文选取先导法[18]作为常规的绝缘子串闪络判据.
对于长空气间隙放电,间隙击穿时间可以近似为流注放电时间t1及先导发展时间t2[19]之和,若流注放电时间大于0,则表明会发生流注放电过程.
其中,Emax为绝缘子串闪络前的最大平均场强,E50为50%放电电压对应的空气间隙的平均场强.
其中,v2为先导发展的速度,L1为先导发展部分的间隙长度.
其中,d为长空气间隙的长度,u(t)为绝缘子串两端的瞬时电压差,L2为长空气间隙的剩余长度,E0为先导发展的初始场强,是由绝缘子串种类及其两端施加电压的极性确定的常数.
在先导发展时间t2内,若先导发展速度大于0,则表明先导完全发展导致长空气间隙击穿,则绝缘子串的闪络判据为t1>0及v2>0.
2.2 考虑后续回击的绝缘子串闪络判据模型
由式(4)可知,流注放电时间与绝缘子串闪络前的最大平均场强Emax及50%放电电压对应的空气间隙的平均场强E50有关,其中Emax与绝缘子串两端的瞬时电压差u(t)有关,E50为常数,则流注放电时间与回击放电类型无关.
由式(5)可知,先导发展部分的间隙长度L1与先导发展速度v2及先导发展时间t2有关.由式(6)可知,v2>0 与绝缘子串两端的瞬时电压差u(t)、间隙的剩余长度L2及先导发展的初始场强E0有关,E0为常数,L2为长空气间隙长度d与L1之差.
后续回击沿首次回击的先导发展通道向下延伸时,由人工引雷的大量实验数据可知,后续回击的先导发展速度与首次回击相比较快[20],令考虑后续回击时的先导发展速度为v3,相应的先导发展部分的间隙长度为L3,则
其中,a为比例系数,表示后续回击发展比首次回击快的程度,与沿首次回击的先导发展通道的后续回击比例a1及后续回击与首次回击之比a2有关.
根据已有研究可知[21-22],与沿首次回击的先导发展通道的后续回击比例约为45.5%,即根据第1 节后续回击分布规律的统计分析可知,对负极性放电,由表1 可推出,后续回击是首次回击的1.33 倍,则a取0.6.式(6)变为
则考虑后续回击的绝缘子串闪络判据为t1>0 及v3>0.考虑后续回击的绝缘子串闪络判据流程图如 图2所示.

图2 考虑后续回击的绝缘子串闪络判据流程图Fig.2 Flow chart of insulator string flashover criterion consider⁃ing subsequent return stroke
3 后续回击对单回输电线路耐雷水平的影响
3.1 反击耐雷水平
当输电杆塔遭受雷击后,输电线路绝缘子串承受的电压差幅值可用式(11)表示
其中,Ua为绝缘子串的横担侧电压,U1、Ui(c)、U2分别为导线上的耦合电压、感应过电压及工频电压.
负极性雷击中杆塔塔顶时,塔顶为负电位,U1与Ui(c)分别为负极性、正极性.首次回击跳闸且重合闸成功之后,绝缘子串两端的电压差恢复到跳闸之前的电压水平,此时再考虑后续回击的情况与首次回击未跳闸的情况相同,因此本文考虑后续回击对线路耐雷水平的影响时,仅考虑首次回击未跳闸的情况.
根据如图2 所示的考虑后续回击的绝缘子串闪络判据及考虑后续回击的雷电流模型,建立基于图3原理流程的考虑后续回击的仿真模型,为贴近华中区域雷击频发的老旧线路运行工况,模型不含避雷器等防雷装置,杆塔塔型为酒杯型.
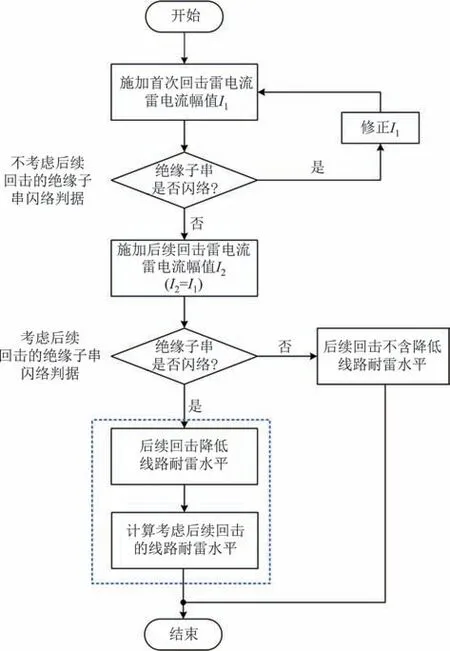
图3 考虑后续回击的线路雷击仿真模型原理逻辑图Fig.3 Schematic diagram of line lightning simulation model considering subsequent lightning return stroke
初步设置t=0 时,B 相的工频电压值为0.500 kV导线上的工作电压的频率为50 Hz.通道波阻抗设为300 Ω,接地电阻设为10 Ω,不考虑后续回击时线路的反击耐雷水平为191.434 kA,B 相绝缘子串两端的过电压为3.85 MV.
取首次回击雷电流幅值I1为191.434 kA,即首次回击不会跳闸,设仿真时间为0.2 s,取其中一个运行周期(0.1 s ≤t≤ 0.12 s)进行分析,在t时刻施加雷电流,其幅值I2=191.434 kA,若绝缘子串闪络,可证明考虑后续回击后,线路的反击耐雷水平降低,并计算线路的反击耐雷水平.
以t=0.105 s为例,如图4所示.
从图4 中可以看出,考虑首次回击未跳闸,稳定之后绝缘子串两端的电压为线路的工频电压,考虑后续回击跳闸后,跳闸相绝缘子串两端的电压变为0,绝缘子串闪络,线路的反击耐雷水平降低.

图4 t=0.105 s考虑后续回击绝缘子串两端电压变化图Fig.4 Diagram of voltage changes at both ends of subsequent lightning return stroke when t=0.105 s
一个运行周期(0.1 s ≤t≤ 0.12 s)中,考虑后续回击后线路的反击耐雷水平如表5所示.

表5 考虑后续回击后线路的反击耐雷水平Tab.5 The lightning back-flashover resistance level of the line considering the subsequent return
对于雷击产生的过电压幅值,在t=0.1 s、0.11 s及0.12 s三种情况下考虑后续回击,即在B 相的工频电压过零点考虑后续回击,跳闸时B 相绝缘子串两端的过电压幅值小于3.85 MV.
在t=0.105 s 时考虑后续回击,即为B 相的正半周工频电压峰值点,当考虑后续回击跳闸时,B 相绝缘子串两端的过电压幅值大于3.85 MV;在t=0.115 s时考虑后续回击,即为B 相的负半周工频电压峰值点,当考虑后续回击跳闸时,B 相绝缘子串两端的过电压幅值小于3.85 MV.
因此,后续回击雷电流为原反击耐雷水平时,绝缘子串承担的过电压与原来承担过电压之间的关系与导线工频电压周期有关.
对于线路反击耐雷水平,由表5 可知,考虑后续回击后,计算出的线路的反击耐雷水平降低,同时,不同时刻的降低程度不同,且与工频电压周期有关,平均降低原反击耐雷水平的36.4%.
3.2 绕击耐雷水平
在考虑后续回击的反击仿真模型的基础上,改变雷电流模型的通道波阻抗为400 Ω,改变雷击点的位置,建立考虑后续回击的绕击仿真模型.
调整交流电源的相位使t=0 时刻A 相的工频电压值为500 kV.t=0 s时,U为500 kV,此时发生首次回击,接地电阻设为10 Ω,不考虑后续回击时线路的绕击耐雷水平为25.259 kA,A 相绝缘子串两端的过电压为3.90 MV.
取首次回击雷电流幅值I1为25.259 kA,即首次回击不会跳闸,由于线路发生首次回击后,所引起的绝缘子串两端电压差恢复成正弦状态所需时间较短,因此为方便仿真计算,将考虑后续回击的时刻t=0.5 s 类同于t=0.1 s,施加后续回击雷电流,其幅值为I2=25.259 kA,若绝缘子串闪络,可证明考虑后续回击后,线路的反击耐雷水平降低,并计算线路的耐雷水平.
设仿真时间为0.2 s,取其中的一个周期(0.1 s ≤t≤ 0.12 s)进行分析得出考虑后续回击后线路的绕击耐雷水平如表6所示.
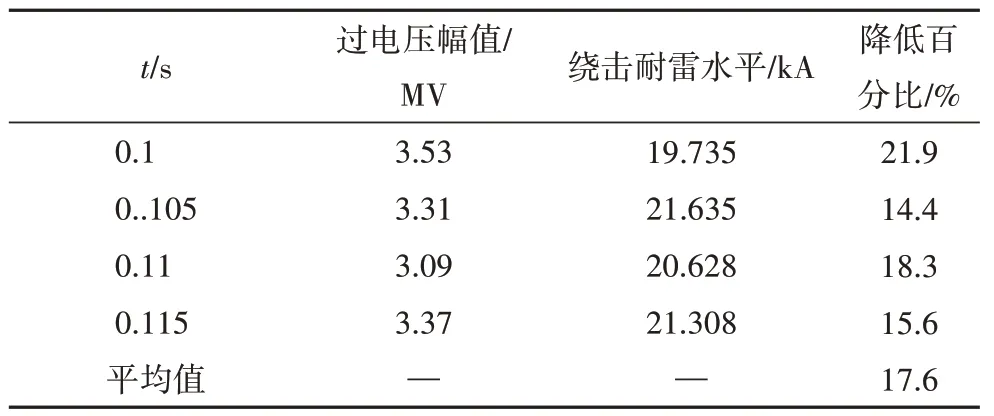
表6 考虑后续回击后线路的绕击耐雷水平Tab 6 The lightning shielding resistance level of the line considering the subsequent return
由表6 可知,考虑后续回击后线路的绕击耐雷水平会降低,同时,不同时刻的降低程度不同,且与工频电压周期有关,平均降低原绕击耐雷水平的17.6%.
综合考虑后续回击对输电线路耐雷水平的影响发现,后续回击会使500 kV 输电线路的耐雷水平降低,且后续回击对绕击耐雷水平的影响程度与反击耐雷水平相比较小.
4 原因分析
本文考虑后续回击对输电线路跳闸的影响时,重点在于与首次回击保持相同通道的后续回击,在分析后续回击对反击及绕击耐雷水平的影响时,导致跳闸的后续回击出现的概率假设一致均为k,则根据图1 可得,在已知首次回击的雷电流幅值概率分布曲线时,雷电流幅值概率k提高,对应的雷电流降低值如图5所示.

图5 雷电流幅值概率分布拟合图Fig.5 Lightning current amplitude probability distribution fit⁃ting diagram
由图5 可知,当雷电流幅值概率k提高时,25 kA对应的绕击雷电流降低值ΔI1小于190 kA 对应的反击雷电流降低值ΔI2,则后续回击对反击耐雷水平的影响程度更为严重,与仿真计算结果一致.
5 结论
本文通过对华中区域十条500 kV省间联络线重要输电通道线路走廊10 km 范围内近年来的落雷数据进行分析,得出如下结论:
1)得到了后续回击的分布规律,后续回击次数为首次回击次数的1.33 倍,后续回击次数30%以上比首次回击次数多,且考虑后续回击后线路走廊范围内的雷电流会减小.
2)利用变异系数法完成了后续回击对输电线路影响的分析,并利用实际线路运行跳闸数据进行验证,结果表明后续回击次数的两个参数对雷击跳闸的影响权重较大,需要引起重视.
3)建立了考虑后续回击的绝缘子串闪络判据模型,仿真结果表明后续回击会使500 kV 输电线路的耐雷水平降低,且降低程度与工频电压周期有关,后续回击对反击耐雷水平的影响程度与绕击耐雷水平相比更为显著.
