零耦合度部分运动解耦2T1R并联机构拓扑与性能研究

2023-03-07沈惠平朱晨阳

农业机械学报 2023年2期

沈惠平朱晨阳李菊李涛

(常州大学现代机构学研究中心, 常州 213016)

0 引言

三自由度两平移一转动并联机器人机构因驱动元件少、制造方便，在工业生产中具有较高实用价值[1]，可用于空间物品的拾取操作、设备的姿态调整等[2]。国内外机构学研究人员对此类机构已进行广泛深入的研究。HUNT[3]于1983年设计了一种含2T1R及其奇生运动的3-DOF空间机构；KONG等[4]研究了含有球面支链或平行四边形子支链的2T1R空间机构；LIU等[5]提出一组运动学求解和构造均较为简单的2T1R型并联机构；刘艳敏[6]研究机构的综合方法，并优选了部分2T1R新机型。

机构位置求解是并联机构研究中最基础、最重要的问题之一[7]，目前，大多数学者应用杆副法[8]、回路法[9]，来建立机构输入-输出位置方程，但为得到一般的非线性一元高次方程，其数学推导、消元过程十分复杂。杨廷力[10]提出了机构运动学分析的序单开链法；沈惠平[11]提出了并联机构的拓扑特征运动学建模原理和方法，具有建模方便、计算量大大减少等优势。

动力学分析是保证机构动力学性能的前提。目前，机构的动力学分析方法主要有：虚功原理法[12-13]、拉格朗日法[14-15]、牛顿-欧拉法[16-17]、凯恩法[18-19]、动力学普遍方程[20]、Hamilton正则方程[21]等。拉格朗日法表现形式简单，但其计算量较大；凯恩法有较为简洁的计算方法，但对于力和力矩的分析相对匮乏[22]；牛顿-欧拉法对于构件较多的机构受力分析较复杂，但在构建动力学模型时易求出运动副的约束反力[23]；虚功原理同拉格朗日法一样，表现形式统一、计算量较大，且无法得到构件的约束反力。

基于虚功原理的序单开链法，以子运动链为基本单元，不仅能求出各驱动副的驱动力，还能求出子运动链(SKC)连接处的支反力，这对机械结构强度设计至关重要[24]。

本文根据基于方位特征(POC)方程并联机构拓扑设计理论[25]，提出一种零耦合度、含一条混合支链的空间2T1R并联机构；对该机构进行拓扑特性和运动学分析；基于虚功原理的序单开链法建立该机构的逆向动力学模型，求解机构驱动力及部分运动副支反力；最后，对该机构应用于物流领域输送带之间物料的自动转运、卸料装置的应用场景，进行概念设计。

1 机构设计和分析

1.1 机构设计

1.1.1POC方程

串联、并联机构的POC集计算公式[25]为

(1)

(2)

式中MS——末端构件POC集

Mji——第i个运动副POC集

Mbi——第i条支链末端POC集

MPa——机构动平台POC集

1.1.2机构设计思路

大量研究表明，含有混合支链的并联机构一般具有耦合度低、输入-输出(部分)运动解耦、易得符号式位置正解等优点[11,24]，且其运动学、刚度以及动力学综合性能也较好；且含1-DOF、2-DOF混合支链数目越多，机构输入-输出(部分)运动解耦性能越好，其运动学/动力学求解越容易，因为(1～2)-DOF混合支链本身的位姿易求得；另外，两支链并联机构具有结构简单、动平台转动能力强、干涉少等优点[25]。

根据上述思路，一方面，为设计具有“零耦合度且运动解耦”特性的并联机构，可以通过构造约束度为零、含部分驱动副且可独立求出其位置回路的混合支链，以实现设计目标；另一方面，本文设计的2T1R并联机构采用两支链的结构来实现，这意味着两条支链的末端运动输出最少都须包含2个平移(2T)和1个转动(1R)元素。

1.1.3支链设计

设计一个两滑块两平移空间并联机构，如图1a所示，它由分支1(P11‖R12‖R13‖R14)、分支2(P21⊥R22‖R23)并联而成，其中，两移动副P11和P21为重合共线，该机构简记为：2P-5R，为阐述方便，在静平台0上，建立坐标系OXYZ，Y轴平行于P11(或P21)，Z轴平行于静平台0的法线。

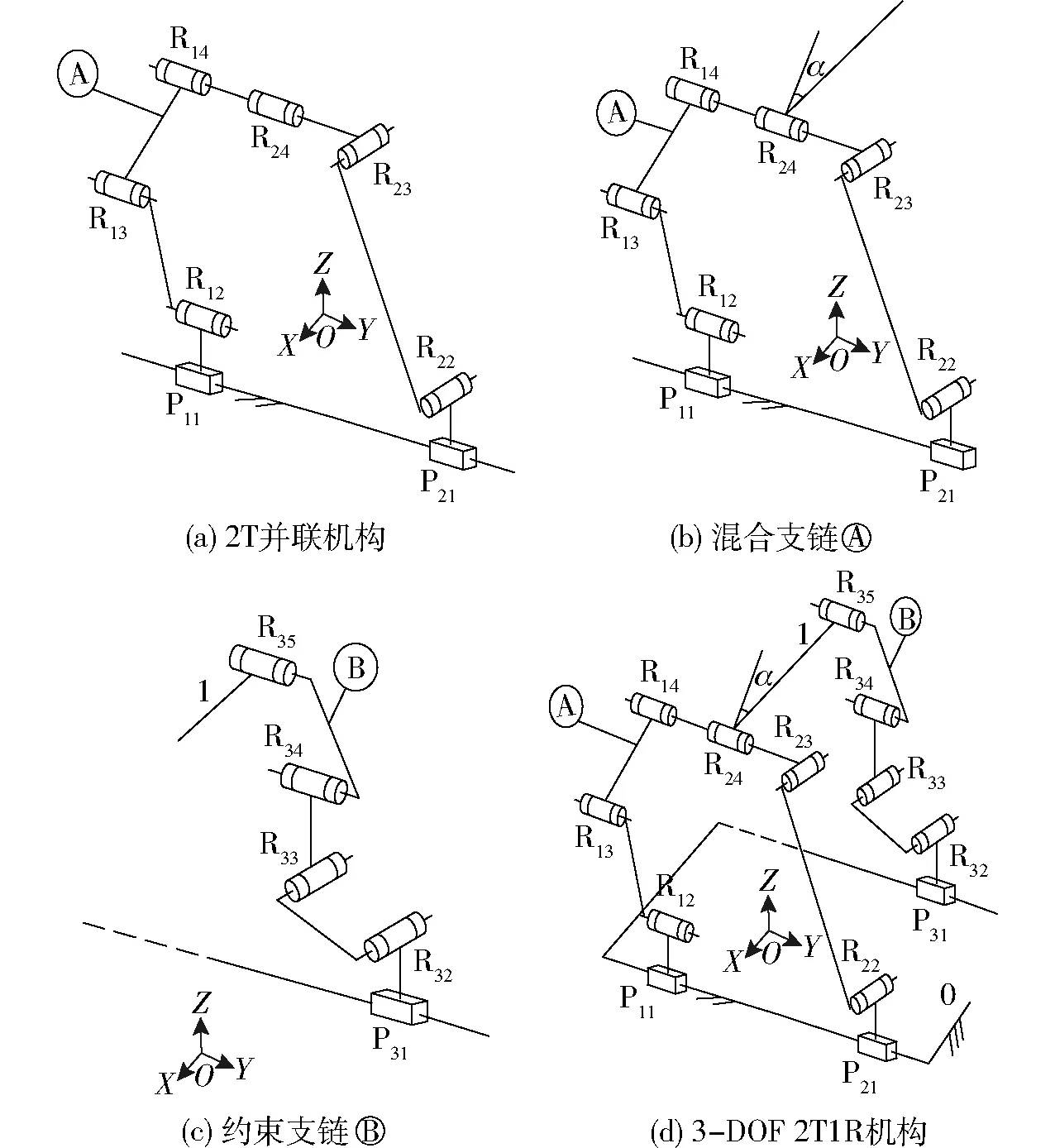
图1 3-DOF 2T1R 机构的设计过程

由式(1)可知，分支1、2末端构件的POC集均为

由式(2)可知，输出构件2的POC集为

因此，输出构件2将产生垂直于R22轴线的平面(YOZ)内的两维移动(2T)。

在输出构件2的轴线上，直接串联一个转动副R24，如图1b所示，即转动副R24与R14共轴线(均平行于Y轴)，则构成另一条混合支链，它将连接动平台1左端，由式(1)可知

MA=M2∪MR24=

(3)

(4)

使动平台1上转动副R35‖R24，且P31‖P11，从而设计出由混合支链、约束支链连接的2T1R并联机构[26]，如图1d所示；由式(2)知，其动平台1的POC集为

因此，设计的并联机构具有沿YOZ平面内的两维移动和绕Y轴的一维转动。

1.2 拓扑分析

1.2.1机构自由度

(1)机构全周自由度计算公式[25]为

(5)

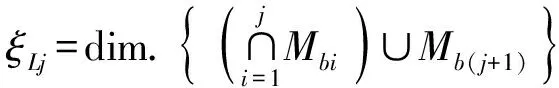
(6)

v=m-n+1

式中F——机构自由度

fi——第i个运动副自由度

m——运动副数

v——独立回路数

n——构件数

ξLj——第j个独立回路独立位移方程数

Mb(j+1)——前j+1条支链末端构件的POC集

第1回路为2P-5R空间机构，由式(6)得其独立位移方程数为

ξL1=dim.{Mb1∪Mb2}=

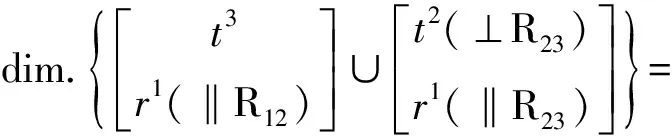
由式(5)得其自由度为

第2个回路由上述子并联机构、转动副R24及支链构成，由式(6)得其独立位移方程数为

ξL2=dim.{MA∪MB}=

因此，由式(5)得机构自由度

因此，当选取静平台0上移动副P11、P21、P31作为驱动副，该机构动平台1可实现YOZ平面内的两维平移以及绕Y轴的一维转动的输出运动。

1.2.2机构耦合度

由基于序单开链(SOC)的机构组成原理[25]知，机构均可划分为若干(SKC)，而SKC又可分解为若干单开链(SOC)，第j个SOCj的约束度为

(7)

式中mj——第j个SOCj运动副数

Ij——第j个SOCj驱动副数

则SKC耦合度κ为

(8)

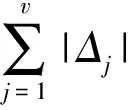
1.2.1节已计算出ξL1=5、ξL2=5，因此，由式(7)可分别求出第1、2回路的单开链约束度为

易知，上述2个回路可分别独自构成子运动链，即SKC1及SKC2，由式(8)可得其耦合度为

因此，SKC1、SKC2可独立求解，从而可使机构求得符号式位置正解[26]。

至此，该机构主要拓扑性能(DOF、κ)已求出，并到达所期望的设计目标，其具有优点：①由低副组成，加工制造容易。②机构为零耦合度，因此具有符号式位置正解。③含两个子运动链且分别含有驱动副，因此具有部分运动解耦特性，从而有利于该机构运动学和动力学的建模与性能求解。

2 并联机构运动学分析

机构运动学模型如图2所示，静平台0上两个导轨之间距离为l8。静坐标系OXYZ的坐标原点O在导轨所在两条直线的中线上，Y轴方向平行于A1A2连线，Z轴平行于导轨所在平面的法线方向，并指向动平台1；动坐标系O′X′Y′Z′的原点位于动平台1的R24几何中心，X′、Y′轴分别重合、垂直于D2D3连线，而X轴、Z′轴方向均由右手定则确定。

图2 机构运动学模型

2.1 位置正解分析

已知点Ai(i=1,2,3)驱动副输入量y1、y2、y3，求解动平台1上点O′的位置(x,y,z)及动平台姿态角α。机构位置正解可由SKC1和SKC2分别求得。

(1)SKC1位置求解

易有A1=(l8/2，y1，0)，A2=(l8/2，y2，0)，B1=(l8/2，y1，l1)，B2=(l8/2，y2，l1)，D1=(l8/2，y1，z)，C2=(l8/2，y1+2l3，z)，D2=O′=(l8/2，y1+l3,z)。

由杆长约束lB2C2=l4得位置约束方程，并求得

(9)

(2)SKC2位置求解

易有：A3=(-l8/2,y3,0)，B3=(-l8/2,y3,l1)。因两导轨道间距离为l8，故D2-D3-C4组成的回路在XOZ面上的投影关系如图3所示。

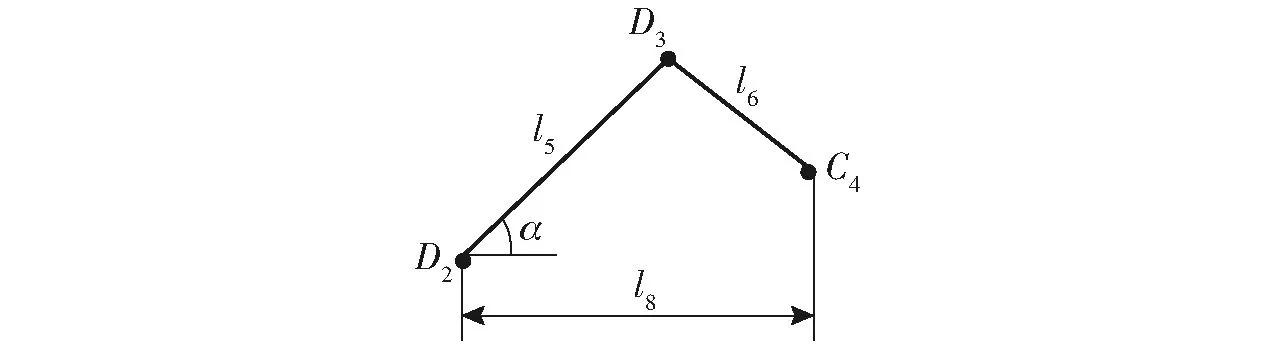
图3 D2-D3-C4在XOZ面上的投影关系

显然，有D3=(l8/2-l5cosα,y1+l3,z+l5sinα)，C4=(-l8/2,y1+l3,ZC4)，而C3=(-l8/2,y1+l3,ZC4-l7)。

(10)

由杆长约束lC3B3=l6得约束方程并解得

(11)

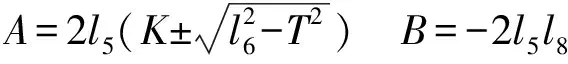
因此，由式(8)、(11)可得动平台(x,y,z)及姿态角α。

2.2 位置逆解分析

已知动平台1位置(x，y，z)及动平台姿态角α，求驱动副输入量y1、y2、y3。

由几何约束条件lB3C3=l6得到

根据式(9)、(11)可得

(12)

由式(12)可知，驱动副输入量y3、y2各有2组解，因此，此机构可有4组逆解。

2.3 正逆解实例验算

设机构结构参数为l1=100 mm，l2=220 mm，l3=150 mm，l4=440 mm，l5=600 mm，l6=320 mm，l7=80 mm，l8=600 mm。

设3个驱动副输入量y1、y2、y3分别为-340、50、60 mm。通过Matlab计算式(9)、(11)可得到6组位置正解，如表1所示。

将表1中序号1的数据代入式(12)，可以求得4组位置逆解。如表2所示，其中序号1的逆解数值与求解正解时给定的3个驱动输入量一致。

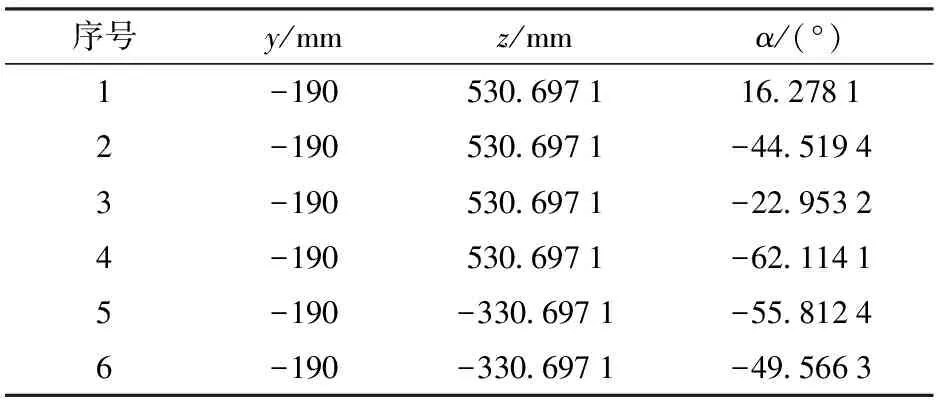
表1 位置正解

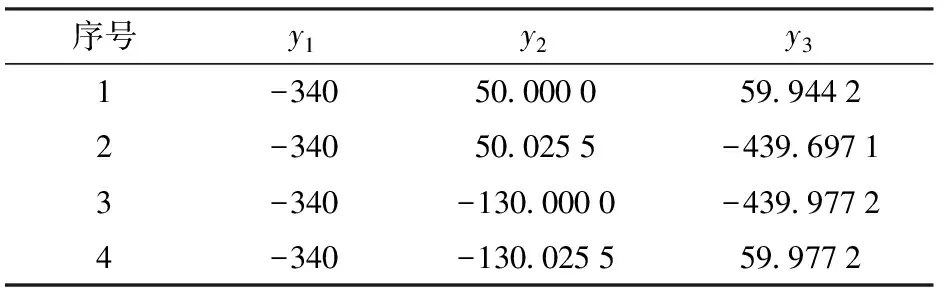
表2 位置逆解

3 工作空间

并联机构可达空间是指在考虑运动副转角范围、杆长不干涉情况下，末端执行器的工作区域，是衡量并联机器人性能的一个重要指标。

传统的工作空间计算是基于位置反解求得的点，由这些点组成的三维图即为该机构工作空间。

而本文机构具有符号式位置正解，因此，直接采用位置正解来计算工作空间，计算量少且工作空间边界计算准确。

为此，确定3个驱动副位置搜索范围为：-430 mm≤y1≤-320 mm，300 mm≤y2≤410 mm,-320 mm≤y3≤320 mm，搜索范围只需大于杆件活动范围即可。通过Matlab软件编程，得到该并联机构动平台质心点的三维工作空间如图4a所示，其XOZ、YOZ截面如图4b、4c所示。

图4 机构动平台质心点工作空间

4 奇异性与速度分析

4.1 机构奇异性分析方法

(13)

其中

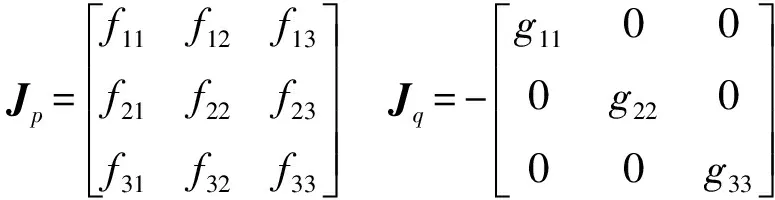
f11=-2(yD1-y)f12=0f13=0

f21=-2(yB2-yC2)f22=2(zB2-zC2)f23=0

f31=-2(yB3-yC3)f32=-2(zB3-zC3)

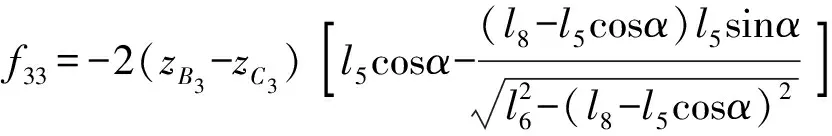
g11=-2(yD1-y)g22=-2(yC2-yB2)

g33=yC3-yB3

当机构不存在奇异位置时，Jp可逆，得

(14)

式(14)即为动平台基点输出速度。

为方便后续计算，现将动平台速度矩阵分解为移动矩阵和转动矩阵，即

由此，移动、转动矩阵与原矩阵的关系可表示为

其中

这样，动平台基点的移动、转动速度矩阵，与3个输入角之间的关系可分别表示为

将式(13)对时间t求导，得到动平台点O′加速度与输入加速度之间的映射关系为

(15)

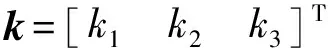
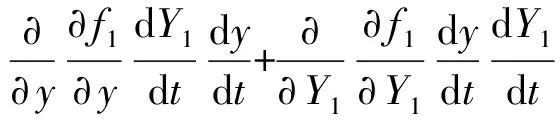
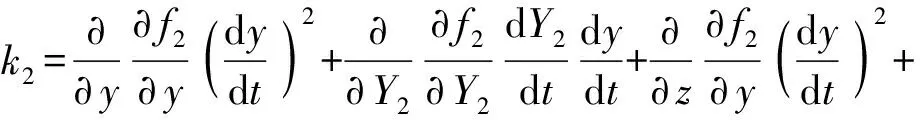
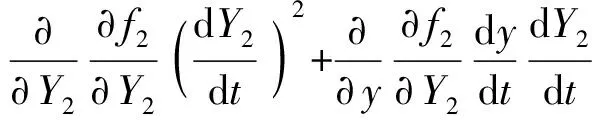
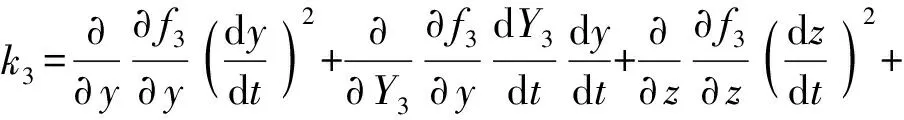
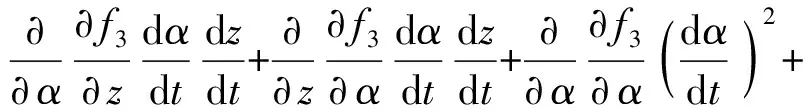
4.2 奇异性分析

4.2.1输入奇异

当机构发生输入奇异时，机构的执行构件将失去某个方向的运动能力，此时，至少有1个运动链到达工作空间的边界。

当det(Jq)=0，机构将发生输入奇异，将方程的解集设为A，则A为

A={A1∪A2∪A3}

其中，Ai(i=1，2，3)为机构产生输入奇异时的3种情况：当A1={yD1=y}不满足构型要求，舍去。当A2={yC2=yB2},即点C2与点B2的y轴坐标相等，满足A2的三维构型如图5所示。当A3={yC3=yB3}，即点C3与点B3的y轴坐标相等时，机构发生输入奇异，满足A3的三维构型如图6所示。

图5 A2的输入奇异位形

图6 A3的输入奇异位形

4.2.2输出奇异

当det(JP)=0时，机构发生输出奇异。由于Jq为下三角矩阵，故方程的解F={f11∪f22∪f33}，其中，f11、f22不满足构型要求，舍去。

当f33=0，机构发生输出奇异，有两种情况：

第1种情况：当机构满足ZC3=ZB3时，如图6所示，即运动副C3和B3在水平方向平行时，机构无法继续运动，此时机构发生输出奇异，如图7所示。

图7 ZC3=ZB3的输出奇异位形

第2种情况：当动平台转动角满足

此时，机构将发生输出奇异。

4.2.3综合奇异

综合奇异即输入奇异与输出奇异同时发生。当det(JP)=det(Jq)时，机构发生综合奇异。此机构不存在综合奇异位置。

4.3 杆件速度与加速度

杆件AiBi速度与加速度关系为

VBi=VAi+ωi×(l1ci)

(16)

式中VAi——驱动副(Pi)线速度

ωi——驱动杆AiBi角速度

ci——杆AiBi单位矢量

因驱动副在机架上且仅为移动驱动，所以ωi=0。对式(16)求导，得点Bi加速度为

aBi=aAi

式中aAi——驱动副Pi1线加速度

于是，杆件AiBi质心速度、加速度分别为

(17)

杆件C1B1速度为

VC1=VB1+ω5×(l2C5)

(18)

两边叉乘C5可得

(19)

式中C5——杆件B1C1单位矢量

将式(18)两边对时间t求导，得

aC1=aB1+l2ε5×C5+l2ω5×(ω5×C5)

(20)

对式(20)两边叉乘C5，得杆件B1C1角加速度为

(21)

由式(18)、(20)得杆件B1C1质心速度、加速度为

(22)

杆件C1D1速度与加速度关系为

VD1=VC1+ω6×(l2C6)

(23)

两边叉乘C6，得

(24)

式中C6——杆件C1D1单位矢量

将式(23)两边对时间t求导，得

aD1=aC1+l2ε6×C6+l2ω6×(ω6×C6)

(25)

对式(25)两边叉乘C6，得杆件C1D1角加速度为

(26)

由式(23)、(25)得杆件C1D1质心速度与加速度为

(27)

杆件D1D2速度与加速度关系为

VD1=VC1aD1=aC1

则杆件D1D2质心速度、加速度为

(28)

杆件C3C4速度与加速度关系为

VC4=VC3

aC4=aC3

则杆件C3C4质心速度、加速度为

(29)

其余构件速度与加速度求法类似，故不再赘述，直接给出结果。

杆件B2C2、B3C3质心速度、加速度分别为

(30)

(31)

(32)

(33)

杆件C2D2、D3C4质心速度、加速度分别为

(34)

(35)

(36)

4.4 算例与仿真

给定3个驱动副的运动规律分别为

由式(14)、(15)，通过Matlab计算得到动平台基点的理论速度和加速度，如图8、9所示。

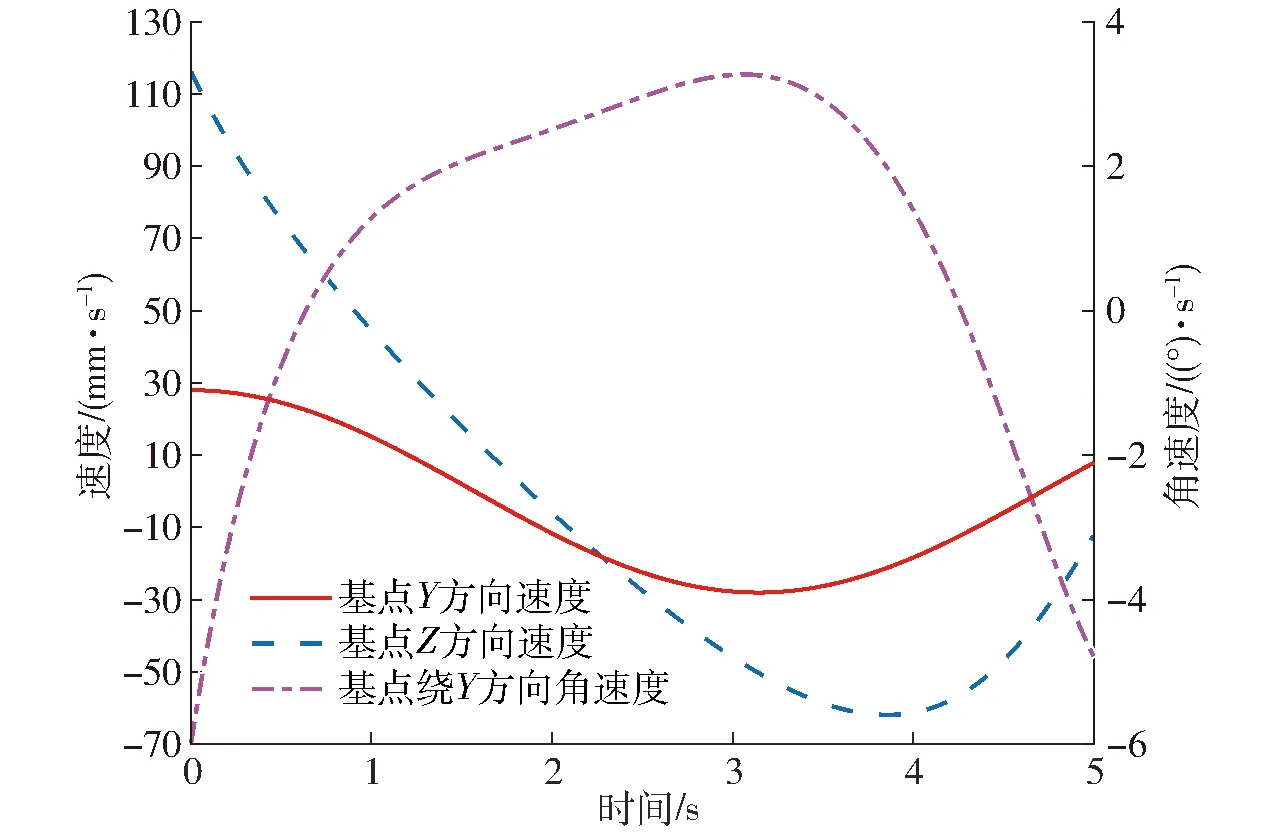
图8 动平台理论速度曲线

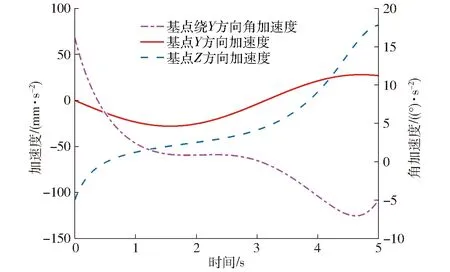
图9 动平台理论加速度曲线

通过ADAMS仿真，得到动平台基点的速度与加速度曲线，分别如图10、11所示。

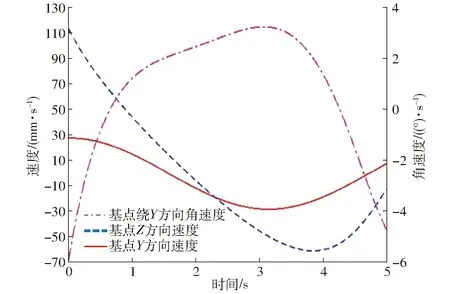
图10 动平台仿真速度曲线

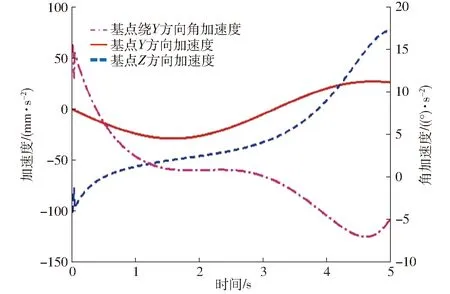
图11 动平台仿真加速度曲线

对比图8和图10，以及图9和图11，可知该机构速度、加速度理论值与仿真值一致，存在微小误差，验证了运动学模型的正确性。

5 动力学分析

5.1 基于虚功原理的序单开链法基本原理

5.2 部分构件雅可比矩阵

由于动平台在Y、Z方向上移动并绕Y方向转动，动平台上另一点D3的速度与O′速度不同，且无法直接表达出动平台质心点处的雅可比矩阵，故采用与第4节相同的方法求解以点D3为基点时动平台的雅可比矩阵。

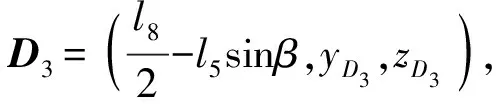
(37)

式中β——杆件D3D2绕Y轴方向的夹角

由式(37)可得，动平台质心处、D3C4质心处的雅可比矩阵分别为

式中，JC4可由点C4速度直接表达出。

5.3 受力分析

作用于构件质心上的力有重力和惯性力，而力矩仅为惯性力矩。

对于动平台，作用在质心的力和力矩分别为

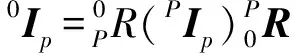
式中f′、τ——作用在动平台的外力和外力矩

R——在静坐标系{o}中动平台质心处的惯量矩阵，为旋转矩阵

Ip——动平台质心处惯量矩阵

对于各支链，假设重力是唯一的外力，则作用在各构件上的力和力矩分别为

Fi=mig-miamidi

Mi=-oIiεi-ωi×(oIiωi) (i=1，2，…，12)

式中oIi——在静坐标系{o}中各杆件质心处的惯量矩阵

5.4 动力学方程

对于SKC2，解除运动副D2处的约束，于是支反力FD2转换为未知外力，由虚功原理可得

(38)

在静坐标系{o}中，以杆D2D3为研究对象，并将力系向D3处简化，可得

(39)

对于SKC1，将支反力FD2视为未知外力，由虚功原理可得

(40)

由式(38)～(40)可得机构的驱动力F11、F21、F31，以及运动副D2处的支反力FD2。

5.5 数值仿真算例

机构各构件尺寸参数如表3所示。

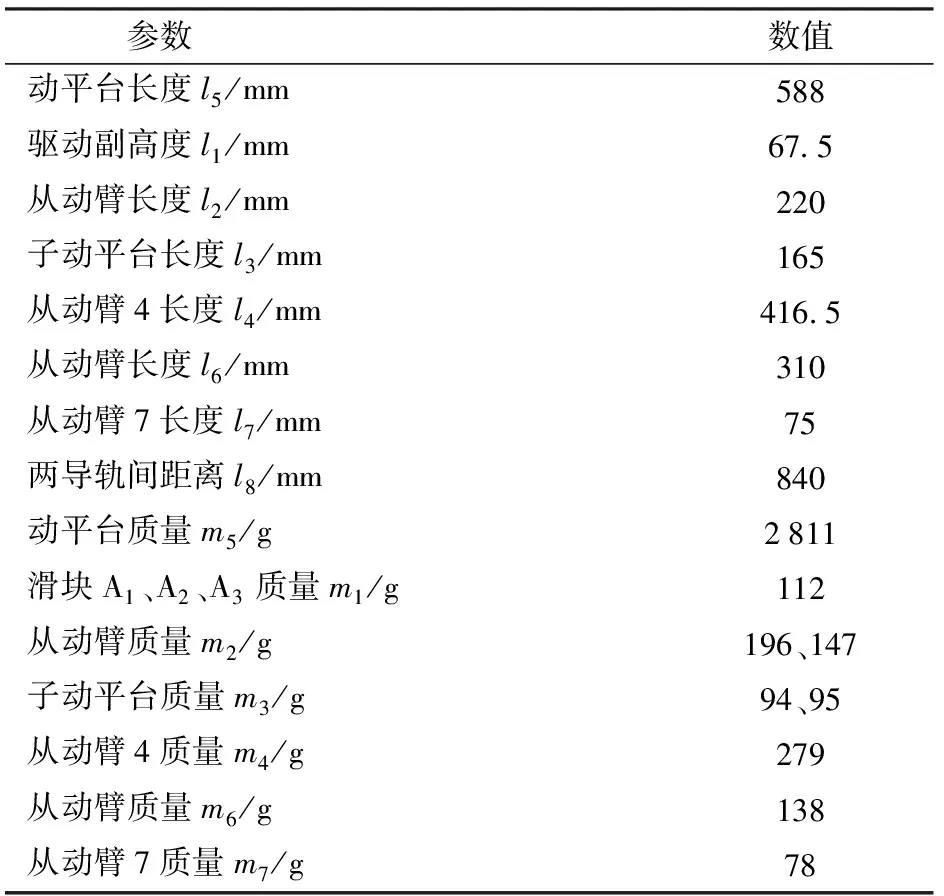
表3 2T1R并联机构尺寸参数

仅考虑动平台受沿Z轴方向的载荷。各构件均为形状规则、质量均匀的刚体，且驱动副采用与4.4节相同的运动规律，通过Matlab编程计算式(38)、(40)，得驱动力F关于时间t的曲线，如图12a所示；将虚拟样机导入ADAMS中，并设定各构件的材料属性、运动副的约束类型，施加竖直向下的重力，选取仿真步长0.01 s，仿真时间5 s，动力学仿真曲线如图12b所示。

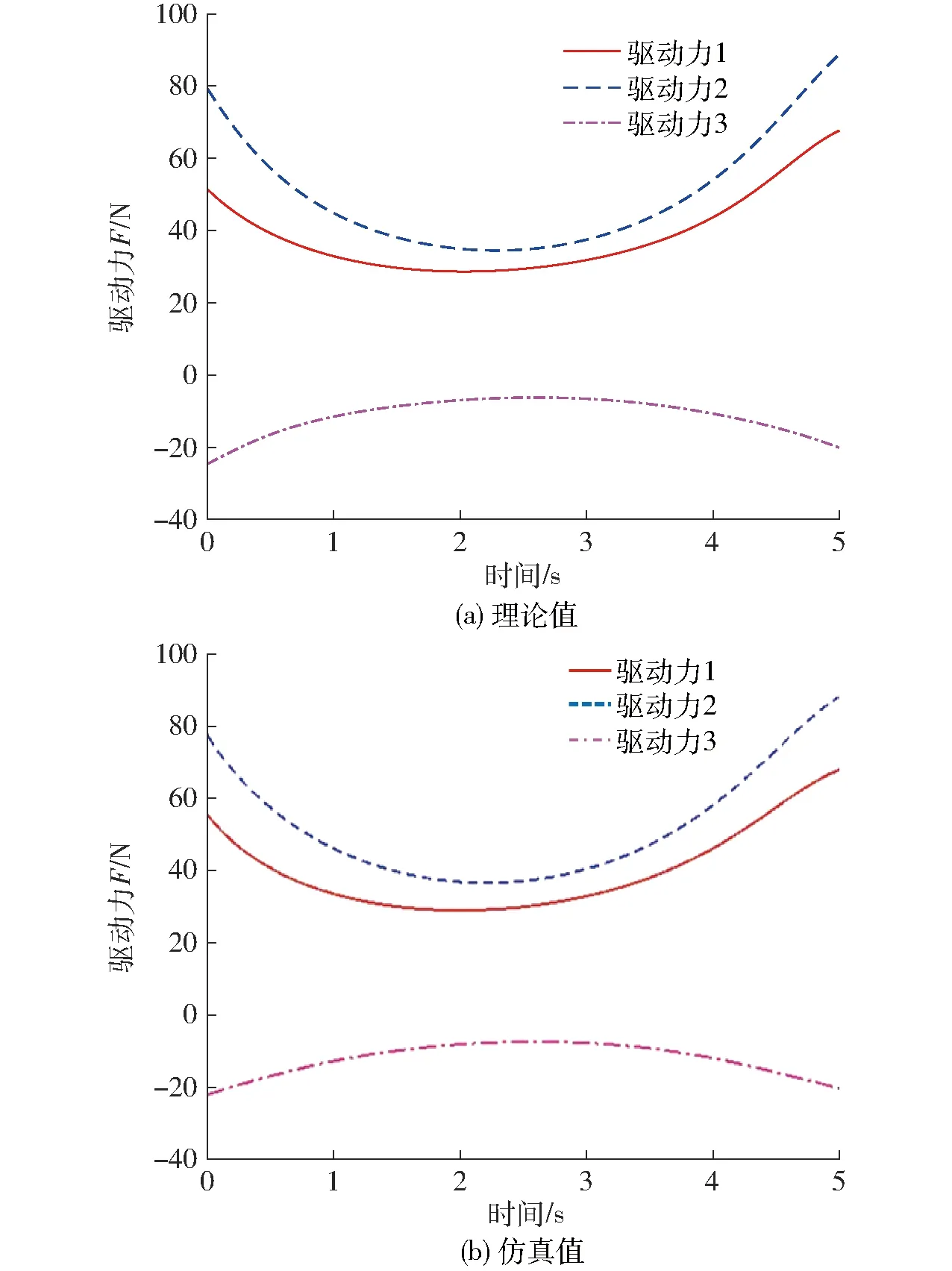
图12 2T1R并联机构驱动力曲线

而点D2支反力的理论值与仿真值如图13所示。

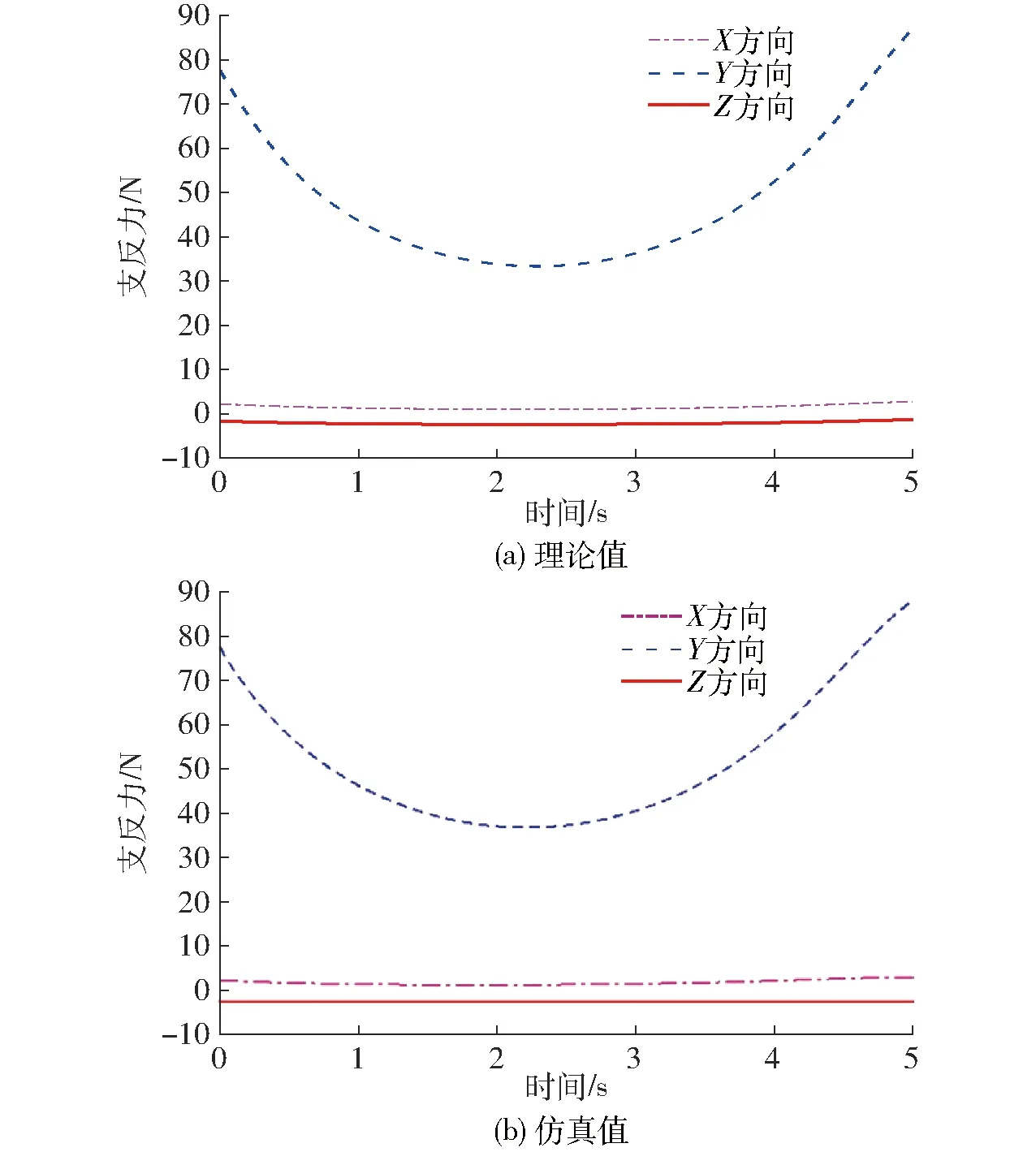
图13 点D2处支反力

由传统虚功原理可知

(i=1，2，…，12)

(41)

由式(41)可知，传统的虚功原理采用的是整体建模思想，而基于虚功原理的序单开链法则按照机构拓扑结构分解的顺序，分别建立各SKC的动力学模型，不仅建模思路清晰，而且使得机构的结构学、运动学以及动力学具有统一性。同时，可以得到不同SKC连接处运动副的支反力，有助于后续机构结构设计。

6 应用场景概念设计

该机构可用于物流领域两条平行布置、相距较远输送带(E、F)之间的物料的自动输送、转运和卸料，其平面示意图如图14a所示；该机构和输送带在空间的位置布置，以及送料、接料方式如图14b所示，图14c为其三维概念设计。

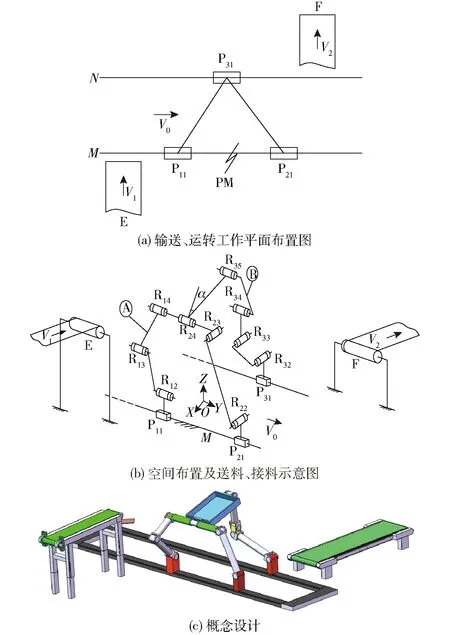
图14 用于物料输送与转运的3-DOF 2T1R并联机构

其工作原理是：当取静平台上的P11、P21和P31为主动副时，动平台1可实现YOZ平面内的两维平移以及绕R24轴线的一维转动，其中，两维平移(2T)能调整并联机构动平台1在Y、Z方向上的位移与输送带(E、F)的高度位置一致，而一维转动(1R)能使动平台1绕转动副R24轴线转动，从而使动平台1能适应自动接收来自输送带E上的物料，或将动平台1上的物料自动倾翻至输送带F上。