基于扩张观测器的HMCVT换段离合器油压跟踪控制

陆 凯 王 琳 鲁植雄 周华栋 钱 进 赵一荣

(1.南京农业大学工学院，南京 210031；2.拖拉机动力系统国家重点实验室，洛阳 471039)

0 引言

液压机械无级变速器(Hydraulic mechanical continuously variable transmission, HMCVT)结合了机械传动的高效和液压传动的平稳等优点，能够实现高效率、大功率的无级传动[1]，逐渐成为农业机械和工程车辆自动变速器的发展趋势。HMCVT通过控制湿式离合器实现段位切换，换段过程中离合器油压能否满足既定要求会影响摩擦副滑摩状态，进而影响换段品质[2-6]。

换段离合器液压控制系统作为机、电、液一体化的复杂非线性系统，具有未知干扰大、参数时变、非线性强等特点，因此换段离合器的油压跟踪控制仍是当前研究的热点和难点。目前，对换段离合器油压跟踪控制的研究主要集中在数学模型优化和控制方法改进两方面。JIAN等[7]使用粒子群算法对压力控制阀数学模型进行了优化，提高了离合器油压的稳定性。OUYANG等[8]提出了一种预测湿式离合器响应性能的方法，改善了油压控制效果。MESMER等[9]提出基于高精度模型的前馈控制策略和基于试验数据的神经网络控制策略，LAUKENMANN等[10]基于线性二次调节器设计了双自由度油压跟踪控制器，实现了离合器油压的跟踪控制。但上述研究对模型参数的精确度要求较高，且对未知干扰的鲁棒性较差。为了降低建模不准确的影响，增强控制系统的抗干扰能力，上官文斌等[11]计算了离合器机械、液压系统的传递函数，提出一种位置压力串级PID控制器，实现了离合器油压跟踪控制。傅生辉等[12]基于紧格式动态线性化提出了一种离合器油压无模型自适应预测控制算法，通过仿真证明了该算法的鲁棒性。PID控制结构简单，适应性强，但参数整定较为困难且存在超调和响应时间长等问题。无模型自适应预测算法需要在线滚动优化和反馈校正，对运算速度和控制器响应要求较高，且目前仅进行了仿真试验，未有实际控制结果。

相较于PID控制、自适应预测控制、神经网络控制等方法，滑模控制[13-16]对数学模型要求不高且具有较好的鲁棒性和稳定性，更适合于离合器油压跟踪控制。秦永峰等[17]提出了一种阀泵联合控制方法，并基于滑模控制设计了油压控制器，实现了离合器接合过程中油压的跟踪控制。李晓祥等[18]基于指数趋近律设计了自适应滑模控制器，实现了油压的跟踪控制，但滑模控制依然存在抖振和对不匹配干扰鲁棒性不强等问题。为此，LI等[19]在滑模控制器中加入了扰动观测器，该方法在一定程度上减弱了不匹配干扰的影响，但仍然存在抖振现象和收敛时间长等问题。

本文以装备在雷沃阿波斯大功率拖拉机上的三段式HMCVT换段离合器为研究对象，针对滑模控制中的未知干扰、抖振和收敛时间长等问题，设计一种基于扩张观测器的全局终端滑模控制器，以期提高HMCVT换段离合器油压跟踪控制的抗干扰能力和跟踪精度，并通过仿真和试验对控制器的性能进行验证。

1 HMCVT换段原理和动力学模型

1.1 HMCVT换段原理

三段式HMCVT传动原理如图1所示。发动机动力经PTO轴进入行星排，同时由传动比为i1的定轴轮系分流进入液压调速机构(包括变量泵和定量马达)，再经传动比为i2的齿轮进入行星汇流机构(包括P1、P2和P3行星排)，然后经过换段离合器(包括C1、C2和C3换段离合器)和换向离合器(包括CV前进离合器和CR后退离合器)实现动力输出，最终实现3个段位的无级变速。HMCVT通过调节排量比实现相邻两段的传动比连续变化，在相邻两段传动比交接点处进行换段称为同步换段。同步换段时控制目标段离合器的油压按照期望油压变化，可以减小换段冲击、降低离合器滑摩程度，从而提高换段平顺性和离合器寿命。

图1 HMCVT传动原理图

本文以第2段到第3段的同步换段为例，针对换段离合器油压控制存在的问题，设计基于扩张观测期的全局终端滑模算法的油压跟踪控制器，以期提高离合器的油压控制精度，改善换段品质。第3段换段离合器工作原理如图2所示。油泵泵出的油液经溢流阀后进入比例减压阀。当电磁线圈未通电时，比例减压阀阀芯在回位弹簧的作用下紧靠右端，进油口关闭，离合器油缸中残余油液通过卸油口流回油箱，离合器分离。电磁线圈通电时，电磁力推动比例减压阀芯左移，卸油口逐渐关闭，进油口开启，油液经油管进入离合器油缸，推动离合器活塞移动，离合器逐渐接合。

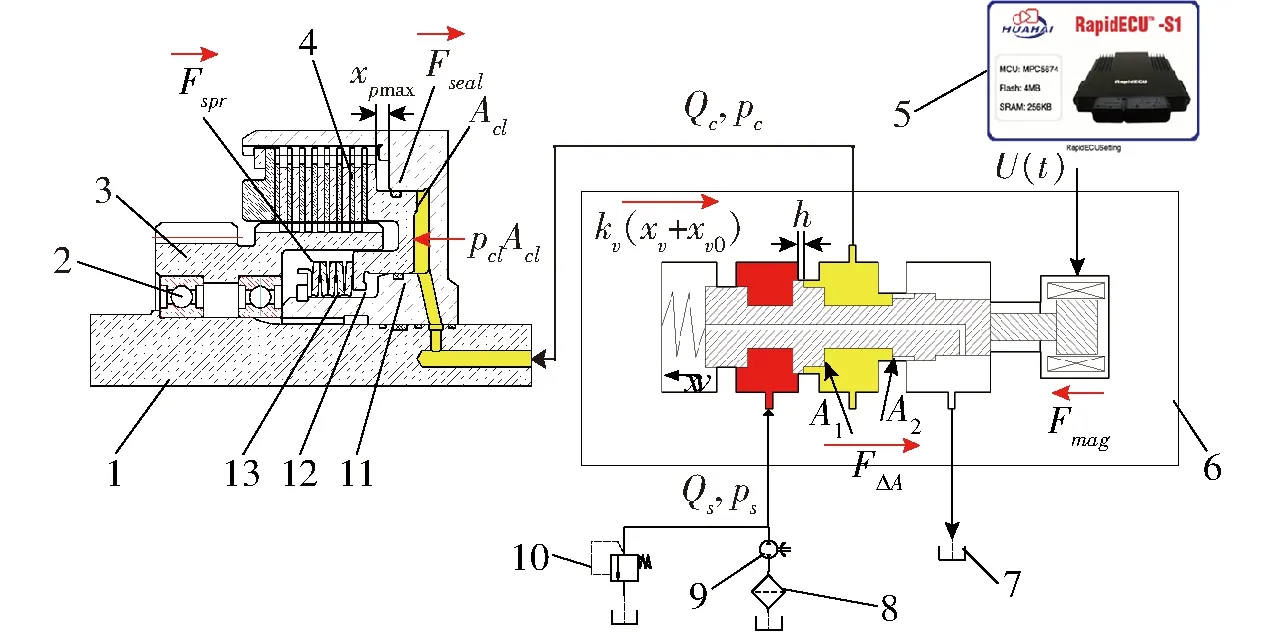
图2 HMCVT换段离合器工作原理图

1.2 换段离合器动力学模型

1.2.1比例减压阀动力学模型

(1)主阀芯受力平衡方程

比例减压阀的电磁线圈通电时，减压阀阀芯受到惯性力、阻尼力、弹簧力、电磁力、减压腔动压力等作用力，将阀参数摄动、油压摄动以及其它未建模参数引起的阀芯受力等效为未知扰动力，阀芯力平衡方程为

(1)

其中

(2)

式中mv——阀芯质量，kg

xv——阀芯位移，m

cv——阀芯运动阻尼系数，N·s/m

Fs——阀弹簧力，N

kv——阀弹簧刚度，N/m

xv0——阀芯初始位置弹簧压缩量，m

FΔA——减压腔静压力，N

Fd——未知扰动力，N

pc——减压腔油压，Pa

Fmag——电磁力，N

Ki——电磁力增益系数，N/V

U(t)——控制电压，V

A1——减压腔左端面积，m2

A2——减压腔右端面积，m2

(2)比例减压阀压力-流量方程

进入比例减压阀的油流量为

(3)

式中Qin——进入阀的油流量，m3/s

cd——阀流量系数

dv——进油口面积梯度，m

h——阀芯至开启位置的距离，m

ps——系统供油压力，Pa

ρ——液压油密度，kg/m3

xvmax——阀芯最大位移，m

(3)比例减压阀流量连续性方程

忽略比例减压阀配合间隙和接口处的泄漏，进入比例减压阀的油液补偿完压缩量后全部进入离合器油缸，则

(4)

式中Qcl——离合器油缸流量，m3/s

Vv0——比例减压阀减压腔体积，m3

E——油液体积弹性模量，Pa

1.2.2湿式离合器动力学模型

忽略液压油在油道内的阻力，离合器活塞的力平衡方程为

pclAcl-Fseal+Fw-Fcl

(5)

其中

(6)

式中m——活塞质量，kg

cp——粘度阻力系数，N·s/m

kp——回位弹簧刚度，N/m

xp——活塞位移，m

xp0——离合器弹簧初始压缩量，m

Acl——活塞面积，m2

Fseal——活塞密封圈阻力，N

Fw——液压油离心力，N

Fcl——摩擦副受到的正压力，N

μs——密封圈摩擦因数

b——密封圈宽度，m

r1——活塞外半径，m

r2——活塞内半径，m

R1——摩擦片外半径，m

R2——摩擦片内半径，m

pcl——离合器油缸油压，Pa

ω——离合器旋转角速度，rad/s

Tcl——离合器扭矩，N·m

z——摩擦副数量

μf——摩擦因数

忽略离合器活塞密封圈和旋转管接头的泄漏，进入离合器的流量连续方程为

(7)

其中

V0=Vc0+Vv0

(8)

式中V0——减压腔与油缸初始体积和，m3

Vc0——离合器油缸初始体积，m3

2 基于扩张观测器的换段离合器油压全局终端滑模控制器设计

2.1 湿式离合器油压控制系统状态方程

对油压进行控制的目的在于使离合器传递的扭矩能够满足既定要求，而离合器接合过程中的扭矩传递是在建压阶段，因此本文针对建压阶段设计基于干扰观测器的全局终端滑模控制器跟踪控制离合器油压。忽略减压阀动态特性和时间常数[20]，可将减压阀阀芯运动过程看作是恒速的，由式(1)得简化后的减压阀阀芯运动方程为

(9)

建压阶段，减压阀减压腔油压与离合器油缸油压相同，即pc=pcl。活塞达到最大位移xpmax，运动速度为零。由式(1)～(9)可得油压变化率与控制电压输入的关系为

(10)

(11)

其中

d1、d2为未知干扰，具有连续可导性，且有|d1|≤D1、|d2|≤D2，D1、D2为大于零的正实数。

2.2 扩张干扰观测器设计

根据干扰项是否在控制信道内将其分为匹配和不匹配干扰，因此在控制信道内的未知干扰d2为匹配干扰，不在控制信道内的未知干扰d1为不匹配干扰。终端滑模控制(Terminal sliding mode control, TSMC)对控制信道内的匹配干扰具有完全的鲁棒性，而对于不匹配干扰鲁棒性较弱。因此针对不匹配干扰d1设计二阶扩张干扰观测器[21]

(12)

2.3 全局终端滑模换段离合器油压控制器设计

传统终端滑模控制将非线性函数引入滑模面中，因而不含切换项，可以有效抑制抖振。一种TSMC滑动模态表达式为

(13)

式中s(x)——滑模面

β——非线性参数

p、q——正奇数，p>q

非线性函数可以有效增加系统向平衡态(x=0)收敛的速度，并且越远离平衡态，收敛速度越快。但当系统状态接近平衡态时，非线性滑模面比线性滑模面(p=q)需要更长的收敛时间。因此，全局终端滑模控制算法是在TSMC中引入线性项，使系统在远离平衡态时按照指数规律快速收敛到平衡态附近，接近平衡态时以线性规律收敛，其滑动模态为

(14)

式中α——线性参数

针对湿式离合器油压跟踪控制，定义湿式离合器油压积分曲线跟踪误差为s0，引入扩张观测器后，离合器油压系统滑动模态的递归结构可写为

(15)

式中xd——期望油压的积分值

s1——滑动模态函数

对s1求导，得

(16)

由式(12)可得

(17)

设计趋近律为

(18)

将式(17)、(18)代入式(16)得控制规律U(t)为

(19)

为了保证控制器的收敛性和鲁棒性，定义Lyapunov函数为

(20)

根据Lyapunov稳定性理论，由式(20)可知，本文所设计的湿式离合器油压跟踪控制器对匹配干扰具有鲁棒性，整个控制系统渐进稳定。

3 换段离合器油压跟踪控制仿真与试验

3.1 油压跟踪控制仿真分析

基于Matlab/Simulink建立了离合器液压系统、全局终端滑模控制器、扩张观测器模型，通过仿真验证全局终端滑模控制算法的有效性和稳定性，控制系统原理如图3所示。

图3 换段离合器油压跟踪控制系统原理图

扩张观测器和滑模控制器参数取值为：α0=5 000，β0=1，p0=11，q0=7，α1=60，β1=5，p1=11，q1=7，b1=2 000，b2=400。HMCVT换段离合器油压控制系统的参数见表1。

表1 换段离合器油压控制系统参数

为验证全局终端滑模控制的控制效果，首先在无干扰条件下，分别使用全局终端滑模控制和TSMC对期望油压进行跟踪控制，结果如图4所示。

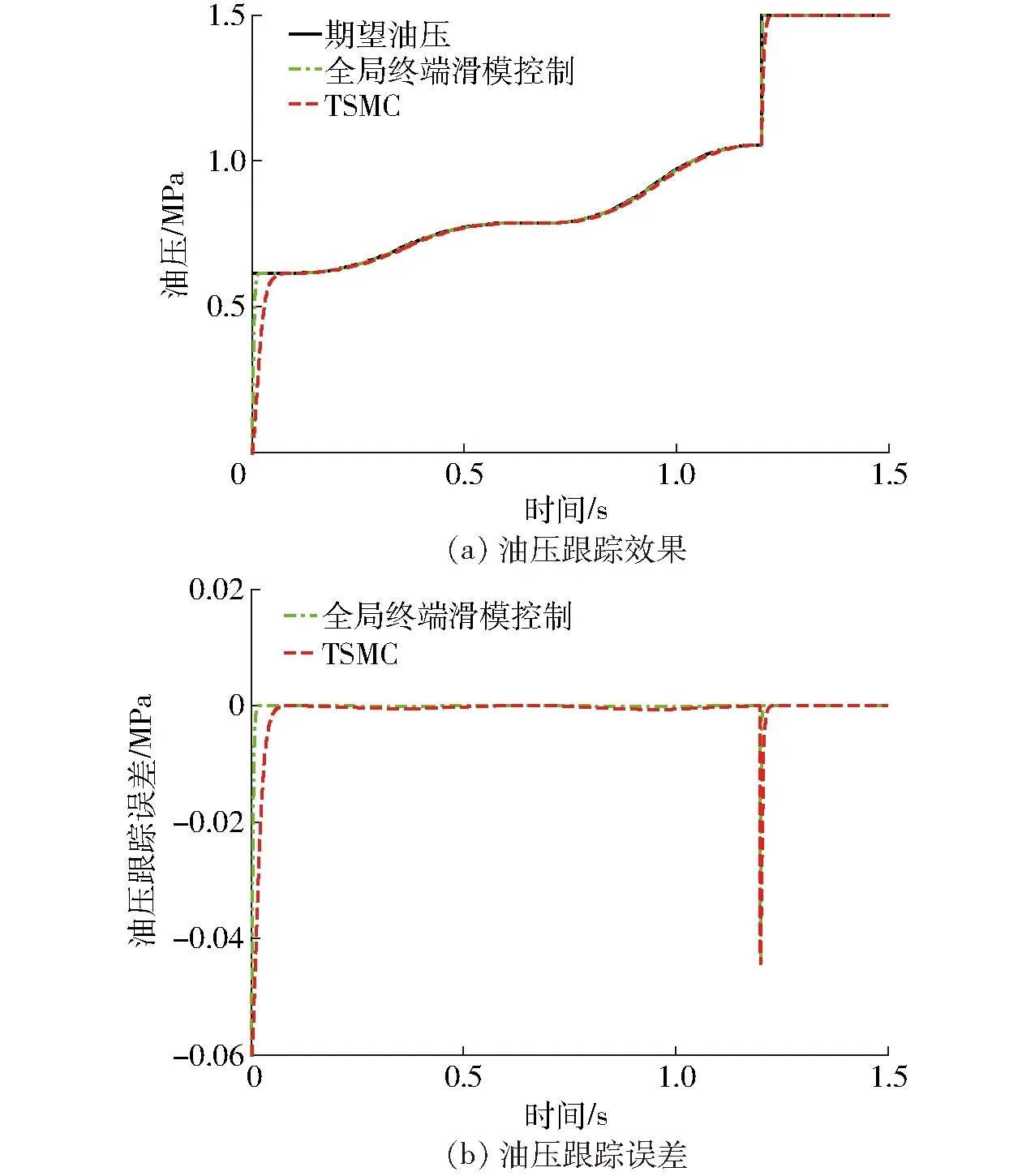
图4 无干扰离合器油压跟踪控制结果

从图4a可得，两种方法都能实现离合器油压的跟踪控制，但全局终端滑模控制的响应时间较TSMC快0.07 s。从图4b可得，两种方法的最大跟踪误差都发生在1.2 s处，最大瞬态跟踪误差为0.042 MPa。这是因为在1.2 s时期望油压发生阶跃上升达到系统油压，由于系统惯性的影响使两种方法产生了较大瞬时误差。而在0.08～1.2 s时间内，全局终端滑模控制的最大跟踪误差为期望油压的0.17%，TSMC的最大跟踪误差为期望油压的0.87%。因此，本文所提全局终端滑模控制与TSMC相比，在响应时间和跟踪精度上具有优越性。

然后为验证扩张观测器对不匹配干扰的估计效果，在离合器油压控制系统中引入随机不匹配干扰，扩张观测器对干扰的估计结果如图5所示。

图5 扩张观测器对不匹配干扰的估计结果

从图5看出，观测器最大瞬态误差为0.036 MPa，最大稳态误差为0.002 MPa，扩张观测器输出的估计干扰值与施加干扰值基本吻合。因此，将扩张观测器的估计值补偿到控制器中能够提高控制器精度。在控制器中加入扩张观测器后的控制结果如图6所示。

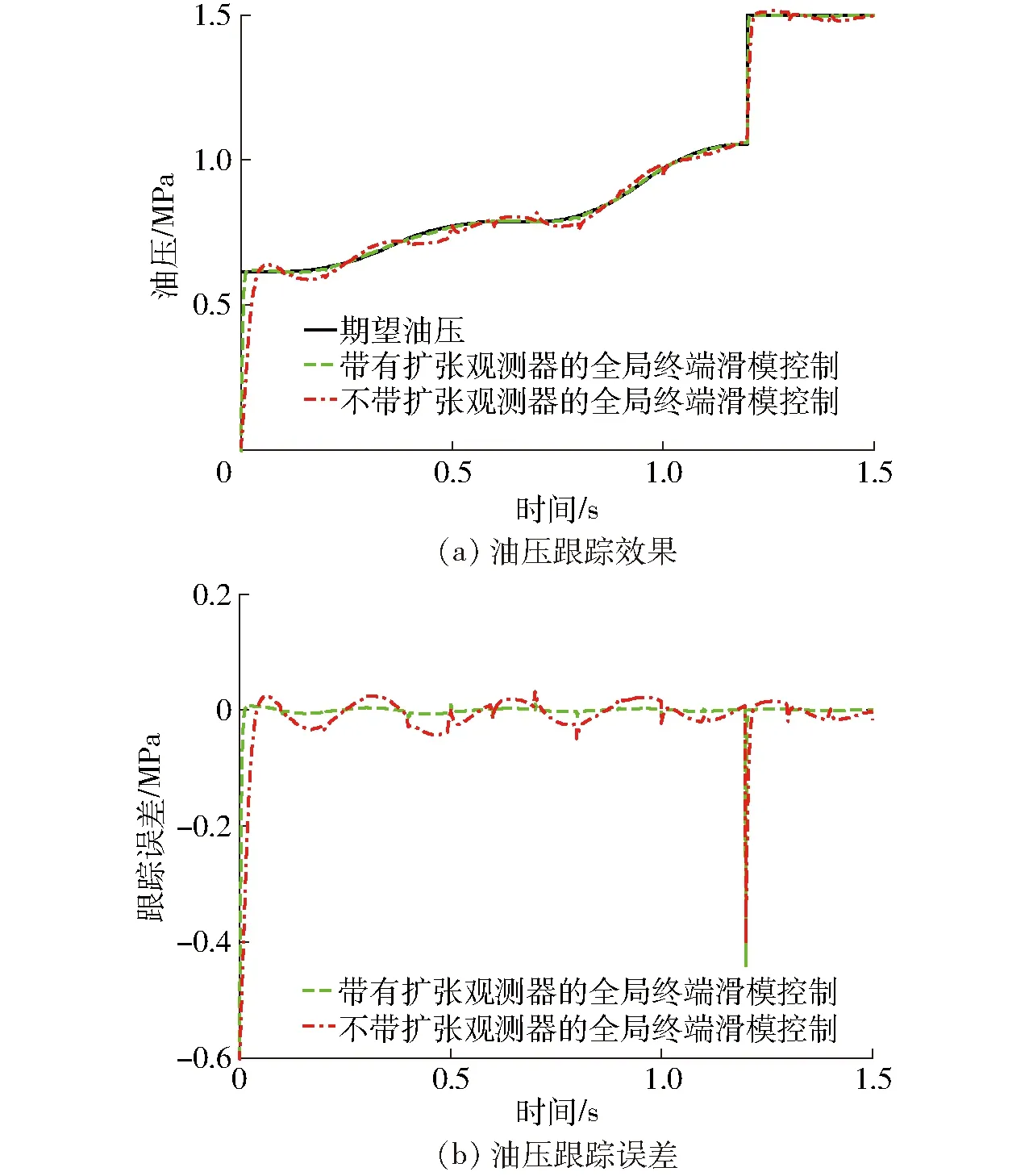
图6 有干扰换段离合器油压跟踪控制结果

由图6可知，无扩张观测器的油压跟踪效果受不匹配干扰影响较大，在系统响应初期存在6.5%的超调量，且整个油压跟踪过程出现明显抖振。加入扩张观测器后的全局终端滑模控制油压跟踪控制系统响应初期的超调量3.6%，跟踪过程无明显抖振。因此，在控制器中加入扩张观测器能够有效补偿不匹配干扰造成的控制误差，提高控制精度。

3.2 换段离合器油压跟踪控制试验分析

3.2.1试验台架

为了验证本文所设计油压跟踪控制器的实际可行性，搭建了HMCVT换段离合器油压控制试验台架，如图7所示。试验台架由一台变频电机驱动，型号YXVE315L2-4，额定扭矩1 286 N·m，调速范围0～1 450 r/min。通过德力西变频器调整电机输出功率。兰菱机电ZJ-A型转速转矩传感器转速量程0～3 000 r/min，转矩量程0～2 000 N·m。转动惯量盘等效转动惯量为1.96 kg·m2。加载装置为兰菱机电电涡流制动器，型号CWC2000，集成了转速传感器和转矩传感器。油压传感器为建胜油压变送器，型号JPL131，量程0～10 MPa。湿式离合器箱包含湿式离合器及其传动齿轮，齿轮减速比为1.29。测控计算机包括上位机和数据采集设备，其中控制器程序使用LabView编写，数据采集设备为NI公司的USB-6535。比例减压阀为上海立新公司的电磁比例减压阀。

图7 HMCVT换段离合器油压控制试验台

3.2.2油压跟踪试验

以拖拉机使用五铧犁进行浅耕作业为例，分别在耕深为8、13、18 cm共3种工况下进行油压跟踪试验。浅耕时，忽略加速阻力、坡度阻力和空气阻力，拖拉机主要受到犁耕阻力和滚动阻力。其中犁耕阻力的计算公式为

Fq=nBhhdw

(21)

式中Fq——犁耕阻力，N

n——铧犁数量

B——土壤耕阻比，N/cm2

hh——耕深，cm

dw——耕作宽度，cm

滚动阻力计算公式为

Ff=fMg

(22)

式中Ff——滚动阻力，N

f——滚动阻力系数

M——拖拉机质量，kg

g——重力加速度，m/s2

根据动力传递路线，离合器负载扭矩与拖拉机阻力的关系为

(23)

式中rt——驱动轮半径，m

iw——轮边减速器减速比

i0——主减速器减速比

i8——输出轴传动比

雷沃阿波斯大功率拖拉机主要技术参数和土壤参数如表2所示。

将表2中数据代入式(21)～(23)可得3种耕深工况下的离合器负载分别为600、800、1 000 N·m，对应的期望油压曲线如图8所示。

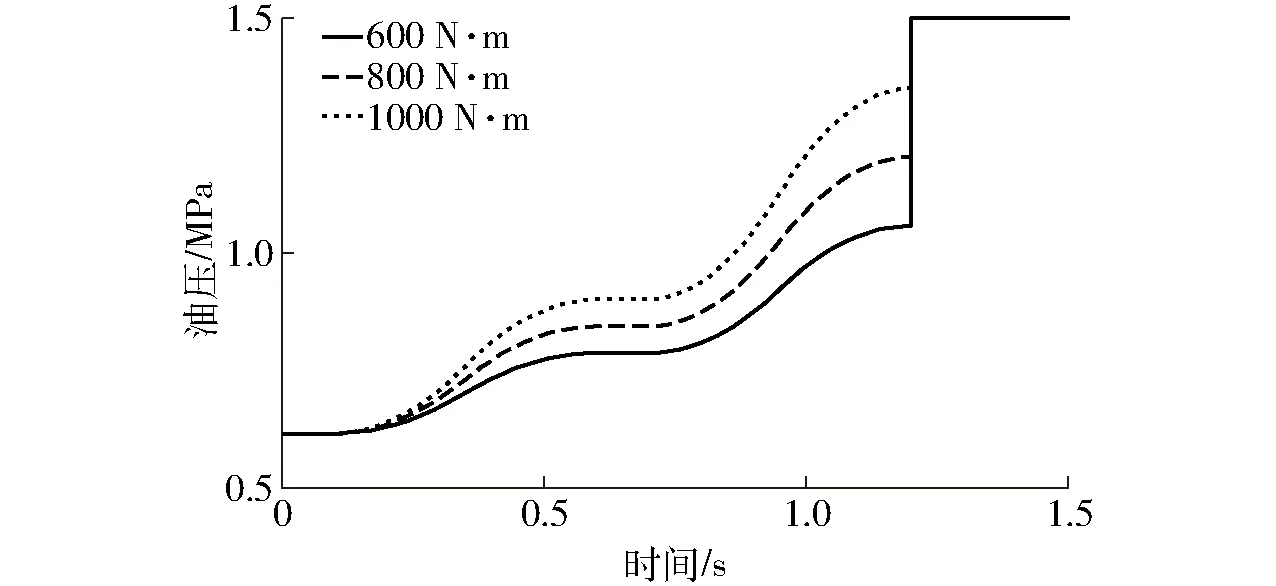
图8 不同负载下换段离合器的期望油压变化曲线

表2 拖拉机主要技术参数和土壤参数

试验时控制器参数与仿真参数设置相同，分别使用本文控制算法与TSMC对3种工况下的油压进行跟踪对比试验，油压跟踪结果和控制器电压输出如图9、10所示。

图9 3种工况下换段离合器油压跟踪控制试验结果

图10 换段离合器控制器输出电压变化曲线

比较油压跟踪结果和控制器输出电压可知，本文算法和TSMC在油压响应初期均存在一定的时延，这是受控制器数据传输速度限制和液压系统惯性的影响，但本文算法油压响应时延为0.03 s，较TSMC快0.02 s，具有更好的系统适应性。在跟踪油压过程中，TSMC在负载600 N·m下存在 0.24 MPa的超调量，而本文算法最大超调量产生在负载 800 N·m条件下，仅为0.08 MPa。另外，本文算法的最大油压上升稳定时间(偏离目标值±2%范围)为0.13 s，较TSMC快0.24 s。说明本文算法的系统适应性和动态响应较TSMC好。

另外，从控制器电压输出结果可知，TSMC的电压输出产生了较为明显的抖振，本文算法则无明显抖振，说明本文算法对于不匹配干扰的抑制能力较强，与仿真结果一致。根据油压跟踪结果，抖振的产生使TSMC在油压阶跃阶段(11.7～12 s)的响应时间产生了一定滞后并存在一定的超调量，这一现象在负载800、1 000 N·m条件下尤为明显，但由于负载的增加使阶跃量减小，同时使TSMC的超调量也随之减小，而本文算法在此阶段无明显抖振和超调。综上所述，本文算法与TSMC相比具有更好的系统适应性和鲁棒性。

3.2.3浅耕作业换段试验

为了进一步验证本文算法的优越性，通过台架模拟HMCVT第2段到第3段的同步换段过程。以冲击度和滑摩功作为评价离合器接合品质的评价指标，分析离合器换段平顺性。

设置离合器主动端转速为1 000 r/min，在离合器从动端分别施加负载600、800、1 000 N·m，然后在第30秒时分离第2段离合器，同时分别使用本文算法和TSMC控制第3段离合器按照期望油压接合。换段试验的冲击度和滑摩功如图11、12所示。

图11 不同条件下的冲击度对比

由图11可知，在负载600 N·m下本文算法的最大冲击度为-34.5 m/s3，较TSMC最大冲击度减小11.3%。随着负载的增大，两种算法的冲击度均在一定程度上降低，但本文算法在负载800、1 000 N·m下的最大冲击度仍比TSMC降低8.4%和12.7%，说明在不同的负载条件下，本文算法仍然具有较好的控制效果。

由图12可知，相同负载下本文算法和TSMC的滑摩时间基本相同，随着负载的增加滑摩时间也增加，滑摩功随之增加。在负载600、800、1 000 N·m下本文算法的滑摩功为1.26、2.98、8.46 kJ，较TSMC分别减少6.0%、10.2%和1.3%。由于负载1 000 N·m下的滑摩功主要由受滑摩时间和主从动角速度差的影响，离合器扭矩的偏差对滑摩功影响不明显，因此在该负载下本文算法与TSMC算法滑摩功差别不大。总体来说，本文算法的HMCVT换段冲击度和滑摩功均小于TSMC，本文算法在HMCVT换段品质方面更具优越性。

图12 不同条件下的换段离合器滑摩功对比

4 结论

(1)针对HMCVT换段离合器油压控制系统特点，提出了一种带有扩张观测器的全局终端滑模控制算法。通过在TSMC中引入线性项提高滑模控制的收敛速度，通过设计扩张观测器抑制不匹配干扰造成的抖振，提高了控制器的响应特性和稳定性。

(2)基于Matlab/Simulink进行了控制器仿真，结果表明TSMC引入线性项后控制器的响应时间缩短0.07 s。扩张观测器的最大稳态误差仅为0.02 MPa，能够实现不匹配干扰的有效估计。将扩张观测器估计值补偿到控制器中能够有效降低抖振和系统超调量。

(3)在负载600、800、1 000 N·m下，分别使用本文算法和TSMC进行的油压跟踪控制试验和离合器接合品质试验结果表明，本文算法无明显抖振，动态响应时间仅为0.13 s，油压超调量仅为0.08 MPa，换段冲击度最大降低12.7%，滑摩功最多减少10.2%。说明本文所提算法具有较好的鲁棒性，能够为HMCVT换段离合器油压跟踪控制提供参考。