基于圆筒入渗仪的田间膜孔灌土壤入渗参数研究
2023-03-07范严伟唐兴鹏史金红马天花
范严伟 唐兴鹏 史金红 马天花
(兰州理工大学能源与动力工程学院,兰州 730050)
0 引言
地膜覆盖是中国干旱、半干旱地区常用的栽培技术[1-2]。膜孔灌是在地膜覆盖基础上发展起来的一种地面灌溉技术,其灌溉过程中,水在地膜上传输并通过作物孔或专用灌水孔(统称为膜孔)渗入根区土壤,具有节水、增温、保墒等优点[3-4]。该灌溉方式投资少、效益高且简便易行,在农业节水灌溉领域具有良好的应用前景。
膜孔入渗规律研究是优化田间膜孔灌灌水技术要素的基础,而土壤入渗参数的准确估算是量化表征膜孔入渗规律的关键[5]。目前,对膜孔灌土壤入渗参数的研究主要集中在室内试验[6-8]和数值模拟[9-11]两方面。室内试验能够较好地控制灌水技术要素,如土壤质地、容重和初始含水率以及膜孔直径和灌溉水头等,是揭示膜孔入渗规律的基本方法,但室内试验所用土壤多为扰动土且质地类型较单一,导致试验推求的土壤入渗参数普适性不强;数值模拟能够快速全面地获取不同灌水要素组合下土壤水分运动规律,是定量分析膜孔入渗特性的有效手段,但基于数值模拟结果构建的相关估算模型还需试验数据的验证。为此,一些学者采用数值模拟和试验验证相结合方法,开展了膜孔灌土壤湿润体特性研究,如介飞龙等[12]基于HYDRUS模拟结果,建立了考虑土壤初始含水率和特征(水平和垂向)湿润距离的累积入渗量模型,并利用室内试验进行了验证。由于模型中包含了特征湿润距离这一待测值,使其在田间实际应用中受到限制,因为田间膜孔灌土壤表面覆有地膜,其特征湿润距离难以观测;FAN等[13]在数值分析影响湿润体运移的主导因素的基础上,建立了包含土壤饱和导水率、膜孔直径和灌水时间的特征湿润距离估算模型。该模型的建立是基于HYDRUS软件中自带的土壤质地类型,未考虑土壤容重的影响,另外将土壤饱和导水率考虑其中,而田间测定原状土饱和导水率相对较麻烦[14-16]。因此,有必要发展一种能够对田间膜孔灌湿润体尺寸进行现场评估的新模型、新方法。
为体现土壤质地的广泛性和研究成果的普适性,本文依据国际制土壤质地分类标准配置12种土壤质地类型,在测定大量土壤水力特性参数的基础上,采用HYDRUS-2D/3D模拟研究土壤容重和膜孔直径对12种质地土壤入渗特性的影响;基于数值模拟结果,对湿润体运移模型的参数进行优化,进而提出一种新的膜孔灌湿润体尺寸估算模型;设计一种反映田间膜孔灌入渗过程的试验装置,用于验证估算模型的可靠性,实现估算模型在田间的实际应用,为设计运行管理人员提供简便的实用工具。
1 材料与方法
1.1 技术路线
首先,设计一种真实反映田间膜孔灌入渗过程的试验装置——圆筒入渗仪;其次,利用圆筒入渗仪田间试验验证HYDRUS-2D/3D模拟结果的准确性,在此基础上,模拟研究不同影响因素下膜孔灌土壤入渗率和湿润体尺寸变化规律;然后,基于180组数值模拟结果,优化确定膜孔灌土壤湿润体运移模型参数;最后,采用田间圆筒入渗仪试验和室内土箱试验评价模型的可靠性,实现膜孔灌湿润体运移模型在田间的实际应用。具体技术路线如图1所示。
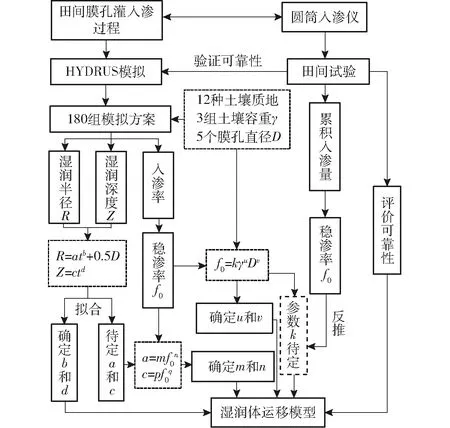
图1 技术路线图
1.2 膜孔灌田间试验设计
根据田间膜孔灌特点,设计了一种能够真实反映膜孔入渗过程的圆筒入渗仪,如图2所示。该仪器类似于圭尔夫(Guelph)入渗仪,利用马氏瓶原理提供恒定水头,但圆筒入渗仪将供水单元与渗水单元一体化,试验前无需组装调试,操作方便;试验前圭尔夫入渗仪需钻孔打洞,这无法反映土壤表面膜孔入渗情景,而圆筒入渗仪无需钻孔,仅竖直放于待测土壤之上即可,可真实反映地膜覆盖下膜孔入渗情景;另外圆筒入渗仪采用有机玻璃粘接而成,制作简单,成本低廉。
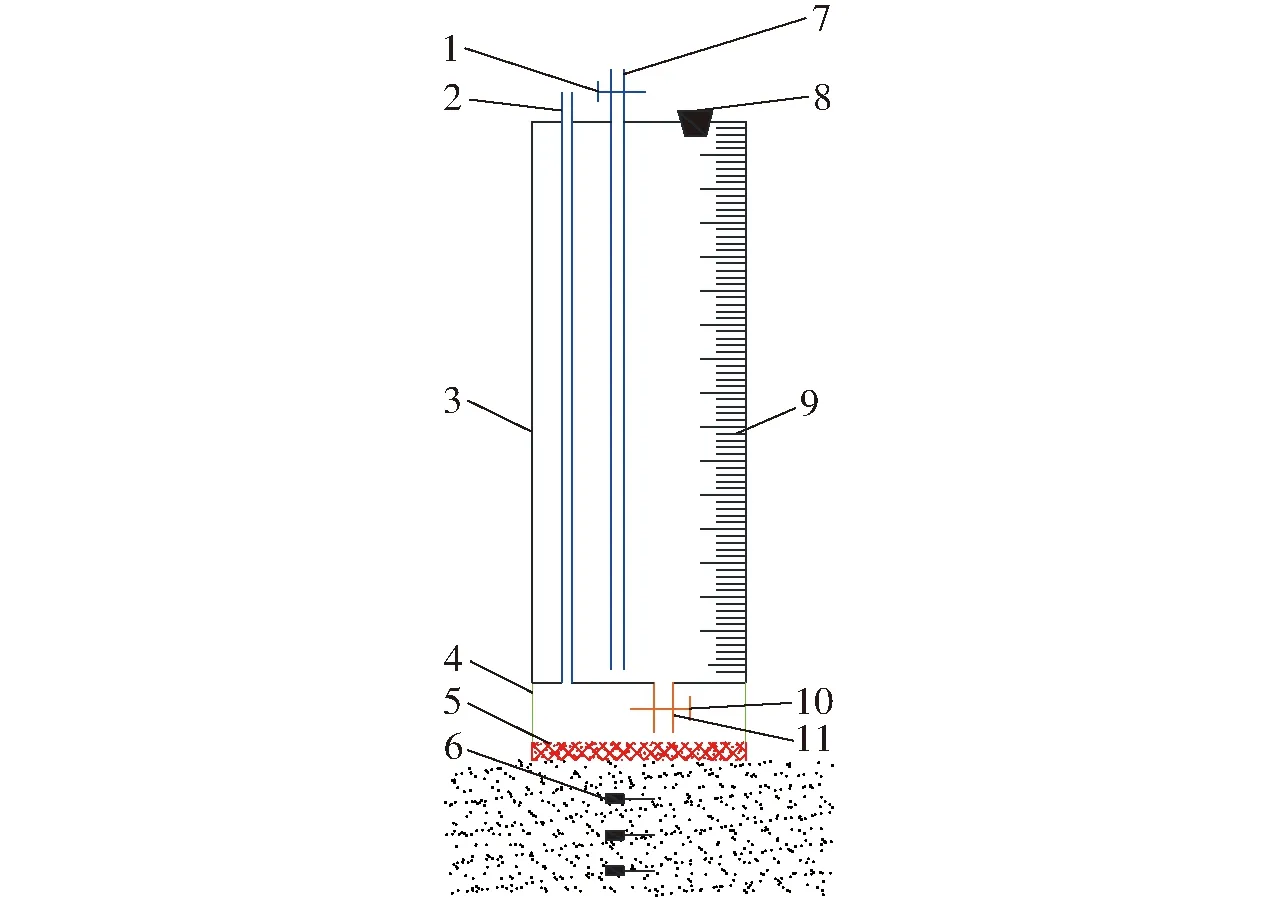
图2 圆筒入渗仪田间试验示意图
圆筒入渗仪供水单元由储水室和进气管组成,进气管一端通过进气阀与大气相通,另一端伸入储水管直至底部,用于控制入渗室保持恒定水头;渗水单元由入渗室、排气管、出水管和透水垫组成,入渗室相当于膜孔装置,排气管用于试验初期入渗室空气的排出,透水垫可防止出水管水流对地面的击溅。田间试验具体操作步骤为:①选择待测区域,确定待测地点,然后去除待测点地表的植被及石块等大体积杂物,将地面整平。②关闭进气阀和出水阀,通过橡胶塞孔往储水室加满水。③封闭橡胶塞,打开出水阀,直至储水管水位稳定,将圆筒入渗仪竖直放入待测地点。④记录储水管初始水位,打开进气阀,记录不同时刻水位变化,待变化速率基本稳定时,停止试验。通过以上4步即可确定膜孔稳渗率,进而推求土壤入渗参数,整个试验过程中土壤无扰动。需要说明的是,文中所建湿润体运移模型的验证部分,需将水分传感器埋入土中并回填土,为了减少土壤扰动产生的试验误差,待回填土与原土物理性质基本相同后再开展试验,并增列步骤⑤,即:⑤在步骤④过程中,观测不同时刻地表湿润半径,而垂向湿润深度通过圆筒入渗仪下方水分传感器获得,记录水分达到传感器的时间。
1.3 膜孔灌数值模拟
1.3.1基本方程
假设土壤是均质且各向同性的,膜孔灌土壤水分运动可简化为轴对称二维入渗问题。采用HYDRUS-2D/3D软件[17]进行模拟,其基本方程为Richards方程,即
(1)
式中θ——土壤体积含水率,cm3/cm3
t——时间,min
r——径向坐标,cm
h——压力水头,cm
z——垂向坐标,规定向下为正,cm
K(h)——土壤非饱和导水率,cm/min
通过VAN GENUCHTEN-MUALEM(VG-M)模型[18-19]来描述土壤水分特征曲线和土壤非饱和导水率,计算式为
(2)
(3)
式中Ks——土壤饱和导水率,cm/min
Se——土壤相对饱和度
θs——土壤饱和含水率,cm3/cm3
θr——土壤残余含水率,cm3/cm3
α——与进气值成反比的经验参数,cm-1
β——影响土壤水分特征曲线形状的经验常数
1.3.2定解条件
充分考虑田间膜孔灌实际情况,设定不同建模情景的初始和边界条件,如图3所示,图中S为膜孔间距,cm;θ0为土壤初始含水率,cm3/cm3;θc为田间持水率,cm3/cm3。

图3 膜孔灌土壤水分运动计算域示意图
为确保计算域边界设置与田间实际相符,考虑膜孔的对称性,以膜孔圆心为起点设置上边界和左边界;采用1/2膜孔间距作为右边界,需要说明的是,对于不同的田间植物,其膜孔间距不等,差异较大,文中边界设置主要是针对较大膜孔间距的自由入渗情景;对于下边界可设置垂向距离足够大(本文取100 cm),以满足模拟结束时刻不受灌水影响。在所有的模拟情景中,计算域内土壤水分均按初始含水率设置,根据文献[20-23]的田间适宜灌水下限范围(50%~70%田间持水率θc),本文按60%田间持水率设置;上边界AB为膜孔外围覆膜地表,不受蒸发和降水影响,按零通量边界设置;下边界CE不受灌水影响,按自由排水边界设置;左边界EF为膜孔中心线,无水量交换,按零通量边界设置;右边界BC灌溉水分未达到,按零通量边界设置;边界AF为上方有水头的膜孔区,考虑田间膜孔上方水头(2~10 cm)难以控制且对土壤入渗影响较小,为简化计算,本文按水头6 cm定边界设置。
综上所述,初始条件可描述为
(4)
式中Ω——计算域(图3)
最终边界条件可总结为
(5)
式中H——膜孔上方水头,cm
1.3.3模拟方案
参照国际制土壤质地分类标准,配置4个类别12种土壤[24]。将每种土壤设置3组容重(γ),通过离心机法测定土壤水分特征曲线,RETC拟合确定θs、θr、α和β,定/变水头法测定Ks,环刀法测定θc,相关参数见表1。在H=6 cm、θ0=60%θc情况下,设置180种情景(12种土质、3组容重、5个膜孔直径),模拟分析土壤容重和膜孔直径对12种质地土壤入渗率和湿润体尺寸的影响。
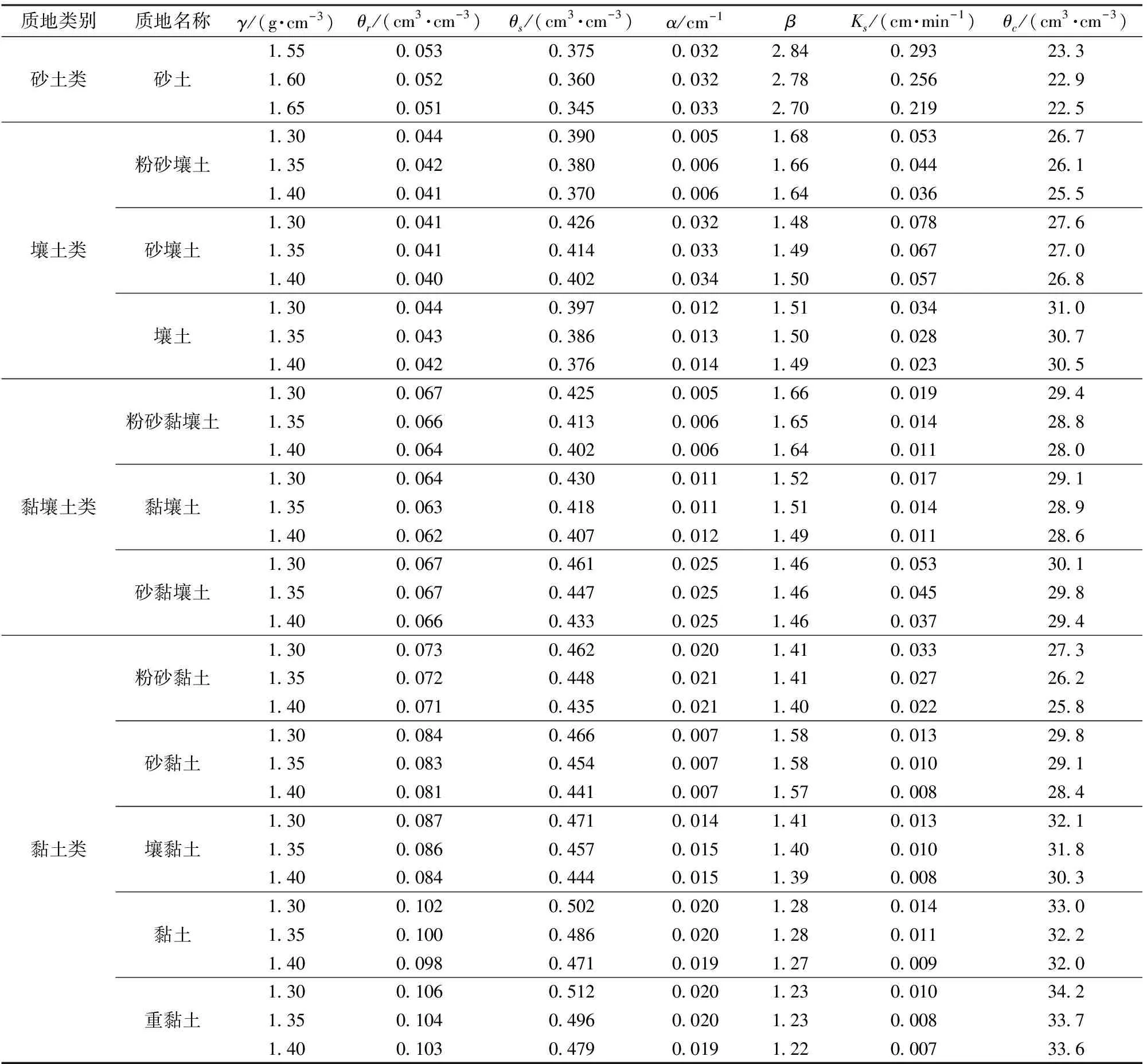
表1 不同容重下12种土壤质地VG-M模型参数和田间持水率
1.4 膜孔灌湿润体运移过程描述
膜孔入渗过程中土壤湿润体形状近似于半椭球体,其特征轴为水平向湿润半径R和垂直向湿润深度Z,两者与时间具有良好的幂函数关系[5,7,13],表达式为
R=atb+0.5D
(6)
Z=ctd
(7)
式中a、b、c、d——入渗参数
1.5 误差分析
为了验证估算模型可靠性,采用均方根误差(RMSE)和纳什效率系数(NSE)对估算值和实测值进行误差分析。当NSE越趋近于1,RMSE越靠近于0,说明估算值越接近于实测值,模型精度越高。
2 结果与分析
2.1 HYDRUS-2D/3D数值模拟验证
采用HYDRUS-2D/3D软件模拟获得粉壤土(D=8 cm、γ=1.33 g/cm3)不同时刻土壤入渗率和湿润距离,将模拟结果与圆筒入渗仪田间试验数据进行对比,如表2所示。
由表2可知,不同时刻土壤入渗率和湿润距离模拟值与实测值相对误差绝对值介于1.56%~9.09%之间,平均值为4.45%;入渗率的均方根误差为0.196 mL/min,纳什效率系数为0.992;湿润距离(湿润半径、湿润深度)的均方根误差为0.181 cm,纳什效率系数为0.990。说明文中所建数学模型是正确的,采用HYDRUS-2D/3D软件模拟田间膜孔灌入渗过程可靠。
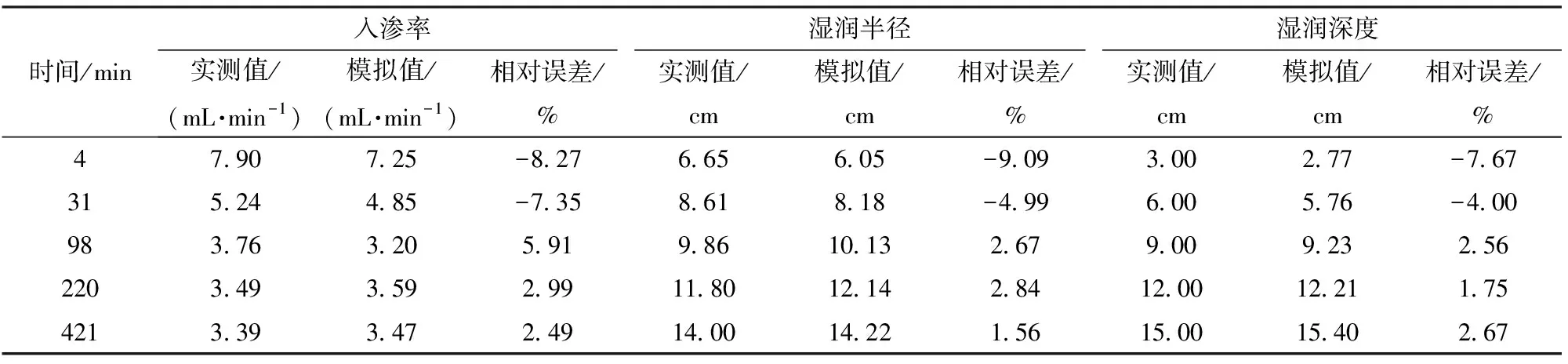
表2 土壤入渗率和湿润距离模拟值与实测值对比
2.2 不同影响因素对入渗率的影响
在相同土壤初始含水率(θ0=60%θc)和灌溉水头(H=6 cm)情况下,选定4种具有代表性的质地土壤(砂土、壤土、黏壤土、黏土)进行数值分析。图4为不同土壤容重和膜孔直径组合下4种质地土壤入渗率变化规律。

图4 不同土壤容重和膜孔直径组合下4种质地土壤入渗率变化曲线
由图4可知,不同影响因素组合下土壤入渗率随时间的变化规律相同,20组入渗率变化曲线都存在快速入渗和稳定入渗两个阶段,土壤质地越黏重,达到稳渗阶段的用时越长,但基本在120 min后进入稳渗状态。土壤质地对入渗率影响非常显著,相同条件下,砂土的稳渗率明显大于壤土、黏壤土和黏土,表现出土壤质地越黏重,土壤稳渗率越小的现象;土壤容重和膜孔直径均对入渗率有较大影响,相同条件下,稳渗率随膜孔直径增大而增大,随土壤容重增大而减小。这是因为膜孔直径越大,土壤受水面积越大,单位时间内入渗水量越多,使稳渗率随之增大;土壤容重越大,土壤渗透能力越弱,单位时间内入渗水量越少,导致稳渗率降低。
2.3 不同影响因素对湿润体运移的影响
2.3.1土壤容重对湿润体运移的影响
在θ0=60%θc、H=6 cm和D=6 cm情况下,对4种质地土壤(砂土、壤土、黏壤土和黏土)容重变化下的湿润体特征值进行数值分析,其中砂土容重为1.55、1.60、1.65 g/cm3,其他土质取1.30、1.35、1.40 g/cm3。图5为不同土壤容重条件下4种质地土壤的湿润体运移曲线。

图5 不同容重下4种质地土壤湿润体运移曲线
由图5可知,湿润半径和湿润深度均随时间的延长而逐渐增大,土壤质地越黏重,湿润体运移越缓慢。如灌水结束(240 min)时,容重为1.35 g/cm3的壤土、黏壤土和黏土的湿润半径分别是砂土(γ=1.60 g/cm3)的0.49、0.39、0.26倍,而湿润深度仅为0.35、0.27、0.17倍,说明土壤质地对湿润体运移有显著影响,在灌溉系统设计中土壤质地是必须要考虑的。对于同一土壤质地,湿润半径和深度均随容重的增加而减小。以壤土为例,灌水结束时容重为1.35、1.40 g/cm3的湿润半径比1.30 g/cm3的分别减小7.3%和13.7%,而湿润深度分别减小7.7%和14.6%,说明土壤容重变化会影响湿润体运移过程,在灌溉系统优化设计中也是应该考虑的影响因素。
2.3.2膜孔直径对湿润体运移的影响
选取容重为1.60 g/cm3的砂土以及容重为1.35 g/cm3的壤土、黏壤土和黏土,在θ0=60%θc和H=6 cm情况下,对4种质地土壤膜孔直径变化(D=4、6、8 cm)下的湿润体特征值进行数值分析。图6为不同膜孔直径条件下4种质地土壤的湿润体运移曲线。
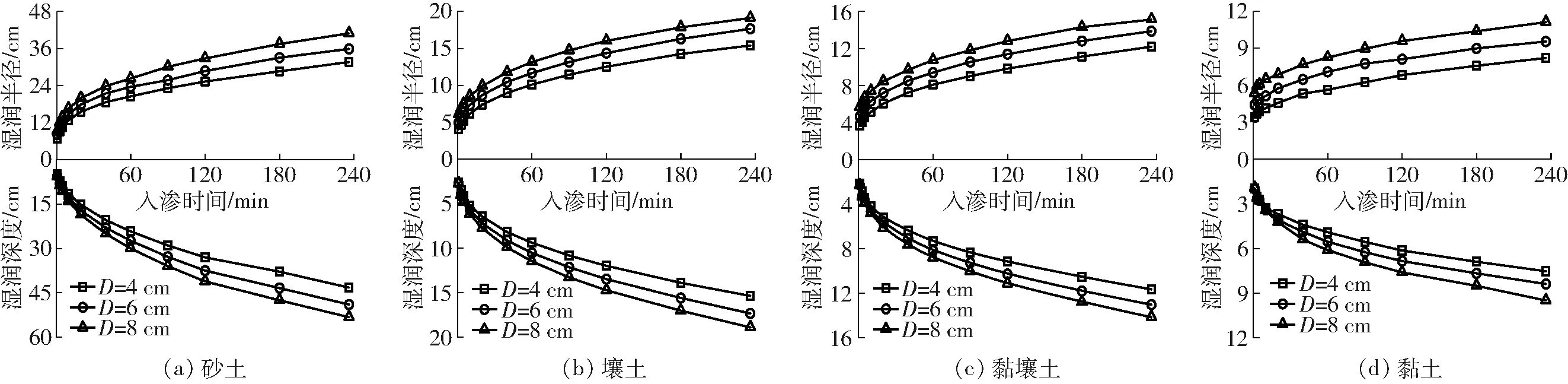
图6 不同膜孔直径下4种质地土壤湿润体运移曲线
由图6可知,土壤质地差异对湿润半径和深度的影响规律与图5相似,两个方向上湿润体运移距离由大到小表现为砂土、壤土、黏壤土、黏土。相同土壤质地和容重条件下,湿润半径和深度均随膜孔直径的增大而增大。以D=4 cm为基准,灌水结束时壤土的湿润半径和湿润深度分别为15.48 cm和15.36 cm,当膜孔直径增至6 cm和8 cm时,湿润半径分别增加14.5%(2.25 cm)和26.8%(4.15 cm),湿润深度分别增加12.8%(1.96 cm)和23.0%(3.53 cm),说明膜孔直径对湿润体运移存在较大影响,是膜孔灌系统中非常重要的技术参数。
2.4 膜孔灌湿润体运移模型建立
通过数值分析膜孔灌湿润体运移影响因素可知:土壤质地、膜孔直径、土壤容重和灌水时间均会对湿润半径和湿润深度产生影响,是不容忽视的主导因素。因此,基于180组模拟结果,利用式(6)和式(7)拟合获得入渗参数(a、b、c和d)。
对于180组膜孔灌土壤湿润体运移过程的拟合,其决定系数R2均大于0.968,说明采用式(6)和式(7)描述湿润半径和湿润深度与时间的关系合适。分析发现12种土壤质地入渗参数b和d的数值变化较小且无明显规律,b介于0.28~0.42之间,d介于0.25~0.41之间,为简化计算,分别取180组b和d的平均数,即b=0.35和d=0.32。将确定的b和d代入式(6)和式(7),原式可进一步变换为
R=at0.35+0.5D
(8)
Z=ct0.32
(9)
利用式(8)和式(9)再次对HYDRUS-2D/3D模拟结果进行拟合,获得a和c。发现R2≥0.912,说明将b和d取平均值来简化模型可行。分析发现不同土壤质地下入渗参数a和c的数值差异很大且规律性不强,采用求平均值法来确定a和c已不现实。进一步分析发现,a和c与稳渗率f0存在良好的幂函数关系(R2≥0.972),如图7所示。
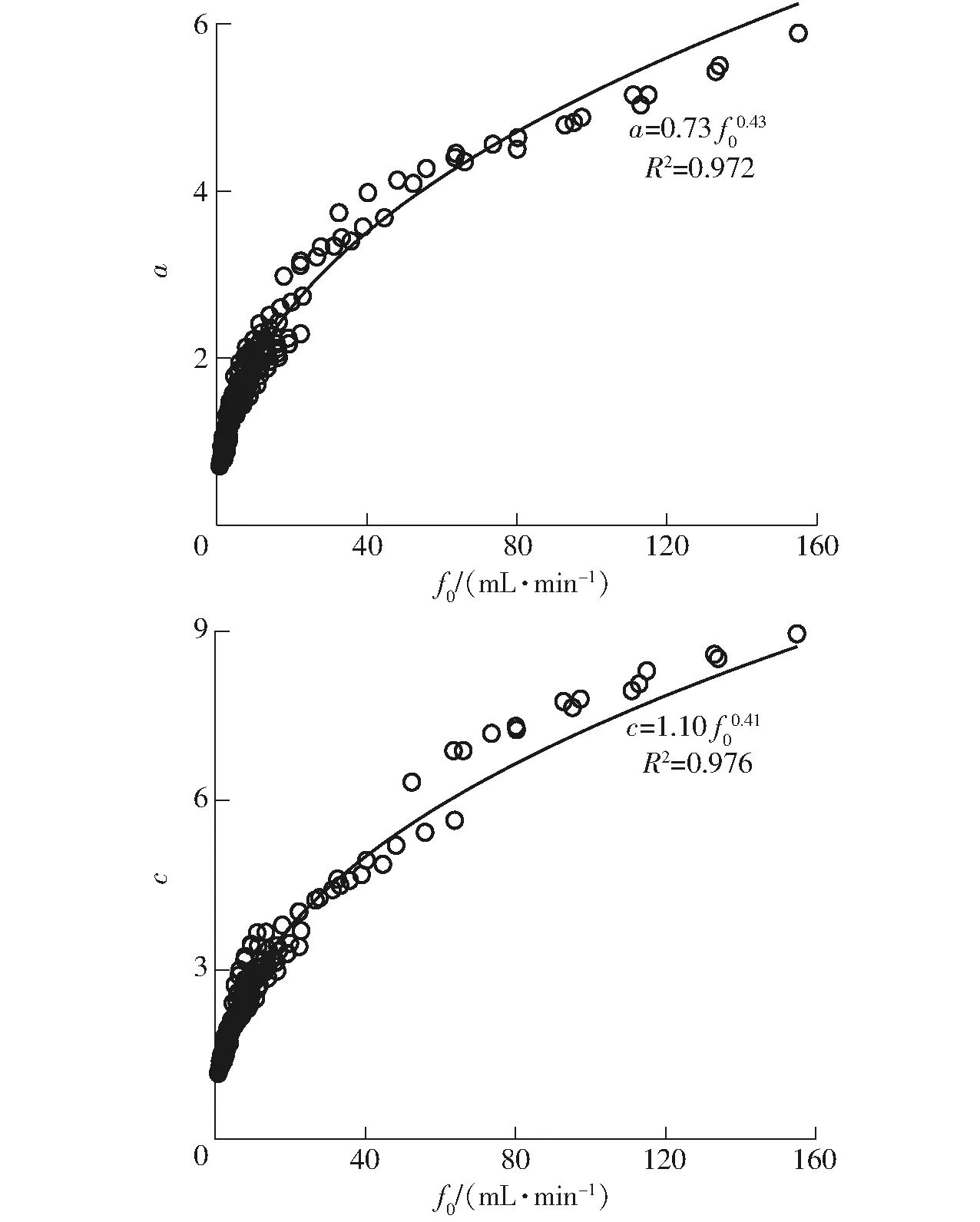
图7 入渗参数a和c与稳渗率f0关系曲线
由图7可知,a和c均随f0的增大而增大,其幂函数关系可表示为
(10)
(11)
将式(10)和式(11)分别代入式(8)和式(9),进一步得到
(12)
式(12)包含了f0这一待定参数,因此,如何确定f0是准确估算湿润半径和湿润深度的关键。通过数值分析稳渗率影响因素可知:相同土壤质地条件下,稳渗率随膜孔直径增大而增大,而随土壤容重增大而减小。选取4种代表性土壤质地,绘制稳渗率与土壤容重和膜孔直径关系曲线,如图8所示(图中砂土f0左轴读数,其他土壤f0右轴读数,下同)。

图8 4种土壤质地下f0与γ和D关系曲线
由图8可知,稳渗率与土壤容重和膜孔直径之间均呈良好的幂函数关系,据此,提出f0与γ和D的函数关系式为
f0=kγuDv
(13)
式中k——待定入渗参数
u、v——拟合参数
对12种土壤质地不同容重和膜孔直径条件下湿润体运移模拟结果进行多元非线性回归,确定u=-6.3和v=1.1。k与土壤质地有关,数值差异较大,无显著性规律,如图9所示。
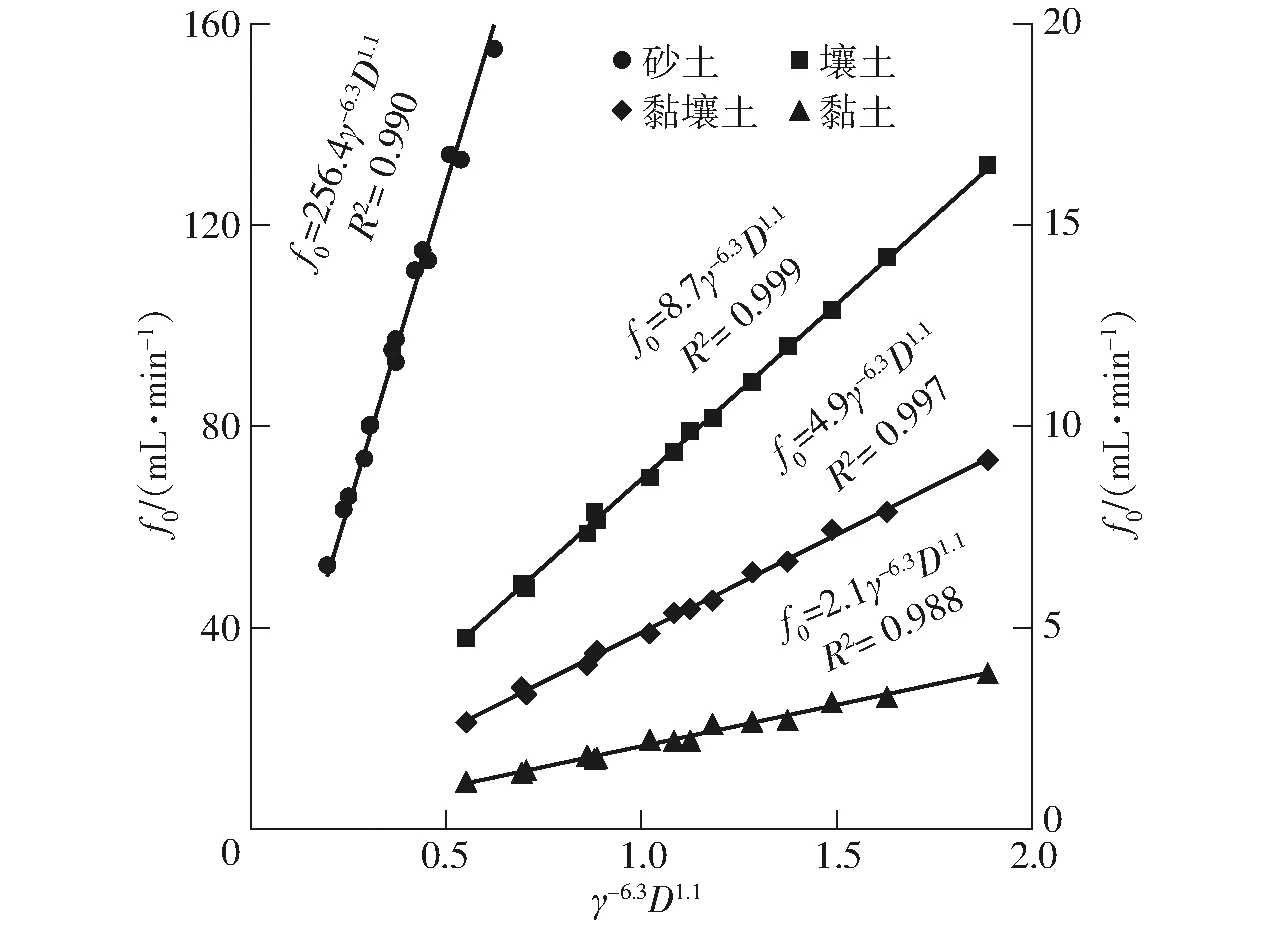
图9 4种土壤质地f0与γ-6.3D1.1关系曲线
由图9可知,对于任一土壤质地,u和v统一取值-6.3和1.1是可靠的(R2≥0.988),而k是与土壤质地相关的待定系数。需要说明的是,土壤质地是根据颗粒机械组成划分,这就导致了农田土壤质地类型保持不变而不同地块差异较大的客观事实,因此,在灌溉系统设计时土壤质地应分情况予以考虑。基于此,将u=-6.3和v=1.1代入式(13),并与式(12)联立,最终可构建出膜孔灌土壤湿润体运移模型
(14)
式(14)仅含一个待定入渗参数k,其值与土壤质地有关,仅需一组室内土箱试验或田间圆筒入渗仪试验获得稳渗率f0,进而反推求得。
2.5 膜孔灌湿润体运移模型评价
为了评价本文所建湿润体运移模型的适用性和可靠性,分别采用文献[5]和文献[7]土箱试验以及圆筒入渗仪田间试验进行验证。
文献[5]采用榆林壤土(γ=1.40 g/cm3),开展膜孔直径为2~6 cm的单点膜孔入渗试验。基于D=6 cm的累积入渗量数据,获取f0=8.89 mL/min,推求k=10.34,进而得到榆林壤土膜孔灌湿润体运移模型
(15)
采用文献[5]中D=3 cm和D=5 cm湿润体半径和深度实测资料对式(15)进行验证,如图10a所示。
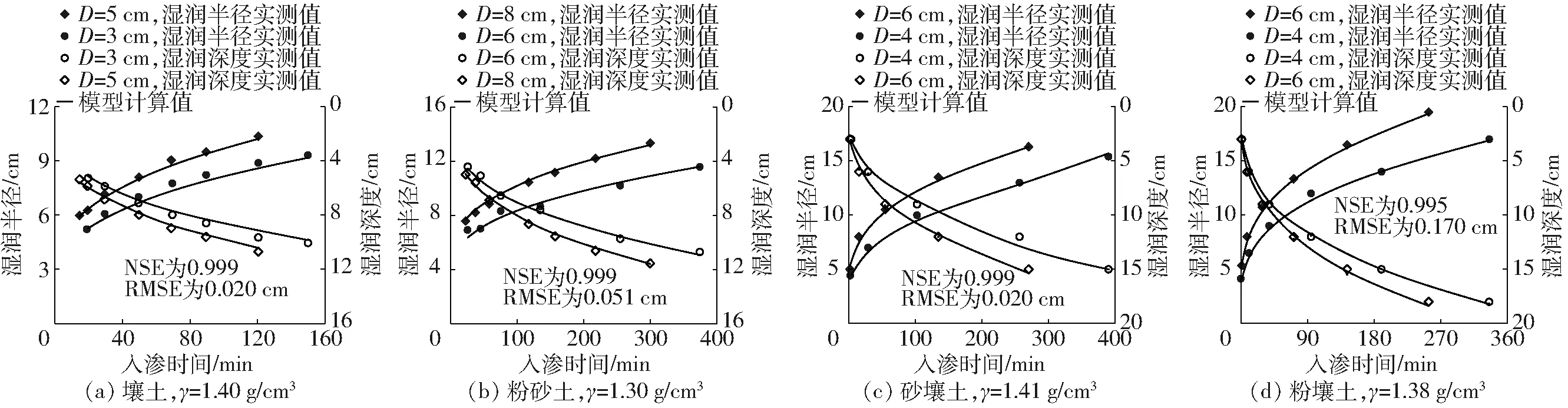
图10 4种土壤膜孔灌土壤湿润体尺寸计算值与实测值对比
文献[7]通过西安粉砂土(γ=1.30 g/cm3)研究了膜孔直径为4~8 cm的浑水膜孔灌入渗特性。本次验证采用D=4 cm的入渗量数据推求f0和k,获取西安粉砂土膜孔灌湿润体运移模型
(16)
利用文献[7]中D=6 cm和D=8 cm的湿润半径和深度实测资料对式(16)进行验证,如图10b所示。
文中模型建立的目的是为了能够对田间膜孔灌土壤湿润体尺寸进行快速的现场评估。因此,模型的可靠性和适用性也理应接受田间现场试验资料的验证。为此,分别选取兰州市魏岭乡狗牙山村和临夏回族自治州西河镇红城寺村基本农田,开展圆筒入渗仪田间试验。为了体现土壤容重的影响,在相近地块选取两处天然容重存在差异的试验点,分别用于参数f0和k的推求和湿润体尺寸的验证。
采用容重为1.33 g/cm3砂壤土的圆筒入渗仪(D=5 cm)水量变化计算f0,确定k=11.01。将k代入式(14),得兰州砂壤土膜孔灌湿润体运移模型
(17)
利用容重为1.41 g/cm3砂壤土的圆筒入渗仪(D为4、6 cm)湿润体运移实测资料对式(17)进行验证,如图10c所示。
采用容重为1.31 g/cm3粉壤土的圆筒入渗仪(D=5 cm)水量变化计算f0,确定k=8.25。将k代入式(14),得临夏粉壤土膜孔灌湿润体运移模型
(18)
利用容重为1.38 g/cm3粉壤土的圆筒入渗仪(D为4、6 cm)湿润体运移实测资料对式(18)进行验证,如图10d所示。
由图10可知,模型计算值与试验实测值在湿润半径和湿润深度上均具有高度的一致性,采用T-Test检验,P>0.05,说明两者之间均无显著性差异。统计指标RMSE接近于0,介于0.020~0.170 cm之间,NSE不小于0.995,趋近于1,表明模型可靠性良好,适用于田间不同质地类型土壤湿润体运移过程的预测。
3 结论
(1)设计了一种能够模拟田间膜孔入渗过程的圆筒入渗仪,其供水单元与渗水单元一体化,结构简单,操作方便,可用于测定田间原状土膜孔灌溉模式下的稳渗率。
(2)相同土壤质地条件下,稳渗率与土壤容重和膜孔直径呈良好的幂函数关系,幂函数指数分别为-6.3和1.1,幂函数系数只需1组圆筒入渗仪田间试验即可推求。
(3)相同土壤质地条件下,湿润半径和湿润深度与稳定入渗率和灌溉时间呈良好的幂函数关系,建立了一种适用于不同土壤质地类型的湿润体运移模型。
(4)田间和室内试验均证实模型可靠性良好和适用性较强,实现了膜孔灌湿润体运移模型在田间的实际应用,方便管理人员进行快速的现场评估。
