多开多备设备组稳态可用度计算方法研究
2023-03-07孙福广王克林胡久韶高振宇
孙福广,王克林,胡久韶,高振宇
(合肥通用机械研究院有限公司,安徽合肥 230031)
0 引言
近年来,RCM(Reliability Centered Maintenance,以可靠性为中心的维修)在各类大型工业领域越来越广泛地得到工业企业的认可与重视,并逐渐在石油化工、电力系统等领域的大型装置中得到更广泛的应用[1]。RCM 技术最核心的作用就是,通过定量RCM 分析为系统设计与维修方案提供提供一定的理论依据,而定量RCM 分析最重要的指标便是其可用度随着时间变换的计算[2]。大型装置系统可用度随时间变换的计算,主要是通过马尔科夫链状态转换矩阵[3-5]进行迭代计算的,一般以1 h为单位,随着使用时间的增加,系统的可用度逐渐趋向于一个定值,即稳态可用度。但是现在,大型机械设备装置已经发展成为一个非常复杂的设备系统,而且机械设备运行时间更长,对设备系统的运行稳定提出了更高的要求。通常情况下,大型设备系统装置的运行时间一般为几万小时或几十万小时起步,因而其装置可用度的计算也带来了几十万次的复杂矩阵转换计算[6]。大多数情况下装置的可用度会随着时间的变化逐渐下降并收敛于一个稳定值,形成平稳分布[7],即稳态可用度。在大型石化、电力等企业,稳态可用度往往对复杂大型装置的设计具有一定参考价值,这就意味着需要计算时间趋向于无穷大时设备状态的分布情况,为了满足精度要求,带来了更为繁重的计算任务。
在实际工程应用当中,用稳态可用度来衡量系统可用度最为常见。但是在计算稳态可用度的过程中,矩阵计算的计算量巨大且计算过程缓慢,有很大不便,导致采用矩阵转换计算设备组稳态可用度的方法在实际工程中遇到了很大瓶颈。尤其是石化、电力企业的大型生产装置,当同时需要计算几十个设备所组成系统的可用度时,无论是空间复杂度过大还是时间复杂度过长,都会导致计算体验较差。此外,过于复杂的计算过程,也为装置设计人员带来了较大的不便[8]。
鉴于传统计算方式的不便,可以推导相关的解析式[6],并依据解析式来计算多开多备设备组的稳态可用度。作为新颖的解决方法,尽管解析式可靠且方便,但因为解析过程中涉及到解微分方程,对于复杂系统而言其推导过程过于复杂,很难得到多开多备复杂系统稳态可用度的解析解。在相关文献中,即使多开多备系统的稳态可用度有解析解,也是假设备用设备的失效率与运行设备失效率相同,而实际上备用设备的失效率与运行设备的失效率完全不同且相差很大,其计算结果也是相差较大,相关的精确度难以得到保证。因此,在计算多开多备设备组的稳态可用度时,需要一个较为贴合实际解析结果的快捷计算方法。可以为多开多备设备组的稳态可用度计算,特别是大型成套装置的稳态可用度计算,提供一个具有参考意义的指标。
为了得到多开多备设备组可用度的快捷计算方法,同时满足工作所需的精度要求,本文首先对一开一备设备组稳态可用度的通用解析解(注意,运行设备与备用设备失效率不同)进行推导。随后依据相关文献[2]与多年的从业经验,将多开多备设备组设备组等效成相似的一开一备设备组,进一步研究其稳态可用度,得到应用于多开多备设备组的稳态可用度计算方法。最后,通过传统矩阵转换的可用度计算结果与该计算方法得到的稳态可用度计算结果进行对比验证,确保了该计算方法在一定精度要求范围内是有效的。
1 一开一备设备组稳态可用度解析式
为了推导出一开一备设备组稳态可用度的解析解,本文设计了一个一开一备设备组模型,根据设备组模型绘制出了模型的状态转换图,接着依据状态转换图得到设备组的状态微分方程,随后借助拉普拉斯变换与拉普拉斯逆变换对状态微分方程进行推导求解,得到了常规一开一备设备组稳态可用度的解析式。
在本文的一开一备设备组中,设备组由两个性能属性相同的设备A 与设备B 组成(在工程应用中通常也是由参数相同的设备组成一开一备或多开多备设备组)。
在设备组中,两个设备的运行失效率与备用失效率分别为λ、λs,失效时,两设备的修复率均为μ。用x(t)表示t 时刻系统的状态,则该一开一备设备组系统共有5 种状态,分别是:
该一开一备设备组的状态转移图如图1 所示,每个状态由3 个方框及字母表示。3 个方框中,第一个方框内标记着运行设备,第二个方框内标记着备用设备,第三个方框内则标记着在维修的设备。字母A 和B 分别代表着设备A 与设备B。只有当两个设备都处于故障时,该一开一备设备组系统故障,即系统处于不稳定状态。因此,当该系统处于状态s0、状态s1、状态s2、状态s3时,系统均处于稳定状态。
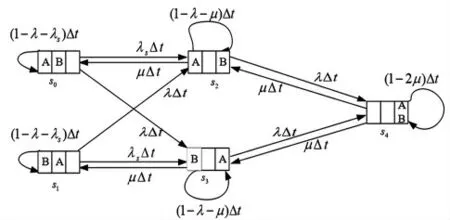
图1 状态转换
根据该一开一备设备组系统的状态转换图,可以得到该一开一备设备组系统的状态微分方程为:
根据式(1)可知,状态s0与s1类似(仅仅是设备A 与设备B所处的状态互换),状态s2与s3也仅仅式设备A 与设备B 的状态互换,因此本文定义状态0 为状态s0与s1二者的状态,状态1为状态s0与s1二者的状态,状态2 为状态s4,该得到该系统新的状态。结合前文,该系统的稳定状态为状态1 和状态2。该系统的状态微分方程为:
根据该系统新的状态微分方程,对方程组进行拉普拉斯变换。结合该系统的初始条件P0(0)=1,Pi(0)=0,i=1,2,对式(2)进行求解,可以得到求解结果:
同时,考虑到在稳定状态下,系统各状态的概率不随时间变化,为恒定常数,因此系统的各个状态满足满足t→∞:Pj(t)→Pj(j=0,1,2)。根据该条件,得到该方程组的解析解为:
2 多开多备设备组稳态可用度快捷计算方法
为了得到多开多备设备组稳态可用度的快捷计算方法,本文首先查阅了文献[2]、文献[6],得到串联系统与并联系统的等效失效率、修复率,然后将多开多备设备组等效为一开一备设备组,根据企业对系统的不同要求、标准,将多开多备设备组分为装置停车、降负荷两种情况,并结合工程应用实践得到了多开多备设备组在装置停车、降负荷两种情况下的等效运行失效率、等效备用失效率以及等效修复率等相关等效参数。
在处理多开多备设备组系统的过程中,可以根据该系统内的各个设备的状态(工作状态/备用状态)将复杂的多开多备设备组分为工作子系统与备用子系统。在工作子系统与备用子系统内部继续进行工作子系统、备用子系统的进一步划分,直到划分到具体的单个设备。在划分过程中,分别根据式(9)与式(11)得到不同设备以及子系统所组成系统的失效率与修复率。随后再进一步采用由两台设备所组成的并联可用度解析式进行下一步的计算。根据文献[2]可以得到串联子系统失效率λs为:
其中,λi(i=1,2,…n)为设备失效率。
在由失效率分别为λ1与λ2所组成的两设备并联子系统中,根据文献[6]可得到该并联系统的可用度解析式为:
式中各参数表达含义为:
查阅文献[2]可以得到关于并联系统的失效率与修复率的解析式,根据该式进一步进行推导计算,可以得到并联系统的等效失效率λp:
2.1 导致装置停车情况的设备组可用度
在大型装置中,同一多开多备设备组系统的所有设备参数相同。每个设备的工作失效率、备用失效率与修复率分别为λ、λst和μ。与此同时,在实际工程中多开多备设备组的所有设备在物理上是并联的,当所有的并联设备全部停止工作时,设备组所有设备会进入维修状态,从而导致整个装置停车。在这种情况下,多开多备设备组的所有运行设备在逻辑上也是并联的。与运行装备一样,备用设备在物理上、逻辑上也都是并联的。另外,在大型企业中,物资、人力资源较为充沛,因此对于任意子系统的修复率视作恒常量μ。
基于以上思路,本文分别给出了常见泵组一开一备、两开一备、三开一备、四开一备以及五开两备泵组中λ1,λ2,μ1μ2(一开一备设备组等效参数)的计算公式(表1)。
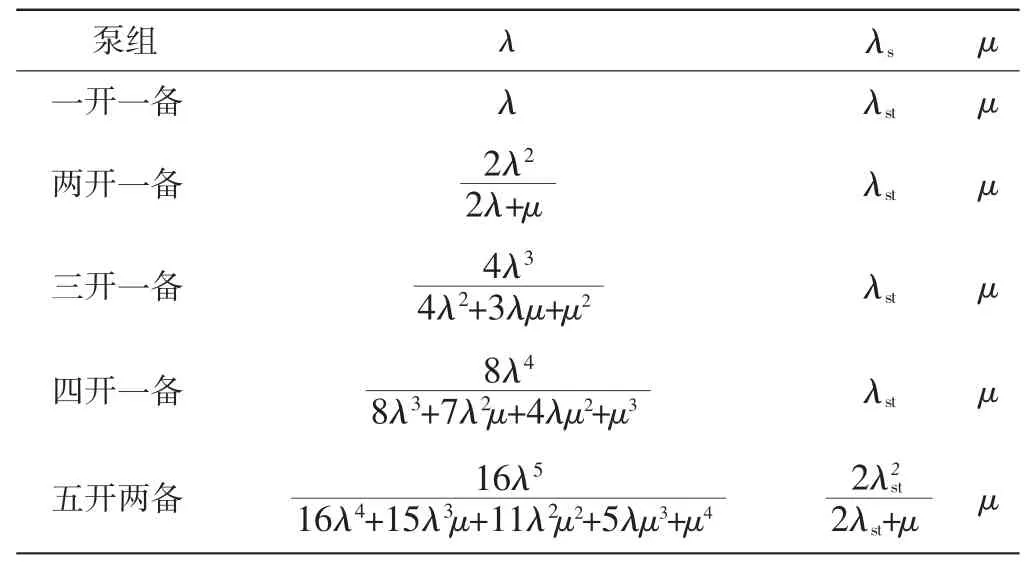
表1 多开多备停车情况的相关参数
2.2 导致装置降负荷情况的设备组可用度
在与上一节条件相同的多开多备设备组系统中,虽然多开多备设备组在物理上是并联的,但是在实际工程的过程中,当运行设备的数量减少同时备用设备故障时,由于设备组的运行设备数量减少,装置会进入降负荷工作的状态,故而各设备之间在逻辑上属于串联状态。图2 为两开一备该种状态下的状态转换图。
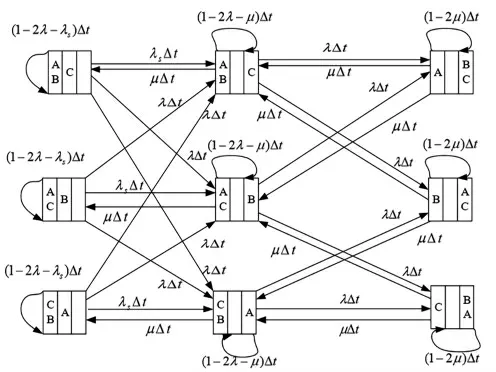
图2 两开一备降负荷情况状态转换
在两开一备设备组中,当损坏设备达到两台之后,系统降量工作,认为系统处于不可用状态。根据两开一备的状态转换图,可以得到类似一开一备的状态微分方程:
本文同样对三开一备、四开一备等设备组进行了研究,由于其状态转换图与一开一备、两开一备十分接近且过于复杂,本文只给出其对应的状态微分方程。
(1)三开一备的状态微分方程:
(2)四开一备的状态微分方程:
对比式(2)、式(12)、式(13)与式(14),对多开一备设备组印证了前文中所提到的工作设备在逻辑上是串联的。
同样,本文对多开多备设备组进行了研究,给出了一开两备、五开两备设备组的状态微分方程。
(3)一开两备的状态微分方程:
(4)五开两备的状态微分方程:
对比式(15)与式(16),对多开多备设备组同样印证了前文中提到的“工作设备在逻辑上是串联的,备台设备在物理上、逻辑上都是并联的”。根据以上分析,本文分别给出了多开多备泵组中λ,λs,μ1μ2(一开一备设备组系统等效参数)的计算公式。
3 实例计算
假设在多开多备离心泵组中,单台泵的运行失效率为λ=5×10-5失效/h,备用失效率为λst=5×10-7失效/h,修复率恒定为μ=0.008 修复/h。离心泵组常用的组合方式有一开一备、两开一备、三开一备、四开一备、五开两备,通过等效一开一备的处理方式来计算泵组的不可用度。上述泵组的一开一备等效参数及不可用度见表3。
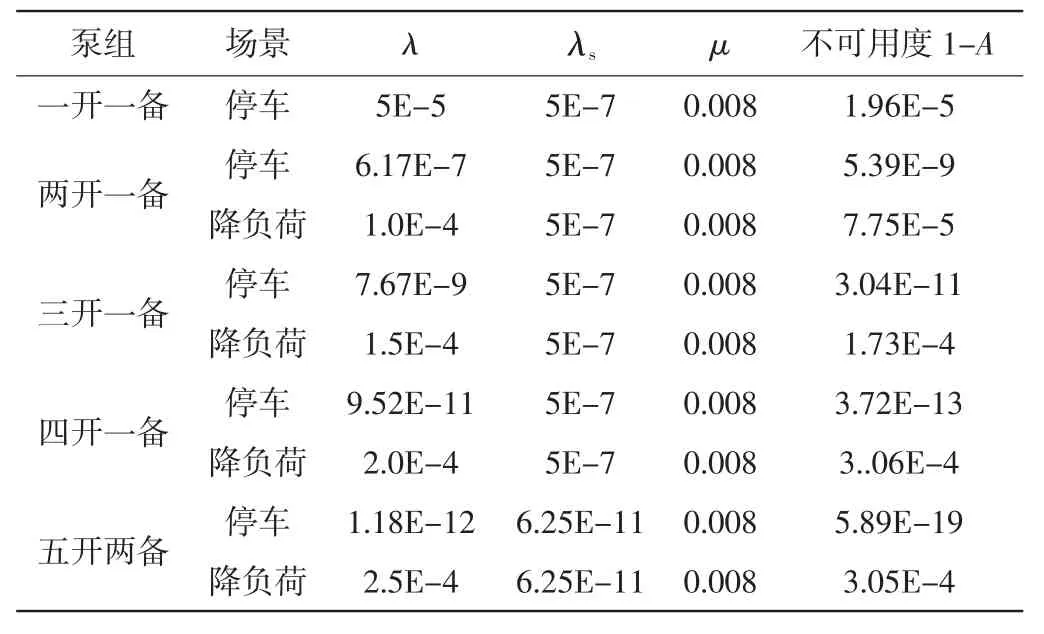
表3 多开多备泵组不可用度计算表
由表2 和表3 可知,多开多备导致装置停车的事件概率非常低。工程上,多开多备泵组主要问题是导致装置降负荷运行。从降负荷概率来看,多开一备的可用度比一开一备的会更低,这也与实际工程经验相符。

表2 多开多备降负荷情况的相关参数
4 结论
本文从一开一备设备组可修系统的状态转换方程入手,推导工作失效率与备用失效率不同的一开一备设备组稳态不可用度计算的解析式。并根据一开一备设备组的可用度表达式推导出多开多备设备组可用度的等效表达式,通过将多开多备设备组等效为一开一备设备组的处理方式解决了多开多备设备组可修系统稳态可用度的复杂计算问题,在满足一定精度条件的前提下大大提高稳态可用度的计算效率。实践证明,该处理方式能够满足实际工程需要,尤其是适用于大批量设备组的可用度计算,这对RCM 技术在我国过程成套装置的推广应用具有重要意义。
