压力补偿滴头流动阻力分析与流量预测研究

牛文全 孙 丹 甘海成 董爱红 邬梦龙 吕 畅

(1.西北农林科技大学旱区农业水土工程教育部重点实验室， 陕西杨凌 712100；2.中国科学院水利部水土保持研究所， 陕西杨凌 712100；3.西北农林科技大学水利与建筑工程学院， 陕西杨凌 712100)

0 引言

滴灌技术能够有效实现节水增产、调控和管理农田生态环境以及水肥药精量控制，是节水灌溉的主要方式之一[1]。压力补偿滴头作为滴灌系统的核心部件之一，其毛管铺设距离较大，适应的地形更广，灌水均匀且抗堵性能好[2]。目前我国部分灌溉企业自主研发了一些压力补偿滴头产品，但大多以管上式压力补偿滴头为主，针对不同结构类型的压力补偿滴头系统设计方法还未见报道。为探索压力补偿滴头的设计方法，大量专家学者[3-6]通过开展水力性能试验确立了压力补偿滴头结构和材料参数与水力性能的关系。然而室内试验周期长、成本高，很难直接观测压力补偿滴头的工作机制[7]。近年来，随着计算流体力学的发展，利用数值模拟方法可视化研究滴头内流场，提高了滴头的研发效率[8-9]。

压力补偿滴头主要由消能迷宫流道、压力补偿腔和弹性片组成。弹性片在水流作用下会发生变形和非线性运动，进而改变流体的流动，因此对压力补偿滴头的数值模拟需要进行流固耦合[10]。武永安[11]采用ANSYS软件对压力补偿滴头内部流场进行了稳态数值计算，但未考虑弹性片变形对流体区域的影响。周兴等[12]研究认为0～40 kPa范围内压力补偿滴头的流固耦合数值计算结果与实际测试结果接近。楚华丽等[13]基于流固耦合方法并结合可视化试验探究了0～90 kPa范围内弹性片的变形和流场特性，可视化试验所得不同截面处的速度分布、漩涡位置和数量与流固耦合计算结果吻合。但目前只在较小的压力范围内，采用流固耦合方法模拟了压力补偿滴头的工作过程，当弹性片接触凸台后，即较高工作压力下压力补偿滴头的数值模拟研究还较少。压力补偿滴头结构复杂，其迷宫流道、弹性片与水流之间的相互作用会产生一定的流动阻力，导致水流能耗增加，影响滴头流量。弹性片作为主要调节元件，其变形特性极大地影响着滴头性能，因此研究并探明弹性片变形引起流动限制的机理对改进滴头设计极为重要[14]。SHAMSHERY等[15]根据TAYLOR等[16]建立的压力补偿滴头数学模型，分析了滴头内水流能耗随工作压力的变化情况，并对结构和材料参数进行研究，然而理论分析过程中抽象和简化了弹性片的受力与变形，理论解与实际弹性片的非线性变形有较大差异。因此，为了制定合理的压力补偿滴头设计方法，亟待开展基于流固耦合模拟计算方法，研究全压力范围内压力补偿滴头的弹性片变形特性及流动阻力变化特征。

为此，本文采用基于RANS模型的瞬态和稳态流固耦合数值计算方法，分别研究弹性片接触凸台前和接触凸台后压力补偿滴头流动阻力的动态变化，分析不同工作压力下弹性片变形-流动阻力-流量间的关系。根据弹性片变形特性和流动阻力变化特征确定影响滴头补偿性能的主要因素，以期为压力补偿滴头的优化设计提供参考。

1 材料与方法

1.1 试验材料

本研究选择的压力补偿圆柱滴头结构如图1所示。图中L表示压力补偿腔长度，W表示压力补偿腔宽度，w表示副流道宽度。压力补偿滴头由外壳、弹性片和滴头主体构成，滴头主体上有迷宫流道、压力补偿腔、凸台、副流道和出水口等，迷宫流道结构和压力补偿腔结构如图2所示。图中a表示迷宫流道深度，b表示迷宫流道宽度，θ表示齿夹角，H表示压力补偿腔高度，h表示副流道深度，m表示凸台高度，d1表示凸台直径，d2表示出水口直径，d3表示压力补偿腔进水口直径。弹性片为硅橡胶材质，长度、宽度和厚度分别为8.6、5.9、0.78 mm，邵尔硬度为58 HA。滴头的结构参数如表1所示，n表示迷宫流道单元个数。

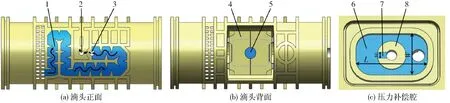
图1 压力补偿滴头三维结构示意图Fig.1 3D schematics of pressure compensating emitter1.迷宫流道 2.出水口 3.压力补偿腔进水口 4.压盖 5.弹性片 6.压力补偿腔 7.副流道 8.凸台

表1 滴头尺寸Tab.1 Dimensions of emitter

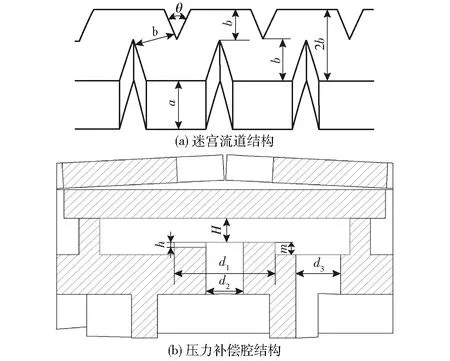
图2 压力补偿滴头二维结构示意图Fig.2 2D schematics of pressure compensating emitter

1.2 数值模拟方法

压力补偿滴头的数值分析模型包括流体域和可变形固体结构。在不同的求解器中分别求解流体控制方程和固体控制方程，通过满足流固交界面处的边界条件耦合在一起[17]，以实现流体域和固体域计算结果的互相交换和传递。

1.2.1流体分析

采用Fluent 6.3软件模拟水在流道中的流动特性。由于流体域形状不规则，采用非结构的四面体单元对其进行网格划分。构建了6套网格，网格最大尺寸分别为0.100、0.125、0.150、0.175、0.200、0.300 mm，对应的网格单元数量分别为926 000、554 000、351 000、239 000、173 000、75 000，对流体网格进行独立性检验。在入口位置施加50 kPa进行流体区域CFD计算，统计出口流量随网格数变化关系，如图3所示。选用最大尺寸为0.15 mm的网格对流体域进行划分，网格模型如图4所示，总单元数为351 366个。选择SST(Shear stress transfer)k-ω湍流模型进行求解，求解方程包含质量守恒方程、动量守恒方程以及雷诺应力输运方程等。滴头内的流体为常温水，属于不可压缩粘性流体，密度ρ为常数，由于不考虑热交换，流体的控制方程为[18-19]

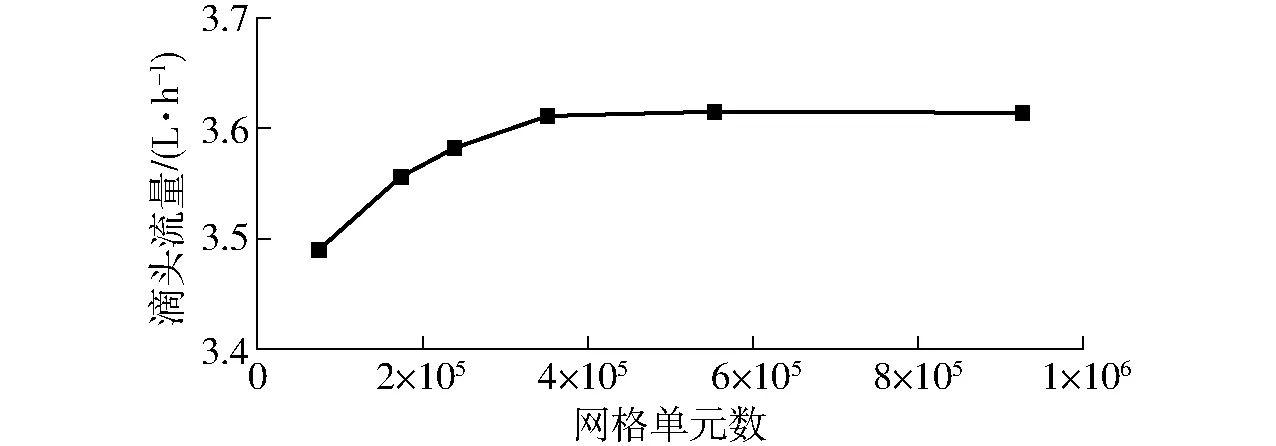
图3 滴头流量随网格单元数的变化曲线Fig.3 Relationship between flow rate and number of grid cells

图4 流体网格模型Fig.4 Fluid mesh model1.进口 2.流固耦合面 3.出口

质量守恒方程

(1)

动量守恒方程

(2)

(3)

(4)

输运方程

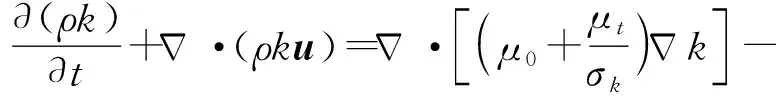
(5)

(6)

式中P——流体微元体上的压力，Pa

k——湍流动能

μt——湍流粘度，Pa·s

ω——湍动能耗散率

u——速度矢量，m/s

μ——流体粘度，Pa·s

μ0——层流粘度，Pa·s

u、v、w——速度分量，m/s

β*、σk、β、σω、σω2——常数系数

F1——开关函数，对壁面湍流，F1=1；对自由剪切湍流，F1=0

Fx、Fy、Fz——流体微元体上的体力，体力只有重力，则Fx=0，Fy=0，Fz=-ρg

数值计算时将流体入口设置为压力入口，入口压力采用逐步增量加载方式，加载量由时间步长的函数和步数综合控制；流体出口设置为大气压；流体与弹性片的接触面设为流固耦合面，其余流体边界均为壁面。瞬态流固耦合分析中，弹性片的变形导致流体计算区域几何形状发生改变，设置动态网格，采用扩散光顺与局部重构结合的动网格方法，增大网格更新频率、减小网格更新的最大歪斜度来实现计算区域的网格更新。采用动态网格自适应方法对流场压力、速度梯度较大的区域进行网格细化。由于Fluent本身功能有限，不能在计算过程中改变边界状况，故在流固耦合面与流体壁面之间保留了一层最小尺度的网格[20]，以保证流体域网格变形过程中数值正常传递。采用SIMPLEC(Semi-implicit method for pressure-linked equations consistent)算法求解流体方程。

1.2.2结构分析

弹性片为硅橡胶材料，本文选用Neo-Hookean M-R橡胶材料模型，该材料模型具有恒定的剪切模量，与单轴拉伸应变高达40%和单轴剪切应变高达90%的实验数据具有良好的相关性[21]。其第1系数C1等于剪切模量的一半，第2系数C2等于零[22]，弹性模量与材料系数的关系为

E=6(C1+C2)

(7)

弹性模量与硬度的关系为

(8)

式中E——弹性片弹性模量，Pa

HA——弹性片硬度，HA

在瞬态结构分析软件中计算弹性片的变形。采用四面体单元对弹性片进行网格划分，网格尺寸取0.3 mm。对流固耦合面进行面网格划分，网格尺寸取0.15 mm，与流体域的网格尺寸一致，以保证流固交界面数据传输的精确性。网格模型如图5所示，总单元数为25 108个。弹性片运动方程为

图5 弹性片网格模型Fig.5 Elastic diaphragm mesh model1.压力加载面(弹性片上表面) 2.固定约束面(弹性片下表面) 3.流固耦合面

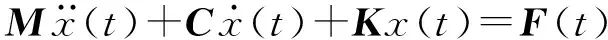
(9)

式中M、C、K——质量、阻尼系数、刚度矩阵

F(t)——流体作用在固体上的外力

滴灌管中的水流经滴头时，水流压力作用在弹性片上表面，这一部分水流会顺管道流走，流体域中并未建模。结构分析中在弹性片上表面设置压力荷载，压力与流体入口压力相同，采用逐步增量的方式加载。在弹性片下表面边缘设置固定约束；弹性片下表面与压力补偿腔流体的接触面设为流固耦合面。对于稳态流固耦合分析，在静态结构分析软件中建立弹性片与凸台相互作用的力学模型，两者之间的接触类型选用摩擦接触，摩擦因数取0.2[14]。弹性片划分方式与瞬态流固耦合相同。

1.2.3流固耦合分析

在瞬态流固耦合计算中，采用系统耦合软件创建流体区域和结构区域的数据传输，力和位移的收敛精度为0.01。在系统耦合中设置重新启动数据，启动间隔为需要备份点的频率。流固交界面作为压力与位移数据的传输面，应满足力平衡和位移协调条件：

动力学条件

n·τf=n·τs(X∈Si;t∈[0,T] )

(10)

运动学条件

df=ds(X∈Si;t∈[0,T])

(11)

式中n——单位法向量

τf、τs——流体和结构应力，Pa

X——几何点坐标

Si——流固耦合面t——时间，s

T——瞬态计算总时间，s

df、ds——流体和固体位移，m

稳态流固耦合计算的是弹性片接触凸台后的变形，此时弹性片变形由其上下表面的压差和凸台的接触力综合决定[23]。首先假定作用在弹性片上的压力荷载为Ps，在静态结构中计算弹性片的变形；根据变形结果建立流体分析模型，采用Fluent模拟流场，确定流体进口面与弹性片下流固耦合面之间的压差Pf；若Ps≈Pf，说明计算结果与实际工况相符，若不相等，则需重新确定Ps，循环上述过程，直至满足条件。稳态流固耦合求解流程如图6所示。

图6 稳态流固耦合计算流程图Fig.6 Flow chart of calculation process of steady fluid-structure interaction simulation

1.3 流动阻力计算方法

压力补偿滴头的横截面如图7a所示，流体以压力P1流入滴头，然后流经迷宫流道进入弹性片下方的矩形压力补偿腔，这一流动过程产生一定的压力损失，导致补偿腔内的压力降为P2。腔内流体直接或经过凸台上的副流道从出水口流到大气中，大气压用Pa(0 Pa)表示。滴头流动阻力参数K可以表示为流量和压力的函数[24]，即

P1-Pa=Q2K

(12)

式中Q——流量，L/h

监测不同进口压力下迷宫流道末端的压力和流量，迷宫流道流动阻力系数K1可以表示为流量和压降的函数，即

(13)

当进口压力较小时，弹性片在压力补偿腔中发生变形，如图7b所示。由于未接触凸台，水流可以从弹性片下表面流出出口，压力补偿腔流动阻力系数K2可以表示为

(14)

当进口压力较大时，弹性片变形到接触凸台并覆盖出水口，此时第2种流动状态开始，如图7c所示。所有水流均通过副流道流出，随着进口压力的增加，弹性片剪切进副流道中的体积增加，副流道流动阻力系数K3的计算公式为

图7 滴头横截面示意图Fig.7 Cross sections of emitter1.弹性片 2.副流道 3.凸台 4.压力补偿腔

(15)

1.4 水力试验方法

根据文献[25-26]搭建滴头压力流量关系测试平台如图8所示。共布置25个滴头，滴头间距为50 cm。试验进水口压力设置为10、20、30、40、50、69、100、150、200、250、300 kPa，共11个压力水平。试验开始前将压力调至10 kPa并保持3 min，然后调至300 kPa，保持3 min，循环3次后将压力调至 100 kPa，保持42 min，整个调节过程60 min。测量前调整压力表读数至稳定，保持3 min后将量筒放置滴头下方开始测试。

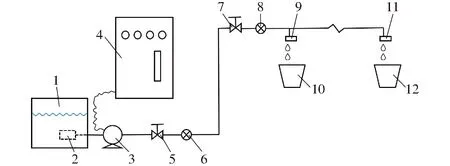
图8 水力性能试验装置示意图Fig.8 Schematic of hydraulic performance test device1.水箱 2.过滤器 3.水泵 4.变频稳压器 5、7调压阀 6、8.压力表 9、11.滴头 10、12.量水筒

测量时间为5 min，在每个压力下，对滴头进行3次测量,流量取3次的平均值。滴头流量的计算公式为

(16)

(17)

Qi——每次测得的流量，L/h

t1——测量时间，min

m0——量筒质量，g

mi——时间t1内水和量筒总质量，g

2 结果与分析

2.1 模型验证

滴头流量模拟结果与实测结果如图9所示。在不同压力范围内，模拟值与实测值的差异略有不同。弹性片接触凸台前，模拟值高于实测值。这是由于弹性片实际变形时，会与滴头壳体产生微小的接触分离[27]，导致作用在弹性片上的约束力减小，实际变形量增大，补偿腔内的过流面积由此减小，实测流量较小。弹性片接触凸台后，模拟值低于实测值。为保证收敛速度，模拟计算时容许弹性片与凸台间存在穿透容差，穿透量的设置导致弹性片剪切进副流道中的体积增大，副流道中过流面积随之减小，模拟流量较小。当进口压力大于200 kPa时，弹性片的变形增量极小，流量的相对误差最小。流量模拟值与实测值间的最大误差为25.4%，主要发生在弹性片接触凸台前的快速变形阶段。由于压力补偿滴头的流量与弹性片变形量之间有精确的关系[12]，相比于弹性片的微小变形，快速变形导致弹性片模拟工况与实际工况间的差异增大，因此该阶段流量的相对误差最大。进口压力0～300 kPa范围内模拟值与实测值的平均误差为12.32%，说明数值模拟方法能够较为准确地预测压力补偿滴头的流量。

图9 模拟与实测流量对比Fig.9 Comparison of flow rates between simulated and measured values

压力-流量关系曲线以50 kPa为拐点，呈现快速上升和相对稳定两个阶段。弹性片变形至接近凸台时，由于压差变化，会处于接触凸台然后与之分离的周期性振动状态[13,27]，这会引起压力补偿滴头的流量出现波动。本研究所选用的弹性片硬度较大(硬度为58 HA)，弹性片的硬度越大，对压力差的变化越不敏感[28]，故当弹性片变形至接近凸台时(50 kPa)，压力-流量曲线相对稳定。此外，数值计算时，弹性片上的压力连续加载且荷载增量极小，弹性片的变形过程稳定，压力-流量曲线先上升后平稳，这与前人研究一致[12,23]。

2.2 弹性片变形特性

图10为弹性片接触凸台前(图10a)、弹性片接触凸台时(图10b)和弹性片变形进入副流道后(图10c)的变形云图。弹性片的最大形变发生在中心部位，最大变形量随工作压力的增加而增大。当进口压力为69 kPa时，弹性片变形量约为0.66 mm，占0～300 kPa总变形量的92.1%。当进口压力超过69 kPa时，弹性片接触凸台，其变形受到接触力限制。300 kPa时，弹性片底部与凸台完全贴合，部分剪切进副流道中。

图10 不同进口压力下弹性片的变形量Fig.10 Deformation of elastic diaphragm at different pressures

弹性片变形量与进口压力关系曲线如图11所示。弹性片在压力0～300 kPa范围内的变形过程可分为3个阶段：0～40 kPa区间，弹性片随压力的增加发生快速变形；40～69 kPa区间，随着压力的增加，弹性片的变形增量减小，发生缓慢变形；69 kPa之后，弹性片的变形增量极小，在副流道中发生长期微小变形。

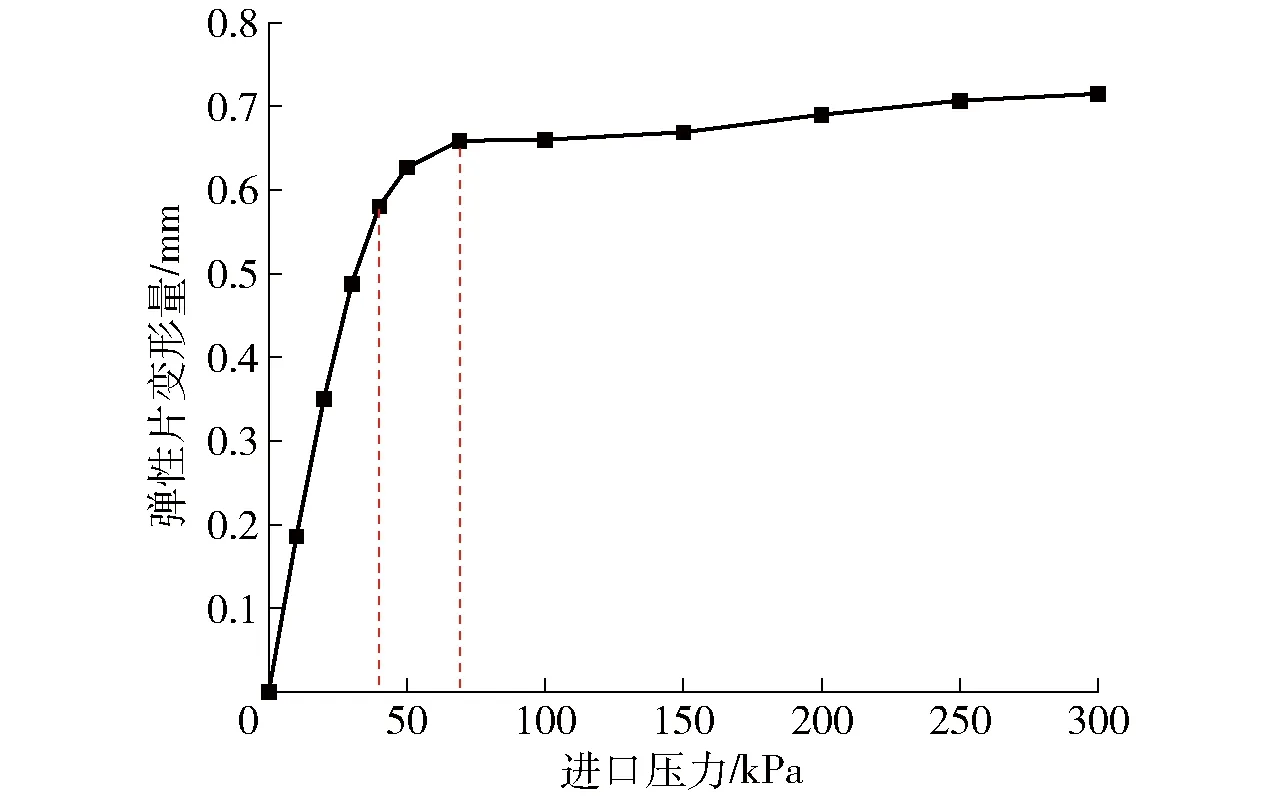
图11 弹性片变形量与进口压力关系曲线Fig.11 Relationship between deformation of elastic diaphragm and inlet pressure

2.3 流体出流特性

弹性片的变形结果决定了压力补偿滴头的出流特性和流场分布情况。不同进口压力下流场截面压力、速度分布如图12所示。压力补偿滴头的出流截面由压力补偿腔径向截面和副流道横截面两部分组成。当进口压力为20 kPa时，压力能主要消耗于迷宫流道，弹性片由于压差作用发生明显变形，压力补偿腔中的径向出流截面减小(图12a)。迷宫流道的转角和补偿腔出口流速最大，补偿腔内的流速稳定；当进口压力达到69 kPa时，迷宫流道处的压力损失增加，弹性片上下表面压差增大，弹性片变形至接近凸台几乎覆盖出水口(图12b)，大部分水从副流道流出滴头，补偿腔中过流面积极小。最大流速位于副流道处和弹性片下表面的最小过流断面处，补偿腔内存在大面积的低速区，但补偿腔出口附近的流速梯度较大。当进口压力为300 kPa时，迷宫流道处压力损失增量减小，此时弹性片上下表面的压差增量远小于进口压力的增量，弹性片在副流道中发生微小变形，副流道中的过流面积减小，副流道中的高速水流区域减小、水流速度增加(图12c)。

图12 不同进口压力下流场的压力、速度分布Fig.12 Pressure and velocity distribution of flow filed at different pressures

2.4 迷宫流道、压力补偿腔和副流道压力损失

弹性片的变形改变了压力补偿滴头的出流截面，导致压力补偿腔和副流道处的过流面积减小、压力损失增加，流场各位置的压力损失特征发生明显变化。不同进口压力下流场各位置压力损失占比如图13所示。弹性片接触凸台前，压力损失主要发生在迷宫流道部位。压力补偿滴头的出流截面包括补偿腔径向截面和副流道横截面两部分。随着进口压力的增加，补偿腔出流截面减小、压力损失增加。当进口压力由20 kPa增加到69 kPa时，迷宫流道压力损失占比由90%减小为59.4%，补偿腔压力损失占比由10%增长为40.6%。弹性片接触凸台后，压力补偿滴头的出流截面仅剩副流道横截面，且随着进口压力的增加，副流道出流截面减小、压力损失增加。当进口压力达到300 kPa时，副流道处压力损失占总压力损失的81.7%。

图13 不同进口压力下流场各位置压力损失占比Fig.13 Proportion of pressure loss at different positions of flow field at different pressures

2.5 迷宫流道、压力补偿腔和副流道流动阻力

工作压力为20 kPa(雷诺数Re>500)时迷宫流道流速矢量分布如图14a所示。压力水流与流道锯齿之间发生相互作用，导致流道中产生漩涡并形成湍流。迷宫流道流动阻力系数随雷诺数变化关系如图14b所示。阻力系数K1的平均值和标准差分别为2 987、52 Pa·h2/L2，与平均值相比，K1的标准差非常小，只占平均值的1.74%，且K1在雷诺数大于500之后的变化极小。因此，当流道中的水流发展为湍流之后，迷宫流道流动阻力与雷诺数无关，可视为一个定值。

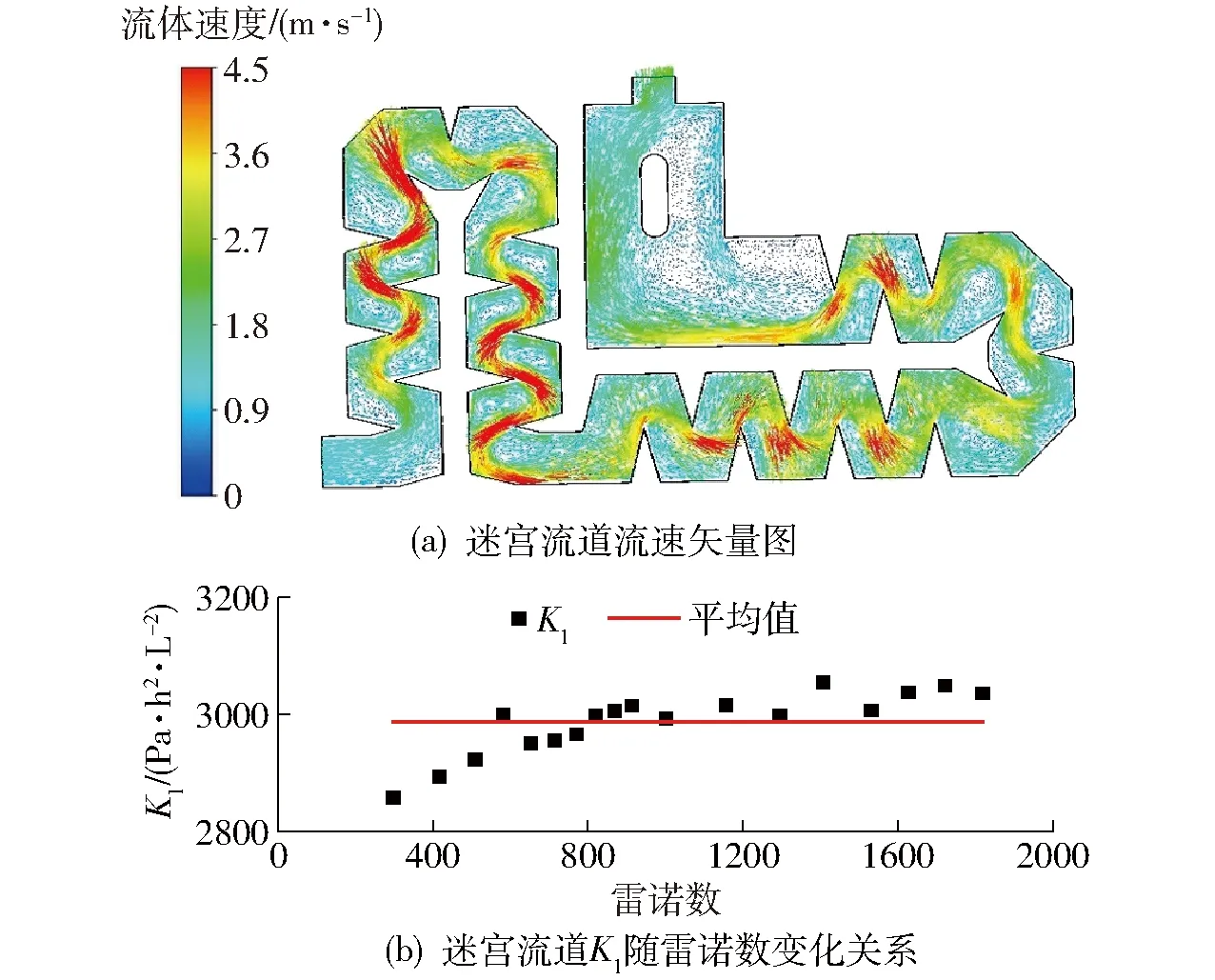
图14 迷宫流道水力特性Fig.14 Hydraulic characteristics of labyrinth channel

压力补偿滴头流动阻力系数随进口压力的变化曲线如图15所示。压力0～40 kPa范围内，弹性片发生变形未接触凸台，总流动阻力系数主要取决于迷宫流道的流动阻力系数K1，压力补偿腔流动阻力系数K2增量极小。由于流动阻力较小，流量随压力的增加快速增长；压力40～69 kPa范围内，弹性片变形到接近凸台即将覆盖出水口，补偿腔流动阻力系数K2的增量随压力的增加逐渐增大，流量随压力的增加缓慢增长；69 kPa之后，弹性片受到凸台接触力的限制并开始剪切进入副流道，副流道流动阻力系数K3随压力增加呈线性增长趋势，滴头流量随压力增加趋于恒定。压力补偿腔流动阻力系数在工作压力为0～40 kPa和40～69 kPa范围内的增量分别为535 Pa·h2/L2和1 573 Pa·h2/L2，副流道流动阻力系数在工作压力为69～300 kPa范围内的增量为15 763 Pa·h2/L2。补偿腔和副流道处的流动阻力分别在进口压力为69 kPa和300 kPa时达到最大。与迷宫流道所产生的固定流动阻力相比，补偿腔最大流动阻力小于迷宫流道流动阻力，副流道最大流动阻力是迷宫流道流动阻力的5.3倍。

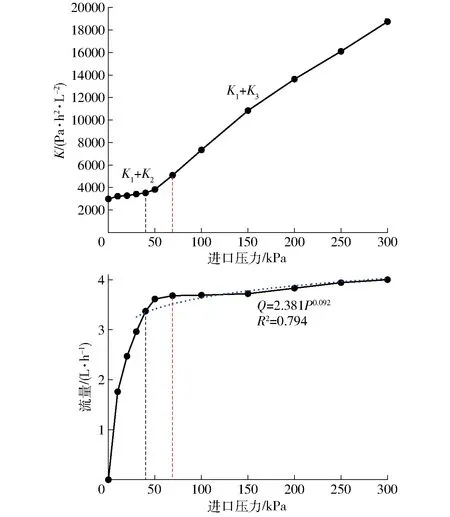
图15 流动阻力系数、流量与进口压力关系曲线Fig.15 Relationship of flow resistence and flow rate with inlet pressure respectively

3 讨论

本研究采用基于RANS模型的流固耦合计算方法，对压力补偿滴头全压力范围内的数值模拟进行了探索。采用有限体积法对计算区域进行离散，同时考虑了流体网格尺寸对计算结果的影响，保证了计算精度及适当的计算时间。弹性片随工作压力的增加发生变形，造成流体网格压缩破坏，降低了网格质量[23]。为确保计算顺利进行，启用动网格设置对变形后的流体网格进行重构，采用逐步加载入口压力的方式并结合重启动分析方法完成压力补偿滴头的瞬态流固耦合数值计算。弹性片接触凸台后，两种结构之间的接触使流体网格发生断裂，流固耦合数值无法正常传递，瞬态数值计算出现困难。因此，建立了弹性片与凸台相互作用的力学模型，通过满足流固交界面处的收敛条件完成压力补偿滴头的稳态流固耦合数值计算。通过模拟和实测数据对比发现，模拟值与实测值随压力的变化趋势吻合较好，表明该耦合方法有效、合理。

压力损失通常取决于雷诺数和流动路径的几何形状[29-31]，流动阻力是产生压力损失的直接原因。迷宫流道属于微流道，存在微尺度效应[31]，其中水流的湍流起始点较低，临界雷诺数在250～500之间[33-34]。当工作压力为20 kPa时，迷宫流道的雷诺数大于500，故在所研究的大部分压力范围内，通过迷宫流道的流动为湍流。流动阻力系数K1不随雷诺数发生明显变化，因此迷宫流道流动阻力与雷诺数无关，其大小仅取决于流道的几何形状；弹性片的变形改变了压力补偿腔和副流道出流截面的几何形状，弹性片的变形程度越大，流体的出流截面愈小。当弹性片接触凸台后，出流截面仅剩副流道横截面，随着压力升高，弹性片在副流道中发生微小变形，副流道处过流面积减小、有效过流长度增加[15]，副流道流动阻力随压力升高而线性增长。因此压力补偿腔和副流道流动阻力是可变的，其大小取决于弹性片的变形程度，弹性片变形进补偿腔和副流道中的体积越大，滴头产生的流动阻力愈大。

弹性片覆盖于压力补偿腔上部，滴头工作时，弹性片的受力可视为简支的矩形膜[14]，中心部位的变形量最大。弹性片的变形由其上下表面的压差引起，压差越大，变形量越大[23]。弹性片上下表面的压差取决于迷宫流道的能耗。滴头初始工作阶段，压力损失主要发生在迷宫流道，弹性片上下表面的压差随工作压力的升高而增大，弹性片在补偿腔中发生快速变形，补偿腔过流面积减小、压力损失增加。由于这一阶段水流能够从弹性片下表面竖直流出出口，过流面积相对较大，弹性片的变形不足以抵消水压对流量的影响[35]，因此滴头流量随工作压力升高迅速增长。当弹性片变形至接近凸台后，随着进口压力的增加，迷宫流道的压力损失增量减小，弹性片上下表面的压差增量也逐渐减小。弹性片在补偿腔和副流道中发生缓慢变形和微小变形，压力补偿滴头的出流截面非常小，补偿腔和副流道处压力损失明显增加，滴头流量随压力升高逐渐减小并趋于恒定。

实现压力补偿性能所需的最小补偿压力降低，可以降低滴灌系统所需的泵送压力[36]，从而实现低成本和低能耗的目标。要使压力补偿滴头在低压条件下发挥流量调节作用，就要控制弹性片的变形尽早进入微小变形阶段。若流道结构保持不变，减小弹性片的厚度或硬度，弹性片对压力的敏感性增强[28]，相同工作压力下弹性片的变形程度增大，弹性片接触凸台并进入微小变形阶段所需的工作压力降低；若弹性片性能保持不变，增加流道单元个数能够使迷宫流道的流动阻力增大[37]，水流流经通道的压力损失增加，弹性片上下表面的压差随之增大，弹性片易发生更大的变形并在较低工作压力下进入微小变形阶段。弹性片在副流道中的长期微小变形使流动阻力随压力升高而线性增加，滴头流量随流动阻力增加逐渐减小并趋于恒定，因此副流道处为压力补偿机制的关键触发区域，流量输出与副流道结构具有较强相关性。弹性片在副流道处的受力近似为简支的矩形膜，矩形膜的跨度为副流道的宽度，矩形膜的挠度为弹性片变形进副流道的深度[14]。当副流道深度一定、宽度减小时，相同压力下弹性片的变形程度减弱，弹性片变形至通道底部所需的最大压力升高，流动阻力的线性增长范围扩大；当副流道宽度一定、深度增加时，弹性片在通道中的容许最大挠度增加、可变形的压力范围增大，流动阻力的线性增长范围扩大；若保持流道结构不变，增大弹性片的硬度或厚度，弹性片对压力的敏感性降低[28]，弹性片在通道中发生变形的压力范围增加，流动阻力的线性增长范围扩大，压力补偿滴头的补偿区间随之增大。

滴灌系统水质不一，设计出具有目标流量和理想压力补偿区间的压力补偿滴头后，滴头的抗堵塞能力也是一项重要检验指标。近年来，加气和磁化处理广泛运用于含沙水的滴灌过程中[38-39]，后续可以继续开展不同加气和磁化强度条件下浑水滴灌对压力补偿滴头堵塞特性的研究。

4 结论

(1)构建了压力补偿圆柱滴头三维紊流状态下的流固耦合数值模型，通过模拟和实测0～300 kPa压力范围内滴头流量，得到模拟值与试验值的平均误差为12.32%，流固耦合计算方法能够准确预测压力补偿滴头流量。

(2)流动阻力主要发生在迷宫流道、压力补偿腔和副流道部位。迷宫流道阻力系数为2 987 Pa·h2/L2，其大小取决于迷宫流道的几何形状。压力补偿腔和副流道阻力随进口压力增加而增大，其大小取决于弹性片的变形程度。弹性片接触凸台前，补偿腔流动阻力系数增量为2 108 Pa·h2/L2，弹性片接触凸台后，副流道流动阻力系数增量为15 763 Pa·h2/L2。

(3)不同工作压力下弹性片变形-流动阻力-流量的关系为：压力场决定了弹性片两面的压差和变形，弹性片的变形改变了压力补偿腔和副流道的出流截面，出流截面减小使滴头内的压力损失增加，压力补偿滴头的流动阻力随之增大。由于较高的工作压力会产生更大的流动阻力，因此滴头流量随压力增加趋于恒定。

(4)实现压力补偿性能所需的最小补偿压力显著地受迷宫流道流动阻力和弹性片性能的影响，可以通过改变迷宫流道的结构或弹性片的硬度、厚度降低压力补偿滴头的最小补偿压力；为了实现压力补偿功能，滴头流动阻力需要随进口压力上升线性增加，可以通过改变副流道的结构或弹性片的硬度、厚度扩大阻力的线性增长范围、增大压力补偿滴头的补偿区间。