基于讨价还价模型的大数据资产定价研究

王重润 王文静 赵冬暖

【摘 要】 大数据作为数字经济时代重要的生产要素，其定价机制关系到数据资源的配置效率。由于大数据的异质性和形态及用途的多样性，目前的定价机制还不够成熟，传统的资产价值评估方法并不适用，期权定价、拍卖机制或者合作博弈理论成为大数据定价的探索方向。文章创新性地将参与方特征与平台参数加入讨价还价模型中，假定卖方的大数据成本和要价策略是私人信息，平台的影响则表现为买方的贴现因子变大，分别构建了完全信息及不完全信息下无交易平台、有交易平台三种情形的大数据定价模型，得到了对应的纳什均衡解，证明了不同信息结构下大数据定价效率损失，交易平台能够降低信息不对称从而提高定价效率。Matlab仿真实验证实了研究结论的合理性。研究补充和拓展了大数据定价的相关文献，对加快大数据交易平台建设、完善定价机制具有借鉴意义。

【关键词】 大数据； 资产定价； 讨价还价； 信息不对称； 虚拟仿真

【中图分类号】 F832.5；F275.5  【文献标识码】 A  【文章编号】 1004-5937（2023）06-0020-10

一、引言

大数据时代的到来标志着一场深刻的革命。世界各国非常重视大数据的发展，致力于促进大数据在各个领域的应用。国外比较知名的公司有Factual、BDEX、Infochimps、Quandl、Data plaza等。Factual是美国一家著名的大数据交易公司，其数据库存储着上千万个地理位置，旨在为需求者提供相关的地理位置信息；BDEX以真正提供实时的数据交换为卖点；Infochimps早期业务主要是提供数据市场服务和API接口，在用户超过一定数量的免费API调用额度后收取使用费，后来转型为大数据平台提供商；Quandl是一个针对金融和经济领域的大数据平台；Data plaza是日本著名的大数据交易市场，由富士通公司建立，核心业务是交易中介服务，提供的个人数据经过了脱敏处理，数据价格由数据量和数据类型决定[ 1 ]。

我国自2014年开始大数据交易平台建设。2015年8月，国务院印发《促进大数据发展行动纲要》，明确提出在全国培育大数据交易市场，同年11月，党的十八届五中全会提出把大数据建设作为新的国家战略。2020年4月，中共中央、国务院在《关于构建更加完善的要素市场化配置体制机制的意见》中提出，把数据补充进现有的要素市场，数据作为生产要素进行市场化配置。《2022年数据交易平台发展白皮书》显示，截至2022年8月，全国已成立44家数据交易机构。国内的大数据交易平台根据性质不同分为第三方和综合性数据交易平台（见表1）。第三方数据交易平台仅为数据供给与需求双方提供中介服务，旨在撮合双方数据交易，这种类型交易平台的数据来源是数据供给方，不涉及原始数据的收集、加工处理以及存储。而综合性数据交易平台则不单是作为中介为用户搭建数据交易桥梁，其服务内容更加丰富，包括为用户提供解决方案，同时该类平台自身可以采集数据，再进行加工处理存储，最终形成数据产品提供给用户。

大数据交易平台大多实行政府指导、社会参与、市场化运作的运营模式，交易机制以会员制准入方式为主，交易方式以线上交易为主，通过电子交易系统进行大数据交易。

随着各种类型的大数据交易平台的建立以及多元的数据交易服务的出现，驱动了全国数据要素流通，大数据交易规模越来越大。据《2021中国数据资产化工具市场研究报告》，2020年中国数据资产化市场规模为280亿元，未来五年复合增长率将达41%①。

从目前的发展现状看，大数据资产市场尚不成熟，数据交易规则、数据定价、标准规范等还在探索过程中，平台交易不活跃，线下交易居多，信息不对称比较严重，特别是大数据资产的定价机制不够完善，仍然依赖传统的资产评估方法比如成本加成定价法和收益法等。虽然在这些传统方法中加入了体现大数据特征的要素[ 2 ]，但还是具有局限性，不能充分体现大数据资产的价值，导致大数据资产的定价效率偏低，不利于大数据资产的交易。只有定价合理才能使大数据资产的价值最大化，才能引导数据资源实现最优配置。所以，大数据资产定价是亟待解决的难题。

二、大数据资产价值要素和市场结构

（一）大数据资产价值要素

大数据资产是在社会经济活动中产生的海量数据，为经济个体所有或者控制，可计量、具有应用场景、能产生新的价值的数据资源。大数据资产价值要素包括数据成本、质量、使用者的异质性、具体的应用场景等。

大数据的开发具有典型的规模经济效应。大数据的获取、清洗整理、深度挖掘以及数据库的管理与维护，构成大数据开发的主要成本。除了面向特定用户的定制大数据外，通用大数据经过预处理后具有易复制的特征，例如各种经济研究数据、行业数据、个人消费数据、病例数据、停车场数据，等等。大数据的开发成本不会因为使用者的增加而同比例增加，但边际成本却递减，且大数据的使用不具有排他性，这意味着大数据开发具有典型的规模经济效应。

大数据的质量影响其价值。影响大数据质量的因素可以概括为九个方面。（1）数据量。大数据资产的价值会因样本数据量的改变而改变，样本数量增加，有效信息越多，大数据资产的价值越高。（2）数据种类。大数据类型多样，例如医疗数据、金融数据、企业数据、能源数据、交通数据、商品数据、消费数据、教育数据、社会数据、社交数据、电商数据等，不同类型数据具有不同的用途，给需求者带来的预期收益不同，开发成本亦有很大区别，因此其价值也不同。（3）数据整合程度。数据时间跨度越大，数据越完整，蕴含的信息素越多，其价值越大。（4）数据准确度。数据价值靠挖掘，数据分析越彻底，针对該大数据资产的运用更加准确，创造的价值更大。（5）数据广度。某项大数据资产涉及的观测指标越多，样本范围越广，那么该大数据资产开发成本越高，使用价值越大。（6）数据时效性。经济社会在发展，大数据需要随着时间变化不断更新，才能满足变化的需求。如果大数据能够及时更新，其价值更高。（7）数据稀缺性。若某项大数据资产在交易市场上没有替代品，需求弹性小，则该大数据资产的价值越高[ 3 ]。（8）数据的生长性。若某大数据资产能够与市场上其他的大数据资产相结合，从而产生新的更有价值的大数据资产，那么该大数据资产的价值越高。（9）数据的外部性。使用某项大数据资产的用户越多，或者该大数据资产被多次使用，说明该大数据资产的价值更高。

大数据资产的价值还反映在具体应用场景上。首先，大数据产生价值的基础在于进行挖掘与分析，只有当大数据资产被运用到具体的场景后才能看到所带来的收益，以此判断其效用价值高低。其次，从大数据资产的使用价值视角分析，买方评价大数据资产价值的依据是其使用大数据资产前后形成的效用差。买方与卖方之间存在信息不对称，对大数据的处理过程、期望效用存在差异，卖方会高估大数据资产的价值，而买方会低估大数据资产的价值，出现“信息悖论”问题。即若买方在交易前对所交易的大数据资产了解得不够详细全面，则较难评估该大数据资产带来的价值，但如果不存在信息不对称，买方知道所有有关大数据资产的信息，则会降低对大数据资产的期望效用。因此，大数据资产的价值与购买者的异质性相关，相同的大数据资产对拥有不同信息资源购买者的价值存在差别。

（二）市场结构

大数据资产市场是典型的寡头垄断市场。从大数据供应商角度，互联网巨头和数据公司通过社交媒体平台的先发优势，形成了数字技术积累，大数据生产能够实现规模经济效应，这使得数据供应商取得了市场垄断地位，而需求者的价格弹性较小，消费者剩余被剥夺。从产品来看，与传统的数据库相比，大数据所涵盖的内容更多更丰富，不仅包括标准的结构化数据，还包括半结构化数据，以及图片、语音等非结构数据，大数据并没有标准统一的格式与模式，大数据的加工处理更加困难和复杂，这意味着大数据具有高度异质性。从信息结构看，数据供应商居于信息优势地位，买方与卖方处于信息不对称状态，交易过程存在“黑箱”现象。从市场容量看，根据《2021中国数据资产化工具市场研究报告》，中国大数据交易市场拥有数量巨大的用户需求，用户数量多达156万家，其中高需求用户数量达48万家。但是从实践情况来看，最终真正购买大数据资产并进一步应用和进行管理的用户规模不大，仅有1.4万家，占用户需求量的比例为2.9%，说明当前大数据交易市场客户开发率或者用户购买率较低。

（三）市场交易

大数据需求涉及多个行业、多个领域，例如金融机构、教育机构、各类企业、政府相关部门等。按照大数据交易的参与对象划分，有两种交易方式。一种是直接交易模式，买方可以与卖方签订长期合约获得长远收益；另一种是平台经济模式，第三方平台作为中介为双方提供交易空间，促进交易达成，从中收取服务费。通过平台进行交易又存在两种交易模式：一是C2B模式，指的是个人与企业之间的交易；二是B2B模式，即企业与企业之间的交易。

按照大数据产权交易方式分为三种交易模式。第一种模式是大数据使用权的交易。该模式下交易平台仅出售大数据的使用权，常用的交易方式有API接口、在线检索、数据终端。例如知网、万德、国泰安等数据库的查询使用权。通过这种交易模式交易大数据产品不限次数，并且大数据产品的价格也比较低。第二种模式是大数据收益权的交易。卖方为满足买方的定制化需求提供数据解决方案，买方在使用该定制化数据产品后产生的利润，需要依照之前双方的约定按一定比例转移给卖方。第三种交易模式是大数据所有权的交易。使用该种交易模式交易的大数据产品的知识产权受到更好的保护，例如大数据技术服务、定制化分析报告。

不论哪一种交易方式，寡头垄断的市场结构意味着大数据供应商能够在很大程度上影响市场价格。同时，由于大数据资产专有属性，买方数量比较少，这意味着买方也有一定的议价能力，特别是对于定制资产而言，尤其如此。目前传统的资产价值评估主要包括成本加成法、收益法和市场比较法等方法，但这些定价方法用于大数据资产价值评估时并不合适。大数据资产具有边际成本几乎为零的特征，成本法无法准确地计量大数据资产的成本；使用收益法估价时需要根据大数据资产用途进行预期收益计算，但大数据资产给需求方带来的预期现金流不容易得到，也很难准确估计；市场法更加适用于需求量大、交易相对活跃、可比类型多的资产评估，而大数据资产具有差异性大、交易时间短、交易数量少的特点，历史交易资料匮乏。因此基于讨价还价行为的定价机制，能够更有效率地反映利润最大化与效用最大化相互作用的结果，因而也能够更加真实地反映大数据资产的价值。下面本文将以讨价还价模型来分析大数据资产的定价策略及其均衡结果。

三、相关文献综述

国外学者基于供应商和用户视角，采用期权定价、拍卖机制等理论，从数据共享、产品异质性以及影响因素等维度研究了大数据资产定价问题。根据用户和产品的异质性及非结构化特点，将数据整合为不同的版本，结合用户任意查询次数进行差异化定价[ 4-5 ]。以上定价机制多由卖方主导，强调供应商的利润，缺乏对数据效用的考虑，如果考虑客户的支付意愿则能够为供应方创造更持久的利益[ 6 ]。另外，数据的稀缺性也会增加数据价值[ 7 ]。拍卖机制常被用来分析异质性大数据定价。为了鼓励买家透露真实的意愿价格，在拍卖机制中加入不允许买家后悔假设，则发现卖家对买家采取差异化销售策略有利于扩大销售收入[ 8 ]。

国内学者关于大数据资产定价的研究大体分为两个方向。一个方向是从财务角度分析影响大数据产品定价的财产属性[ 9 ]，利用重置成本法、数据资产预期收益法以及市场历史成交价格法来评估数据资产价值[ 10 ]。但由于大数据类型多样、数据资源稀缺，并具有复制低成本等特点，与知识产权、土地使用权等无形资产有很大区别，加之数据定价缺乏足够多的历史价格参考，所以用传统方法为大数据定价不够精确，于是很多学者开始思考另一个方向，即利用B-S期权定价[ 11 ]、合作博弈论与拍卖机制等理论，提出新的价值评估方法。例如，有学者在基础拍卖模型上加入大数据特征，扩展了Vickrey拍卖模型和序贯拍卖模型，讨论了卖方为实现利润最大化该选择哪种拍卖方式以及最优销售数量[ 12 ]。除了拍卖机制，还有学者采用合作博弈的讨价还价模型分析大数據资产定价问题。因为很多大数据资产具有异质性和专属性特点，需求和供给的对象比较明确，其交易过程具有讨价还价的特点，可以利用讨价还价模型来确定均衡价格。例如，在考虑成本价格、商品特性以及买方价格承受能力等因素的基础上，将竞标机制引入讨价还价模型中，建立基于竞标机制的鲁宾斯坦模型，研究两阶段、两个卖家一个买家进行讨价还价的定价问题[ 13 ]。还有学者运用重置成本法得出价格下限，用收益现值法得出价格上限，建立基于价格上限与下限范围内的三阶段讨价还价模型，研究“一对一”情形下的资产定价机制[ 14 ]。然而，因为价格上下限的估计是分别基于大数据卖方和买方的情况独立进行的，所以不能够保证重置成本法得到的价格一定比收益法得到的价格更小。

综上所述，国内外学者从多维度对大数据资产的价值评估展开了研究，提出了各种各样的评估方法，各有侧重。其中，基于合作博弈的定价方法主要强调了交易过程特点，但对非对称信息结构下交易平台的作用缺少深入研究。本文运用讨价还价模型，引入买方猜测概率来構造信息非对称结构下的收益函数，同时充分考虑交易平台的作用机制，引入平台参数，构建不同情形下的大数据资产定价模型并进行对比分析。本研究是对现有研究有力的补充和拓展，为大数据市场的发展提供了理论依据。本文随后结构如下：首先讨论完全信息条件下的竞争均衡，其次扩展到不完全信息的垄断情况，最后通过虚拟仿真实验检验模型效果。

四、完全信息下大数据资产价格讨价还价模型

（一）相关假设及参数设定

1.基本假设

假设大数据资产市场是完全信息的市场，买卖双方彼此知道对方的支付函数和行动策略。买方和卖方都具有经济理性，追求自身利益最大化，且风险中性，没有交易平台，买卖双方直接交易，交易过程中卖方先出价。

2.参数设定

V0：卖方对大数据资产的零利润价格（即最低要价）；u：买方对大数据资产的保留价格（即最高出价），服从均匀分布，为保证交易有意义，假设u≥V0；Pi1：卖方与买方其中一方在第i阶段的出价；？啄s：卖方贴现因子，0<？啄s<1，反映卖方的交易成本或者耐心；？啄b：买方贴现因子，0<？啄b<1，反映买方的交易成本或者耐心，随着谈判的回合增多，交易成本增大，双方的耐心较低，即贴现因子变小；ESi：卖方在第i阶段的收益；EBi：买方在第i阶段的收益。

（二）博弈过程

第一阶段：卖方出价P11。

在完全信息下，双方对对方的支付及其策略完全了解，卖方知道买方的保留价格u，此时卖方为了达成交易，其出价P11会低于买方的保留价格u，同时为了获得超额利润，其出价高于零利润价格V0。卖方ES1与买方EB1的收益如下：

ES1=P11-V0

EB1=u-P11

但是买方知道卖方的零利润价格V0，对于卖方的出价P1高于其零利润价格V0，如果买方选择拒绝交易，讨价还价进入第二阶段。

第二阶段：买方出价P21。

在完全信息下，买方知道卖方的零利润价格V0，此时买方为了达成交易，其出价P21不会低于卖方的零利润价格V0，此时买方出价P21=V0。在讨价还价的博弈过程中，随着谈判次数的增加，双方都需要付出一定的谈判费用，包括双方的时间成本、机会成本以及收集相关信息产生的沉没成本，所以谈判拖得时间越长，双方为此而承担的成本越多，收益越少，这种影响用贴现因子表示。此时，若卖方接受出价，则卖方ES2与买方EB2的收益如下：

ES2=？啄s（P21-V0）

EB2=？啄b（u-P21）

如果卖方选择拒绝交易，讨价还价进入第三阶段。

第三阶段：卖方出价P31。

此时卖方为了达成交易，其出价P31会低于买方的保留价格u同时高于第二阶段买方出价P21。若买方接受出价，则卖方ES3与买方EB3的收益如下：

ES3=？啄2s（P31-V0）

EB3=？啄2b（u-P31）

但是买方知道卖方的零利润价格V0，对于卖方的出价P31高于价格V0，买方会选择拒绝交易，讨价还价进入下一阶段。

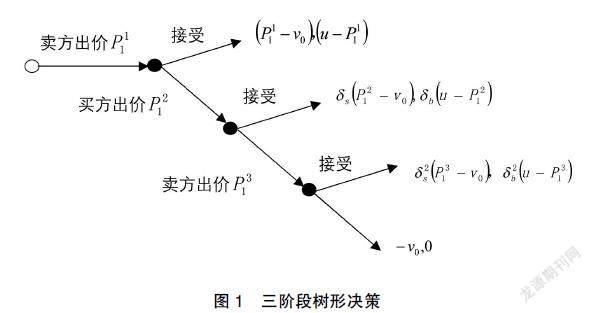
博弈如此循环下去，直到双方交易成功为止。图1展示的是三阶段讨价还价过程。

（三）模型求解

因为是完全信息博弈，卖方和买方都知道彼此的策略和愿意出价的程度。最终，对于买方来说，只要卖方的出价高于买方的保留价格，则买方选择不交易，此时卖方的收益为其机会成本（-V0），买方的收益为0；对于卖方来说，至少当买方的出价可以弥补其机会成本时，卖方才可能接受报价，此时买方的收益为（u-V0），卖方收益为0，这意味着达成交易是帕累托改进。因此，最终的定价为：

P*1=V0

即在完全信息条件下，均衡价格为零利润价格，即卖方得到零超额利润，而买方得到全部剩余。

五、不完全信息下大数据资产价格讨价还价模型

下面考察不完全信息的情况，即博弈双方知道对方的策略集合，但是事前不知道对方究竟采取什么交易策略及其相应的收益，区分无交易平台和有交易平台两种情形进行讨论。

（一）无平台情形

1.基本假设

放宽前面的假设，假定卖方与买方关于大数据资产的信息是不对称的。对于卖方来说，其掌握关于大数据资产的所有信息，因此其在讨价还价过程中每阶段的收益是已知固定的，而对于买方来说，其不了解大数据资产的处理难度以及成本，对大数据资产的信息知之甚少。因此卖方每阶段的出价到底是高要价还是低要价是私人信息，买方并不清楚，但是可以猜测卖方采取每种策略的概率，即在讨价还价开始时买方猜测卖方高要价的概率为？籽，或者是否接受买方报价的概率为q。在博弈的过程中，买方根据上一阶段的结果对下一阶段的概率进行修正。Pi2表示卖方与买方其中一方在第i阶段的出价。

2.博弈过程

第一阶段：卖方出价P12，买方决定是否接受价格。

对于卖方来说，出价高低是其私人信息，卖方的收益为出价减去保留价格，即P12-V0。对于买方来说，他只能猜测卖方高要价的概率并在讨价还价过程中进行修正。买方猜测卖方索要高价时，其收益为u-P12，买方猜测卖方索要低价时，其收益为u-V0。

买方以概率？籽猜测卖方采取高要价策略的情形下，买方EB'1的收益为：

以概率1-？籽猜测卖方采取低要价策略的情形下，买方EB''1的收益为：

因此，在第一阶段，卖方ES1和买方EB1所获得的收益如下：

如果买方拒绝价格P12，进入第二阶段博弈。

第二阶段：买方出价P22，卖方决定是否接受。

在价格水平P22，卖方的收益為ES2=？啄s（P22-V0）。买方根据上一阶段的结果对卖方是否接受出价的概率做出预测。假定买方以概率q猜测卖方会接受此报价，买方的期望收益为：

EB2=？啄bq（1-P22）

如果卖方拒绝了该阶段买方的还价，则进入第三阶段。

第三阶段：卖方出价P32，买方决定是否接受。

该阶段卖方的收益ES3=？啄2s（P32-V0）。买方根据上一阶段的结果对卖方采取高要价的概率进行修正，形成后验概率？籽'。买方EB'3的收益为：

EB'3=？籽'？啄2b（u-P32）

如果卖方采取低要价策略的情形下，买方EB''3的收益为：

在第三阶段，卖方ES3和买方EB3所获得的收益如下：

如果买方拒绝了该阶段卖方的出价，则进入下一阶段。这个过程一直进行下去，当且仅当其中一方接受了另一方的出价时谈判结束。

3.模型的求解

本文建立的模型是无限次的讨价还价合作博弈模型，不同于有限阶段讨价还价模型。有限次博弈可以将最后一阶段作为逆推归纳法的起始点，而无限次博弈没有可以作为起点的最后阶段，不能运用逆推归纳法求解本模型。Shaked和Sutton提出了一个解决无限次博弈问题的方法，证明从参与人1任何一个阶段开始的子博弈等价于从t=1开始的整个博弈[ 15 ]。这样就可以有限次博弈地逆推归纳法求解子博弈精炼纳什均衡。

为方便起见，本文选择三阶段讨价还价作为无限次讨价还价逆推的起点。在第三阶段，卖方收益为ES3=？啄2s（P32-V0），买方收益为EB3=？啄2b［？籽'（V0-P32）+（u-V0）］。再往回看第二阶段，如果避免进入第三阶段而导致不必要的损耗增加，买方在该阶段的最优策略即使得卖方在该阶段获得的收益ES2至少等于第三阶段中获得的收益ES3。即：

现在回推到第一阶段卖方出价。同样地，在此阶段中，如果卖方的出价P12使得买方的收益EB1小于第二回合中所获得的收益EB2，则买方肯定会拒绝，就会进入第二回合。所以，为了避免进入第二回合，卖方的最优策略是使其出价P12满足买方第一阶段的期望收益EB1至少等于第二阶段中获得的期望收益EB2。即：

对无限次合作博弈来讲，无论是从第一阶段开始还是从第三阶段开始，都是卖家出价，然后双方轮流出价，对于卖方来说最终得到的结果是一样的，因此有P12=P32=P2。整理式（3）得到：

由上式可知，只要？籽>？啄b？啄sq，即买方对于卖方出高价的先验概率足够大，那么与完全信息下的均衡价格V0相比，不完全信息—无平台情形下的均衡价格更高。可以看作是信息成本。在不完全信息下，由于买方对卖方处理大数据资产的过程、难度、成本等方面都不了解，卖方可以利用信息优势索取高价，获取更大收益。

4.均衡价格分析

（1）贴现因子。贴现因子在讨价还价的博弈过程中起着重要作用。在博弈论中，贴现因子表示为 ，指的是将未来收益折现到当前的一个系数，可见贴现因子的大小影响其收益，贴现因子越小，收益越低。贴现因子表示交易者的耐心程度，体现了其“时间偏好”，并且在一定程度上反映了双方的谈判能力。贴现因子较小的一方意味着其耐心程度较小，在谈判过程中希望更早地达成交易，而更有耐心的人可能获得更大的利益。

贴现因子被定义为是时间的减函数，即交易持续时间越长，贴现因子越小，越没有耐心。

对式（4）均衡价格分别求关于ts和tb的一阶偏导，得到：

由式（5）可知，如果？籽>？啄sq，那么随着买方的耐心程度降低，导致最终的成交价格越高，买方收益下降；从式（6）可知，随着谈判时间的延长，卖方贴现因子变小，耐心程度降低，导致最终的成交价格越低，卖方的收益越低。因此，在交易价格谈判过程中，双方为使自身利益最大，都希望降低时间成本，尽量提早达成交易。

（2）后验概率。后验概率是买方根据前一轮交易报价而对卖方策略行为的猜测，反映了双方的“合作偏好”。由于存在谈判的交易成本，合作对双方都有利，如果合作利益足够大，那么随着交易进程，买方猜测卖方接受低报价的概率q会提高。因此合作收益是影响后验概率的关键因素。对二者建立如下函数关系：

q=Q（a，M）

其中，a指的是双方达成合作获得的收益，M代表其他影响因素，比如上一轮的出价。根据上述分析得到：

同时将均衡价格对a求一阶偏导得到：

（二）有平台情形

1.研究假设

交易平台的参与使得双方信息不对称性降低，并且增加了大数据资产的流动性。买方通过交易平台对相关大数据资产的信息有了一定程度的了解，信息不对称程度降低，在谈判中变得更有耐心，提高了谈判能力，贴现因子变大。而卖方因为信息优势缩小，谈判能力下降，在谈判中变得更缺少耐心，贴现因子变小。如果以参数？兹表示平台的影响，？兹值越大，平台的影响越大，0<？兹<1，那么假定买方的贴现因子变大为？啄b/？兹，而卖方的贴现因子变为？兹？啄s，同时假设平台费用为常数，标准化为0，Pi3为卖方与买方其中一方在第i阶段的出价。讨价还价模型如下：

第一阶段：卖方出价P13，买方决定是否接受。

对于卖方来说，与前述相同，收益函数表示为ES1= P13-V0。对于买方来说，期望收益如下：

如果买方拒绝了该阶段卖方的出价，则进入第二阶段。

第二阶段：买方出价P23，卖方决定是否接受。

卖方的收益如下：

买方期望收益如下：

如果卖方拒绝了该阶段买方的还价，则进入第三阶段。

第三阶段：卖方出价P33，买方决定是否接受。

卖方的收益如下：

买方的预期收益如下：

整理得到：

其中，'表示买方对卖方出高价的后验概率。如果买方拒绝了该阶段卖方的出价，则进入下一阶段。当且仅当其中一方接受了另一方的出价时谈判结束。

2.模型的求解

按照前面的思路，首先看第三阶段，卖方收益为ES3=（？兹？啄s）2（P33-V0），买方收益为EB3=［？啄b/？兹］2［？籽'（V0-P33）+（u-V0）］。再往回看第二阶段，如果要避免进入第三阶段，那么买方在该阶段的策略是使得卖方在该阶段中获得的收益ES2至少等于第三阶段中获得的收益ES3，即：

现在回推到第一阶段卖方出价。为了避免进入第二回合，卖方的最优策略是买方在该阶段中获得的收益EB1至少等于第二阶段中获得的收益EB2，即：

由式（11）可知，只要？兹≥q？啄b，那么不完全信息下有平台的均衡价格P*3就会大于完全信息下的均衡价格P*1。由于q？啄b/？兹>q？啄b，那么有平台的均衡价格低于无平台的均衡价格P*2，这意味着不完全信息下有平台的均衡价格P*3介于完全信息价格P*1与不完全信息下无平台的均衡价格P*2之间。这说明，由于平台的加入，信息不对称程度降低，信息成本缩小，定价更接近于完全信息下的均衡价格。特别的，如果？兹=q？啄b，那么不完全信息下的均衡价格就等于完全信息均衡价格P*1，即V0。

六、数值模拟实验

为了验证模型的有效性，本文用Matlab 2018b进行数值模拟实验。首先根据不同的假设环境生成模拟数据，其次将模拟数据代入模型计算不同情况下的价格，并对影响均衡价格的因素进行分析。设定样本量为1 000。

假设买方对大数据资产的估价服从均匀分布，u～U（300，  1 000），其中300表示买方估计该大数据资产收集整理等一系列的处理成本，1 000表示买方估计使用该大数据资产所带来的效用即其最高出价。为保证交易有意义，假设u≥V0。？啄s和？啄b服从0～1上的均匀分布，即？啄s～U（0，1），？啄b～U（0，1）。在不完全信息且无交易平台下，为保证均衡价格的有效性，P2≤u，即？籽>1-？啄bq+？啄s？啄bq，这同时满足前面的理论假设？籽>？啄s？啄bq；在不完全信息且有交易平台下，根据理论分析，假设？兹>？啄bq。就贴现因子以及后验概率对不完全信息下无平台均衡价格的影响，根据理论假设？籽>？啄s。

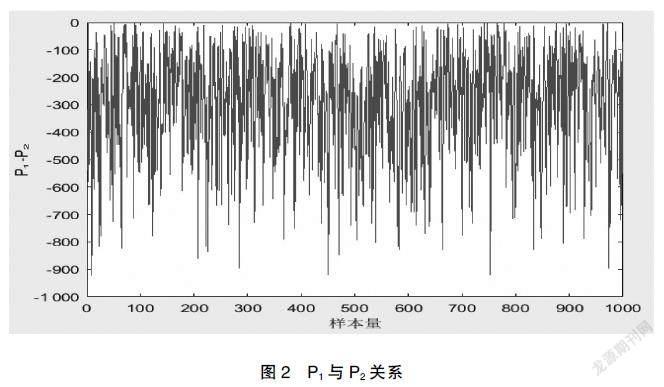
首先，看不完全信息且无交易平台的情境。其价格P2与完全信息下的价格P1之间的关系如图2所示。图2表示的是P1-P2得到的结果。可见，该曲线始终在0水平线的下方，说明完全信息下的价格P1小于不完全信息且无交易平台下的价格P2。

其次，考察不完全信息下有交易平台的情境。其价格P3与不完全信息且无交易平台情境下的价格P2之间的关系如图3所示。在图3中，P3-P2得到的结果曲线同样始终在0水平线的下方，说明不完全信息且有交易平台下的价格P3小于不完全信息且无交易平台下的价格P2。

进一步验证不完全信息且有交易平台下的价格P3是否大于完全信息下的价格P1。图4表示的是P1-P3得到的结果曲线。可见，该曲线也始终在0水平线的下方，说明P1P3，则P1

最后，再来看不完全信息均衡价格P2与卖方、买方贴现因子？啄s、？啄b之间的关系。图5表示价格P2与卖方贴现因子？啄s的关系，图6表示均衡价格与买方貼现因子？啄b的关系。可见：卖方的贴现因子与均衡价格呈正相关关系，即随着卖方贴现因子变小，卖方的耐心程度降低，导致最终的成交价格越低；买方的贴现因子与均衡价格呈负相关关系，即随着买方贴现因子变大，买方的耐心程度降低，导致最终的成交价格越低。与模型预期一致。

七、结论与政策讨论

本文利用讨价还价合作博弈理论，结合大数据资产交易特征，分别构建了完全信息条件下和不完全信息条件下的大数据资产定价的讨价还价模型，求解了纳什均衡结果，虚拟仿真实验证明模型具有合理性。得出四点结论：第一，在大数据资产定价中，均衡价格与信息不对称程度相关。基于大数据资产市场结构特点，信息不对称程度越大，价格越高。第二，在不完全信息且非对称条件下，买方对有关大数据资产的信息不了解，卖方具有信息优势，因此，相比完全信息条件下卖方定价更高。第三，交易平台的加入降低了信息不对称程度，表现为卖方的耐心程度降低而买方耐心程度提高，导致交易价格更接近完全信息下的价格。第四，提高交易效率，从而降低交易成本（包括时间成本），能够改善定价效率。

基于研究结论，结合大数据市场发展现状，提出以下政策建议：

第一，加快大数据交易平台建设。大数据交易平台是大数据资产价值生成、交易转让、安全保障的重要基础设施，建设大数据交易平台对培育数据要素市场、提高定价效率意义重大。建立大数据交易平台，首先，要做好顶层设计，根据区域经济社会发展战略和目标，明确数据交易平台的定位和运营模式，协调政府不同部门，实现数据互联互通，挖掘数字资源禀赋；其次，要构建平台交易规则体系，包括数据确权、数据采集、定价标准、互信机制、市场准入、数据安全标准等方面，使数据开发和交易有标准可循；最后，要培育市场主体，构建数字生活、智慧城市和产业互联网等规范化数据应用场景，吸引多元化数据交易主体参与，引导数据交易从线下、分散交易转向线上、集中化交易。

第二，建立完善的大数据信息披露与合规制度。平台应建立信息披露与监管制度，规定数据信息披露的内容、披露方式频率和披露范围，着力降低买卖双方掌握信息的不完全性和不对称性，帮助双方合理估价，营造公平的交易环境。建立合规审查机制，确保大数据权属的合法性、大数据使用的合法性，形成安全合规的交易链，防止政府、企业以及个人隐私数据的泄露，降低数据合规风险，并采用黑名单方式约束违法使用数据的企业，提高交易平台信任度。

第三，健全大数据交易市场管理机制。政府要推动建立数据采集、交易流通、开放共享的标准规范，细化技术标准和交易规则，丰富完善数据交易生态，促进交易效率和流动性提升。同时要加强数据的反垄断管理，打破信息壁垒，开放数据共享，形成数据互联互通机制。要加强数据安全、隐私保护，目前我国已经出台了《个人信息保护法》《网络安全法》和《数据安全法》，下一步应该加大对相关法律法规的落实力度，同时政府要推动平台企业开发相关区块链技术，保障数据流通有记录，明确数据权利归属，保障数据交易的真实、合规、安全。

【参考文献】

［1］ 王卫，张梦君，王晶.国内外大数据交易平台调研分析［J］.情报杂志，2019，38（2）：181-186.

［2］ 戴炳荣，闭珊珊，杨琳，等.数据资产标准研究进展与建议［J］.大数据，2020，6（3）：36-44.

［3］ LIN B R，KIFER D.On arbitrage-free pricing for general data queries［J］.Proceedings of the Vldb Endowment，2014，7（9）：757-768.

［4］ KOUTRIS P，UPADHYAYA PRASANG，BALAZINSKA MAGALENA，et al.Query-based data pricing［J］.Journal of the ACM，2015，62（5）：1-44.

［5］ NIU C，ZHENG Z，WU F，et al.Online pricing with reserve price constraint for personal data markets［C］.2020 IEEE 36th International Conference on Data Engineering，2020.

［6］ LIANG F，YU W，AN D，et al.A survey on big data market：pricing，trading and protection［J］.IEEE Access，2018（6）：15132-15154.

［7］ Li X，YAO J，XUE L，et al.A first look at information entropy-based data pricing［C］.IEEE International Conference on Distributed Computing Systems，2017.

［8］ AGARWAL，A.et al. A market place for data：an algorithmic solution［C］.Proceedings of the 2019 ACM Conference on Economics and Computation，2019.

［9］ 翟麗丽，马紫琪，张树臣.大数据产品定价问题的研究综述［J］.科技与管理，2018，20（6）：105-110.

［10］ 许宪春，张钟文，胡亚茹.数据资产统计与核算问题研究［J］.管理世界，2022，38（2）：16-30.

［11］ 李秉祥，任晗晓.大数据资产的估值［J］.会计之友，2021（21）：127-133.

［12］ 陈志注，王宏志，熊风，等.大数据拍卖的定价策略与方法［J］.中国科学技术大学学报，2018，48（6）：486-494．

［13］ 刘洪玉，张晓玉，侯锡林.基于讨价还价博弈模型的大数据交易价格研究［J］.中国冶金教育，2015（6）：86-91.

［14］ 赵丽，李杰.大数据资产定价研究：基于讨价还价模型的分析［J］.价格理论与实践，2020（8）：124-127.

［15］ SHAKED A，SUTTON J.Involuntary unemployment as a perfeect equilibrium in a bargaining model［J］.Economeitrica，1984，52：1351-1364.