一类具有双线性型两阶段结构的同类相食模型的动力学分析
2023-03-04蔺小林曹美琪李建全贾西北
蔺小林,曹美琪,李建全,贾西北
(陕西科技大学 数学与数据科学学院,陕西 西安 710021)
0 引言
同类相食是一种特殊的捕食行为,存在于某些特定种群之中,如浮游生物、鱼类、甲壳类动物、昆虫、两栖动物、爬行动物、鸟类等[1-5].研究表明同类相食可能对种群有直接的影响,例如它可以提高生存率、生长速度、寿命或繁殖能力[6-9].S.Biswas等[10-12]为了解同类相食的影响,他们提出并分析了一种针对食饵和捕食者的疾病系统,发现同类相食可能是一种自我调节机制.2022年,Kumari N等[13]建立并讨论了具有同类相食和中间捕食者的三重营养食物链模型,发现同类相食是维持种群平衡的重要调节因素.
阶段结构模型常常被用来刻画自然界中的种群,同类相食模型的研究也是主要建立在阶段结构模型的基础上.1999年,K.G.Magnusson等[14]研究了同类相食对结构化捕食-被捕食系统的不稳定影响,证明了同类相食率的增加可能会导致种群系统失去稳定性.2015年,Kang等[15]对于卵会被成熟个体所吞噬的同类捕食模型(*)进行了研究.
(*)
研究发现,该行为会促进种群内部的平衡.因此,将同类相食行为考虑到阶段结构模型中具有重要实际意义.2021年,Zheng等[16]考虑了具有两个时滞的阶段结构同类相食模型,发现捕食者的妊娠时滞可以使混沌现象消失并保持周期振荡.
本文在Kang等[15]提出的模型基础上,假设同类相食发生在种群的卵和成年两个阶段之间,即成虫会捕杀卵,以提升成虫的繁殖率,同时考虑卵的自然死亡率,建立了一类具有双线性型两阶段结构的同类相食模型(1).分别对存在和不存在同类相食行为的情况下对模型(1)进行动力学分析,比较发现同类捕食行为对种群发展带来的影响,丰富了对同类捕食行为在理论上的研究结果.
1 模型介绍
本文将种群个体的成长分为卵和成年两个阶段,并假设成虫会进行同类相食(即捕杀卵)以提升成虫的繁殖率(即幼虫的出生率),同时考虑卵的自然死亡率,建立如下数学模型:
(1)
这里E(t)表示t时刻卵的数量,A(t)表示t时刻成虫的数量,r为不存在卵制约情形下每个成虫的繁殖率,c为成虫捕杀卵后自身繁殖率增加的系数,ε表示卵对其出生率制约的系数,β是卵向成虫的转换率,d1为单个卵的自然死亡率,α为单个成虫对卵的捕获率,d2为单个成虫的自然死亡率.除a,c外,其他所有参数都为正数.当α>0,c>0时,表示成虫会捕杀卵,当α=c=0时,表示没有同类相食行为,此时模型(1)变为
(2)
定理1模型(1)在非负初始条件下的解保持非负性,区域
D={(E,A):0≤E≤E1,0≤A≤A1}.
为模型(1)的一个正不变集,其中

其次,由模型(1)的第一个方程,得
其中
因此
注1要满足0≤E≤E1,即r(ε+c)≥α,这表示在卵受到对其出生率的制约和成虫捕杀卵后对其自身繁殖率的提升双重影响下,最终成虫的繁殖率要大于等于成虫对卵的捕获率.结合实际情况这是显然成立的,自然界中成虫最终的繁殖率必须要大于等于成虫对卵的捕杀率,这样种群才会不断繁殖存活.在下面的讨论中,本文始终假设r(ε+c)≥α成立.
这意味着对于任意小的ε1>0,存在T>0,使得当t>T时,有E
A′≤β(E1+ε1)-d2A=d2(Aε1-A),
其中

故区域D是模型(1)的一个正不变集.
证毕.
2 模型分析
为了分析同类相食对种群生长的影响,在本节,首先分析无同类相食情形下,即α=c=0时模型(1)简化为模型(2)的动力学性态.然后再对模型(1)当α>0,c>0时全局性态进行分析.
2.1 无同类相食时模型的动力学性态
对于无同类相食情形下(即α=c=0)模型(2)的动力学性态.
对模型(2)直接求解方程组
(3)
可得方程组(3)的正解即对应模型(2)的平衡点.
定理2模型(2)不存在种群存活平衡点,且总有种群灭绝平衡点.
关于模型(2)种群灭绝平衡点的局部稳定性有如下结论:
定理3对于模型(2),当βr≤d2(β+d1)时,种群灭绝平衡点O1(0,0)在集合D内是局部渐近稳定的,当βr>d2(β+d1)时,种群灭绝平衡点O1(0,0)在集合D内是不稳定的.
证明:模型(2)在O1(0,0)处的Jacobi矩阵为
因此可知,平衡点O1(0,0)当βr
证毕.
定理4对于模型(2),当βr≤d2(β+d1)时,种群灭绝平衡点O1(0,0)在集合D内全局渐近稳定.
证明:为了证明种群灭绝平衡点O1(0,0)在集合D上的全局稳性定,定义Lyapunov函数为L1=βE+(β+d1)A,则L1沿模型(2)的解的全导数为


证毕.
2.2 具有同类相食时模型的动力学性态
对于存在同类相食的情形,模型(1)也总存在种群灭绝平衡点O2(0,0),为了确定模型(1)的种群存在平衡点,令模型(1)的左边为零,得到
(4)
方程组(4)的正解即对应模型(1)的种群存在平衡点.
由方程组(4)的第2个方程和第1个方程分别可以得到
(5)
(6)
当E≠0时,将(5)式代入(6)式有
(7)
令
F(E)=d2(1+εE)(β+d1)-
β[r(1+cE+εE)-αE(1+εE)]
根据模型(1)有正不变集D,F(E)=0在(0,E1)上的零点对应模型(1)的正平衡点E的坐标.于是,可通过判定方程F(E)=0在区间(0,E1)上根的存在性得到模型(1)正平衡点的存在性.
对函数F(E)直接计算,得
由于F″(E)>0,即函数F(E)的图形在区间(0,E1)上是一个凹的曲线.
当F(0)<0,即d2(β+d1)<βr时,函数F(E)在区间(0,E1)上有唯一零点.
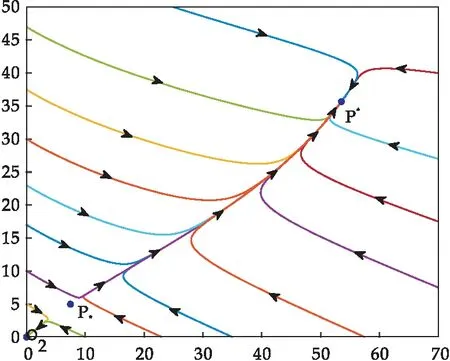
注意到当F(0)=0,且F′(0)<0时,即d2(β+d1)=βr,且α 注意到条件F′(0)<0且F′(E1)>0等价于不等式 因此,总结以上推导,关于方程F(E)=0在区间(0,E1)上的根的存在情形有如下结论: 定理5当下列条件之一满足时,方程F(E)=0在区间(0,E1)上存在唯一的根. (i)d2(β+d1)<βr; (ii)d2(β+d1)=βr且α (iii)d2(β+d1)>βr, 定理6当下列条件满足时,方程F(E)=0在区间(0,E1)上存在两个不同的根. d2(β+d1)>βr 根据定理5和定理6的推导过程,对其做如下注释: 注2(1)对于定理5中方程F(E)=0存在一个根的前两种情形,该根是一个单根,记为E*,其满足F(E*)=0. (4)由于α为单个成虫对卵的捕获率,一般来说α的值都比较小,在这种情况下容易证明定理5的条件(iii)和定理6的条件不相互矛盾. 对应于定理5和定理6,关于模型(1)正平衡点的存在性有以下结论. 定理7当下列条件之一满足时,模型(1)在区域D内存在唯一的正平衡点P*(E*,A*). (i)d2(β+d1)<βr; (ii)d2(β+d1)=βr,且α (iii)d2(β+d1)>βr,且 定理8当下列条件满足时,模型(1)在区域D内存在两个正平衡点P*(E*,A*)和P*(E*,A*). d2(β+d1)>βr, 关于模型(1)平衡点局部稳定性有如下结论: 证明:当d2(β+d1)>βr和d2(β+d1)<βr时种群灭绝平衡点O2(0,0)的局部稳定性证明同定理3.当d2(β+d1)=βr时种群灭绝平衡点O2(0,0)的局部稳定性证明如下: 当d2(β+d1)=βr时,做变换 模型(1)可变为 (8) 根据中心流形定理[17],可求得系统(8)在原点的局部中心流形为 进一步将上式代入系统(8)中的第一个方程得 (9) 根据(8)和(9),当rc=α时,原点为系统(8)是渐近稳定的;当rc≠α时,原点为系统(8)的鞍结点.如果rc≥α,则系统(8)在u>0一侧原点渐近稳定;如果rc<α,则系统(8)在u>0一侧为鞍点情形,是不稳定的. 综上所述,模型(1)的种群灭绝平衡点O2(0,0),当d2(β+d1)>βr或d2(β+d1)=βr且rc≥α时是渐近稳定的;当d2(β+d1)<βr或d2(β+d1)=βr且rc<α时是不稳定的. 下面讨论模型(1)正平衡点的稳定性. (10) 由方程组(4)的第一个方程可得 因此 由方程(5)和(7)可将其化简为 利用方程(7)可得 于是有 (11) 系统(11)在其原点附近可表示为 (12) 于是(12)可写为 (13) 再对系统(13)做变换 可得 (14) 其中 类似于种群灭绝平衡点O2(0,0)当d2(β+d1)=βr时的讨论,系统(14)在其过原点的中心流形退化为 (15) 证毕. 对于模型(1),记 Q=βE-d2A. 因此,模型(1)在区域D内无闭轨线.进一步,由于模型(1)的正不变集D的有界性,根据之前得到的其平衡点的局部稳定性,关于模型(1)的全局动力学有如下定理: (1)取参数r=0.5,c=0.2,ε=0.01,β=0.2,d1=0.3,α=0.25,d2=0.3,此时d2(β+d1)>βr,模型(1)的种群灭绝平衡点O2(0,0)是渐近稳定的,如图1所示. 图1 模型(1)不存在存活平衡点时的全局动力学性态 (2)取参数r=0.9,c=0.15,ε=0.01,β=0.2,d1=0.3,α=0.25,d2=0.3,此时d2(β+d1)<βr,模型(1)有唯一的种群存活平衡点P*(1.29,0.87).该平衡点P*是全局渐近稳定的,如图2所示. 图2 模型(1)存在唯一的种群存活平衡点P*时的全局动力学性态 (3)取参数r=0.55,c=0.15,ε=0.01,β=0.2,d1=0.3,α=0.05,d2=0.3,此时定理6的条件满足,模型(1)在区域D内有两个正平衡点P*(53.53,35.68)和P*(7.47,4.98).如图3所示. 图3 种群发展的最终状态依赖于初始条件时全局动力学性态,模型(1)存在两个正平衡点P*和P*时的情形 图4 种群发展的最终状态依赖于初始条件时的全局动力学性态,模型(1)存在唯一正平衡点时的情形 本文完整地分析了不存在同类相食行为和存在同类相食行为的两阶段结构模型平衡点的存在性、局部渐近稳定性和全局动力学形态.通过对比发现,成虫对卵的同类捕食会使模型的动力学性态变得复杂,产生鞍结点分支,使得种群的最终规模在一定条件下依赖于模型的参数取值.同时通过对相应结果进行数值模拟,直观地展示了种群在各种情形下的发展趋势.这些结果的得到,有利于人们合理控制有关种群的成长,对于保护有关种群结构有着重要作用.
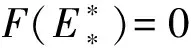
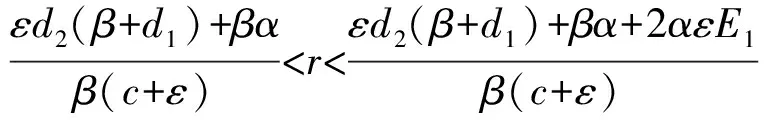






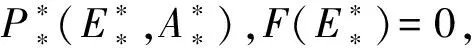


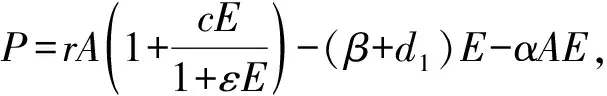






3 结论
