基于多策略黑寡妇算法的断路器全寿命周期成本优化
2023-03-04李维希李智轩吴富磊李潇雨
李维希,何 晋*,杨 凡,李智轩,吴富磊,李潇雨
(1.云南民族大学 电气信息工程学院,云南 昆明 650000;2.云南电网有限责任公司 楚雄供电局,云南 楚雄 675000)
0 引言
在“双碳”目标下,提高电力设备利用效率、延长电力设备使用寿命成为电力行业的共性需求[1].合理的运维策略、以运行风险为核心的电力设备全寿命周期优化管理体系,对提高设备可靠性、延长设备寿命、减小运营成本具有重要意义.
断路器是电力系统中控制和保护线路的重要开关设备,但断路器的维护成本和故障成本是初期投入成本的数倍[2].因此,兼顾可靠性及经济性将会成为今后预防性检修方案制定的方向.近年来,国内外学者对断路器的全寿命周期成本优化进行了大量研究.文献[3]在信息缺失的情况下,利用主元分析计算维护成本和故障成本,来建立费用最小优化模型.文献[4,5]将不同检修方案对应不同检修成本作为切入点对全寿命周期成本进行优化.文献[6]引入灵敏度系数,建立全寿命周期成本最小目标函数,并利用GAACS组合算法进行求解.文献[7,8]利用杜鹃算法进行参数寻优,前者以年均成本最小为目标函数,定量考虑检修时间、检修程度;后者以全寿命周期成本最小为目标函数,对大修次数进行寻优.上述研究大多以全寿命周期成本最小为出发点寻求最优检修方案,但在建模过程中忽略故障的随机性:不同故障类型发生的可能性不同.不同故障类型对应不同的检修方式,产生的检修成本也有差异,但大部分学者将检修成本模糊化处理,取其均值.
综上,本文兼顾断路器的可靠性及经济性提出一种基于多策略黑寡妇算法的全寿命周期成本优化方法.首先,综合考虑故障类型、故障检修方式、故障检修成本以及中断时间,将故障检修划分为三类;其次建立考虑故障检修方式的全寿命周期成本模型;再利用断路器运行可靠性、检修程度对目标函数进行约束;最后利用多策略黑寡妇算法对参数进行寻优.下文结合实例验证了该方法的有效性.
1 全寿命周期成本
1.1 预防性检修对断路器故障率的影响
断路器故障趋势同盆浴曲线相吻合,常用威布尔分布进行表示[9].威布尔分布的可靠性方程如公式(1)~(3)所示:
(1)
(2)
(3)
式(1)~(3)中:f(t)为故障概率密度函数;R(t)为可靠度函数;λ(t)为故障概率函数;β为形状参数;η为尺度参数.
随着在役年限的增加,断路器可靠性呈衰减趋势.为了减小故障率攀升对电力系统稳定性的影响,需对设备进行检修.断路器结构的复杂性导致检修时无法将部件逐一检修到位,且随着运行时间增加,各部件也会不同程度地老化.基于上述原因,预防性检修只能降低设备的故障概率但无法使设备“复新”.若断路器在役期间经历m次检修,每次检修程度为ki,其故障率变化曲线如图1所示,检修后的故障为[8]:

图1 检修后的故障率变化
(4)
式(4)中:λ(t)为检修后的故障率;λ0(t)为原始故障率函数;ki第i次的检修程度.
1.2 故障检修对全寿命周期成本的影响
断路器的故障检修方式主要分为返厂维修、现场更换故障部分、现场更换故障设备及外壳、设备替换、填充气体或替换密封装置、未检修就投入使用[10,11].不论该故障对断路器运行状态的影响是否严重,故障检修都存在以下可能性:一个简单动作就能使断路器恢复正常使用;需花费大量的时间成本及金钱成本,修复或更换断路器零部件.故障检修导致的设备停运会影响供电可靠性从而造成缺电损失[12],停机时间越长,单位缺电损失费用越高.综上,本文综合考虑断路器故障类型、发生概率、检修时间以及检修成本四个维度,将故障检修分为三类,具体内容见表1[4,10-12]所示.
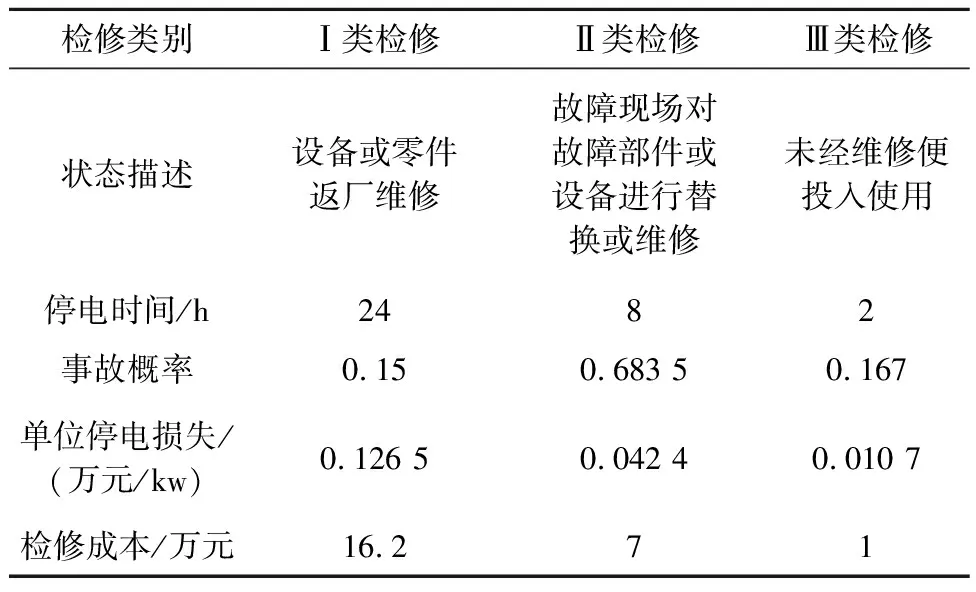
表1 故障检修类别及说明
1.3 故障期望指数
在不检修情况下设备的故障期望为:
(5)
据式(4)~(5)可以推测检修后的设备故障期望为:
(6)
本文将故障期望指数定义为:不检修情况下的故障期望与检修情况下的故障期望的差,同不检修情况下的故障期望的比值.利用故障期望指数来衡量预防性检修方案对断路器整个运行周期中故障发生概率的改善程度.故障期望指数FM可以表达为:
(7)
1.4 断路器全寿命周期成本
断路器全寿命周期成本综合考虑了断路器从设计、规划、投运,直至退役全过程的资金耗费,主要分为固定成本和动态成本.前者为设备购置等产生的一次性投入成本,后者为断路器进行日常维护等产生的附加成本.据国际电工委员会制定的IEC60300-3-3标准,可将断路器全寿命周期成本分为四部分,用公式表示为:
LCC=c1+c2+c3+c4
(8)
式(8)中:c1为运行成本;c2为检修成本;c3为故障成本;c4为广义折旧成本.
运行成本主要包括断路器在役期间的日常维护费用和环保费.随着运行年限增加,断路器状态逐渐劣化,所需运行成本也逐年增加.运行成本可以表示为:
(9)
式(9)中:c_base为断路器每年的基本运行费用;L为断路器在役年限;α为费用增长系数,常取0.05.
断路器的检修成本主要包括预防性检修费用、检修导致的中断损失,如公式(10)所示:
c2=Cprev+Coutage
(10)
式(10)中:Cprev为预防性检修费用;Coutage为中断成本.
预防性检修包括解体性大修和周期性小修,周期性小修只能维持设备当前状态对故障率的影响很小,因此本文中的预防性检修时间及程度主要指解体性大修的时间及程度,忽略周期性小修对故障概率的影响.据相关规程断路器周期性小修两年一次,检修成本可以表示为:
(11)
式(11)中:Cminor为小修成本;Coverhaul为固定大修成本;Cva为可变检修费用;ki为检修程度.
预防性检修导致的停电为计划性停电,不具备随机性,其中断损失主要为企业的停运损失,如式(12)所示:
(12)
式(12)中:K为检修次数;a为购售电价差;P为平均功率损失;t0为大修停电时间;tm为小修停电时间.
断路器的故障成本由故障检修费用和故障中断损组成.故障检修费用主要与检修方式有关;由于设备故障具备随机性及突发性,其中断损失不仅包括企业的停电损失,还包括用户损失.断路器故障成本可以表达为:
c4=Cfaul+Cbr
(13)
(14)
(15)
式(13)中:Cfaul为故障检修成本;Cbr为故障中断成本.式(14)~(15)中:n为故障期望;ci为检修类型;pi为该检修类型概率;ΔPtcm为检修时间为tcm时的单位负荷缺电损失.
广义折旧成本主要指断路器投运到退役,整个周期内所产生的一次性投入成本,包括前期的购置费、安装费、设备折旧价值、新旧设备交替成本.广义折旧成本可以表示为:
(16)
式(16)中:Ci为断路器购置费、安装费和其他费用所构成的前期投入成本;Cdp为断路器折旧价值,通常取购置费的5%;Cc为新旧设备交替成本;T为厂家设计寿命;L为断路器在役年限.
1.5 约束条件
电力设备的运行在满足经济性、可靠性的同时,还应符合一定的客观规律[7].检修后,运行可靠性R应大于在安全运行前提下的最低运行可靠性,即:
R≥Rmin
(17)
式(17)中:Rmin为断路器在安全运行前提下的最小运行可靠性,常取0.9;
设备部件老化的自然客观规律导致预防性检修效果呈逐渐减弱趋势,因此,预防性检修程度应满足以下条件,具体参数详见文献[7]:
0 (18) (19) 式(18)中:λ0(ti)、λ0(ti-1)为没有预防性检修的故障率.式(19)中:λ(t)为实际故障曲线;λbase(t)为理论故障曲线. 黑寡妇算法(Black Window Optimization Algorithm,BWO)是Hayyolalamh和Kazem在2020年提出的,以黑寡妇蜘蛛的整个生命周期作为数学模型的新型智能优化算法[13].由于BWO在工程优化问题上具备诸多优势,该算法也逐渐在特征选择、图像分割等领域崭露头角.如文献[14]采用具有五种优化策略的BWO算法寻找精度更高的特征子集.文献[15]提出了一种新的多层阈值图像分割算法,建立适当的目标函数并利用BWO算法求解得到最佳阈值集.文献[16]引入BWO算法,提高了ANFIS、SVM预测悬沙负载的精度.文献[17]利用BWO算法对深度卷积神经网络模型参数进行优化从而提高了从视频帧中检测人和物体的准确度.由此可见,BWO算法在工程优化中具备良好的应用前景. 雌性黑寡妇蜘蛛在交配期间或者交配完成后吃掉配偶.“物竞天择,适者生存”的自然筛选机制将体型较弱的子代淘汰,从而保留优秀个体,这种特殊的发育机制可被视作寻优过程.黑寡妇蜘蛛的生命周期可以分为种群初始化、繁殖、相食、变异四个阶段. 拉普卜特在《建成环境的意义—非言语表达方法》中认为研究环境意义的方式主要有3种:(1)运用语言模型,主要建立在符号学之上;(2)依赖于象征(symbols)的研究;(3)运用建立在非言语交流上的模型[15]22。余荫山房的建筑语言符号及其意义,主要体现在语言模型与象征方面。 首先,按式(20)~(21)进行随机初始化.初始化后的黑寡妇蜘蛛种群数为N,每个种群中含有D只黑寡妇蜘蛛. xid=rand(1,D)·(ub-lb)+lb (20) f(i)=fun(x1,x2,…,xd) (21) 式(20)中:ub、lb为上下限;式(21)中:f(i)为第i个种群的适应度值. 其次,进行种群繁殖.生殖率(procreate rate,PR)决定了参与繁殖的种群数量,在该种群中随机选择两只黑寡妇蜘蛛,适应度高的选作雌性,另一只选作雄性,通过公式(22)交配产生子代. (22) 式(22)中:yi、yj为交配后产生的子代蜘蛛;x_mother为雌性黑寡妇;x_father雄性黑寡妇;α为D维的随机数. 然后,同类相食,淘汰适应度差的黑寡妇蜘蛛,存活的蜘蛛数量由同类相食率(cannibalism rate,CR)决定.同类相食有三种类型:雌性黑寡妇蜘蛛在交配时或交配后吃掉配偶,自己被保留进入下一代,这一类被称作性同类相食;适应度好的个体吃掉适应度差的个体称为手足同类相食;子代黑寡妇适应度比母亲好,子代便会吃掉母亲,这种情况属于子食母同类相食. 最后,进行种群突变.突变种群数量由突变率(mutation rate,MR)决定,被选中的种群随机选取两只黑寡妇蜘蛛进行位置交换,如图2所示. 图2 BWO种群突变方式 一个生命周期结束,被保留的黑寡妇蜘蛛将进入下一个新的生命周期,直至满足停止条件. 2.2.1 拉丁超立方抽样种群初始化 初始化种群质量会影响算法的收敛速度及精度,本文采用拉丁超立方抽样种群初始化.拉丁超立方抽样(Latin hypercube sampling,LHS)是Makay等人提出的一种多维分层抽样的方法.它将区间[0,1]等距分成N个小抽样区间,在每个小区间内进行等概率随机抽样使得样本点能均匀覆盖在整个样本空间.随机抽样产生的初始化种群虽然分布在[0,1]空间,但较强的随机性会导致初始化种群的多样性差、搜索空间不合理. 由图3可知,随机抽样产生的种群初始位置较为密集,导致种群多样性较差,而LHS产生的初始化种群能均匀分布在搜索空间,丰富种群多样性. 图3 拉丁超立方抽样和随机抽样分布对比 2.2.2 基于精英母亲引导的子代生成机制 文献[18]将精英蜜蜂作为引导,对领域搜索方程进行改进从而提高了算法的搜索效率.在BWO算法中,繁殖产生的子代会影响算法的收敛速度,因此本文基于精英个体思想,提出一种新的子代生成机制.雄性黑寡妇蜘蛛作为起点,适应度高的雌性黑寡妇蜘蛛则为精英蜘蛛做方向引导,进而产生子代,使得子代适应度值能更快速接近全局最优解,从而提高算法的收敛速度.生成机制如公式(23)所示: y=a(xmother-xfather)+xfather (23) 式(23)中:y为黑寡妇交配后产生的子代;xmother为雌性黑寡妇;xfather为雄性黑寡妇;α为0~1的随机数. 2.2.3 自适应参数 在BWO中PR、CR、MR为固定常量,当PR、CR取值较大时,黑寡妇蜘蛛种群多样性丰富,具有较强的全局搜索能力,但在进行局部搜索时PR、CR仍取较大值会破坏当前种群结构,故,取固定常数不合理.因此,在算法前期PR、CR应取较大值,增强全局搜索能力,而在算法后期需进行精细化搜索时,PR、CR应取较小值[19].本文采用非线性双切正弦曲线对参数进行自适应调整.双切正弦曲线在迭代初期递减速度小,黑寡妇蜘蛛有足够的时间进行全局搜索,这样可以减小陷入局部最优的概率.迭代中期近似线性递减,局部搜索能力增强.迭代后期递减速度再次减小,进行精细化局部搜索最终确定全局最优解.自适应参数如式子(24)~(25)所示: (24) (25) 式(24)~(25)中:PRmax、PRmin为PR的最大、最小值,CRmax、CRmin为CR的最大、最小值,参考文献[19]并进行多次实验后取PRmax=0.8,PRmin=0.3,CRmax=0.7,CRmin=0.3;it为当前迭代次数;iter为最大迭代次数;双切正弦曲线的范围常取[-4,4][20]. 2.2.4 基于t-分布扰动和差分变异的变异策略 若寻求数学模型的最小值,当f(xi≤favg)时,种群正在向最优解聚集,此时MR过大会破坏当前解的结构.当f(xi)>favg时,种群分布较为分散,此时应增大种群突变概率使其向最优解进化.采用余弦自适应调整策略对MR进行调整[19]: (26) 式(26)中:MRmax、MRmin为MR的最大、最小值,最大值常取0.7,最小值常取0.1[19];f(xi)为种群的适应度值;favg为当前种群的平均适应度值;fmax为当前种群的最大适应度值. BWO突变方式过于简单,对多峰函数进行寻优时容易“早熟”.DE/best/1变异策略能帮助算法跳出局部最优,t-分布能保证种群多样性[21].因此本文采用多策略变异方式,如公式(27)所示: (27) 将迭代次数看作t-分布的自由度,在算法前期为柯西分布后期逐渐接近高斯分布.当rand>MR时,t-分布扰动能让黑寡妇蜘蛛逐渐向当前解靠近,随后在其临近区域展开搜索,不仅能增大搜索到全局最优解的概率,还能保证种群多样性.当rand 为验证改进策略的有效性,对Sphere和Rastrigin两个经典测试函数进行仿真实验,对比分析黑寡妇算法与改进黑寡妇算法的收敛速度及精度.为避免实验误差,设置相同的实验参数:黑寡妇种群数量为40;维度为30;最大迭代次数为500. 由图4可知,对单峰函数而言,MBWO收敛速度更快,适应度值的精度更好.适应度值精度达到10-6级,BWO算法需迭代150次,而MBWO仅需迭代33次,后者收敛速度更快.进行500次迭代后,BWO最大精度为10-6级,MBWO的最大精度可达10-155级. 图4 Sphere函数仿真迭代图 由图5可知,MBWO能在较少的迭代次数内使得适应度值近似直线下降,第33次迭代精度达到10-4级.反观BWO迭代170次左右适应度值精度才能达到10-4级.MBWO在第67次迭代时收敛到全局最优解0,BWO进行500次迭代后精度可达10-6,若继续增大迭代次数,收敛停滞且适应度值并不为0,则认为BWO在当前范围内陷入局部最优.由此可见,面对多峰极值函数,本文算法仍然能以较好的收敛速度及收敛精度收敛到全局最优解. 图5 Rastrigin函数仿真迭代图 本文以某电厂A厂家生产的断路器为例,对断路器全周期寿命成本、检修时间及程度进行分析.全寿命周期成本相关参数如表2所示,β=4.442 2,η=22.131 1,故障检修方式的相关参数可参考表1. 表2 全寿命周期成本参数 在同等约束条件下,分别采用MBWO、BWO、ABWO(Adaptive Black Window Optimization Algorithm,ABWO)[22]、改进SSA(Sparrow Search Algorithm,SSA)[23]、ASAPSO(Adaptive Simulated Annealing Particle Swarm Optimization Algorithm,ASAPSO)[20]对断路器年均全寿命周期成本进行寻优,各算法内部参数如表3所示,寻优过程如图6所示. 表3 各算法参数 图6 MBWO、BWO、ABWO、改进SSA、ASAPSO寻优图 由图6可知,当迭代500次时,迭代初期各算法均能在较短时间内收敛到某一较小值,但BWO、ABWO、改进SSA、ASAPSO在迭代中后期多次、反复出现收敛停滞现象,说明容易陷入局部最优解.反观MBWO,它在第139次迭代时收敛停滞直至迭代到第500次.虽然上述算法迭代多次后都能收敛到某一值,但综合考虑到计算精度和时间成本后,发现MBWO相对文中其他算法在该模型中有较好的表现.它不仅有较快的收敛速度,所得年均全寿命周期成本还最小.寻优所得的检修时间、检修程度、FM、年均成本见表4所示. 表4 全寿命年均成本优化结果 分析表4可得,MBWO寻优结果更接近全局最优解.将表中参数进行对比分析可以发现,尽早检修、检修程度较小或较晚检修、检修程度较大所得的年均成本均较小,发生故障的可能性也降低.当检修时间较早时,断路器劣化程度还不严重,无需较高的检修程度就能将断路器恢复至较好状态.但检修时间较晚时,断路器健康状态也较差,想要将断路器恢复至较好状态就需要增大检修程度.虽然各算法寻优所得的年均成本差距并不是很大,但是从企业盈利角度来看,利用MBWO寻优结果制定检修计划,需要投入的年均成本最小且设备发生故障的可能性更低. 本文将故障期望指数作为检修对断路器故障影响的评价指标,讨论不同检修方式对全寿命周期成本的影响.首先建立断路器全寿命周期成本模型并利用改进的黑寡妇算法进行求解,再将所得结果同其他算法进行比较,分析发现本文方法所得成本更小、故障期望指数更高,在兼顾投入成本的情况下能减小设备发生故障的概率.本文所得结果可以为电力部门定制检修计划提供一定的参考. 断路器是一个复杂系统,运行状态受众多因素影响.为制定合理的检修计划,本文下一步工作会将断路器健康状态作为参考依据,判定所需检修程度,从而避免过检修或欠检修,以达到合理利用资源,减小运行成本的目的.2 黑寡妇算法
2.1 黑寡妇算法概述

2.2 改进策略

2.3 改进算法性能测试
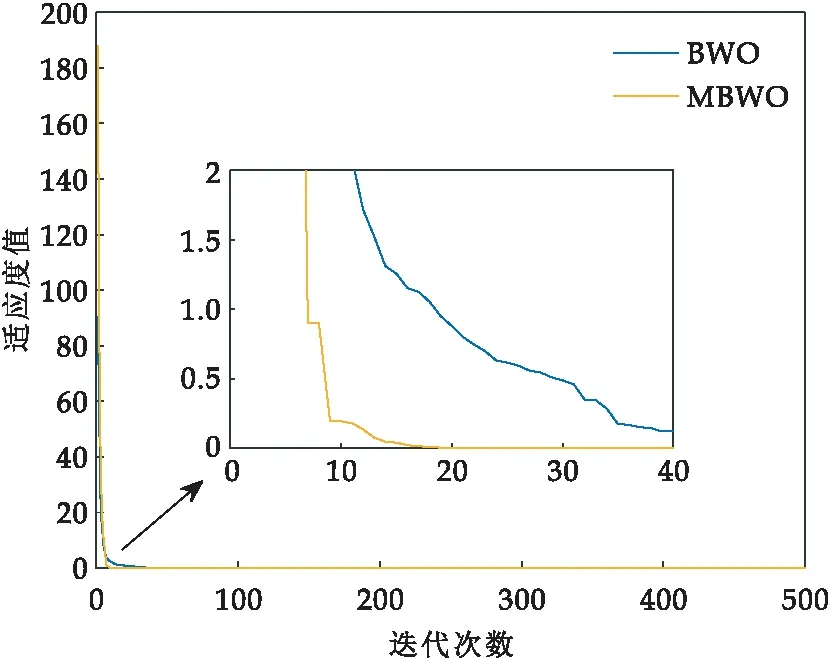

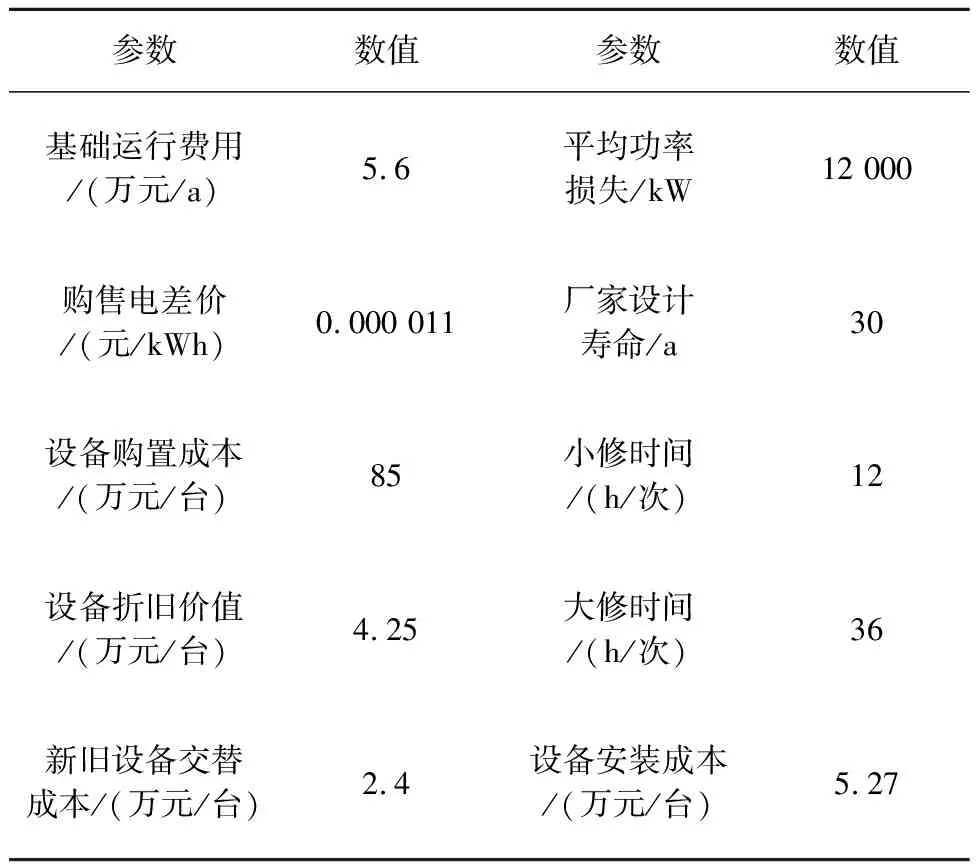
3 算例分析

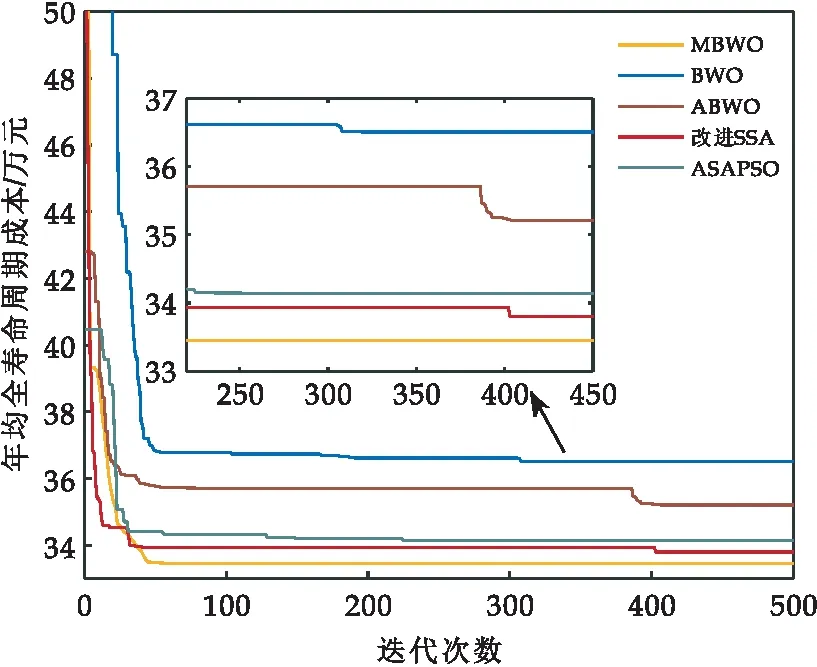

4 结论
