磁保持型航天电磁继电器性能提升与质量一致性设计

陈 昊 叶雪荣 梁慧敏 翟国富

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

0 引言

磁保持航天电磁继电器（Magnetic Latching Aerospace Electromagnetic Relay,MLAER）是一种典型的机电类元器件，具有灵敏度高、输入输出比大、发热小、抗干扰能力强、功耗低和体积小等一系列固态电子器件不可替代的优点，广泛应用于长征、神舟系列运载火箭和嫦娥系列飞船、高分系列卫星等航天装备的自动控制系统[1-2]。

然而，MLAER 目前仍然是所有航天装备用电子元器件门类中质量与可靠性最差的器件。据统计，近15 年共发生元器件性能与可靠性问题导致的装备延期与服役故障高达数百项，电磁继电器占比超过一半，MLAER 排序第一，因此MLAER 性能提升与质量一致性设计问题引起了广泛的关注[3-4]。

磁保持航天电磁继电器作为机-电-磁-热多物理场耦合作用的机电类元器件，其性能特征的准确计算是开展性能提升与质量一致性设计的重要基础与前提。基于有限元技术的虚拟样机仿真模型是一种常用的方法[5-7]，现有虚拟样机方法忽略了非线性永磁体充退磁过程中工作点和磁滞回线的变化，MLAER 的计算结果与设计差距较大。此外，其更大问题是存在严重的计算灾，难以直接应用于需要大量样本计算的质量一致性优化。

为了提高MLAER 的计算效率，学者们提出等效磁路模型[8-9]，这种方法在一定程度上解决了计算效率的问题，但由于漏磁通、漏磁导及磁饱和程度难以精确评估，故计算精度难以满足需求。针对虚拟样机计算效率低和磁路法精度差的问题，学者们提出了代理模型方法[10-14]，响应面代理模型虽然建模简单但计算强非线性性能特征时误差较大。径向基代理模型具有较强的高维非线性拟合和局部逼近能力，不会出现局部极小问题，但其对样本数量和样本数据质量要求较高。克里金代理模型在相同样本数据点下可显著提升高维非线性性能特征的建模精度，但其对样本数据的有效性非常敏感，易在局部产生较大误差。更重要的是，上述代理模型降低性能特征计算对硬件的需求，提高了计算效率，但这些代理模型大都以虚拟样机计算结果为基准进行建模，虚拟样机计算本身在计算MLAER 时便存在计算精度差的问题，依赖样本质量的径向基和克里金方法无法从本质上提升性能特征的计算精度。

代理模型提高了MLAER 的计算效率，但在性能优化与质量一致性设计上需要解决MLAER 衔铁中位、动作电压参数、动作时间参数、力学性能、热学性能、电寿命等多目标特征之间相互制约。因此学者们提出了一些多目标智能寻优方法[15-17]，这些智能寻优方法虽然进一步提高了MLAER 的寻优效率并在一定程度上实现了多目标综合优化，但只是在海量方案中随机遴选满足预设要求的设计方案，并不清楚设计参数组合与MLAER 性能特征之间的作用机制，寻优迭代较为盲目、耗时较长且迭代收敛鲁棒性不佳。

本文充分考虑非线性各向异性永磁体充退磁过程中的局部磁滞效应，基于斯通纳-沃尔法斯模型[18]和Preisach 模型[19]，建立MLAER 局部磁滞模型，进而建立可准确计算其静、动态特征的虚拟样机模型；在此基础上，借鉴模糊混沌展开替代建模方法适用于强非线性、径向基函数替代建模方法逼近能力强的特点，将样机实测结果引入替代建模，较好地解决了虚拟样机计算速度慢、容易不收敛及替代模型精度低的问题。在此基础上，明确MLAER 设计参数与性能特征之间的作用规律，并通过改进差分进化多目标寻优算法，进一步提高质量一致性设计的迭代寻优速度、收敛性和鲁棒性，从而实现多目标优化设计，提升综合性能，改善质量一致性。以双磁钢差动式MLAER 为例进行消除衔铁中位、降低动作电压、提升电寿命和提高质量一致性等优化设计，验证本文方法的有效性。

1 磁保持型航天电磁继电器性能提升与质量一致性设计方法

1.1 MLAER 性能提升与质量一致性设计概述

本文针对MLAER 存在非线性和输出过零特性导致虚拟样机收敛性差、计算精度差、衔铁中位、动作电压高及电寿命低等问题，提出一种适用性强、可用于各类电磁继电器寻优过程的质量特征计算和一致性多目标设计方法。分析MLAER 中非线性各向异性永磁体的实际工作点，基于实际工作点使用S-W 模型计算得到永磁体的磁偶极子的矢量化信息，将矢量化信息代入Preisach 模型计算得到永磁体局部磁滞回线模型。将局部磁滞回线代入Flux 电磁系统样机模型，计算得到MLAER 电磁吸力（矩）和磁链，在Ansys 中建立触簧系统柔性运动多体的柔性体机构，在Adams 中建立触簧系统机械反力（矩）计算模型，在Matlab/Simulink 通过数据接口将吸力（矩）传递给动力学软件开展动作过程分析，同时动力学软件将求得的衔铁（角）位移等动力学参量反馈给Matlab/Simulink，最终建立MLAER 虚拟样机模型。制作半开放式实物样机，实测继电器动作电压、吸合时间、释放时间等性能参数，对比验证虚拟机样机计算精度。

随后在继电器各个参数设计允许范围内使用均匀抽样设计生成样本点，虚拟样机模型计算得到各个样机的性能特征，利用模糊混沌展开代理建模方法得到各个设计参数和性能特征之间的数学关联关系作为代理模型的基函数。模糊混沌展开得到的基函数模型与实物样机之间往往存在一定偏差，使用最速曲率方法计算性能参数误差较大的位置，以其对应的设计参数为基准，制造相应的实物样机。并以实物样机实测结果与模糊混沌展开基函数计算结果的差值作为插值节点，使用径向基函数方法得到误差补偿函数，模糊混沌展开基函数与径向基误差补偿函数组成本文的MLAER 性能特征代理模型。

代理模型的建立提高了MLAER 的性能特征计算与分析的精度和效率，由于质量一致性设计需要的大量样本及多目标之间的相互制约，完成性能提升和质量一致性设计仍需花费较多的时间和占用大量的计算资源。以吸反力配合特征和分段动能为内核，分析MLAER 性能特征和质量一致性的形成机制，据此建立可同步解决衔铁中位、动作电压超差、电寿命不足和质量一致性问题的多目标优化模型。与此同时，为了进一步提高迭代优化过程的效率，本文改进多目标差分进化算法，采用多种群策略、自适应种群权重以及小生境思想，使其更为适合MLAER 优化，避免寻优迭代过程陷入局部最优，保证性能提升与质量一致性设计的精度和效率。本文所提方法的总体流程如图1 所示。

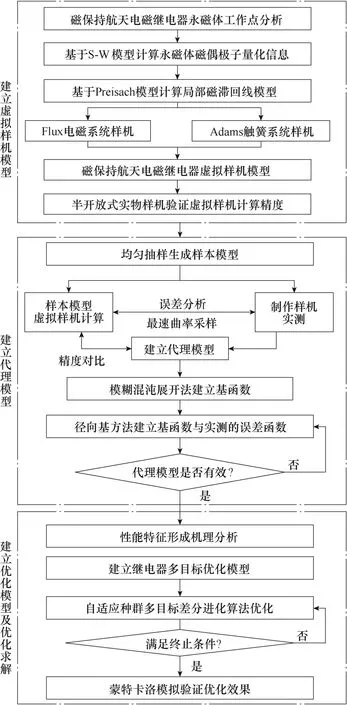
图1 优化方法总体流程Fig.1 Processes of the design optimization method

1.2 虚拟样机建模方法

1.2.1 非线性各向异性永磁体工作点分析

永磁体工作点迁移模型示意图如图2 所示。当非线性各向异性永磁体充磁饱合时，其工作点位于Q0处，在退磁外磁场作用下，其工作点沿去磁曲线迁移，此时永磁体在继电器中工作点将会迁移至Q1处，也即充磁时永磁体工作点沿图2 中回复线进行迁移（绿色线条所示）。同理，退磁时永磁体工作点将会顺着第二象限的去磁曲线迁移。若对永磁体进行非饱和退磁，假设退磁到外磁场强度为H轴下方H2处，此时，永磁体的工作点将沿图2 中非饱合退磁磁滞回线进行迁移（蓝色线条所示），使用仿射变换可以计算得到不饱合退磁时的永磁体工作点Q2。

图2 永磁体工作点迁移模型示意图Fig.2 The schematic diagram of the permanent magnet working point migration model

1.2.2 非线性各向异性永磁体局部磁滞回线计算

由S-W 方法可知[16]，单轴单畴磁性微粒的磁特性可表示为

式中，E为单轴单畴磁性微粒的自由能密度；Kv、MS、H分别为单轴单畴磁性微粒的各向异性磁系数、工作点S=Q2对应的磁化强度及外加磁场的场强；τ为外加磁场与易磁化方向的夹角；θ为工作点对应的磁化强度与易磁化方向的夹角。

由式（1）可知，工作点S=Q2对应的磁偶极子矢量方向可由式（2）求得。

在永磁体工作点对应的磁性微粒磁偶极子矢量方向已知的前提下，使用改进Preisach 模型可知[19]，永磁体宏观磁感应强度B(H)为

式中，Hsat为饱和磁场强度；二元函数μ(α,β)为偶极子正向翻转阈值α和负向翻转阈值β的分布密度。

由式（3）可知，永磁体的局部磁滞回线表示为

式中，Bt(H)为极限磁化曲线；Bd(H)为下降支；Bu(H)上升支；B1和H1为偶极子反转点坐标；为起始于(H2,Q2)上升支局部磁滞回线；为起始于(H2,Q2)下降支局部磁滞回线。

1.2.3 MLER 虚拟样机模型建立

应用三维建模软件UG、SOLIDWORKS 等建立继电器三维零件模型（衔铁、轭铁、铁心、静触点、动簧片等）以及装配样机模型。在有限元分析软件Flux 建立MLAER 的电磁吸力特性计算模型，对模型中衔铁与轭铁缝隙处进行细分网，空气球内部其他部分进行粗分网，充退磁后的永磁体赋予1.2.2 节计算得到的局部磁滞回线，铁磁材料赋予相应的软磁材料磁化曲线，在立方体边界设置磁感应线在边界区域与立方体边界平行，即将矢量磁位设置为常数0，计算衔铁长、衔铁宽、衔铁厚度、轭铁厚度、永磁体长、永磁体厚度及永磁体剩磁与电磁吸力之间的关系，实现电磁吸力特征（电磁吸力、磁链等）的准确计算。在Ansys 软件中建立触簧系统动簧片柔性多体模型，将柔性多体模型导入运动分析软件Adams 中，设置静触点直径、动簧片厚度、动簧片长度、动簧片宽度、动簧片等效刚度、初压力、触点间隙等输入参数，设置运动边界条件，实现继电器衔铁位移-反力（矩）特征的计算；然后在静态电磁吸力力矩数据和磁链数据的基础上，在 Matlab/Simulink 搭建继电器静/动态特征控制与计算框架，进而实现继电器虚拟样机模型的建立，计算继电器动作电压、衔铁是否中位、触点分断速度、动作时间和触点闭合速度等静动态性能特征。建模与数据交换流程如图3 所示。制作半开放式实物样机，实测继电器动作电压、吸合时间、释放时间等性能参数，对比验证虚拟机样机计算精度。

图3 虚拟样机建模与数据交换流程Fig.3 Virtual prototype modelling and data exchange process

1.3 代理模型建模方法

代理模型的核心思想是搭建一个隐式或显式的多项式来代替MLAER 隐藏的结构功能模型。如何提高代理模型的计算精度和效率是实现继电器性能提升和质量一致性设计的前提。本文针对该类型继电器非线性强、性能特征过零等特点，提出一种可适用于各类继电器迭代优化过程的快速计算方法，有

式中，B(·)为基函数，可由模糊混沌展开得到；R(·)为误差修正函数，可由径向基函数根据基函数计算与实物样机测试结果之间的误差得到。

本文基函数以虚拟样机模型计算结果为基础，通过均匀抽样生成样本，建立性能特征响应Y和变量参数x1,x2,…,xn之间的量化关系，采用式（6）所示的模糊混沌展开多项式。

式中，P为正交多项式的项数，计算公式为，p为满足替代建模精度要求的展开阶数，p一般取3,5,7。

模糊混沌展开的关键在于构建合理的多维Legendre 正交多项式x和高效求解模糊混沌展开的系数φ。本文将x等效为一个与Hermite 类似的多项式，有

式中，φ为整数序列；L可由式（8）所示的递推关系计算。

展开系数φ为

模糊混沌多项式展开得到的基函数B(·)，适用性较强，而且求解继电器性能特征速度较快，比较适用于计算量大的场景，但模糊混沌方法在计算非线性程度较高MLAER 时误差较大。对此，本文提出一种基于径向基函数方法得到的误差补偿函数提高继电器性能特征的计算精度。

在准确值与基函数的差值满足白噪声分布的前提下，计算继电器性能特征曲率变化情况，确定曲率最速下降区域，制作该区域的实物样机，并实测性能特征。同时使用基函数计算补偿样本的性能特征，以实测结果与基函数计算结果的差值作为插值节点，关联相应的函数类型为高斯类型，应用径向基函数方法得到误差补偿函数R(·)。基函数和误差补偿函数共同构成了本文的代理模型。

1.4 磁保持航天电磁继电器多目标优化方法

1.4.1 电磁继电器多目标优化原理

MLAER 两侧吸反力配合特征是对称的，因此本文仅以吸合位置的左半段性能特征为例进行优化目标与优化原理分析，MLAER 两侧吸反力配合特征示意图如图4 所示。

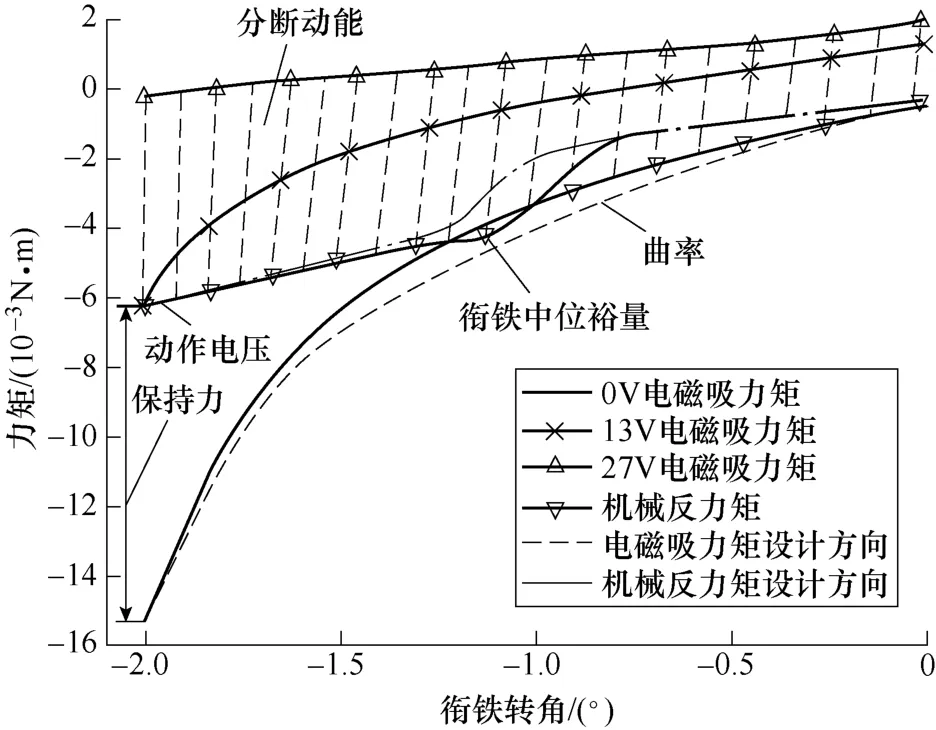
图4 MLAER 质量特征配合示意图Fig.4 The schematic diagram of the suction-reverse force characteristic fit about MLAER

可见，MLAER 性能提升与质量一致性设计主要针对其耐力学性能（用保持力表征）、衔铁中位、动作电压和电寿命（用分断速度和分断动能来表征）。其中，保持力和动作电压可通过转角为-2.1 °时的0 V 电磁吸力、某一电压下的电磁吸力与机械反力做差来计算。

衔铁无中位即是在所有转角范围内0 V 电磁吸力与机械反力仅有平衡位置一个交叉点，可通过适当增大触簧系统触点间隙、初压力和降低触点超行程、自由行程来优化。此外还可以通过降低0 V 电磁系统的曲率，使电磁吸力与机械反力不发生过早交叉，由于曲率不易直接计算与表征，本文提出0 V吸力曲线形态系数δ，0≤δ≤1，形态系数δ与 0 V电磁吸力曲线的凹凸度成反比，有

式中，MF为永磁体力矩；Mtotal为电磁系统总力矩；，W0为永磁体截面积，W为气隙总截面积；μr为相对磁导率，，μ为永磁体磁导率，μ0为真空磁磁导率；，Δ1为左侧工作气隙长度，Δ2为右侧工作气隙长度；ς为形状因子，是永磁体的等效内磁导与气隙磁导之比。

可见，形态系数与永磁体截面积、轭铁与永磁体距离成反比，与永磁体长度成正比。因此在消除中位设计时可以适当降低永磁体截面积、轭铁与永磁体距离，增加永磁体长度。

课题组以往研究表明，提高电磁继电器的触点分断速度，可以显著减弱触点电侵蚀、提升其电寿命[20]。触点分断速度是吸反力配合的结果，难以通过简单的电磁吸力和机械反力分析获取，本文考虑分断速度与继电器动作过程能量积累之间的关系，采用式（12）所示的分断动能来量化表征分断速度，通过提升分断动能改善MLAER 的电寿命。

式中，ψ为继电器线圈磁链；U、i、R分别为继电器线圈电压、电流及电阻；l、ω分别为衔铁角位移和角速度；Ebreak为继电器分断动能；J为衔铁部分的转动惯量；ρ、r和dV分别为质量分布连续钢体的密度、转动钢体的转矩、质量分布连续钢体的体积元；Fatr(t)为相应时间的吸力值；Fcon(t)为相应时间的反力值；Δl为弹性簧片的位移；ψ0、l0分别为t=0 时刻的线圈磁链和衔铁位移。

可见，MLAER 的分段动能与转矩、吸力和反力值等相关，要提升其分断动能可以通过适当增加转矩、触点超程、自由程、触点初压力和簧片等效刚度，降低触点间隙、永磁体剩磁等。

1.4.2 电磁继电器多目标优化寻优方法

上述分析表明，MLAER 多个性能提升之间是相互制约的，因此，在明确性能提升与质量一致性设计技术路径的同时，还应该研究相应的多目标优化方法，解决多个目标之间的掣肘并提升优化效率。

本文针对差分进化算法在解决多维、强非线性优化问题寻优效率低、精度差的问题，提出自适应种群策略的多目标差分进化算法。采用如式（13）和式（14）所示占优种群与非占优种群不同的变异个数和变异策略的多种群策略。

式中，P*为Pareto最优解集；nMut为该个体变异交叉个体数；N为总的种群个数；G为当前种群代数；Gmax为种群最大代数；ℓ 为常数，。

同时，为了确保寻优解集的均匀性，基于小生境思想对当前种群所有个体的密集程度进行分析与计算，有

2 磁保持型航天电磁继电器性能提升与质量一致性设计实例

本文针对广泛应用于运载工具、卫星载荷和星务计算等的双磁钢MLAER 存在的衔铁中位、动作电压超差和电寿命过低等潜在归零风险进行优化，综合提升其性能与质量一致性。该电磁继电器的电磁系统和接触系统结构如图5 所示。

图5 双磁钢MLAER 结构示意图Fig.5 Schematic of the dual magnet MLAER

该继电器静动态虚拟样机模型如图6 所示。

图6 MLAER 虚拟样机模型Fig.6 The relay virtual prototype model MLAER

使用图 2 和图 3 所示的虚拟样机模型计算MLAER 的静态电磁吸力（矩）、机械反力（矩）、动态动作电压、分断速度等性能特征，并将计算结果与实测结果进行对比，结果见表1。

表1 虚拟样机计算与实测对比结果Tab.1 The comparison results of virtual prototype model with measurement

可见，本文所提方法建立的MLAER 静动态性能特征最大计算误差仅为5.01 %，计算精度完全可以满足MLAER 性能提升与一致性设计的需求。

虚拟样机计算模型计算结果虽然精度较高，但其每个样本的计算都要5 h 以上，计算效率较低。采用本文所提的代理模型建立方法，设计参数允许最小值、中心值和最大值为三个水平，使用均匀抽样建立虚拟样机模型并计算相应的性能特征，使用模糊混沌展开建立代理模型基函数模型，随后使用最速曲率下降计算出误差较大的区域，制作相应的实物样本。计算基函数与实测结果之间的误差，使用所提的径向基函数方法得到代理模型的误差补偿函数模型，以机械反力（矩）和动作电压（从100台样机抽取20 台将本文模型计算结果与自适应克里金方法进行对比）为例，结果如图7 所示。静动态性能特征的计算结果与实测对比见表2。

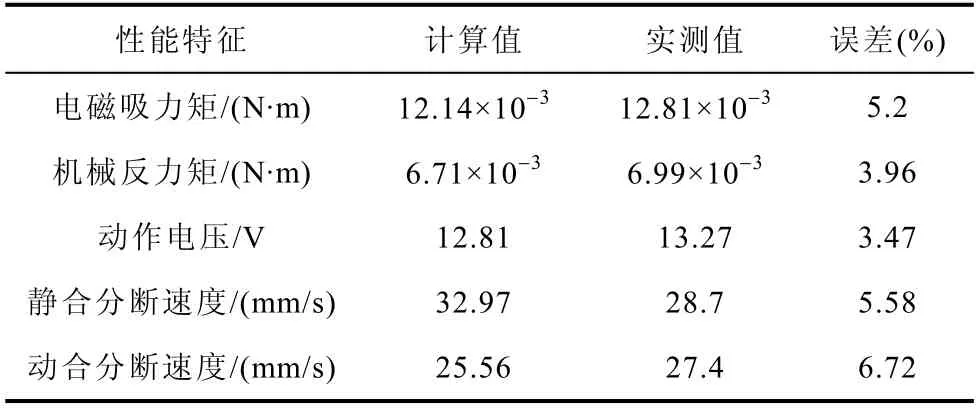
表2 代理模型计算与实测对比结果Tab.2 The comparison results of surrogate model with measurement

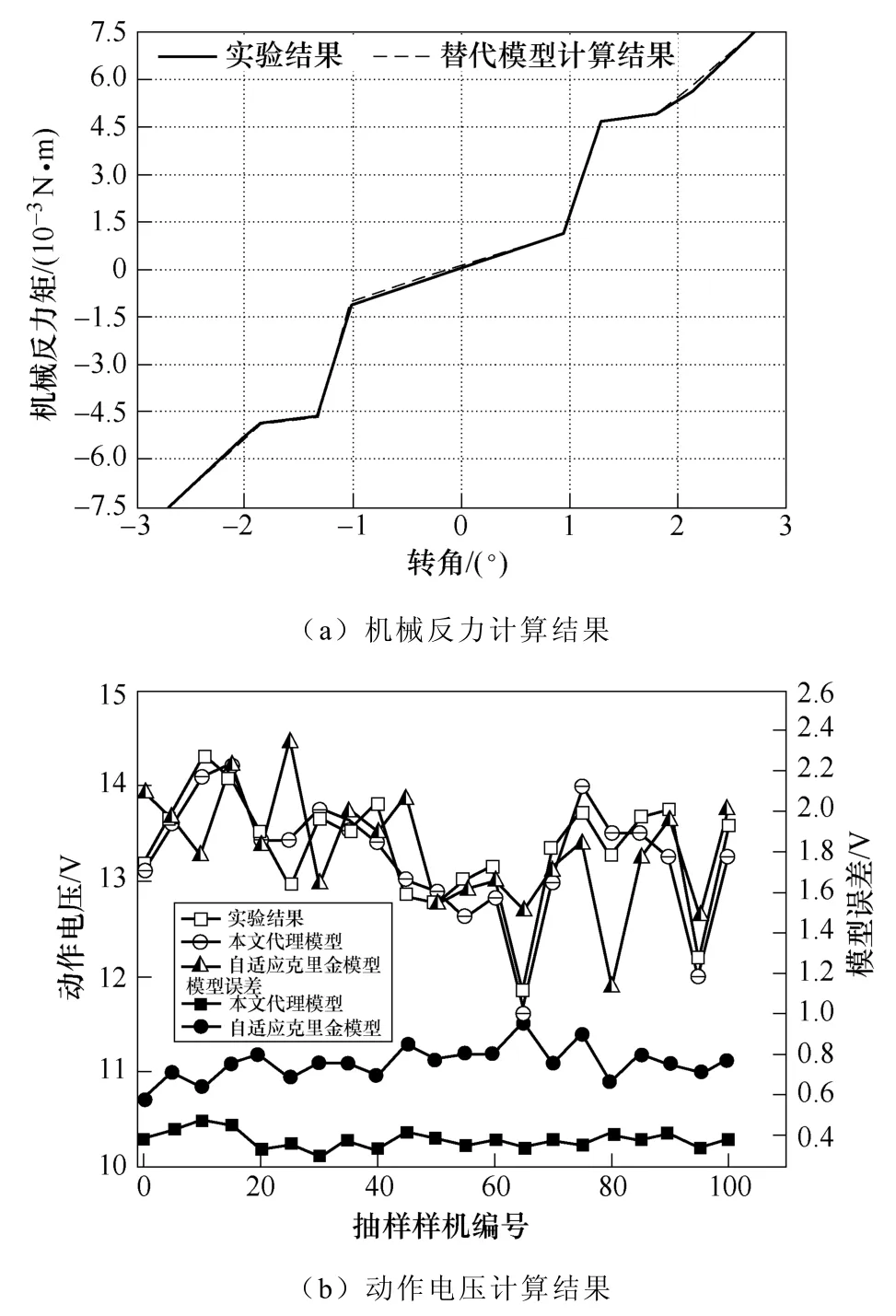
图7 MLAER 性能参数计算结果对比Fig.7 The comparison of performance parameters results for MLAER

可见，本文所提方法建立的MLAER 静动态性能特征代理模型最大计算误差仅为6.72 %，与虚拟样机模型的计算精度较为接近，但代理模型训练完成后单个样本的计算时间为176 s，计算速度与精度可满足MLAER 性能提升与一致性设计要求。

结合电磁继电器性能提升与本文研究对象的型谱设计要求，主要优化目标如下：

（4）分断动能Ebreak同样是望大特征。

（5）0 V 电磁吸力曲线形态系数δ越小越好，为了提升优化效率，本文将望小特征转化为望大特征e-δ。

同理，由电磁继电器性能提升方法可知，该继电器的主要涉及参数有：衔铁长度、衔铁厚度、轭铁长度、轭铁厚度、永磁体长度、永磁体宽度、永磁体厚度、永磁体与轭铁上极面距离、动簧片厚度、动簧片宽度、动簧片长度、触点间隙、触点超程、触点自由程、触点初压力、永磁体剩磁、磁间隙。

针对该继电器质量提升与一致性设计需求，在设计参数允许范围内，使用改进的自适应种群多目标差分进化算法进行寻优，优化前后设计参数对比见表3。

表3 优化前后设计参数对比Tab.3 The comparison of design parameters before and after optimization

优化结果的静动态性能特征（衔铁保持力、衔铁是否中位、动作电压、静合触点分断速度和动合触点分断速度）均值和优化前对比结果见表4。

表4 优化前后性能特征对比Tab.4 The comparison of performance characteristics before and after optimization

可见，该继电器的性能参数在优化后实现了整体提升，其中静合触点分断速度提升高达16.8 %（由28.7 mm/s 提升至33.52 mm/s），提升幅度最小的动合分断速度也达到了10.2 %，且无中位现象。

为了验证该继电器批次产品质量一致性的提升情况，在设计参数容差范围内使用蒙特卡洛生成虚拟样本2 000 台，以动作电压为例计算性能参数质量一致性的提升幅度，统计结果如图8 所示。

图8 MLAER 动作电压一致性提升对比Fig.8 The comparison of MLAER operation voltage consistency improvement

可见，本文所提优化方案在显著降低批次产品动作电压均值的同时将动作电压的质量一致性提升了 40 %（将动作电压标准差由原始设计的 0.65 V降低至0.39 V）。

在联合研发厂家的支持下，使用优化方案制作实物样机100 台，并使用图9 所示的继电器综合参数测试和耐力学试验系统，对100 台物理样机进行参数测试。测试表明优化后产品无衔铁中位，耐力学性能满足 10～3 000 Hz 30 g、动作电压不高于13 V 的要求，同时统计分析动作电压分布情况，统计分析结果如图10 所示。

图9 MLARE 性能特征试验平台Fig.9 Platform for testing the performance characteristics of MLARE

图10 MLAER 动作电压分布情况Fig.10 Distribution of operation voltage of batch manufactured physical prototypes of MLARE

可见，批次制造继电器的动作电压一致性较好，方差为0.33 V，甚至优于批次虚拟样机的模拟结果，显著改善了继电器性能特征一致性不佳的情况。

3 结论

本文针对有限元忽略非线性各向异性永磁体充退磁效应导致的计算效率低精度差，忽略了设计参数与性能参数之间的作用机理造成的寻优效率较低等问题，开展了体系化研究，取得了以下成果：

1）提出一种可适用于各类继电器虚拟样机建模方法，即基于S-W 模型计算非线性各向异性永磁体充退磁后的磁偶极子的矢量化信息，进而使用Preisach 模型得到永磁体局部磁滞曲线，在此基础上建立继电器静动态性能特征虚拟样机模型，计算得到继电器的静动态特征，并将计算结果与实测结果进行比较，最大误差为5.01 %，分析与计算精度较高，可以满足本文的优化需求。

2）针对虚拟样机计算效率低，现有代理模型计算强高维强非线性、存在过零特征性能计算精度差的问题，提出一种适用性强、可用于各类继电器的快速建模与计算方法，即在少量虚拟样机模型计算值的基础上，基于模糊混沌展开建模代理模型基函数，使用径向基函数方法建立修正实测结果与计算结果之间偏差的误差补偿函数，基函数和误差补偿函数共同构成本文代理模型。将继电器代理模型计算结果与实测结果进行对比，最大误差为6.72 %，计算精度与虚拟样机相近，计算用时不到虚拟样机模型的1 %（由5 h 降低至176 s）。

3）在代理模型的基础上，从吸反力配合和分断动能等角度出发，确定继电器性能特征形成机制和改进方向，同时为了满足多目标寻优的需求，改进多目标差分进化算法，提出自适应种群进化策略和基于小生境思想的最优解集筛选策略，可以更均匀更快速地得到最优Pareto 前沿解集组合，一定程度上可以避免迭代寻优过程早熟和陷入局部最优解集，增强解分布的广泛性和均匀性，保证MLAER多相关性能参数的迭代优化精度和效率。

4）以双磁钢差动式MLAER 为验证对象，对其衔铁中位、动作电压超差等潜在归零故障进行优化设计，给出了设计参数的最佳中心值和容差组合，在解决该继电器潜在归零故障的同时将其质量一致性提升了40 %。优化结果验证了考虑非线性永磁体充退磁效应的虚拟样机模型、引入实测结果的代理模型以及自适应种群策略的差分进化算法等方法的有效性。