基于数据挖掘的教学信息分析技术研究
2023-03-02贺娇娇严武军刘守业
贺娇娇,严武军*,刘守业
(太原师范学院 计算机科学与技术学院,山西 晋中030619)
0 引言
近年来,高校教育与就业市场的职业需求不匹配日趋严峻,根据OBE教育理念(成果导向教育),高校开始分析学生的信息以找到适合学生的教育方法,随着信息技术的不断发展,教学信息分析技术越来越受到关注,它可以帮助教师更好地了解学生的学习情况和学习习惯,提高教学效率和质量.
由于大规模数据集的产生,加之传统关联规则算法Apriori算法的不足,为此提出了控制Apriori算法中前后项集的生成,解决了AR结构约束问题,极大地提高了挖掘兴趣和高价值关联规则的效率,再将优化的Apriori算法(FR-Apriori)和MapReduce结合对教学信息中的数据进行挖掘,可以加速数据处理,提高数据分析的效率.
1 研究现状
1993年,Agrawal等首次提出了挖掘客户交易数据库中项集之间的关联规则问题;2014年Zheng X,Wang S[1]在Apriori算法的基础上提出了一种基于剪枝Eclat算法和MapReduce的道路运输管理信息挖掘方法研究;2019年赵欣灿[2]、朱云、毛伊敏针对Apriori算法效率低下等问题,提出了一种WDU的动态加权增量挖掘算法,构建了CTP方法,解决了项集扫描次数多的问题;2020年Su F,Yuan Q[3]等将Apriori[4]算法用于道路交通事故,挖掘出事故结果的与事故客观因素的关联;2021年徐胜超[5]、宋娟、潘欢提出基于MapReduce并行关联挖掘的网络入侵检测的Cloud-Apriori优化算法,证明了新Cloud-Apriori优化算法相比于已存在的网络入侵算法而言,确实更具优势;2022年,吕立新和杨帆[6]同样针对Apriori算法效率低等问题,提出并设计了基于W-DPC策略的改进Apriori算法,为社会各领域信息分析提供了有效参考.
综上所述,Apriori算法目前已应用于商业、道路等多个领域,并取得了良好的效果.然而,将Apriori和MapReduce结合的优化算法应用于高校教育的研究尚不多见.
2 基本算法及概念介绍
2.1 关联规则及相关概念
关联规则简单来说就是从海量数据中挖掘出项集的关联关系,最典型的就是啤酒和尿不湿事件,经调查发现67%的用户购买啤酒的时候同时也会购买尿不湿,故而商超将两者摆放在一起就可以提高销售额.大型商城都会有专门的数据分析师,通过分析各种商品之间的关联关系来了解用户的心理,并据此设计商城的营销策略.
关联规则是一个形如X⟹Y的表达式,其中X和Y是不相交的项集(譬如{啤酒,尿不湿}被称为2-项集),关联规则的支持度是对X和Y的支持度.
Support(X⟹Y)=P(X∪Y),式中是表示X出现时Y也出现的可能性(即超市同时购买啤酒和尿不湿的顾客占购物总顾客的比例).
关联规则的置信度是X出现的时候Y也出现的概率.
Confidence(X⟹Y)=P(Y|X),式中是表示发生X事件的基础上发生Y事件的概率(即超市购买啤酒和尿不湿的顾客占购买啤酒的顾客的比例).
2.2 Apriori算法
2.2.1 Apriori算法及相关概念
Apriori算法是频繁模式挖掘的一个简单而有效的算法,也是最经典的关联规则算法.该算法中最常用的几个名词就是支持度、置信度、频繁项集、候选项集.支持度和置信度在2.1中已给出.
频繁项集:假设给定的最小支持度阈值minSupport,如果有support(C)>minSupport,则称该集合为频繁项集.
候选项集:假设给定频繁项集Ck(k∈1,2,…,n),其中Ck[i]和Ck[j]中有k-1个属性值相同且唯一不同地分布在Ck[i]和Ck[j]中,则通过两两连接可得出候选集.
2.2.2 Apriori算法的基本思想
(1)频繁项集的生成.传统Apriori算法采用逐层搜索的模式,通过用户给出的最小支持度求出所有频繁项集,即所有支持度不小于最小支持度的项集.这些频繁的项集可能具有包含关系.通常只关心那些不被其他频繁项集包含的所谓频繁大项集,而这些频繁大项集是形成关联规则的基础.
(2)生成关联规则.利用用户给出的最小置信度,在每个最大频繁项集中找到置信度不小于最小置信度的关联规则.关联规则挖掘的整体性能取决于频繁项集的生成,生成关联规则相对容易.
该算法首先输入事务数据库、minSupport,k=1;扫描整个数据集,假设候选频繁0-项集为空集,搜索候选频繁1-项集及相应的支持度,通过剪枝去除低于支持度的1-项集,得到频繁的1-项集.然后连接剩余的频繁1-项集得到候选频繁2-项集,过滤掉低于支持度的候选频繁2-项集,得到频繁2-项集,如此反复.直到找不到频繁的k+1个项目集,也就是Lk为空对应的频繁的k个项目集就是算法的输出结果.Apriori算法流程图如图1所示.
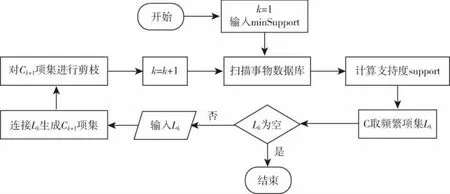
图1 Apriori算法流程图
2.2.3 优化Apriori算法(FR-Apriori)
随着数据量的增长,Apriori算法的执行也受到一定的限制.为了提高效率,进行了如下优化:
通过划分数据块和控制前后项集(F表示前项集,R表示后项集)生成,解决了AR结构约束问题,极大地提高了挖掘兴趣和高价值关联规则的效率.它确保每个规则以预期的形式呈现给用户,同时避免无效的关联规则.
1.FR-Apriori算法基本概念
1)项i是项I的主要组成部分.I由前项If和后项Ir组成.对于教学信息分析,If表示诱发因素,如学生自身学习能力和教师自身能力等分类触发因素,Ir表示最终状态事件,如优秀状态和非优秀状态.
2)项目I是一个项目集合,定义为:I=If∪Ir={I1,I2,…,In}式中If为前项集,If=If1,If2,…,Ifn.Ir是后项集,其中Ir={Ir1,Ir2,…,Irn}.If与Ir无交集,即If∩Ir=.
3)事务数据库T由具有唯一事务标识TIDs的事务组成,其中T={t1,t2,…,tn}≠.每个事务t对应于T的一个子集,至少包含一个前项和一个后项.

5)先验集Xf是If的所有非空真子集的和,其中Xf={X1,X2,…,Xn}.例如,如果If={A1,A2,A3,B1,B2},则其非空固有子集包括{A1,B1},{A2,B1},{A3,B1},{A1,B2},{A2,B2} 和 {A3,B2}.因此,
Xf={{A1,B1},{A2,B1},{A3,B1},{A1,B2},{A2,B2},{A3,B2}}
6)结果集Yr是所有事务中Ir的所有非空真子集Yr={Y1,Y2,…,Yn}的和.例如,对于Ir={C1,C2,C3},非空的固有子集是{C1},{C2}和{C3}.
7)潜在信息集V由Xf和Yr组成,是Xf和Yr的笛卡尔积
8)支持度是指同时包含X和Y的事务数与数据库中事务总数的比值.定义如下:
式中Count(X∪Y)是同时包含X和Y的事务数.|T|是事务总数.
9)置信度表示假设X发生,Y发生的概率.定义如下:
式中Count(X)是包含X的事务数.
10)强关联规则(SAR)是满足用户指定的评价指标的候选关联规则,即最小支持阈值(即Min_Supp1和Min_Supp2)和最小置信阈值(Min_Conf).
2.MapReduce基本概念
MapReduce是一个由MRAppMaster、MapTask、ReduceTask构成的分布式程序的通用框架,解决分布式计算中的复杂性.最初是由Google提出,用来解决搜索引擎中大规模网页数据的并行化处理问题.目前MapReduce主要用来解决海量数据的计算问题.
MR由两个阶段组成:Map(映射)和Reduce(规约),在运行上采用一种“分而治之,先分后合”的思想.目前使用广泛一方面原因是它的计算简单,用户只需要根据业务逻辑编写Map()和Reduce()两个函数,其余的系统层面的细节,诸如数据存储的划分、分发等均由框架来完成.
MR的工作流程:Map阶段、shuffle阶段、Reduce阶段.
①在Map(映射)阶段读取大规模数据集的内容并将要处理数据进行逻辑切片(split),将split后的数据子块解析为key、value对.
②并行运行多个Map任务,MapTask(映射任务)由程序员根据相应的业务逻辑编写,对输入的键值对进行处理并写入其内存缓冲区.
③写入内存缓冲区的数据量达到其设置的阈值后会进行spill(溢出)并根据key进行sort(排序),再sort的基础上进行combiner(聚合),以减少网络带宽的开销,将相同key对应的value提取出来进行分组输出给shuffle.
④经过shuffle(混洗)阶段得到Map阶段处理后的数据
⑤Reduce阶段按照key的value列表进行全局的汇总处理,最后,把Reduce的输出结果保存到HDFS上.如图2是MapReduce处理数据集的过程图.

图2 MapReduce处理数据集的过程图
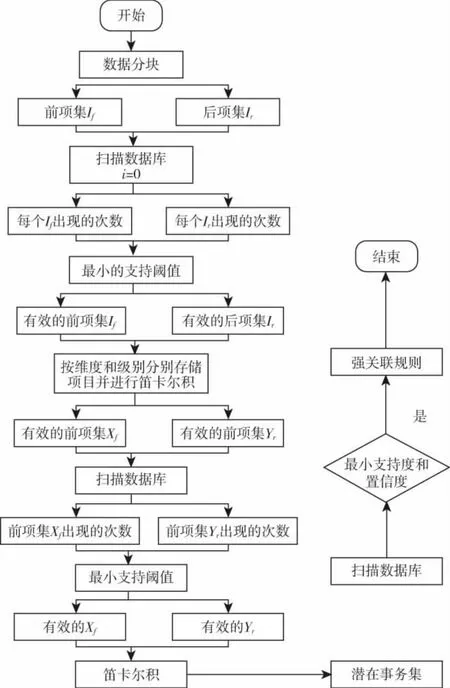
图3 基于MapReduce的FR-Apriori算法流程图
3.计算过程
基于MapReduce的FR-Apriori算法计算过程:
1)根据最终所要达到的目标,首先将事务数据库横向划分为n个大小近似相等的数据子块,然后将划分的数据字块发送给m个节点.m远小于n,这里采用随机分区策略[7].在m个节点上分别推断其所获得的关联规则的前后项.最后,将获得的所有前项和后项分别存储在前项集If和后项集Ir中.
2)扫描数据集,统计If和Ir中所有项目的出现次数.用Map集合进行存储并排序.
3)根据上一节中描述的第一个最小支持阈值Min_Supp1,过滤掉If和Ir中的部分项.然后在上一步的Map集合中,找到有效前项集If和有效后项集Ir并按不同维度和层次存储符合条件的项目.
4)通过If和Ir中存储的项目不同维数之间的笛卡尔积的迭代计算,得到潜在的前、后最大频繁项目,分别存储在前集Xf和后集Yr中.其中,充分考虑了不同因素之间的排列关系对Xf的笛卡尔积结果的影响.
5)通过T的第二次扫描,计算出Xf和Yr中所有最大频繁项的出现次数.
6)根据Min_Supp1,对Xf和Yr中的所有最大频繁项进行过滤.符合条件的项目存储在有效前项集Xf和有效后项集Yr中.
7)计算Xf与Yr之间的笛卡尔积,将所有组合的项目集放入潜在交易集V中.通过对T的第三次扫描,计算出V中所有非空固有子集的出现次数.
8)根据第二最小支持阈值Min_Supp2和最小置信阈值Min_Conf对V中的非空固有子集进行滤波,直至计算结果均为非频繁项集,汇总前面所有的频繁项集.
从上面的过程可以看出,改进后基于MapReduce的FR-Apriori优化算法有三个优点:第一,通过对前后项集的过滤可以有效减少数据集的规模;第二,它只需要读取数据库D三次就可以挖掘所有的频繁项集,这减少了算法在运行中的资源开销,它可以不受干扰地在每个节点上进行局部频繁项集的发现.该设计既能满足并行计算的要求,又能减少节点间数据传输带来的网络通信开销;第三:引入MapReduce并行化处理进一步提高了算法的性能.
3 实验结果与分析
为了验证所提方法的有效性和性能,总共使用6台计算机,其中1台计算机作为master节点,剩余5台作为slaver节点,处理器均为英特尔酷睿i7处理器,时钟速率2.10 GHz,内存8.00 GB,使用IntelliJ IDEA 2020.3.2进行编程.实验数据集来源于信息不对称情况下太原师范学院2021届计算机科学与技术学院的学生信息.该方法旨在使管理者了解到OBE理念下学生信息之间的关联规则,从而制定合适的教学目标.因此,本文只描述和比较了该方法的性能,不重复关联规则的挖掘结果.
为检验经过优化后的算法的有效性和实用性,首先设置一个最小支持度为5%,图4和图5分别显示了改进后的FR-Apriori算法和改进前的Apriori算法在5种不同约束下的规则数,以及FR-Apriori算法和Apriori算法进行实施的持续时间.

图4 FR-Apriori和Apriori在5种不同约束下获取的规则数
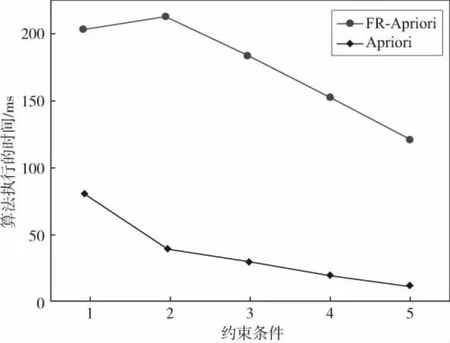
图5 FR-Apriori和Apriori在5种不同约束下算法的执行时间
从上图中可得出,FR-Apriori算法与Apriori算法相比,获取的规则很少,说明FR-Apriori剪枝程度远远大于Apriori算法,在执行时间上也远远大于经典Apriori算法,具有较高的挖掘效率,论证了FR-Apriori算法的有效性.
在基于上一个试验的基础上,接着验证基于MapReduce的FR-Apriori算法的性能,即在集群环境下FR-Apriori算法的性能.选取太原师范学院2021届计算机科学与技术学院的学生信息的20%、40%、60%,设置最小支持度为5%,10%.试验结果如图6、图7所示.说明了算法执行时间随着计算节点的增多而减少,且同样的数据在不同的支持度下也呈现不同的趋势,支持度越大,执行时间也越短,算法的优势也就越明显.
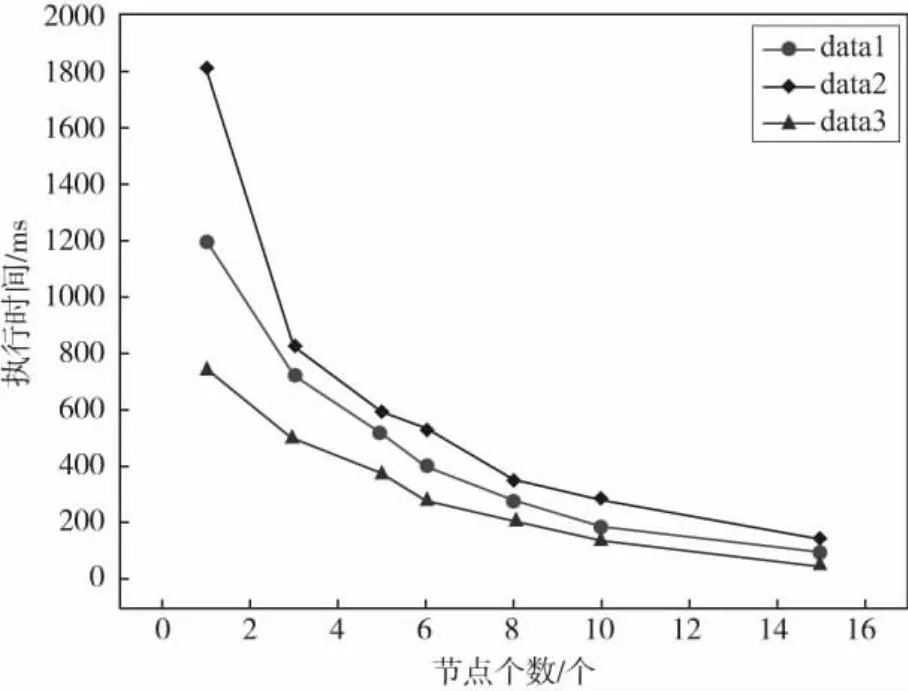
图6 支持度为5%的执行时间对比
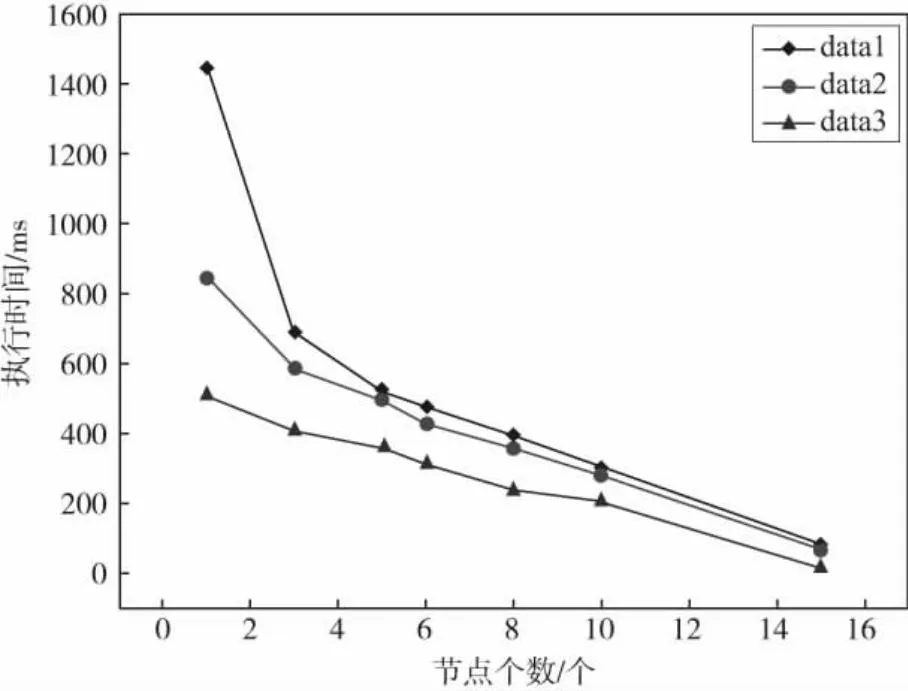
图7 支持度为10%的执行时间对比
4 结论
关联规则在高校教育的最新应用研究集中在时空数据挖掘上.这些结果应用于数据本身具有明显的时间序列属性,而教学信息的无序多为非结构化数据,利用其规律性规则更加困难.由于教学信息受到高校老师和管理者的影响,具有多个相关数据,因此探索新的关联规则挖掘方法也有用于教学管理信息数据.本文针对Apriori算法的不足,提出并论证了以课程为前缀或后缀的候选集可以对这两种属性进行剪枝计算;结合MapReduce函数设计的Map和Reduce函数的特点,提出了一种综合优化方法.最后,通过试验结果证明了该算法的性能优势.
