针对多类恐怖袭击的机场资源配置问题的松弛算法

2023-03-02逯婧瑜闫喜红郭思怡

太原师范学院学报(自然科学版) 2023年4期

逯婧瑜,闫喜红,b*,郭思怡

(太原师范学院 a.数学与统计学院;b.智能优化计算与区块链技术山西省重点实验室,山西晋中 030619)

0 引言

近年来,我国的民航事业,包括航空企业的旅客运输量和机场建设方面,都取得了很大的进步.到2020年年底,我国国内已经颁证的民用航空机场共241个,如何保护如此庞大的国内机场网络[1]是一项具有挑战性的任务.

目前,国内外针对机场安全的研究有很多.比如,对机场安全风险评估中存在的问题继续进行优化设计[2];对机场安全运行机制进行分析[3];对机场净空障碍物进行分析测量[4];对多目标的机场停机位的预警分配模型的构建[5]等.但是针对国内机场网络的整体安全保护的研究较少,Yan等[6]针对同一类型的恐怖分子袭击国内机场网络资源配置问题,建立了双层优化模型,其中上层模型为政府向各机场提供预算分配,下层模型是恐怖分子选择一个航班进行攻击,从而使预期损失最大化,并采用了割平面算法来求解此双层优化问题,同时进行了敏感性分析.

为了提高国内机场网络安全性,在Yan等[6]的研究基础上,考虑到实际情况中恐怖分子类型多种多样,不同能力的恐怖分子通过机场的概率不同,从而建立针对多种类型恐怖分子的保护国内机场网络安全的预算分配模型,并采用松弛割平面算法来求解该模型.

1 问题描述及模型建立

以下将研究如何有效地将资源分配给国内机场,以保障整个机场网络.事先政府会确定分配给每个机场的预算数额,并估计恐怖分子成功通过各个机场的概率,从而提出一个双层优化模型[6],其中政府是领导者,恐怖分子是追随者.恐怖分子会通过情报获取其成功通过率等信息,在预算有限的情况下,决定采取选用哪类方式对哪些航班段进行攻击.恐怖分子的目标是将预期损失最大化,而政府的目标是将恐怖分子造成的最大预期损失最小化.参数设置如下表1.

表1 问题模型符号列表

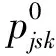
下面定义决策变量:

设x,y分别是xi,yjljk对应的向量和矩阵,根据上述引入的参数和决策变量,建立如下双层优化模型:

(1)

(2)

(3)

yjljk∈{0,1}, ∀j∈J,k∈K,lj∈{1,…,nj},

(4)

在上层优化中,政府希望在预防恐怖分子袭击事件时使得预计产生的损失W减少到最小.集合X可以保证国内所有机场获得的政府分配的预算值总数在政府计划限额BG之内,同时也可以保证具体到每一个机场的预算分配也在相应规定的范围内.在下层优化中,恐怖分子也希望能通过制定最佳的攻击方案从而将可能造成的破坏提升到最大.约束条件(2)保证了恐怖分子只能选择一趟航班中的其中一个航班段进行攻击.约束条件(3)保证了恐怖分子预设的攻击成本在其合理的计划限额BT之内的.

2 松弛割平面算法

对于上述双层优化模型,采用松弛割平面算法.松弛割平面算法是目前针对大规模0-1整数规划问题的一种有效求解算法[7].相比于割平面算法可以使大规模问题在很短的时间内得到一个较好的解.

该算法流程如下:

松弛割平面算法

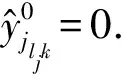
(5)

(6)

(7)

Li≤xi≤Ui, ∀i∈I.

(8)

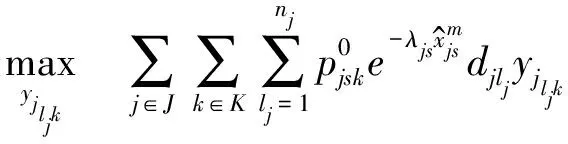
(9)

(10)

(11)

yjljk∈[0,1], ∀j∈J,k∈K,lj∈{1,…,nj}.

(12)

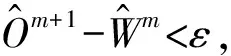
3 数值实验

为了验证所提出算法的有效性,将利用松弛割平面算法做了大量数值实验,如下表2.所有的算法用MATLAB(R2019b)编写.下面考虑10个机场所构成的机场网络.取政府的总预算均为20万元,恐怖分子的总预算为50万元,雇佣第1类恐怖分子费用为20万元,雇佣第2类恐怖分子类型为30万元,其余数值随机生成.通过将航班数从50增加到240,验证了算法的有效性.不同规模问题的实验结果表明,所提出的松弛割平面算法能在合理的时间内取得较为满意的可行解.