无里程计移动机器人多传感器融合定位算法*

张礼睿，孙勇智，刘力铭，李津蓉，许 垚

(浙江科技学院自动化与电气工程学院，杭州 310023)

0 引言

稳定精确的定位结果是实现移动机器人在未知环境自主移动的首要条件。移动机器人的定位是指在运动过程中，机器人通过搭载的传感器感知周围环境并采集运动数据，确定自身的位置信息[1]。根据移动机器人定位过程，主要分为绝对定位和相对定位[2]。目前，移动机器人定位最常用的方案是使用轮式里程计和惯性测量单元(inertial measurement unit，IMU)测量机器人的运动数据，使用激光雷达传感器或视觉传感器测量周围的障碍物信息，通过多传感器数据融合算法完成室内定位和导航[3]。

然而在实际生产生活中，部分移动机器人因为机械结构的限制、工作环境或成本因素无法安装轮式里程计[4-5]，从而影响机器人的定位。为解决这个问题，IBRAGIMOV、龚学锐等[6-7]提出使用视觉里程计代替轮式里程计，通过VIORB-SLAM、DPPTAM等图像处理算法，从摄像头采集的图像中得到机器人的线速度、角速度等数据，从而完成室内定位任务。但视觉传感器对CPU计算能力要求高、算法复杂且实现成本高，并不适合在低成本的移动机器人系统上安装使用。除了使用视觉里程计代替轮式里程计，严小意等[8]提出了激光雷达和IMU相融合的导航定位系统，使用激光雷达提取环境特征和构建地图，通过IMU采集姿态信息进行卡尔曼滤波，补偿位置和姿态输出的误差。但IMU中的加速度传感器测量噪声大[9]，导致机器人运动数据并不准确。胡钊政等[10]提出基于卡尔曼滤波框架的WiFi、激光雷达与地图的融合定位新方法，利用卡尔曼滤波器实现机器人高精度的融合定位。但机器人定位问题本质上是非线性系统状态估计问题[11]，采用卡尔曼滤波处理非线性系统问题时，会造成收敛性较差，增大误差的问题，进而影响定位精度。

RF2O(range flow-based 2D odometry)是一种基于测距流的平面运动估计算法[12]，其计算量小、精度高，可以代替轮式里程计，从激光雷达的连续范围扫描中计算出移动机器人的运动数据。因此，本文提出使用扩展卡尔曼滤波(extended kalman filter，EKF)融合RF2O算法和IMU的数据，提高系统收敛性，得到相对定位数据，再使用自适应蒙特卡洛定位算法(adaptive monte carlo localization，AMCL)进行修正，减小误差累计，实现无里程计移动机器人的精确定位。

1 扩展卡尔曼滤波

扩展卡尔曼滤波是卡尔曼滤波解决非线性系统问题的一种变种方法，其核心是将非线性系统经过线性化处理后再进行卡尔曼滤波计算[13]。

在机器人模型中，假设系统的真实状态与上一时刻的状态和当前系统输入有关，系统的测量状态与当前系统的真实状态有关，则建立系统的状态转换模型和传感器观测模型如式(1)所示。

(1)

式中，k为离散时间；xk为在k时刻下系统的真实状态；uk为输入矩阵；wk为过程噪声，假定符合w(k)～N(0,Qk)的多元高斯噪声；zk为在k时刻下的测量；vk为测量噪声，假定符合v(k)～N(0,Rk)的多元高斯噪声；f(x,u)、h(x)分别为非线性可微的状态转换函数和测量函数。

基于上述模型，将扩展卡尔曼滤波求解分为状态预测和测量更新两个方面。

(2)

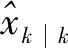
(3)

2 基于EKF的融合算法

进行移动机器人的定位首先需要获得机器人的速度、加速度和角速度等数据。激光雷达可以感知机器人周围的环境，通过发射激光信号获取目标距离和速度等数据。IMU可以测量出机器人的角速度和加速度数据，但IMU中的加速度数据噪声大，导致推算出的机器人速度数据误差很大，从而影响机器人的定位。

为解决该问题，本文采用融合RF2O算法和IMU数据的方案。RF2O算法能够估计激光雷达的平面运动，计算出机器人的运动数据。激光雷达的速度约束方程[12]如式(4)所示。

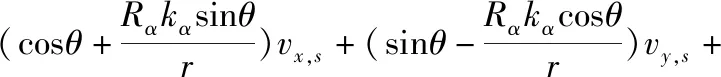
(4)

式中，r和θ为激光扫描点与雷达之间的距离和夹角；Rα和Rt为r对夹角θ和时间的偏导；x和vx,s、y和vy,s以及ωs为移动机器人的运动数据，即X、Y轴上的速度与位移以及机器人的角速度；kα为常数，与激光雷达的性能有关。

式(4)推导过程中假设周围环境静止，并且舍去了泰勒展开后的高次项，同时激光雷达在旋转时还会产生角度误差，导致计算出的角速度数据并不准确，所以需要在此基础之上融合IMU的数据以得到精准的结果。

本文的机器人系统仅考虑平面上的运动，即X、Y轴上的平移运动与Z轴上的旋转运动。根据EKF的设计原理，建立系统状态转换模型如式(5)所示。

(5)

式中，Xk、Yk和θt分别为移动机器人在X、Y轴的位移以及偏航角；vk、φk和ωk分别为X、Y轴的线速度和角速度[14]。

融合RF2O算法计算的机器人X、Y轴线速度和IMU测量的机器人角速度，建立传感器观测模型如式(6)所示。

(6)

在机器人系统运行的过程中，传感器每次测量得到数据后，通过扩展卡尔曼滤波的预测式(2)和更新式(3)的不断迭代，逐渐估计机器人系统的状态。

3 AMCL算法修正

扩展卡尔曼滤波本质上是对速度和角速度进行积分运算得到机器人的位移和偏航角数据，因此随着系统运行时间的增加，误差累计也会随之增加，进而影响机器人的定位结果。

自适应蒙特卡洛定位算法是一种估计机器人在地图中的姿态的定位方法[15]。该算法通过产生随机粒子来估计机器人的位姿状态，每个粒子都代表机器人未来可能的状态。在机器人运动过程中，AMCL算法会逐渐丢弃与观测不符的粒子，保留并重新生成更多与观测一致的粒子，最终粒子会不断收敛至机器人实际所在位置，从而完成机器人的定位任务[16]。使用AMCL算法计算得到定位数据是机器人以地图数据为参考的定位，因此没有误差累计的问题。但AMCL算法会遇到绑架问题[17]，即当机器人丢失了先前的位置信息或者得到了一个错误的位姿信息，机器人就无法依靠AMCL算法继续计算当前的位置信息。

为解决该问题，本文提出扩展卡尔曼滤波和AMCL算法相结合的方案，即使用扩展卡尔曼滤波计算出机器人的定位数据后，再使用AMCL算法测量该定位数据的累计误差得到修正值，最后使用扩展卡尔曼滤波的计算结果减去修正值，得到精度更高且没有误差累计问题的定位数据。

扩展卡尔曼滤波可以减少误差累计对系统的影响，从而解决AMCL算法的绑架问题。由于AMCL算法仅起到修正累积误差的作用，而累计误差在短时间内变化较小，因此修正值的更新频率可以远远低于扩展卡尔曼滤波算法，以此来减少定位系统的总体计算量。最终定位系统的传感器数据处理框图如图1所示。

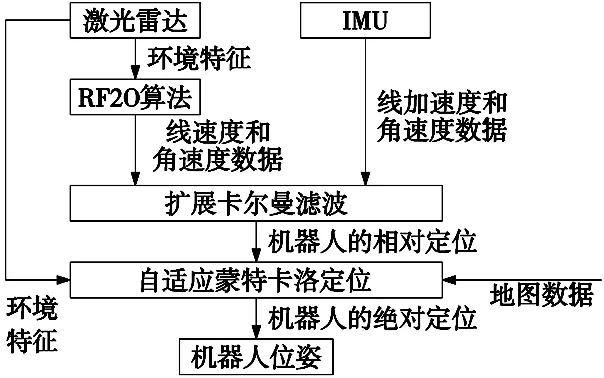
图1 传感器数据处理方案框图

该方案只需要使用IMU和激光雷达传感器。RF2O算法通过激光雷达数据计算得到机器人的线速度，IMU通过测量得到角速度，再经过扩展卡尔曼滤波融合得到相对定位数据。最后，为克服相对定位数据的误差累计问题以及在该数据的基础上进一步减少测量误差，使用AMCL算法来修正机器人的相对定位，得到绝对定位数据。通过相对定位可以得到准确并且连续的机器人线速度、角速度和加速度数据，通过绝对定位则可以得到比较准确且没有误差累计的机器人位移、偏航角数据。

4 实验与结果分析

4.1 Gazebo仿真实验

为了定量比较不同定位方案的效果，本文在Gazebo软件中进行仿真实验。在IMU和激光雷达的测量上增加高斯噪声，以更加贴近真实场景。在仿真环境下控制模拟机器人移动，记录不同定位方案的计算结果并与真实值做比较。

本文采用均方根误差(RMSE)来描述测量的误差[18]。假设P1,…,Pn为预测的姿态数据序列；Q1,…,Qn为真实的姿态数据序列；Δ为每秒的数据间隔，即每秒钟预测的姿态数据个数，本次实验Δ=10。均方根误差的计算表达式为：

(7)

仿真实验中采集移动机器人的定位数据，计算得到的不同定位方案的均方根误差，并记录不同定位方案的最大测量偏差，如图2和图3所示。

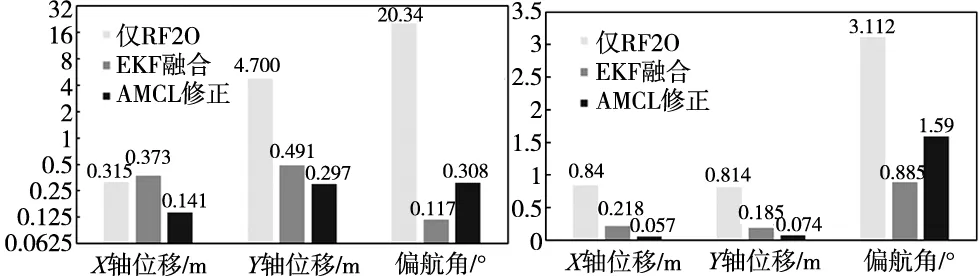
图2 不同定位方案的均方根误差 图3 不同定位方案的最大测量偏差

分析图中数据可知，经过AMCL算法修正后的定位方案相比EKF融合方案，X轴和Y轴位移的均方根误差分别下降了62.1%和39.5%，最大测量偏差不超过0.074 m。由于使用IMU测量得到机器人角速度数据，使得经过EKF融合后的偏航角误差较小，引入AMCL算法反而增大了偏航角的测量误差，但该误差仍然较小，最大测量偏差不超过1.6°。

4.2 移动机器人定位实验

为了验证仿真实验中得到的结果，本文使用真实的机器人在现实环境中完成定位任务。机器人平台如图4a所示，硬件采用阿克曼车型的底盘，下位机使用KEA128单片机主板控制机器人运动，同时装载一台LS01G型激光雷达和ART-IMU-02A型IMU，上位机为一台CPU为i3的工控机，配有Ubuntu16.04以及Kinect版本的ROS操作系统。

在现实环境中由于无法测量出定位数据的真实值，也就无法对测量结果进行定量比较。因此，本节通过定位数据以及激光雷达测量的障碍物数据绘制地图来定性地比较不同定位方案的性能，用于实验的环境如图4b所示，包含走廊和房间。

(a) 移动机器人平台 (b) 实际环境图4 实际环境定位实验

远程控制机器人在走廊上移动，不同定位方案得到的机器人运动轨迹以及建立的地图如图5所示。其中，图5a为参考建图，定位数据是由目前普遍使用的基于粒子滤波的SLAM算法融合RF2O算法结果和IMU数据产生，图5b的定位数据全部源于RF2O算法，而图5c中的定位数据则是来自于本文提出的算法方案。

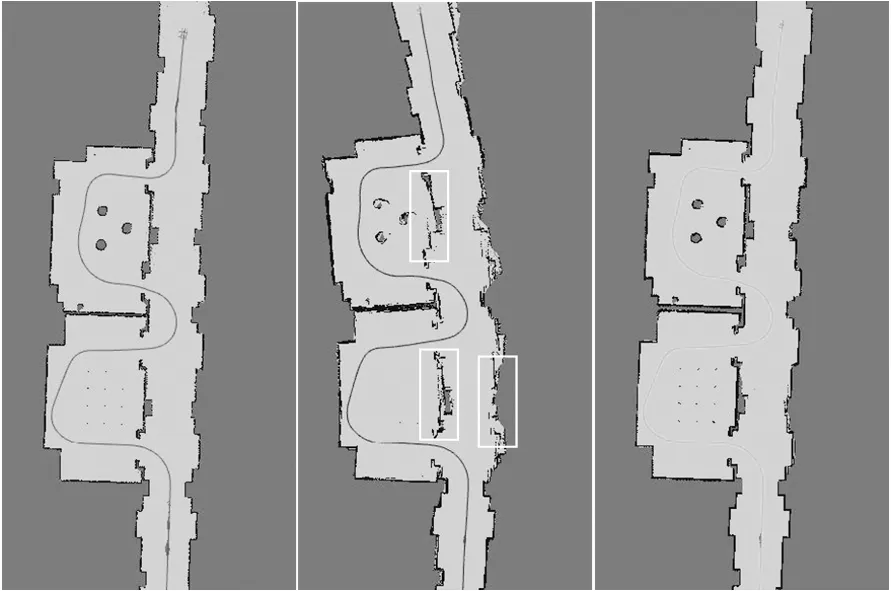
(a) 参考建图 (b) 使用RF2O算法得到定位数据建图 (c) 使用本文方案得到定位数据建图图5 不同定位方案估计轨迹以及地图对比

对比3种方案建立的地图效果可知，仅使用RF2O算法计算得到的定位数据误差最大，图5b方框中的地图边缘模糊，出现明显形变，这是RF2O算法计算得到的角速度误差较大导致的。而图5c使用本文提出的算法方案，最终建立的地图边缘清晰、距离估计准确，非常接近参考地图，证明定位数据误差较小。

表1为不同算法方案的运行时长。对比发现，本文提出的算法计算量远远小于基于粒子滤波的参考定位方案。算法运行初期，方案平均耗时为0.068 s。随着AMCL算法逐渐收敛，方案的计算量逐渐减小，在系统运行10 s后，方案平均耗时逐渐稳定，仅为0.025 s。

表1 不同算法方案运行时长 (s)

5 结论

本文针对无里程计移动机器人的定位问题，提出一种多传感器融合定位算法，通过EKF融合IMU数据和RF2O算法计算出的机器人线速度和角速度，得到相对定位数据；使用AMCL算法修正机器人的相对定位数据，得到绝对定位数据，从而完成移动机器人的定位任务。实验结果表明，本文提出的定位算法得到的定位数据误差较小，具有定位精度高且计算量小的优点，由于不依赖里程计数据，所以能够避免轮式里程计因轮子打滑、长时间运行误差累积而导致定位失败的问题，实现在无里程计的情况下完成精确定位。

本文目前提出的定位算法依赖激光雷达传感器，在动态场景下RF2O算法计算的机器人速度数据仍然会有较大误差，因此下一步计划引入人工路标，进行信息的深度融合，以辅助移动机器人进行定位与导航。