基于模糊博弈视角的企业联盟“双循环”合作对策研究

李 翠

(西安财经大学 信息学院,陕西 西安 710100)

0 引言

伴随市场竞争的日益激烈，尤其在“双循环”背景下，单个企业已无法适应复杂多变的经济市场，所以，企业间通过组建联盟加以应对，收益分配便成为各合作者最为关注的问题，合作博弈及其博弈解正是解决这种合作行为及收益分配的有力工具[1-3]。然而，企业在合作中组建联盟时呈现的合作格局日趋增多，尤其在“双循环”背景下，各合作企业在博弈过程中表现出的模糊特性比以往更强烈，为满足“双循环”高质量发展需求，构建可持续的稳定的合作格局及广义再分配方案是亟待解决的热点问题。

经典博弈中要么完全合作要么完全不合作的思想已不再适应“双循环”下不确定性合作情景，企业需要不同程度地与多个联盟进行合作，同时通过保留部分收益用于再发展，广义模糊联盟博弈更适合用来解决“双循环”下联盟合作及再分配问题[4-9]。尽管国内外很多学者已提出了丰富的关于模糊博弈及相关解集的研究成果[10-15]，然而，面临具有显著不确定性的“双循环”大背景，迫切需要多元化地开展系统研究。

企业联盟在“双循环”背景下因合作形成的模糊博弈其实就是各企业相互谈判的过程诠释，而在谈判过程中凝结而成的谈判集作为重要的博弈解可弥补核心等其它博弈解为空集而无法觉得最优分配的弊端[16-20]。在此基础上，本文提出广义模糊超量博弈模型，并对广义模糊谈判集进行刻画，针对企业联盟模糊凸合作博弈的广义模糊核心及谈判集解，从最大广义模糊超量均衡视角，就两解集等价性进行再论证，算例分析显示研究结论在“双循环”背景下可为企业联盟提供最优再分配方案，既满足合作者以部分资源同时与多个联盟合作的需求，又可借助保留部分收益满足联盟再发展的应用场景。

1 广义模糊超量视角下产业小循环的企业联盟博弈模型

借助满足以下映射关系的特征函数v刻画企业联盟“双循环”模糊合作博弈，即，v:FN→R，且满足：v(eØ)=0(空性)；v(s∨t)≥v(s)+v(t) (超可加性)。映射v描述了合作者可能采取的行动，并将一个实值赋予每个企业联盟，用以刻画成员企业在合作中的获得。v揭示了合作成员模糊博弈下合作约束的顶层设计，同时也呈现了在联盟实际组建中形成的相应模糊合作博弈模型，超可加性表达了不同联盟通过合作将获得比单独行动时更多收益的主要思想。

若企业联盟模糊合作模式下形成的模糊博弈v∈FN满足性质：v(s∨t)+v(s∧t)≥v(s)+v(t)，其中，函数Gs-i:[0,1]→R,Gs-i(t)=v(s-i)│t)为凸函数，即，∀a,b,t∈[0,1],0≤α≤1有，v(s-i│αa+(1-α)b)≤αv(s-i│a)+(1-α)v(s-i│b)，则称v为模糊凸合作博弈模型。

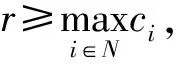
模糊博弈v∈FGN下合作联盟的广义模糊分配集I(v,r,c)即为集合[12]：

定义1针对分配向量x∈FN，企业联盟s关于x的广义模糊超量为

(1)

定义2针对分配向量x∈FN，企业联盟模糊合作博弈的特征函数若满足以下性质，则wx即为关于N上的最大广义模糊超量博弈:

(2)

企业联盟如果拥有更大的广义模糊超量值将利于促进区域产业小循环的演化，但在实际合作中可能形成多种不同的合作结构，即，对应不同的模糊合作博弈，然而，只有稳定的合作结构即博弈下才能找到全局最优再分配方案，才能实现“双循环”下持续合作格局。

2 基于广义模糊谈判集的驱动“内循环”向“外循环”演化路径

“双循环”背景下，为实现共同利益及协同效应，企业组建联盟形成模糊合作博弈，确保“内循环”与“外循环”均取得预期协同效应，才能达到“双循环”的共同利益，即，1+1>2。如果能获得全局最优广义再分配方案，即可驱动由“内循环”向“外循环”演化，实现由区域产业小循环向国际产业大循环的转型，还能满足“双循环”持续协同效应。

当企业联盟模糊合作博弈存在非空广义模糊核心解时，才拥有最优广义分配方案[13-15]，针对模糊合作博弈v∈FGN,其广义模糊核心分配C(v)即为如下集合:

(3)

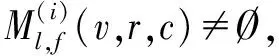
2.1 “双循环”下广义模糊谈判集的博弈过程及再分配方案

企业联盟模糊合作博弈v的一个广义分配向量用x表示，现针对分配方案x，企业k和l对其产生异议，表现为k质疑l，认为自己没有l取得的收益多，便重新组建不包含l的合作联盟s，即，在模糊联盟s∈FN中，sk>0，sl=0，y为联盟s的广义分配向量，且满足

(4a)

si·yi>si·xi,∀i∈car(s)

(4b)

其中，式(4b)中为严格大于不等式，意味着yi方案更优，(y,s)称为企业k针对l关于x的广义模糊异议。所以，企业l针对k的广义模糊异议(y,s)将会实施对应的抵制方案，企业l于是组建不包含k的模糊联盟t，生成广义分配向量z，z∈FN,zl>0,zk=0。同样，联盟t中的广义分配向量t满足

(4c)

ti·(zi-xi)≥si·(yi-xi),∀i∈car(t)∩car(s)

(4d)

ti·zi>ti·xi,∀i∈car(t)car(s)

(4e)

其中，式(4c)表明用新的广义分配方案z取代y，必须首先满足可行性，针对式(4d)当ti=1，si=1时，则对应经典意义下谈判集中的反异议中的zi≥yi，在模糊意义下之所以要拓展为ti·(zi-xi)≥si·(yi-xi)，是因为直接延拓为ti·zi≥si·yi将存在一定的局限性(比如ti很小si很大的合作情况)，而用超出的部分进行延拓将更加合理，即，ti·(zi-xi)≥si·(yi-xi)就是让超出的部分不变小，这样才能使得企业联盟“双循环”下模糊合作博弈谈判方案更具合理性。确保各合作企业在联盟t中获得的广义分配不比在联盟s中获得的广义分配少，且对于同时与联盟s和t合作的企业获得的广义分配不低于只与联盟s合作所获得的广义分配。(z,t)即为相应的广义模糊反异议。

如果对于企业联盟的一个广义模糊异议，不存在反异议，则视为该广义模糊异议是有效的。“双循环”背景下企业联盟被合作成员用于组建广义模糊异议，当且仅当它有一个正的广义模糊超量。

说明1一个联盟只有在拥有非负且其与异议联盟相交处有一个正的广义模糊超量时，才能用于组建广义模糊反异议。

基于以上分析，企业联盟的广义模糊谈判集分配方案描述如下：

令广义分配向量x为企业模糊合作博弈v的谈判点，若企业k，l代表任意两个企业，k针对l的任何广义模糊异议(y,s)都可找到l对k的广义模糊反异议(z,t)，则广义模糊谈判集即为所有谈判点x的集合，描述为:

异议都存在广义模糊反异议}

(4f)

也就是说，由于广义模糊谈判集中的任何一个广义模糊异议都有一个广义模糊反异议，所以，基于广义模糊谈判集分配方案x，企业联盟不可能拥有一个有效的广义模糊异议。

2.2 广义分配方案等价性论证

众多学者已针对传统凸合作博弈，基于凸合作博弈分配向量产生的每个超量博弈也必须为凸的角度，证明了其谈判集与核心相等[11,16-18]。现针对模糊凸合作博弈，基于最大广义模糊超量博弈均衡性研究视角，论证其广义模糊谈判集与黑犀牛的等价关系。模糊凸合作博弈广义模糊核心解的非空性证明，只需满足以下性质：(1)具有超可加性；(2)所有由广义模糊谈判集中分配向量产生的最大广义模糊超量博弈具有均衡性，即可确保“双循环”背景下企业联盟寻找最优再分配方案。

现令s*为最大模糊联盟，表明ex(s*,c)=wx(eN,c)。显然，Ø≠car(s*)≠N，且ex(s*,c)=u(s*)，同时，由于s*最大且ex为超可加的，car(t)≠Ø且car(t)∩car(s*)≠Ø，则有ex(s*,c)>ex(s*∨t,c)≥ex(s*,c)+ex(t,c)。因此，ex(t,c)<0,∀car(t)⊆N,表明car(t)∩car(s*)=Ø。

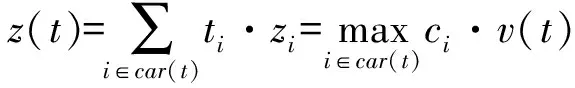
即，从最大广义模糊超量博弈均衡性视角，论证了在模糊凸合作博弈中，企业联盟的广义模糊核心与广义模糊谈判集分配方案具有等价性。

3 算例分析

“双循环”背景下，各企业通过组建联盟优化整合各自优势资源，追求“双循环”全局利益最大化。联盟通过优化谈判形成稳定的合作博弈格局，寻求最优广义分配方案，支持“双循环”背景下的持续合作。现设a1，a2，a3，a4代表具有合作意向的四家制造企业，结合成本、时间、技术互补等因素，决定组建联盟，合作研发完成新型供应链项目，记N={a1,a2,a3,a4}为合作企业集合，以下三种情况展示了联盟合作中形成的模糊凸博弈v及谈判过程。

情况I“双循环”背景下企业联盟合作形成的模糊凸博弈v的特征函数值如果满足

(5)

情况II“双循环”背景下企业联盟合作形成的模糊凸合作博弈v的特征函数值若满足

(6)

这只有

(7)

情况III“双循环”背景下企业联盟合作形成的模糊凸合作博弈v的特征函数值若满足

(8)

则不等式左侧的任意项均大于零，同时，其中任意三项之和一定比第四项的2倍大，比如:

(9)

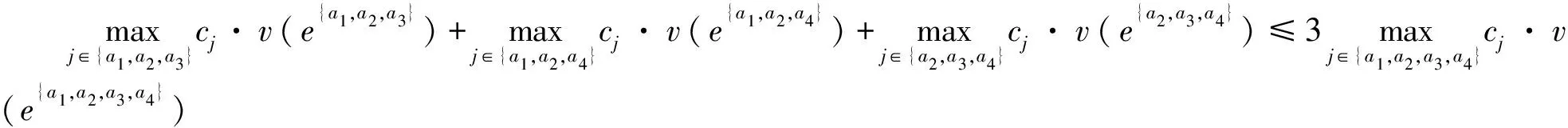
算例分析表明：四家科技型企业a1、a2、a3、a4，在“双循环”背景下合作形成的模糊凸博弈格局，具有最优广义分配方案，且广义模糊核心与广义模糊谈判集分配方案具有等价性质。同时，搭建企业联盟区域产业小循环模糊合作格局、构建广义模糊谈判集视角下驱动“内循环”向“外循环”的演化机制、提出企业联盟“双循环”最优广义模糊再分配方案决策建议等，均为企业联盟“双循环”持续合作提供优化对策。

4 结论

为实现企业联盟“双循环”产业链供应链合作转型，综合考虑区域小循环的不确定性及联盟合作的模糊特性，稳定模糊博弈关系的形成及驱动联盟持续合作分配策略的构建，对“双循环”高质量发展意义重大。基于广义模糊超量博弈均衡性的研究视角，针对企业联盟合作中形成的模糊凸合作博弈下，广义模糊核心分配方案与广义模糊谈判集分配方案的等价性进行论证，为企业联盟“双循环”合作格局及最优分配提供了新的研究路径。