资源受限下森林火灾应急救援多目标调度优化

王路兵, 吴 鹏, 胡 鹏, 储诚斌, 李慧嘉

(1.福州大学 经济与管理学院,福建 福州 350108; 2.北京邮电大学 理学院,北京 100876)

0 引言

21世纪以来，受全球变暖的影响，各种自然灾害频繁发生，给社会造成了严重的损失，特别是森林火灾。如2019年四川凉山的森林火灾、2020年美国加利福尼亚州和澳大利亚的特大森林火灾，其中澳大利亚的森林火灾造成28人死亡以及30亿动物死亡[1]。面对突发大规模森林火灾，如何在最短时间内组织科学、高效、快速的应急救援行动，合理调度安排消防救援车辆，用最短时间和最低成本扑灭森林火灾具有重要的现实意义[2]。

目前，针对灾害发生后的应急救援问题，国内外研究学者已经进行了大量的研究，如王妍妍和孙佰清[3]考虑灾害发生后不同阶段不同物资的需求与供给关系，提出多灾点、多阶段的应急物资分配模型，目的是使救援物资的分配成本和延迟成本最小。刘扬等[4]考虑救灾物资的需求不确定，提出多阶段救援物资调度模型，其旨在尽可能多地分配物资和最小化救援调度总行程时间。吕永波等[5]针对我国夏季部分地区容易发生洪水灾害问题，为及时准确地掌握受灾情况，减少灾情进一步蔓延，构建应急救灾物资分配模型，目的是合理分配救援物资和最大化救援效益。Garrido等[6]也考虑了洪水灾害问题，并构建最小化救援分配成本的优化模型。针对地震发生后的救援物资分配问题，李双琳和马祖军[7]考虑到震后通往灾区交通路网破坏的问题，提出实施交通管制措施，确保应急物资能够快速有效地送达灾区。王付宇等[8]针对地震发生后存在多个救援中心、多个受灾区域的情况，提出救援车辆两阶段调度优化模型，目的是使最大救援时间最短和伤员救援权重最大。Hu[9]考虑灾后集装箱多式联运的应急调度问题，提出多目标整数线性规划模型，目的是最小化救援车辆的总成本。石彪等[10]考虑大规模突发事件下的应急物资运输问题，提出两阶段车辆调度模型，目的是最小化应急救援时间。

从以上文献中，可以发现大多数研究主要集中在对地震、洪灾和其它自然灾害的应急调度，而对森林火灾的研究较少。据本文所知，对森林火灾的应急救援调度问题近些年才有相关学者开展研究。如杨忠振等[11]考虑森林火灾发生后消防车辆的调度问题，构建同时最小化消防车总运输时间和运输成本的双目标调度模型，并采用免疫克隆算法求解。Tian等[12]针对多起森林火灾同时发生后的消防车辆调度问题，构建最小化灭火时间和消防车数量的双目标优化模型，并采用差分进化算法和粒子群优化算法相结合的算法求解。Wu等[13]在上述研究的基础上，构建消防资源受限下的双目标优化模型，并提出动态规划算法和快速贪婪启发式算法求解。Ren等[14]考虑资源受限下森林火灾应急救援问题，构建以最小化消防救援队总的行程距离为目标的调度优化模型，并设计一类遗传算法和粒子群优化算法结合的混合智能算法对模型进行求解。随后，为有效求解上述资源受限下森林火灾应急调度问题，Wu等[15]建立优化模型，采用优化软件CPLEX求解。最近，吴鹏等[16]对森林火灾应急救援问题做进一步研究，考虑多消防车辆的应急救援问题，构建混合整数线性规划模型，并设计改进人工蜂群算法快速求解模型。

从上述研究可以发现，较少文献研究了资源受限下森林火灾应急救援问题，且尚未有研究报道资源受限下森林火灾应急救援多目标优化问题。同时，为减少火灾造成的损失，对火灾较为严重的区域应优先提供消防救援服务，以确保消防救援工作及时、有效的开展。本文根据森林火灾发生的特点，提出火势蔓延模型和灭火时间的计算公式，构建资源受限下多目标调度优化模型，目的是同时最小化消防救援时间和消防车辆总的行驶距离，并提出ε-约束法和模糊逻辑相结合方法对问题进行求解。最后，通过对不同参数下的计算结果进行对比分析，以了解参数变化对消防救援调度方案的影响。

1 森林火灾应急调度模型构建

1.1 问题描述

森林火灾突发后，消防救援中心需以最短的时间将救援物资送到受灾点。但由于森林火灾的发生具有很大不确定性，一旦突发大规模火灾，消防救援中心的救援资源可能无法同时前往所有的受灾点。此时，如何合理地安排消防车辆开展救援工作尤为重要。

为尽快扑灭火灾，根据火势蔓延速度划分不同的救援优先级，即火势蔓延速度越大，救援优先级越高，以便有针对性的开展救援工作，其救援过程如图1所示。从图1可知，本文主要研究森林火灾发生后由救援中心向多个火灾点派遣消防车提供救援服务的应急救援问题。同时，探究在消防资源受限下，如何对消防车辆进行合理的调度，从而最小化消防救援时间和消防车总行驶距离。在建立优化模型之前，提出如下假设：

(1)消防车辆的灭火速度大于火势蔓延速度，确保火灾能够及时扑灭；(2)火灾点的火势蔓延速度、数量以及两两之间的距离已知。

图1 消防救援路线图

1.2 火势蔓延模型和灭火时间的计算

火势蔓延速度受风力、燃料类型、地形坡度等诸多因素的影响，其计算过程的非常困难和复杂的。本文参考文献[11]的火势蔓延模型，具体如下所示:

v0=αT+βW+γ

(1)

vs=v0λsλwλφ=v0λsλwλφe0.1782vm

(2)

其中,v0为初始蔓延速度，vs为火势蔓延速度，其余参数介绍详见文献[11]。

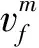
(3)

1.3 模型参数与变量

1.4 模型建立

综上所述，本文构建的多目标优化模型如下:

F1=minCmax

(4)

(5)

(21)

其中，目标函数式(4)为最小化消防救援时间；目标函数式(5)为最小化消防车总行驶距离；式(6)表示每个火灾点由一辆消防车服务；式(7)和(8)表示消防车从救援中心出发，在完成灭火后返回；式(9)为流平衡约束；不等式(10)为消防车的行驶时间限制约束；式(11)确保优先级较高的前|K|个火灾点优先被消防车救援；式(12)表示救援优先级较高的火灾点在救援优先级较低的火灾点之前被消防车服务；式(11)和(12)共同确保消防车按火灾点的救援优先顺序进行灭火；式(13)是消防车的出发时间；式(14)为灭火时间计算公式；式(15)为消防车辆到达火灾点的时间；式(16)表示计算消防车的最大救援时间；式(17)和(18)表示每个火灾点最多只能被消防车辆服务一次；式(19)～(21)为决策变量约束。

1.5 模型线性化

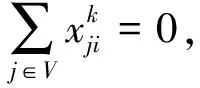
(1)如果火灾点i被消防车辆k服务，则约束式(15)左右合并可以表示如下:

(22)

(23)

(24)

(25)

其中Q是一个非常大的正数。

(26)

综上，式(15)的两种可能情况可以由等价线性约束式(24)～(26)共同表示，最终的线性化多目标优化模型可以表示如下:

F1=minCmax

s.t.(6)～(14)、(16)～(21)和(24)～(26)

模型经过线性化处理之后，能够降低计算方面的困难，并且对比非线性模型，能够更加快速求解。

2 基于ε-约束迭代和模糊逻辑相结合的算法

为了便于研究，本文将提出的多目标优化模型表示如下:

minF(x)={F1(x),F2(x)} s.t.x∈X

其中，x和X分别表示由约束式(6)～(14)、(16)～(21)和(24)～(26)形成的解向量和可行的解空间；F1(x)和F2(x)分别表示消防救援时间和消防车辆总的行驶距离；{F1(x),F2(x)}表示目标空间。

由于本文研究的两个目标最小化消防救援时间和消防车辆总行驶距离存在矛盾关系。因此，不存在单一的最优解使得F1和F2最优，而是一组Pareto解使其达到最优。对于本文优化的两个目标函数F1和F2而言，如果存在一个解向量x*，对于任意x，有F1(x*)≤F1(x)和F2(x*)≤F2(x)，且至少一个不等式是严格成立的，则称解向量x*为非支配解，即Pareto解。所有Pareto解可以在坐标系上形成Pareto前沿面，Pareto前沿面上的点不存在支配关系，并且这些Pareto点可以帮助决策者在F1和F2两个目标上做出权衡。

目前，通常采用加权法、目标法以及ε-约束法求解多目标优化问题，其核心思想是将多目标问题转化为一系列的单目标问题，从而获得一组Pareto解。对比三种方法，ε-约束法比前两种方法是更适用的，其避免了对目标函数进行缩放和设置适当权重的困难，但是ε-约束法不能帮助决策者在一组Pareto解中快速地找到最优解，而模糊逻辑技术可以帮助决策者寻找最优解。因此，本文提出ε-约束法和模糊逻辑相结合的算法对模型进行求解，不仅可以精确求解本文提出的多目标优化模型，还可以帮助决策者根据自身偏好选择最优解。基于ε-约束法和模糊逻辑相结合的算法步骤如下:

首先，本文经过分析，将作为主要优化目标，作为ε-约束条件，经ε-约束法转化后的模型如下:

F1=minCmax

s.t.F2≤ε

Eqs.(6)～(14)、(16)～(21)和(24)～(26)

εk=F2(εk-1)-Δ

(27)

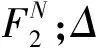
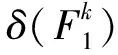
(28)

其中，μ1和μ2分别对应两个目标函数F1和F2的权重，即决策者对F1和F2的偏好，并且μ1+μ2=1。

3 算例分析

3.1 实例分析

本文以2010年中国大兴安岭山呼中地区发生的森林火灾案例进行研究[11]，这次森林火灾一共导致7处火灾点的发生。由于消防资源受限，消防救援中心只能安排3辆消防车对火灾点进行灭火。通过信息技术可以已知火灾点之间的距离、位置和火势蔓延速度，详细数据详见参考文献[11]。

本文通过对消防车辆的相关参数进行设置，以了解参数的改变对消防调度方案的影响。为此，本文拟定以下四种方案扑灭森林火灾，如表1所示。此外，还考虑了对两个目标函数设置不同权重下产生的实验结果，以便决策者更好地做出决策。四种方案中消防车辆的出发时间为0，然后采用C++编程同时结合CPLEX求解模型。此外，也采用LINGO求解器求解非线性模型，并与线性化后的模型进行对比，以验证线性化后的求解优势。具体实验结果如下所示:

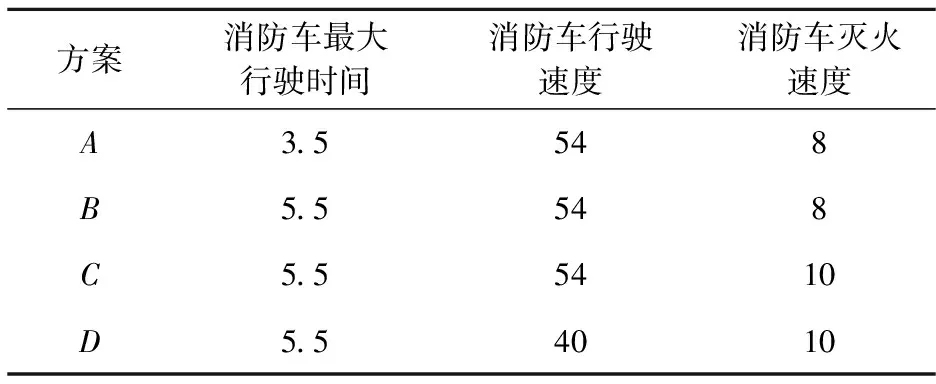
表1 四种方案的相关参数

表2 四种方案的计算结果

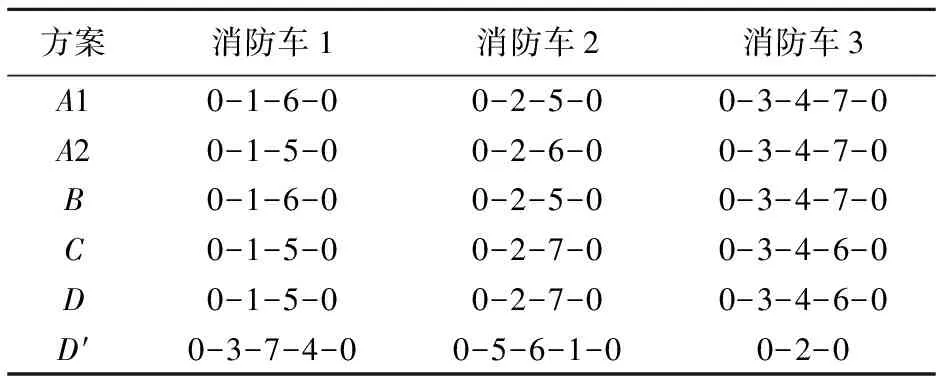
表3 μ1=0.5时消防车最优路径方案

表2为四种方案的计算结果，K在表2中，表示Pareto解的个数，μ1为目标函数F1的权重，TC和TL分别表示线性化模型和非线性模型的计算时间，D′是根据表1中D方案中的参数按照真实案例的执行方案得出的计算结果。表3为表2各个方案中μ1=0.5时所对应的消防车辆最优调度方案，其中，A1和A2表示方案A中μ1=0.5时对应的两种可行的调度方案，D′是真实案例执行方案下的消防车辆行驶路径。

文献中真实案例的执行方案采用的是就近救援原则，即对距离救援中心距离近的火灾点先进行救援，然后再对其它火灾点进行救援，目的是最小化消防车辆总行驶距离。如表2所示，虽然就近救援原则在一定程度上降低了消防车辆的行驶距离，但是却大大增加了灭火救援时间，从而造成大量的资源损失。与真实案例的执行方案不同，本文首先对每个火灾点进行救援优先顺序的划分。同时，考虑到消防救援时间问题，并建立多目标优化目标，目的是同时优化消防救援时间和消防车辆总的行驶距离。对比真实案例的计算结果，本文模型的求解结果虽然使消防车辆总的行驶距离增加了，但是与救援时间对比，能够极大地降低消防救援时间，比真实案例降低了约45.99%。

此外，根据表2和表3的结果：(1)对比方案A和B，如果消防车辆的最大行驶时间较长，则会有更多的消防调度方案，如A有2种可行的调度方案，而B却有5种；(2)对比方案B和C，消防车的灭火速度对救援时间影响很大，如在方案B中灭火救援时间需要14.55小时，而方案C只需7.19小时；此外，如果方案C在救援过程中实际灭火速度从10米/分钟降到8米/分钟，继续按照表3中的救援方案调度，那么救援时间将会从7.77小时增加至18.22小时，会造成大量森林资源损失，而如果选择B方案进行救援，那么救援时间将会从7.77小时增加至15.30小时，相比较而言，降低了消防救援时间；(3)同时，对比方案C和D可知，消防车行驶速度越高，救援时间越短，如在方案C中灭火救援时间只需7.19小时，而方案D却需要9.70小时，同时对消防车辆行驶距离也会有所影响；(4)此外，根据表3中C和D两种救援方案可知，当实际消防车辆行驶速度从54千米/小时降到40千米/小时，不会影响到消防救援方案，但会明显增加灭火救援时间；(5)根据表2可知，线性化后模型求解时间明显比非线性模型求解时间更短。

3.2 仿真算例分析

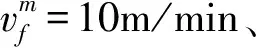
表4 4辆消防车的计算结果

表5 μ1=0.5时4辆消防车的最优路径

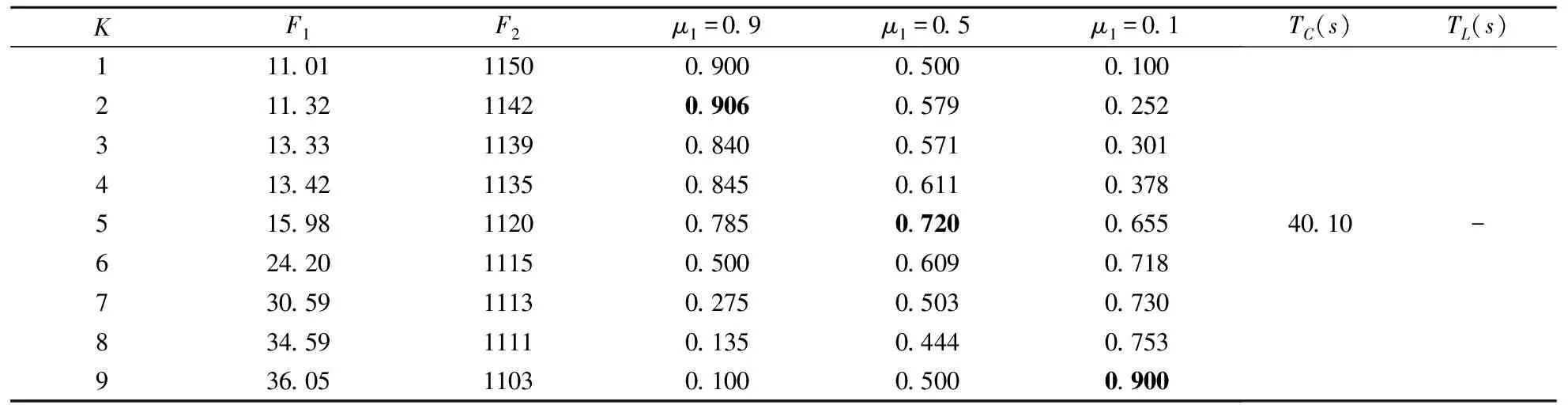
表6 5辆消防车的计算结果

表7 μ1=0.5时5辆消防车的最优路径

派遣消防车数量为4和5时，对应的实验结果如表4和表6所示，其中权重μ1=0.5时，对应的最优消防路径如表5和表7所示。

根据表4、表5、表6和表7的计算结果可知：(1)消防救援资源会对消防救援时间以及消防车辆的行驶距离产生较大影响，消防救援资源越多，产生的可行调度方案越多，不仅如此，随着消防车数量的增多，灭火救援时间明显减少；(2)对比表4和表6，消防车数量的增加会导致计算时间的增加，同时也会加大消防车辆总行驶距离；(3)考虑不同权重时，会对消防车辆调度产生很大影响，当权重μ1=0.1时，两种消防调度的最大灭火时间相同，此时安排4辆消防车具有更好的消防调度效果；此外，如表6和表7所示，消防车数量不同，对应的最优行驶路径也不相同；(4)实验结果表明，线性化模型均能够在不到一分钟内得到解决方案，这能实现森林火灾发生后第一时间内给出最优的消防调度方案，而非线性模型在10分钟限制时间内无法获得求解结果，说明本文提出的线性化模型能够加快求解速度。

4 结论

本文研究了资源受限下森林火灾应急救援问题，构建最小化消防车总行驶距离和消防救援时间的多目标优化模型，并提出ε-约束法和模糊逻辑相结合的算法对模型进行求解。综合分析了消防车辆的行驶速度、灭火速度、最大行驶时间和消防车数量的变化对消防调度方案的影响，并得出以下结论：(1)在森林消防灭火过程中，消防车辆总的行驶距离会影响到消防救援时间，在实际的消防灭火过程中需要同时考虑到消防灭火车辆总行驶距离与总灭火救援时间之间的关系，以便尽快扑灭火灾；(2)在应急救援过程中，为了降低森林资源损失，减少灭火时间，可以考虑事先增加消防资源的配备，如消防车的数量；(3)消防车辆的灭火速度可以在很大程度上减少灭火救援时间，决策者可以在森林火灾还未发生时，加强消防灭火设备的配置。

后续将进一步研究森林火灾的火势蔓延速度动态变化对消防调度方案的影响，以及考虑存在多个消防救援中心、多个火灾点的研究情况。此外，本文研究森林火灾救援问题并没有考虑到消防救援中心的选址问题。事实上，消防救援中心的选址直接关系到森林火灾发生后，能否快速有效地将消防资源送至火灾点，进行消防救援。因此，在接下来的研究中，也可以研究消防救援中心选址问题，并结合森林火灾发生频率确定最优选址位置，以确保尽快扑灭森林火灾，降低森林资源的损失。