突发事件下应急物资多目标优化调度模型与算法研究:以新冠肺炎疫情为例

2023-03-02单子丹盛晨辉王晓燕

运筹与管理 2023年1期

单子丹, 盛晨辉, 王晓燕, 韩姣

(1.哈尔滨理工大学经济与管理学院,黑龙江哈尔滨 150040; 2.哈尔滨理工大学高新技术产业发展研究中心,黑龙江哈尔滨 150040)

0 引言

2020年初，新冠肺炎在全国蔓延，彻底打乱了国民社会生活秩序和经济发展进程。突发事件应对过程中所需要的各类生命救助、防护用品等合称为应急物资，是成功应对突发事件的基本保障[1]。二月上旬武汉各大医院陆续向社会发布接受抗疫物资捐赠公告，急需进行医疗物资的紧急调度。如何以最合理、高效的运输方式将物资在所需时间内送达是此次疫情期间物资跨区域调度亟待解决的突出问题。

目前国内外学者从不同视角出发，对应急物资调度问题进行了较为广泛的研究。在应急物资调度过程中，救援时间能够实现最短是大多数学者考虑的首要因素[2-3]。考虑到灾后路网受损等特殊情况，学者们结合多种运输方式探索物资调度方式[4-5]。同时也考虑到了灾后物资需求存在着高度不确定性[6-7]。根据配送网络级数不同常常分为二级和三级调度网络，现有研究大多数为二级配送网络[9]。学者们多以成本与时间作为模型构建目标[3-4]。为了有效求解应急物资调度问题，近年来国内外学者将研究热点转向了进化算法[9-10]。粒子群算法相对于其他智能算法具有实现容易、收敛速度快、求解质量高等优势，在应急管理领域已经得到了广泛的应用，但易产生早熟收敛，针对这一问题对粒子群算法进行了改进用于模型的求解。

可以发现，大多数学者对于三级配送网络研究较少。事实上，新冠肺炎应急物资调度具有区域波及范围广、跨区域协调强度大等特点，在模型构建目标、择优方式及约束设计上有别于以往研究，且现有研究提出的多方式运输大多基于路网损毁情况下，路网尚好情况下大多是单一车辆运输方式。因此提出了包含多周期、多集散点、配送中心、需求点和运输方式的多目标优化调度复杂网络模型。

1 问题描述与模型假设

1.1 问题描述

基于上述分析，疫情发生后，构建集散-送中心-需求点三级调度网络。考虑物资需求的紧迫性、物资送达时间要求的特殊性、运输成本的经济性，本文采用航空和公路运输相结合的运输方式来柔性选择运输方式。结合在不同周期应急物资需求和供给存在动态变化角度，建立如下物资调度网络，示意图如下图1:

图1 两阶段多周期应急物资动态调配示意图

1.2 模型假设

结合应急物资的调度特征，做出如下假设:

(1)每个周期集散中心的供给量和需求点的需求量已知，且供给量不会超过需求量。

(2)集散中心至配送中心至需求点间道路相通可以进行长期的物资调配。

(3)不同类别的应急物资在不超载的前提下可由同一运输工具进行装载。

(4)以一天(24h)为一个决策周期，所有周期的物资起运时间均为0时刻。

2 动态多阶段应急物资调度模型构建

2.1 符号说明

(1)集合符号

集合符号含义集合符号含义I物资集散中心集合(i∈I)J应急物资配送中心集合(j∈J)M疫情需求点集合(m∈M)K应急物资种类集合(k∈K)N物资配送周期集合(n∈N)H集散中心至配送中心的运输方式集合,H={α,β}

(2)参数符号

参数符号符号含义Snikn周期应急物资集散中心i对物资k的供给量Rnikn周期末应急物资集散中心i对物资k的库存量Rnjkn周期末应急物资配送中心j对物资k的库存量Dnmkn周期疫情需求点m对应急物资k产生的当周期需求量Lnmkn周期疫情需求点m对应急物资k产生的短缺量Snijn周期应急物资集散中心i向配送中心j运输的最大供应量Snimn周期应急物资配送中心j向疫情需求点m运输的最大供应量Cnhijn周期使用运输方式h从集散中心i向配送中心j的单位运输成本Cnjmn周期配送中心j向疫情需求点m运输的公路运输单位成本dij应急物资集散中心i和应急物资配送中心j之间的距离djm应急物资配送中心j与疫情需求点m之间的距离Qkk物资的单位重量,gVnhijn周期使用运输方式h从应急物资集散中心i至配送中心j的速度Vjm应急物资配送中心j至需求点m的公路运输行驶速度tnikn周期从i地开始运送物资k的时刻tnijn周期从应急物资集散中心i至物资配送中心j的道路通行时间tnjmn周期从应急物资配送中心j至疫情需求点m的道路通行时间tnjkn周期应急物资到达配送中心j后必要的装卸搬运作业时间tnmkn周期应急物资k送达疫情需求点m的时间

(3)决策变量符号

决策变量符号含义xnijkn周期从应急物资集散中心i至配送中心j运输应急物资k的数量xnjmkn周期从物资配送中心j至疫情需求点m运输应急物资k的数量

2.2 时间窗下的物资调度惩罚函数

①硬时间窗约束[ET,LT]。ET和LT分别为最早和最晚送达时间。物资只有在此时间段内送达才能被接受。

②软时间窗约束[EET,ET)。EET为适当放宽的早送达时间上限，同时需要根据早送到的时间长短接受惩罚。

③软时间窗约束(LT,ELT]。ELT为适当放宽的晚送达时间上限，同时需要根据晚送到的时间长短接受惩罚。

④[0,EET),(ELT,-)，在这两个时间窗内送达的物资均违反了软硬时间窗约束。

考虑疫情期间对物资需求的紧迫性，物资送达时间应越早越好，晚送达会产生相应惩罚成本，因此疫情下物资送达时间窗的约束如图3。不同需求点相应非线性惩罚函数如式(1)。

图2 混合时间窗惩罚函数示意图

图3 疫情下需求点时间窗示意图

(1)

2.3 三级跨区域动态调度模型建立

疫情爆发初期患者人数激增，医疗物资产生了大量缺口，长时间短缺不仅会错失治疗患者的最佳机会，还会带来巨大的心理恐慌，因此尽可能降低物资短缺是模型建立的首要目标。

(2)

其中，f1即n周期所有疫情需求点的各种物资需求短缺程度值的总和。βm为m地的应急物资需求紧急程度。

需求点根据疫情情况确定物资送达时间窗口，应急物资应尽可能实现在所需时间内送达，由此建立时间窗约束下惩罚函数如下式(3):

(3)

其中，f2为n周期所有需求点在软-硬混合时间窗约束下的总惩罚成本。

大批量多批次长距离运输会产生较高的运输费用，出于经济性考虑，将运输成本作为目标函数的评价依据，表达式如下式(4):

(4)

其中，f3为n周期物资的总运输成本，α表示航空运输，β表示公路运输。

由上述分析，应急物资调度模型构建如下:

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

3 模型求解与启发性算法

3.1 多目标函数的转化

上述模型三个目标函数分属不同量纲。蒋杰辉等在论文中引入时间成本系数，将多目标函数转化为单目标函数[12]。借鉴此思想，引入短缺时间成本系数μ，将多目标函数转化为单目标函数并将三个权重系数分别设置为μ1、μ2和μ3。从而转化为如下单目标函数:

minF=μ1·F1+μ2·F2+μ3·F3

(22)

3.2 改进粒子群算法的应用

3.2.1 粒子群优化算法

粒子群优化算法由两位学者受鸟群捕食现象启发提出的智能算法[13]。粒子通过跟踪个体和群体极值来更新自身位置和速度即:

(23)

(24)

3.2.2 改进DCWPSO算法

为解决粒子群算法早熟收敛问题，有学者对惯性权重ω进行了深入研究。Shi Y提出了线性递减惯性权重策略[14]:

(25)

其中iter为当前迭代次数，ω变化只与迭代次数线性相关。文献[15]通过实验证明动态变惯性权重自适应粒子群(DCWPSO)算法性能明显优于LDW算法，引入聚焦距离变化率概念。

(26)

(27)

(28)

(29)

其中，MaxDist和MeanDist分别为最大和平均聚焦距离。本文在此基础上，引入变异算子，使得收敛速度和精度进一步优化，简称此算法为VDCWPSO算法。具体流程图如下：

图4 VDCWPSO算法流程图

3.3 实例计算与分析

3.3.1 问题实例

以新冠肺炎为背景，数据来源于武汉市部分区新冠肺炎真实数据和部分仿真数据，本文选取2月24日至29日疫情数据，选如下部分区作为需求点：江岸区、江汉区、汉阳区、武昌区、青山区、江夏区。将天河机场和汉南机场作为配送点；合肥、西安作为集散点；选取医用防护口罩、医用防护服、84消毒液作为调配物资。其中合肥和西安距离天河机场分别为447和762km,合肥和西安距离汉南机场分别为437和769km。天河机场距离江岸、江汉、汉阳、武昌、青山、江夏区分别为28，24，32，32，36，59km，汉南机场距离六区距离分别为51，50，42，52，65，43km。六区物资送达时间窗要求为LT:14，5，13，4，14，15时，ELT：16，6，15，6，15，16时。航空和公路运输单价分别为1700和20元/t/h，平均速度分别为500和80km/h，其中航空运输单价参考上海机场货运公司上海至武汉航线500kg以上货物2.6元/kg价格，公路运输速度取高速公路运输最高与最低限速平均值。

表1 六个疫情需求点的基本情况(单位：例)

表2 集散中心各阶段应急物资供给量

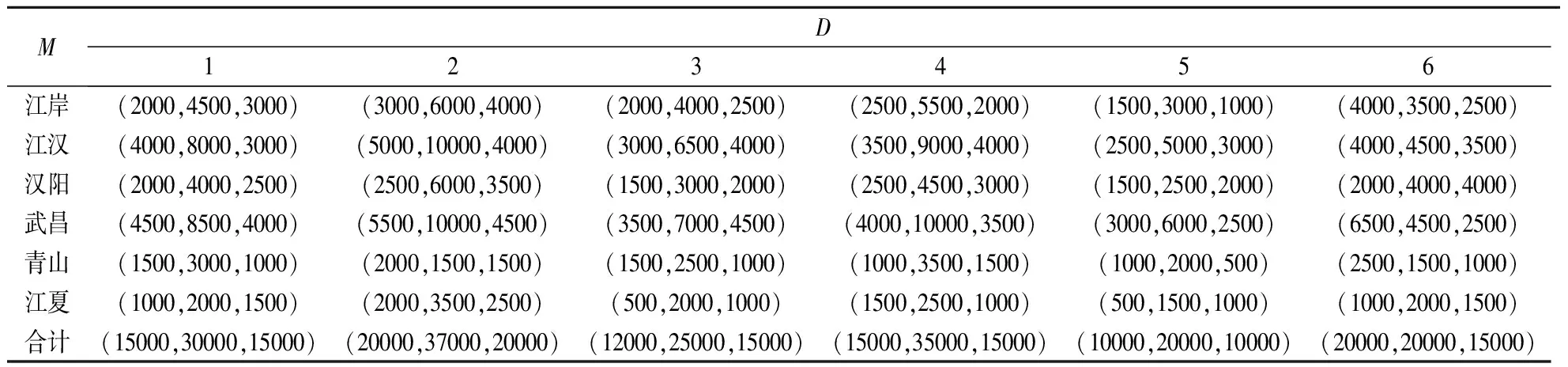
表3 疫情需求点各阶段应急物资需求量

3.3.2 算例结果分析

通过MATLAB编程实现，对比DCWPSO算法和遗传算法验证本算法有效性，μ1、μ2、μ3设置为0.4,0.4,0.2,此权重考虑了弱经济性。由于篇幅有限，各周期集散点至配送点和配送点至需求点运送物资数量不做详细陈述，仅选取第五周期物资最优调配方案如表4,表5。

表4 第五周期物资最优调配方案(第一阶段)

表5 第五周期物资最优调配方案(第二阶段)

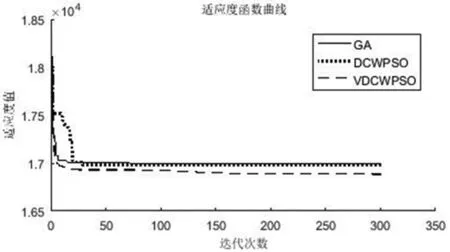
图5 [0.4,0.4,0.2]权重下适应度函数曲线图

图6 [0.6,0.3,0.1]权重下适应度函数曲线图

图7 [0.2,0.6,0.2]权重下适应度函数曲线图

图8 [0.2,0.2,0.6]权重下适应度函数曲线图

上四图为不同权重组合下三种算法适应度函数曲线对比图。从图中可看出运输成本占函数值比重较大，函数曲线在迭代初期波动较大，随着迭代次数增大，曲线趋于平缓。从图中可看出本文所提算法适应度函数值最低，可见本文提出的算法更能有效求解所提出的问题。在本算法迭代过程中，从曲线倾斜程度可看出，初期函数值变化幅度较大，算法收敛效率较高。