AC/NS-DBD 等离子体激励分离剪切层的涡量输运特性

赵光银，杨永东，李婷婷，肖春华，阎 丽

(中国空气动力研究与发展中心 低速空气动力研究所，四川 绵阳 621000)

0 引 言

近二十年，等离子体气动激励在流动控制领域的应用受到广泛关注和深入研究。相较于传统的流动控制手段，等离子体激励器结构简单，不改变原有气动型面，且等离子体气动激励响应快（＜0.1 ms）、频带宽（0.01～100 kHz），具有实时自适应闭环流动控制的优势。

不同结构形式的等离子体激励器可产生不同的等离子体气动激励，比如用于流动分离控制的表面介质阻挡放电（dielectric barrier discharge, DBD）激励、用于激波控制的表面电弧放电激励[1]、基于火花放电原理产生的等离子体合成射流激励[2]等。文献[3]综述了多种典型等离子体气动激励的特性和应用，其中就流动分离控制而言，国内外对表面DBD 的研究最为广泛和深入。

典型的表面DBD 激励器由绝缘介质和两侧非对称布置的高低压电极组成。根据驱动电压的波形和时间尺度，可产生交流（AC-）[4]、微秒脉冲（μs-）[5]、纳秒脉冲（NP-）[6-7]等不同原理的等离子体气动激励。普遍认为AC-DBD 激励的原理是动量输入，基于动量输入的流动控制强度可用动量系数或速度比（激励诱导速度与附面层外边界速度之比）表征，ACDBD 激励的诱导气流速度小于10 m/s，这使得其在高速流动控制中面临能力不足的问题。

纳秒脉冲表面DBD（Nanosecond dielectric barrier discharge, NS-DBD）激励的基本原理是，当驱动激励器脉冲高压的上升沿时间尺度在几纳秒到几十纳秒的量级时，放电会在等离子体层迅速沉积能量，导致局部气体在1 μs 内被快速加热，引起局部气体压力快速升高，对流场形成强脉冲扰动甚至是冲击波扰动[8]。

在表面DBD 等离子体分离控制研究中发现，非定常等离子体激励的控制能力显著优于定常激励[4]。相比AC-DBD 激励，NS-DBD 激励的流动控制能力更强[8]。NS-DBD 激励已被验证在起飞/着陆来流条件下能够推迟机翼失速[9]；在Ma= 0.74 时可有效抑制翼型绕流分离[6]；在Ma= 0.5 时可有效改善超临界翼型和后掠飞翼布局的气动特性[10]。

文献[11]通过二维锁相PIV 研究了AC-DBD 激励和NS-DBD 激励在翼型大迎角分离控制上的区别，比较了两种激励诱导展向涡的位置、结构和强度，发现NS-DBD 激励可以诱导出更强的扰动；然而整体上，分离流场对这两种激励的响应相似，诱导展向涡结构的区别并不大。

非定常AC-DBD 激励和NS-DBD 激励均可以形成非定常扰动，使前缘分离剪切层失稳，诱导出宏观的展向涡结构；但是两种不同原理（动量输入和热量注入）的激励在流动控制上的机理有何不同仍需进一步研究。为深入理解AC-DBD 激励和NS-DBD 激励在诱导展向涡形成上的区别，本文引入二维涡量动力学方程，分析了两种激励诱导展向涡的涡量源，对等离子体流动控制给出了更进一步的研究。

1 数值模拟方法

1.1 流动控制方程

其中：ρ为流体密度；ui为时间t时坐标xi处的速度分量，i= 1、2、3 分别对应笛卡尔坐标系下的x、y、z方向；p为压力；T为温度；E为单位质量流体总能； δij是克罗内克δ函数符号，当i=j时， δij= 1； τij是黏性应力在（i，j）上的张量分量，各变量的具体形式参见文献[12]。假设气体为完全气体，导热系数由拟合式λ=0.004 36 + 0.000 074T给出，动力黏性系数 µ由Sutherland定律计算。

研究认为NS-DBD 激励诱导速度很低[13]，可忽略其放电过程中的体积力效应，在计算NS-DBD 激励流动控制时，可设置动量源项f为0；AC-DBD 激励以动量效应为主，可忽略其放电过程中的瞬间热效应，在计算AC-DBD 激励流动控制时，设置能量源项Q为0。

对Navier-Stokes 方程进行雷诺平均处理后，动量方程和能量方程里出现了非线性雷诺应力项 −ρu′iu′j，需要引入湍流模型使方程封闭。其中出现了直接处理雷诺应力项的雷诺应力模型和不直接处理雷诺应力项的涡黏模型。雷诺平均模型中的涡黏模型多采用各向同性的湍动黏度来计算湍流应力，这些模型难以考虑旋转流动和流动方向表面曲率变化的影响，雷诺应力方程模型（Reynolds stress model, RSM）则可克服这些缺点。根据雷诺平均后的Navier-Stokes（RANS）方程中的动量方程，取二维情况，对其中的x、y方向的动量方程取旋度。

进一步整理可得二维RANS 方程对应的涡量输运方程[14]：

其中：u′1表 示x方向速度u1的 脉动量，u′2表示y方向速度u2的脉动量；x1、x2表示x、y方向坐标；式（6）右端最后三项表征了雷诺应力对z向雷诺平均涡量（ ω3）的影响。从揭示流动控制机理的角度看，涡黏模型已经难以满足要求。从二维情况（式（6））可知，法向应力对展向涡量的发展有一定影响。因此采用各项异性湍流模型对研究与展向涡相关的流动控制机理是有必要的。同时，文献[14]认为，相比于涡黏模型，对于翼型绕流分离的计算，RSM 可以得到更接近大涡模拟的结果。对于LES 计算得到的大尺度分离情况，涡黏模型需要调整最大湍动黏度来获得；而RSM 由于没有引入Boussinesq涡黏假设，则不需要这一调整。本文采取RSM，该模型在文献[15-17]中有详细介绍。

1.2 实际流体的涡量输运方程

常见的涡量输运方程有不可压、黏性不变的形式，也有可压、黏性不变的形式。对于密度和温度变化较为剧烈的流动，必须考虑密度和黏度的变化，以实际流体的Navier-Stokes 方程[18]推导涡量输运方程。

对方程（2）两端求旋度，得到涡量输运方程[19]：

涡量输运方程推导中一般假设动力黏性系数μ为常数，在不可压黏性流中斜黏项并不存在。当密度变化剧烈时，NS-DBD 激励瞬间的能量释放引起局部瞬间温升（可达500 K 以上），使黏性和密度均产生明显变化，与黏性相关的斜黏项不应忽略。该项的存在表明，即使在流场内部（非固壁边界处），可压流体在黏性的作用下也具有产生涡量的能力。

1.3 翼型、网格及等离子体激励

选取二维翼型（NACA 0012）的大迎角（α= 20°）绕流产生分离剪切层，进而对该分离剪切层分别施加AC-DBD 和NS-DBD 等离子体激励。取翼型弦长c= 0.353 m，Re= 7.5 × 105，Ma= 0.1。采用O 型网格对计算区域离散；周向网格640 个，径向网格369 个，网格数量23.6 万；壁面法向第一层网格高度为2 ×10−5c。在翼型上表面前缘附近进行网格加密，设距离翼型前缘15 倍弦长处的圆形边界为远场边界，翼型水平放置，翼型前缘顶点为坐标原点。

很多学者建立了AC-DBD 激励的体积力模型[22]和NS-DBD 激励的热源模型[6,23]。本文采用文献[24]建立的NS-DBD 激励热源模型，将NS-DBD 激励以瞬间热源的形式耦合到流体控制方程。翼型前缘处表征NS-DBD 激励的热源分布如图1（a）所示；表征AC-DBD 激励的体积力模型如图1（b）所示。

图1 表征两种激励的源项分布Fig.1 Heat source and body force (Fx, Fy) distribution of the two types actuations

2 计算结果及分析

在基准流场计算达到稳定后，选取某一时刻t1，分别施加非定常AC-DBD 激励和NS-DBD 激励。其中热源的施加时间为1 μs，体积力的施加时间为100 μs（对应占空比为10%，脉冲频率为1 000 Hz 的AC-DBD 单次激励持续时间）。在整个计算期间，采取的时间步长均为0.01 μs。对于短脉冲等离子体激励，激励期间不考虑源项随时间的变化。提取激励施加完毕时的t2时刻和激励施加结束后 Δt= 0～3 ms时刻的流场进行分析（时序示意图如图2 所示）。

图2 两种激励下选取的流场时刻示意图Fig.2 Schematic diagram of the time instances selected under the two types of actuations

2.1 宏观流态和涡量分布

图3 给出了激励施加后 Δt= 0～3 ms 的涡量分布和流场结构。在 Δt= 0 时，激励刚施加完毕，局部扰动在前缘刚形成，还未来得及发展，因此AC-DBD 和NS-DBD 两种激励区下游流场结构一致。而在前缘激励处壁面涡量有明显不同，AC-DBD 激励处产生了明显的正向涡量增量，NS-DBD 激励处产生以正向为主、负向为辅的涡量增量分布。 Δt= 1 ms 时（流态介于 Δt= 0 和 Δt= 2 ms 之间，为缩减幅面结果未展示），激励形成的扰动随剪切层向下游运动，经过分离区被放大，逐渐发展成为展向涡结构。相比之下，NSDBD 激励诱导的展向涡结构形成稍快于AC-DBD 激励，展向涡结构较为明显。 Δt= 2、3 ms 时，诱导展向涡结构更加明显，AC-DBD 激励对应的展向涡结构在弦向位置上略微滞后于NS-DBD 激励。后面发现这与AC-DBD 激励的方向有关，当AC-DBD激励反向作用时，基本不会出现滞后现象。除了在展向涡结构位置上有一些差异，单从流态上很难分清两种激励在流动控制上的区别。

图3 两种激励后不同时刻局部涡量云图和流线Fig.3 Local vorticity and streamline at different time instances for the two types of actuations

另外，从翼面压力分布上看（如图4），激励后 Δt=3 ms 时，两种激励下的翼面压力分布趋势一致，均是展向涡处对应了一个负压区，负压幅度基本一致，很难区分出以热量注入和动量注入为原理的两种等离子体激励方式引起的控制机理有何不同。

图4 激励施加后不同时刻的翼面压力系数Fig.4 Pressure coefficients at different time instances after the actuation

2.2 激励施加后的涡量净增量

为量化激励引起的流动变化，将激励后流场的参数减去对应时刻的基准流场，得到流场变量的净增量，分析激励对流场的影响。

AC-DBD 激励施加结束时（ Δt= 0），在前缘激励处诱导的涡量增量Dω是正涡量（图5（a）），下游近壁面处有一层负涡量区。激励后的速度增量（DVx,DVy）形成了明显的逆时针涡结构。 Δt= 1 ms 时，扰动随剪切层向下游运动，涡量增量逐渐发展为正负交替分布，速度增量对应的主要涡结构是逆时针的（图5（c））。

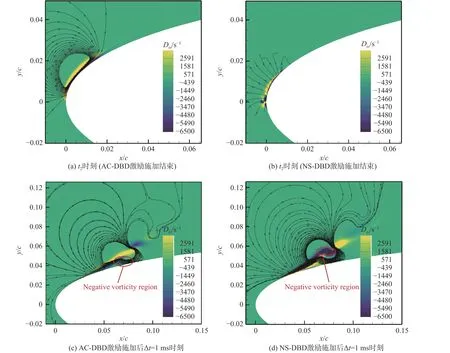
图5 两种激励后不同时刻诱导出的流场变化Fig.5 Flow field variations at different time instances induced by the two types of actuations

而NS-DBD 激励施加结束时（ Δt= 0 ms），在前缘激励处诱导的涡量增量基本上是左负右正（图5（b）），对应的速度增量（DVx,DVy）很小，并没有形成明显的涡结构。 Δt= 1 ms 时，涡量增量发展为正负交替的分布，速度增量对应的主要涡结构是顺时针的（图5（d））。AC-DBD 激励持续时间为100 μs，远高于NS-DBD 激励的1 μs，使得激励结束后，AC-DBD 激励对应的Dω范围大于NS-DBD 激励（图5（a、b））。

对于NS-DBD 激励，速度增量（DVx,DVy）的方向由激励区向外呈辐射状（图5（b）），像一个“爆炸”的流态，说明激励之后产生瞬间的流体膨胀，具有顶起剪切层的作用，向后发展的过程中（图5（d））形成的涡量增量分布与AC-DBD 激励情况相反。这逐渐影响了后续展向涡的形成与发展。控制中起主导作用的展向涡是负涡量的顺时针结构（见图3）。

对照图3 和图5，在 Δt= 2 ms 时，负的涡量增量Dω发展成明显的展向涡结构。由于AC-DBD 激励诱导中左侧贴壁处的负涡量（图5（c））最终发展成了展向涡结构，其位置相对于NS-DBD 激励（图5（d））中的负涡量位置更靠近前缘，这最终导致了在激励施加后的同一时刻，AC-DBD 激励的展向涡位置稍靠上游。

AC-DBD 激励诱导的逆时针速度增量引起的正涡量随着剪切层传播到了下游，这其实对展向涡（负涡量，顺时针）起到了一定的抵消效果。从控制效果分析，如果采用反向的AC-DBD 激励，应该会避免这种涡量的抵消现象，起到更好的控制效果。为此，在与图1（b）激励位置和体积力分布相同的情况下，仅改变体积力的方向（与图1（b）方向完全相反），开展相同流场状态下反向AC-DBD 激励的计算，结果如图6 所示。在激励施加结束时，前缘激励处的涡量增量与正向激励相反（与图5（a）比校）。在激励施加后Δt= 1 ms 时，展向涡量的增量和涡结构（图6（b））与NS-DBD 情况（图5（d））类似。反向AC-DBD 激励诱导的涡量增量与后续剪切层失稳形成的展向涡量和涡结构方向一致，可以起到增强展向涡的效果。图6（c）给出了在正向和反向AC-DBD 激励后Δt= 0～3 ms 内的翼型升力系数的响应曲线。在激励结束后 Δt＜ 1.5 ms内，两种方向AC-DBD 激励下的翼型升力系数很接近；随着展向涡的形成与发展（ Δt＞ 1.5 ms 以后），反向AC-DBD 激励引起的升力系数相对较大，或者升力系数提升相对较快。

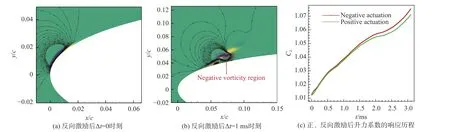
图6 反向AC-DBD 激励施加结束后不同时刻的涡量净增量和升力系数响应Fig.6 Net increment of the vorticity and the lift coefficient response at different time instances for the reverse AC-DBD actuation

2.3 激励施加时的涡量变化

在激励施加快要结束的t2时刻，对涡量动力学方程的各项进行分析，此时的扰动还未来得及传向下游，主要对比前缘激励区附近的涡量变化。图7 给出了两种激励（正向AC-DBD 激励和NS-DBD 激励）下各自的涡量 ω、涡量当地变化率 ω˙、 对流项 ω˙A、膨胀项ω˙C、 斜压项 ω˙B和 黏性项 ω˙D；此外对AC-DBD 激励给出了体积力项 ω˙E，对NS-DBD 激励给出了黏性项中的斜黏项 ω ˙D2。

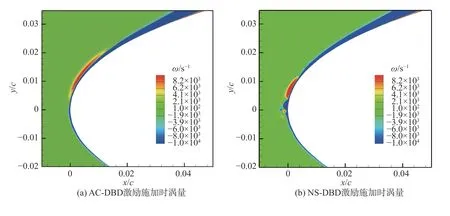
图7 两种激励施加时（t2 时刻）涡量及其动力学方程的各项分布Fig.7 Distributions of the vorticity and different terms in the vorticity evolution equation for the two types of actuations

先分析涡量变化率，两种激励下涡量变化率明显不同，NS-DBD 激励区的涡量变化更为剧烈（图7（d）），而AC-DBD 激励的涡量变化主要在近壁面区（图7（c）），量级上低于NS-DBD 激励。两种激励下的涡量变化率分别对应了图7（a、b）中涡量的分布。

对比当地涡量变化率各项组成，对于AC-DBD激励，对流项和体积力项起主要作用，其余项量级较大的部分集中在壁面，壁面以外量级较小。在ACDBD 激励施加时，空间非均匀分布的脉冲体积力是涡量增量的主要来源。对于NS-DBD 激励，此时斜压项和对流项构成了涡量变化率的主要成分，在分布和方向上与涡量增量一致；由于温升和压升明显，NSDBD 激励对应的膨胀项比AC-DBD 激励情况明显；黏性项集中在前缘紧贴壁面处，量级相对较低。在NS-DBD 激励施加时，空间非均匀分布的瞬间热流引起的斜压效应是涡量增量的主要来源。

值得说明的是，黏性项中有一部分是斜黏项（如图7（n）所示）。此时斜黏项 ∇(1/ρ)×(∇·τ)相对斜压项∇(1/ρ)×∇p要低3 个数量级，二者方向一致。原因是瞬间的温升引起了密度的剧烈变化，在黏性应力作用下也会产生涡量。斜黏项和斜压项的不同是这两种激励诱导展向涡量来源的一个重要区别。

与NS-DBD 激励不同，非均匀分布的体积力作用是AC-DBD 激励的主要涡量来源，其次是对流引起的涡量变化（非源）；而NS-DBD 激励瞬间的温升和压升使气体密度来不及变化，这一过程可假设为定容过程，会引起很大的斜压作用，从而形成NS-DBD 激励的主要涡量源。

2.4 展向涡形成后的涡量特性

激励施加结束之后（动量源项和能量源项为0），仍需探究激励形成的扰动对下游涡量发展的影响。对于NS-DBD 激励，斜压矩是一个明显的不同之处，然而激励形成的压力梯度难以维持，温度也会很快降低。在本文设置的NS-DBD激励强度下，激励区最大温度达到1 400 K， Δt= 1 ms时流场最大温度为317 K，Δt= 2 ms 时流场最大温度为304 K， Δt= 3 ms 时流场最大温度为302 K。根据涡量的变化和涡结构的发展（图3），选取展向涡结构发展明显的 Δt= 2 ms 时刻分析涡量动力学方程各项的大小（图8）。

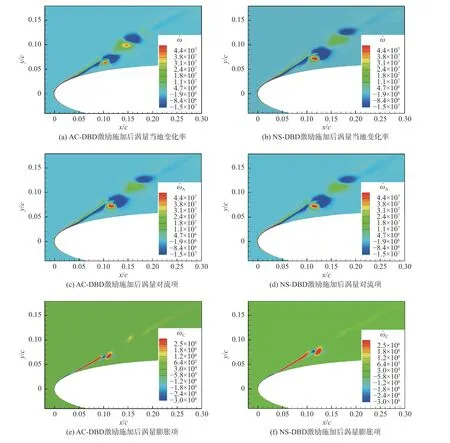
图8 两种激励施加后Δ t=2 ms 时涡量及其动力学方程的各项分布Fig.8 Distributions of the vorticity and different terms in the vorticity evolution equation at 2 ms after the two types of actuations

对流作用使展向涡结构处涡量分布增大。从膨胀项与涡量的分布看，膨胀作用减小了当地涡量。展向涡处温度较高，密度较低，流体膨胀现象明显，涡核处膨胀项为正，使负涡量减弱。除NS-DBD 激励下的展向涡核处稍大一些外，两种激励下的膨胀项分布和量级一致（图8（e～f））。

一方面，斜压的作用体现在前缘壁面附近（图8（g～h）），翼型前缘处的通道效应使得流动先加速降压、后减速增压，斜压项在上翼面前缘壁面处对涡量的产生起到促进作用，此时两种激励下的斜压项在前缘剪切层处的分布一致；另一方面，斜压的作用体现在展向涡结构形成处，此处NS-DBD 激励的斜压项更为明显。根据完全气体关系p=ρRT，激励区域的温度梯度较大，引起了密度梯度和压力梯度的不平行。对于AC-DBD 激励，由于无热量注入，该区域的温度梯度较小，斜压效应相对不够明显。

从图8（k、l）可以看出，虽然斜黏项的大小相对其他项较小，但其正负性基本与Dω一致，说明其产生的涡量促进了Dω的生成，进而促进了展向涡量的产生。黏性扩散项在前缘壁面附面层内促进壁面涡量的产生；在随剪切层向后演化过程中，与展向涡量的方向相反，说明其减弱了展向涡量。

两种激励下黏性项中的扩散项分布和大小一致，展向涡结构处有细微差别，主要原因是该处温度不同，黏性系数较高的位置扩散项较大。相对于剪切层处的黏性扩散项，展向涡处的扩散项量值较小。

流场中温度较高的一部分在展向涡处，另一部分在紧贴壁面的前缘分离点附近。斜黏项只有在上翼面温升较高的近壁面分离点处明显为正（该处的斜压项为负，局部存在逆压梯度），而在前缘剪切层处和展向涡处为负，这说明该项对展向涡的形成起到了促进作用。前缘剪切层处，附面层最薄，剪切最为强烈，黏性力的“撮”涡效应明显。

对于AC-DBD 和NS-DBD 两种激励，展向涡结构处当地涡量的变化主要是对流引起的。从随流导数的角度，对流项和当地变化项并列存在，二者意义不同，共同构成涡量变化率；如果单从固定点的角度看，运动流体的对流作用可导致当地涡量的变化。

对于NS-DBD 激励，在激励之后形成的展向涡处，存在一个有限作用的斜压矩和斜黏矩，其影响相对AC-DBD 激励较为明显，这是NS-DBD 激励之后滞留的热流引起的温升所致。但是斜压项和斜黏项的量级相对其他项并不大。从量级上看，斜压项已经从激励时的主导地位逐渐降为次要地位，随着展向涡向下游运动，斜压效应逐渐减弱。文献[24]针对NSDBD 激励对流场的效应分别对单纯温升（不引起压升）和单纯压升进行模拟，得出单纯温升时，诱导展向涡的强度和结构并不明显，因此只能说斜压项和斜黏项对激励后下游涡量的变化起到的加强作用有限。

由随流导数（式（7））可知，激励在激励区产生壁面涡量后，运动流体单元的涡量随剪切层和流动分离进入流体内部。激励间歇期，壁面涡量增量向下游传播，受黏性影响，此时随流涡量的来源除黏性作用外，就只有斜压项，然而斜压项对AC-DBD 激励的效应微乎其微，在黏性的扩散效应作用下，展向涡的涡量最终会在运动过程中逐渐耗散。

3 结 论

为深入理解NS-DBD 激励和AC-DBD 激励在分离控制上的区别，本文在Ma= 0.1、Re= 7.5 × 105的来流条件下，数值研究了两种激励对翼型大迎角（α=20°）绕流分离的控制。对于AC-DBD 激励，强调其动量效应，忽略其热量效应；对于NS-DBD 激励，主要强调其热量效应，忽略其动量效应。将NS-DBD 激励和AC-DBD 激励分别以空间分布的热源和动量源项的形式耦合到非定常雷诺平均Navier-Stokes 方程。为将涡量与激励关联起来，引入二维涡量输运方程，对同一分离剪切层，分析并比较了两种激励下的涡量输运特性，得到了以下结论：

1）在激励施加时，两种激励均引起了前缘激励处边界涡量的变化，对于AC-DBD 激励，体积力项是主要的涡量源；对于NS-DBD 激励，斜压项是主要的涡量源。

2）通过分析AC-DBD 激励诱导涡量的变化和展向涡结构的发展，提出了提升前缘AC-DBD 激励控制效果的反向激励方法。

3）激励关闭后，边界涡量通过黏性扩散和流动分离进入流体内部。在激励施加后1 ms 时，前缘上翼面附近逐渐形成展向涡结构；在激励施加后2 ms 时，发现两种激励对应的涡量输运方程各项中主要的成分均是对流项，区别最大的是斜压项，其次是斜黏项，且这种区别随着时间的推移逐渐弱化。分析认为两种激励对下游涡量输运影响的区别在于：NSDBD 激励后残留的热引起了流体密度梯度和机械应力（黏性应力和压力）梯度的不平行。