非精确Newton 方法中线性迭代收敛判据研究

2023-03-01冯选燕燕振国朱华君马燕凯冯新龙

空气动力学学报 2023年12期

冯选燕，燕振国，朱华君，马燕凯，冯新龙

(1.新疆大学数学与系统科学学院，乌鲁木齐 830000；2.空天飞行空气动力科学与技术全国重点实验室，绵阳 621000)

0 引言

非线性问题广泛存在于各类学科和实际问题中，是科学研究中的难点之一[1]。其高效数值求解方法的研究不仅在计算数学基础理论上具有重要意义，而且在科学与工程计算中处于重要地位，能够促进计算流体力学（Computational Fluid Dynamics, CFD）等科学研究和工程应用的发展。

具体到CFD 领域，其控制方程（Navier-Stokes equations，即N-S 方程组）具有高度非线性特征，对于绝大部分实际流动问题，往往只能对控制方程进行离散求解，为了获得全离散方程，需要同时进行空间离散和时间离散。通常的空间离散包括限差分法、有限体积法和间断有限元（discontinuous Galerkin-finite element method, DG-FEM）等数值方法[2-4]，时间离散则通常被划分为显式和隐式两类[5]。其中隐式时间推进方法是解决CFD 刚性流动模拟效率问题的重要手段[6]，然而隐式时间离散后不可避免地需要求解非线性离散系统。发展这类大型非线性离散系统的基础理论和高效求解方法是提高CFD 计算效率的关键手段[7]。

Newton 法是求解非线性方程的常用方法之一，其二阶的收敛效率在高效CFD 计算中十分具有吸引力[8]。然而传统的Newton 法需要计算非线性残差方程的Jacobian（雅可比）矩阵来构造线性迭代方程组，并且要求对线性方程组进行精确求解，上述两点在大规模CFD 计算中都是较难实现的。为了避免上述困难，通常会在上述两个环节引入近似。例如，CFD 中常用的Jacobian-free Newton-Krylov（JFNK）方法就采用有限差分来近似Jacobian 矩阵，引入了Jacobian 矩阵计算误差[9-11]；而线化后的方程组系统通常采用迭代方法进行求解，迭代方法会引入线性迭代误差[12-13]。所以CFD 等大型模拟中实际上采用的是非精确Newton 方法[14]。

对于非精确Newton 方法，国内外开展了近似方法的系列研究工作。Vanden 和Orkwis[15]讨论了精确和数值Jacobian 矩阵的求解过程及其对计算的影响，数值测试结果表明：在这两种情况下获得了较一致的迭代收敛次数及相近的收敛残差，并指出对于较为复杂的非线性系统，数值Jacobian 矩阵可能更具有优势。Ezertas[16]等在此基础上进一步研究了数值Jacobian 矩阵计算中误差的来源，探究并给出了使得有限差分近似误差最小化的有限差分扰动幅值。测试发现：在该条件下，采用数值Jacobian 矩阵表现出了与精确Jacobian 矩阵相当的收敛性能。基于此，数值Jacobian 矩阵具有实现简单等优势，被广泛应用于CFD 大规模数值模拟中。然而，Yang 等[17]的数值测试结果表明：采用无矩阵（Jacobian-free, JF）方法的数值Jacobian 矩阵并不能获得与精确Jacobian 矩阵相当的收敛特性，有限差分误差的引入会对迭代的收敛过程产生明显的影响。

另外，非精确Newton 方法在每一步的内迭代中通过线性迭代收敛判据来控制求解线性方程组时解的精确程度，在此过程中会产生迭代的收敛误差。对于该问题，文献[18]将其称为Newton 迭代的强制项，其中强制项控制系数 ηk的取值大小对收敛性有很大的影响。一些学者[19]结合理论分析和数值测试给出了该参数的不同选取方式，并给出了强制项能够保证Newton 方法二阶收敛速度的理论分析。然而，在考虑Jacobian 矩阵误差的情况下，线性迭代收敛判据的选取方式尚未得到深入研究，需要进一步考虑Jacobian矩阵误差的影响并展开对比研究。

因此，本文重点对存在Jacobian 矩阵误差情况下不同线性迭代收敛判据的表现进行了研究，分析了不同线性迭代判据所引起的过度求解问题。结合两种类型的判据发展了一种新的线性迭代收敛判据，并利用数值测试对新提出线性迭代收敛判据的优势进行了验证。

对于本文所关心的CFD 问题，其求解的Euler（欧拉）和N-S 方程，可以描述为以下形式：

1 控制方程和数值方法

1.1 隐式时间推进方法

对于Euler 或N-S 方程，式（3）是非线性方程组。采用Newton 方法对该方程进行线性化后迭代求解，迭代式为：

其中，J(Q)是残差向量N(Q)的 Jacobian 矩阵，ΔQn=Qn+1 −Qn。

为了增强计算的稳定性，通常会在式（4）左端添加伪时间项，此时不考虑时间项的计算精度，时间离散通常采用实现简单、存储量小的Euler 隐式格式，此时迭代方程变为：

式（5）中时间步长 Δt→∞时，退化为式（4）的形式。

1.2 Newton-Krylov 方法

Newton-Krylov 方法[20]目前是CFD 领域常用的大型非线性方程组求解算法，基于Krylov 空间，其具体形式为：

该类方法在Krylov 空间内构造正交的基向量，并在该空间中寻找使得线性方程组误差最小的数值解，因此有残差单调下降等优势。其收敛速度依赖于线性方程组系数矩阵的条件数（由矩阵的特征值分布决定），当矩阵的条件数较小时，Krylov 方法可以在几次搜索内将残差降到很小的量级。这里为了求解Euler 和N-S 方程产生的非对称系统，采用广义最小残差法（generalized minimum residual，GMRES）[21-22]，具体如下：

其中：M代表最大内迭代次数， σ为GMRES 迭代的收敛判据。Jqi的计算可采用有限差分近似得到，具体形式在本文1.3 节中详细介绍。N代表GMRES 的最大重启次数，重启可以有效避免存储过多Krylov 空间向量，减少正交化操作，是大规模计算中常用的技术。

而采用Krylov 方法求解线性方程组时带来的线性迭代误差，主要依赖于线性迭代收敛判据：

其中， ΔQk=Qk+1−Qk； σ可控制线性迭代的求解精度，当其取值过大时，较大的线性迭代误差可能对Newton 迭代的收敛造成较大影响，而取值过小又容易导致过度求解，造成计算浪费，因此 σ的选择对于发展高效的数值方法来说是十分重要的。

1.3 线性化方法及其误差

在每一步Newton 迭代的过程中，需要采取直接法或迭代法求解由Jacobian 矩阵J组成的线性方程组。在标准的Newton 方法中需要采用精确方法计算J，然而对于大规模CFD 计算而言，计算精确的雅可比矩阵所产生的计算量和存储量都是较大的。因此，历史上提出了多种近似雅可比矩阵方法，其中一种是对雅可比矩阵的表达式进行近似，例如在经典的LUSGS 方法中对流通量和黏性通量的Jacobain 矩阵分别采用一阶精度近似和黏性谱半径近似[5]；另外一种方法则是采用数值方法计算Jacobian 矩阵，例如CFD中常用的JF 方法就是采用有限差分方法近似Jacobian 矩阵；此外，还存在上述两种近似的混合方法[11]。本文主要讨论采用JF 方法的误差及其影响。

在构造Krylov 子空间（式6）过程中，令q=Jj−1r(k)，则Jq的计算可采用有限差分近似计算Jacobian 矩阵与向量的乘积：

2 误差影响研究

本文考虑的非精确Newton 迭代法在求解大型非线性方程组时相对精确Newton 方法存在两类误差：Jacobian 矩阵误差和线性迭代误差。这里首先给出存在两种误差情况下非精确Newton 方法的迭代式，其次给出了两种误差对Newton 迭代式的影响，最后分析了Jacobian 矩阵误差来源验证及其影响。

2.1 误差及其分析

非精确Newton 迭代的过程中，Jacobian 矩阵误差和线性迭代误差都对整个非线性方程组求解过程中的收敛性造成一定影响。对于经典Newton 法，解的迭代式为：

作为示例，这里给出Euler 方程采用DG 方法离散后的具体离散形式和Jacobian 矩阵的形式，详细矩阵系数和N-S 方程的离散形式参照文献[11]。具体残差形式为：

这里d为空间维数，M=BTΛ(wJ)B为质量矩阵， Λ为对角矩阵，D j为第j个方向的微分矩阵，B为从求解点或者模态系数到通量点的变换矩阵、BΓ为到单元边界上的通量点的变换矩阵，w和J分别代表数值积分权重和网格变换Jacobian，Mc为单元边界基函数 ϕΓ和基函数 ϕ之间的映射矩阵，F^n为对流数值通量。

其中，空间残差项N(Q) 关于守恒变量Q求导的Jacobian 矩阵J(Qn)形式：

∂L(Qn)/∂Q具有块结构，例如 ∂Le1(Qn)/∂Qe2代表第e1行和第e2列的块Jacobian 矩阵元素，其含义为第e1个单元的 L 对第e2个单元的Q的Jacobian 矩阵块。其具体形式为：

2.2 Jacobian 矩阵误差来源验证及其影响

本小节首先简单验证了采用有限差分近似的Jacobian 矩阵的相对误差变化规律，验证了Jacobian矩阵误差主要来源于差分格式带来的截断误差和计算机的舍入误差[16]，而且表明在特定的数据精度和计算格式下，都存在一个使得误差最小的ε，即最优ε，如图1 所示。图中FD 表示一阶前向差分，CD 表示二阶中心差分。

图1 数值Jacobian 矩阵的相对误差变化规律Fig.1 Relative error variations of the numerical Jacobian matrices

为进一步测试Jacobian 矩阵误差对收敛速度的影响，这里利用周期计算域内的一维Euler 系统所搭建的简单模型问题进行研究，此处选取120 个网格点，通过控制网格拉伸比使得网格向计算域两侧汇聚，并通过控制计算网格的大小比值来控制问题的刚性，此处网格拉伸比为1.05。空间离散采用一阶迎风格式，该模型问题Jacobian 矩阵的条件数约为1 ×108。图2 中，横坐标（Non-Iter）代表非线性迭代次数，结果验证了当数值Jacobian 矩阵近似误差较大时会引起效率降低甚至无法收敛的问题[16-17]，然而当Jacobian矩阵误差较小时则可能避免上述问题。

图2 不同量级Jacobian 矩阵误差对非精确Newton 迭代的影响Fig.2 Influence of the Jacobian matrix error order on the inexact Newton iteration

3 线性迭代收敛判据研究

对于Newton 类非线性系统求解方法，线性迭代误差虽然不影响计算最终收敛后的精度，但是对非线性系统能否收敛以及收敛时的计算效率有较大的影响。其中，相关研究[18]给出的线性系统迭代收敛判据的选取准则要求，在保证Newton 方法二阶收敛效率的前提下尽量避免线性系统的过度求解。所谓过度求解就是当线性系统的求解精度达到一定程度以后，继续提升线性系统的求解精度将无法显著提升非线性系统的收敛效率，此时额外增加的线性系统迭代步数就造成了线性系统的过度求解。从提高计算效率角度，避免过度求解显然是必须考虑的问题。

常用的迭代误差收敛判据有两种，一种是绝对量型收敛判据，即选取某个绝对的数值作为迭代收敛的判据，为了使得该策略中的参数更具有普适性，本文采用如下的形式：

另外一种是相对型收敛判据，即将线性系统的迭代收敛判据与非线性系统的残差进行关联，其形式如下：

此处 ηk为线性系统收敛判据的主要控制参数，其含义为线性系统迭代误差要相对当前的非线性系统残差小 ηk倍以上。文献[19]对式（20）的线性迭代收敛判据进行了较系统的研究，并从能够保持Newton 方法二阶收敛效率的角度给出了相应的数学证明和数值测试；然而并未对式（19）的绝对量型收敛判据和存在Jacobian 矩阵误差情况下式（20）的迭代收敛误差的影响开展研究。

3.1 不同 ηk的对比研究

这里采用风雷高精度软件平台[24]开展测试研究。控制方程采用N-S 方程，算例为黏性NACA 0012翼型流动问题，来流Ma=0.1，雷诺数取100，攻角为0。，翼型表面采用无滑移边界条件，计算区域采用20 倍翼型长度，在外边界采用远场边界条件。采用2842个四边形网格对计算域进行离散，如图3 所示。在当前的定常计算中，添加了伪时间项来控制线性系统的刚性以增强计算的稳定性，计算结果如图4 所示。本计算主要关注残差的收敛过程。

图3 NACA 0012 算例的计算网格分布Fig.3 Computational grid distribution for the case of NACA 0012

图4 NACA 0012 算例计算结果密度分布Fig.4 Density distribution for the flow around NACA 0012

如图5 所示，首先对比测试了 ηk分别取1×10−3、1×10−4和1×10−6情况下采用式（8）的数值Jacobian 矩阵（JF1）的迭代收敛情况，作为对比，本文同时给出了采用精确Jacobian 的结果（JF0）。从线性迭代步数（Iter）上来讲，显然采用更小的 ηk所需的线性迭代步数显著增加，线性方程组的求解精度相应提升。然而除了 ηk=1×10−3以外，所有非线性系统残差基本完全重叠；当 ηk=1×10−3时，收敛曲线在收敛初段和最终阶段已经出现了较明显的偏差。上述结果表明，当ηk≤1 ×10−4时线性迭代已经足够精确，继续降低 ηk则会造成过度求解问题，使计算效率降低。

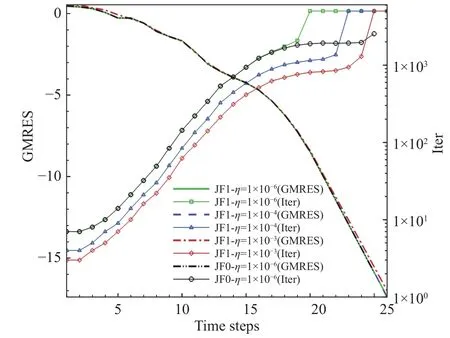
图5 NACA 0012 算例在不同Jacobian 矩阵下非线性迭代残差和GMRES 迭代步数对比Fig.5 Comparison of the nonlinear iterative residual and GMRES iteration steps for different Jacobian matrices in the case of NACA 0012

另外需要强调的是，在迭代接近收敛时，基于ηk的迭代收敛判据都会造成过度求解问题。本文进一步通过增加GMRES 的迭代重启次数来增加允许的最大线性系统迭代总步数，从而进一步研究造成上述问题的原因，结果如图6 所示。在迭代的最终收敛阶段，无论将允许的最大线性系统迭代步数增大到多大（在本文的测试范围内），线性方程组均无法收敛到 ηk=1×10−6，相应的线性方程迭代的总步数达到允许的最大值。与之相反，采用精确Jacobian 矩阵的计算结果，虽然在收敛的最终阶段迭代步数同样增加，但是并不存在上述现象，说明上述问题是当所要求的线性系统迭代误差太小时，Jacobian 矩阵误差会造成线性系统无法收敛引起的。然而从非线性系统的残差角度来看，各条曲线是基本重合的，进一步说明采用近似Jacobian 所增加的线性系统迭代是由于收敛判据过严引起的过度求解，需要发展更加合理的迭代收敛判据避免上述问题。

图6 不同GMRES 允许的最大迭代步数下的线性迭代次数Fig.6 Linear iterative number under different allowable maximum GMRES iteration steps

3.2 不同 ζk的对比研究

类似3.1 节，这里对式（19）的收敛判据进行测试，结果如图7 所示。本文分别给出了 ζk取1×10−6、1×10−10、1×10−14的测试结果，为了对比，图中同时给出了 ηk=1×10−6情况下的收敛曲线。可以看到，采用ζk类型的迭代收敛判据，只有在 ζk取很小的值时才能保证迭代收敛。但是，当 ζk取值很小时（如1×10−14），在迭代的初始阶段会造成较严重的过度求解现象。而在迭代接近收敛的阶段，采用 ζk类型的迭代收敛判据却可以较好地避免过度求解的问题。

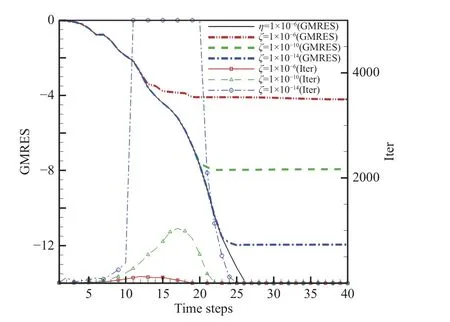
图7 NACA 0012 算例中不同ζ 取值情况下非线性迭代残差和GMRES 迭代步数对比Fig.7 Comparison of the nonlinear iterative residual and GMRES iteration steps for different ζ in the case of NACA 0012

3.3 一种新的线性迭代收敛判据

基于以上研究结果，本文发展了一种新的迭代收敛判据：

其中 max函数内两项分别为式（19）和式（20）对应的绝对收敛判据和相对收敛判据，这里取两项中的较大值。在非线性迭代初期||N(Qk)||2较大，因此ηk||N(Qk)||2的量级会大于ζk||Q0||2，从而避免了后者在非线性迭代初期所引起的严重过度求解问题；随着迭代逐渐接近收敛， ||N(Qk)||2逐渐减小，只要取合理的参数，可以使得 max函数在接近收敛时取 ζk||Q0||2，此时可以有效避免图5 中的过度求解问题。在此基础上，本文还在 max函数外添加了相应的 min函数，其作用是保证每个线性迭代至少要下降一定量级（本文中取ηmin=0.01），从而避免类似图7 中迭代不能完全收敛的问题。本文中 ζk取1×10−13，主要从计算的舍入误差角度进行选取，由于最终线性迭代误差会加到Qk上， ζk=1×10−13的参数选择可以避免线性方程组收敛到比Newton 迭代步本身舍入误差更小的量级，从而避免类似图5 中的过度求解问题。

图8 同样采用NACA 0012 算例对不同迭代收敛判据进行了对比，直至迭代第19 步采用式（21）的新迭代收敛判据（NewTol）得到了与 ηk=1×10−6完全相同的计算结果。此后采用 ηk=1×10−6的线性迭代步数迅速增加到允许的最大值，线性迭代无法收敛，而采用式（21）的线性迭代步数则开始下降，说明如设计的那样，式（21）中 ζk||Q0||2部分开始发挥作用从而大幅减少了线性迭代的计算量。直至第23 步（残差收敛至1×10−13）时采用新判据的非线性系统残差依然与ηk=1×10−6重叠，随后采用式（21）的线性迭代步数开始显著减小，非线性残差曲线不再重叠。表1 给出了残差收敛到不同量级时所需要的线性迭代总步数，该指标能够很好地反映出所消耗的总计算量。当残差收敛到1×10−10以下时，JF0- ηk=1×10−6（精确Jacobian、ηk=1×10−6）、JF1- ηk=1×10−6（近似Jacobian、 ηk=1×10−6）和JF1-NewTol（近似Jacobian、新判据）所需线性迭代步数分别为13113、19670 和12692 步；当残差收敛到1×10−13以下时，所需线性迭代步数分别为16964、29670和13870 步；当残差收敛到1×10−16以下时，所需线性迭代步数分别为21473、44670 和15453 步。可以看到，新发展的线性迭代收敛判据能够有效避免过度求解的问题，显著降低所需要的线性系统迭代步数。线性迭代步数最多降低3 倍，从而提高计算效率。

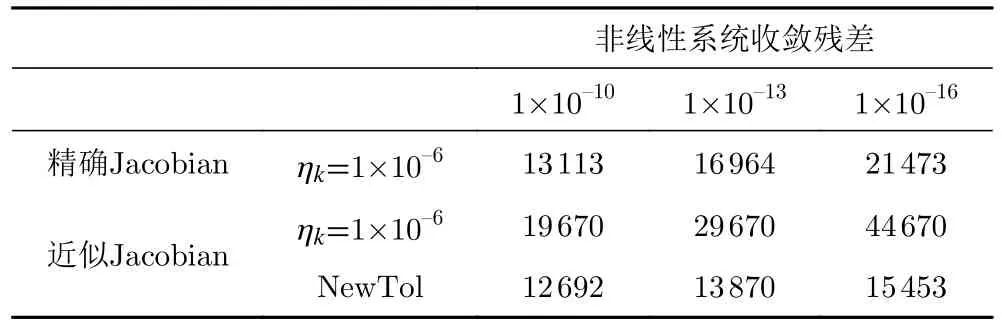
表1 不同判据情况下迭代收敛所需线性迭代步数对比Table 1 Comparison of the linear iteration steps under different convergence criteria

图8 新线性迭代收敛判据的残差和迭代步数Fig.8 Nonlinear iterative residual and GMRES iteration steps for the new linear iteration convergence criterion

为了进一步验证上述迭代收敛策略在不同计算状态中的通用性，本文通过改变离散格式的计算精度来改变非线性系统的特性和规模。将DG 格式的计算精度提高到三阶，此时总共求解的网格自由度变为17052 个。图9 给出了三阶精度的计算结果，可以看到，采用新的线性迭代收敛判据同样能够很好地避免接近收敛状态下的过度求解问题，从而显著提高计算效率。

图9 三阶DG 格式计算中新线性迭代收敛判据的残差和迭代步数Fig.9 Nonlinear iterative residual and GMRES iteration steps for the new linear iteration convergence criterion with third-order DG scheme