基于深度置信网络与多目标粒子群算法的通用飞机机翼优化设计

2023-03-01吴涌钏

空气动力学学报 2023年12期

吴涌钏，孙刚，陶俊

(复旦大学航空航天系，上海 200433)

0 引言

通用飞机是民用航空工业中重要的组成部分，在工业、农业、林业等领域有重要的应用，在医疗卫生、抢险救灾、气象探测等方面也有不可替代的作用。升力的提升可以提高通用飞机的载货量、载油量，从而提升飞机的整体性能，因此，升力的优化对通用飞机的设计有重要意义。

国内外研究人员对机翼的设计进行了大量的研究。Benaouali[1]应用代理模型方法对ONERA M6 进行机翼外形优化。马晓永[2]应用集成序列二次规划（sequential quadratic programming, SQP）优化算法对NAX880 V2.0 轻中型高速涡扇公务机机翼进行多点优化设计研究。周志强[3]开展了基于遗传算法的飞机机翼结构拓扑优化设计方法研究。郝璇[4]采用雷诺平均N-S（Reynolds average Navier-Stokes, RANS）方程实现阻力的精确求解并建立响应面模型，对不同升力系数、马赫数的多个飞行状态进行变弯度减阻优化。

对于传统的机翼优化设计问题，如果在优化过程的每步迭代中都通过CFD 数值模拟来评估目标函数，会消耗大量的计算资源。为了提高优化效率，减少资源的消耗，可以使用代理模型取代CFD 在优化中的计算过程。反向传播（back propagation, BP）神经网络[5]是一种由误差反向传播算法训练得到的多层前馈神经网络，是当前被应用最广泛的神经网络模型之一。吕小龙等[6]利用本征正交分解（proper orthogonal decomposition, POD）提取本征向量，并使用径向基函数（radical basis function, RBF）方法进行插值，建立了具有较好反演精度和泛化性能的PODRBF 代理模型。此外，还有一种Kriging 模型[7]，是依据协方差函数对随机过程/随机场进行空间建模和预测（插值）的回归算法。

在机翼的优化问题中，优化变量往往是高维数据，如果用原数据去进行训练和优化，则会造成较大的计算资源消耗，增加计算时间成本。因此，许多研究会采用数据降维方法对原数据进行处理。独立分量分析（independent component analysis, ICA）[8]基于信息理论，是使用最广泛的降维技术之一，可用于将多元信号分离为加性子分量。POD[9]则可以把多维随机过程进行低维近似描述并提取复杂随机过程的本质特征，从而达到数据降维的目的，可用于外形气动设计。线性识别分析（linear discriminant analysis,LDA）[10]使用统计学、模式识别和机器学习方法，在两类物体或事件的特征中找到一个线性组合，从而能够特征化或区分它们，所得的组合可用来为后续的分类做降维处理。

飞机通常在多个工况下飞行，这就使得机翼的气动优化成为多目标、多约束问题。多目标多约束问题的求解依赖优化算法，为此，许多研究人员对优化算法进行了研究。多目标遗传算法（multi-objective genetic algorithm, MOGA）[11]是一种模拟大自然中生物体进化规律的自然选择和遗传学机理的生物进化过程的计算模型，对于一个优化问题，使一定数量候选解（个体）的抽象表示（染色体）的种群向更好的解进化。模拟退火算法（simulated annealing, SA）[12-13]的思想来源于热力学中对固体退火过程的模拟，其将温度T模拟为控制参数，将内能模拟为目标函数值f，对于控制参数T的每一个取值，算法持续进行“产生—新解—判断—接受或舍弃”的迭代过程，并逐步衰减T值，算法终止时的当前解记为所得近似最优解。多目标蚁群算法（multi-objective ant colony optimization, MOACO）[14-15]是模拟蚂蚁的觅食行为与旅行商问题（traveling salesman problem，TSP）的相似性提出的，用蚂蚁的路径表示待优化问题的可行解，路径较短的蚂蚁释放的信息素量较多，随着时间的推进，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也愈来愈多，最终蚁群集中到最优路径，即优化问题的最优解。

综上所述，机翼在多工况下的空气动力学优化作为一个多目标、多约束的问题，具有重要意义。本文提出了一种基于深度置信网络代理模型和多目标粒子群算法的多目标优化框架。首先，利用基于型函数/类函数变换参数化方法（class function/shape function transformation, CST）得到的几何参数，利用CFD 模拟得到空气动力参数，然后对机翼的几何参数进行主成分分析（principal component analysis, PCA）降维处理，建立起机翼的数据库，在此基础上训练深度置信网络（deep belief network, DBN）代理模型，以准确预测机翼的气动参数；其次，通过将优化算法与代理模型耦合，建立起多目标粒子群优化框架；最后，通过该框架对机翼进行多工况下的气动优化，在不增加其阻力系数的情况下提升其升力系数。

1 数值模拟方法与验证

1.1 RANS 方法

通过求解RANS方程，可得到机翼的气动参数：

数值模拟中，空间离散采用Roe-FDS[16]方法，时间推进采用隐式LU-SGS[16]方法，湍流模型为方程SA （Spalart-Allmaras）[17]湍流模型。

1.2 算例验证

为了验证RANS 方法的精准度和可靠性，使用DLR翼身组合体进行验证，图1 展示了该翼身组合体的网格结构，网格单元数为6.34 × 106。

图1 DLR-F6 翼身组合体网格Fig.1 Grid of DLR-F6 wing-body assembly

数值模拟计算结果如表1 所示。可以看出，数值模拟计算结果与实验所得结果误差较小，说明RANS 具有较高的精确度。

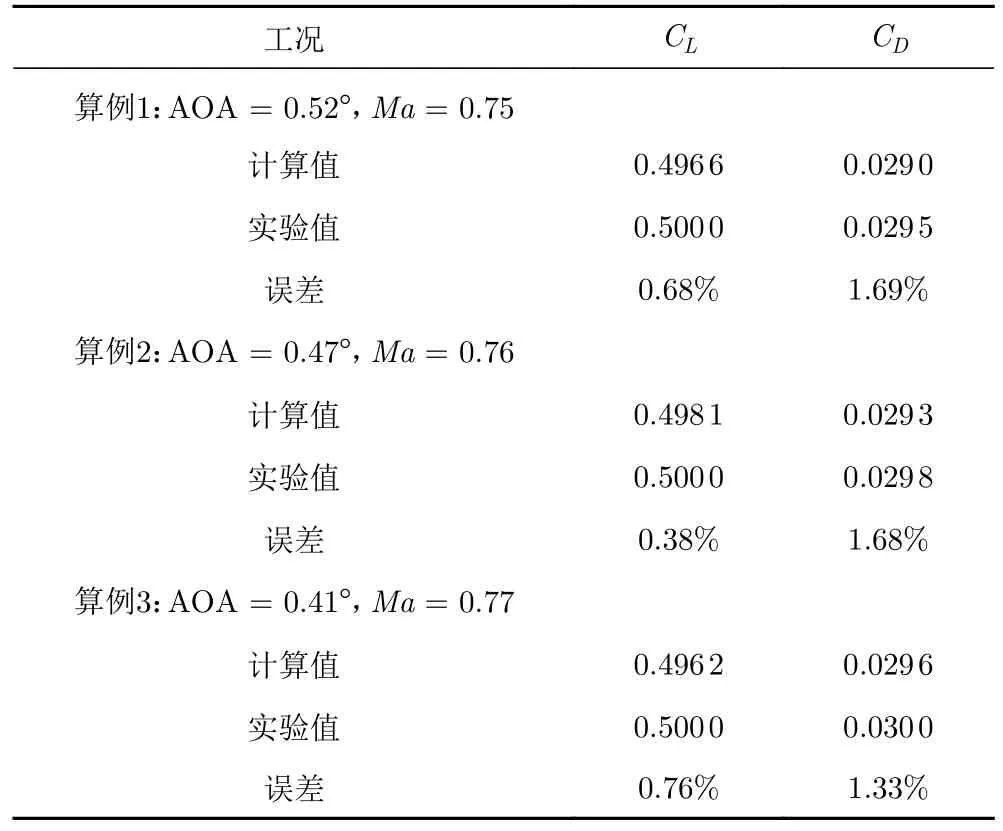
表1 DLR-F6 翼身组合体的数值模拟结果(Re = 3.0 × 106)Table 1 Numerical simulation results of the DLR-F6 wing-bodyassembly(Re = 3.0 × 106)

在对机翼进行优化时，需要对机翼的几何数据进行处理，用尽量少的特征参数描述机翼的几何特征，以降低计算量，同时必须具有足够高的精度，以确保参数对几何特性描述的准确性及计算的可信度。

本研究所优化的机翼半翼展长为8.305 m，翼根弦长为2.180 m，翼梢弦长为0.910 m。选取机翼在翼根、翼尖梢以及1/2 半展长处的剖面翼型（分别记为剖面翼型1、剖面翼型2、剖面翼型3），以其几何数据作为机翼的几何数据。图2 为机翼的平面形状图，图3 为选取的三个剖面的示意图。

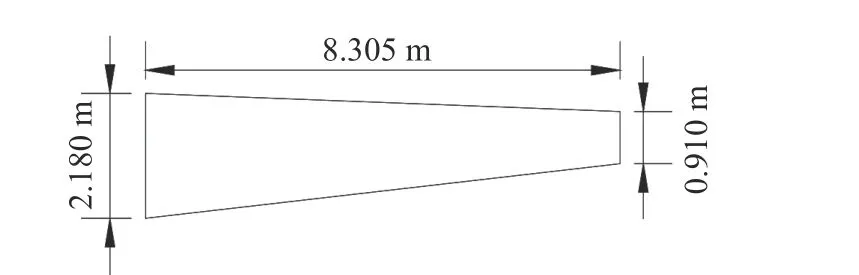
图2 机翼的平面形状示意图Fig.2 Schematic figure of the plane shape of the wing

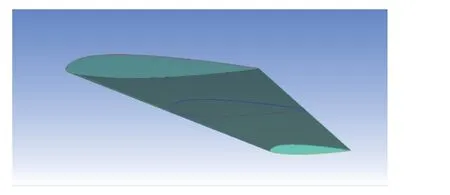
图3 机翼三个剖面的示意图Fig.3 Schematic figure of the three sections of the wing

图4 原翼型曲线和CST 拟合翼型曲线Fig.4 Original airfoil curve and CST fitted airfoil curve

图5 CST 参数化拟合翼型残差Fig.5 Fitting residuals of the CST parameterized airfoil

使用CST 参数化方法[18]处理几何数据。CST 方法是一种用类别函数和形状函数表示翼型几何形状的参数化方法。类别函数表示的是要描述的几何体的类型，形状函数是在类别函数的基础上对几何特性进行修正。翼型用CST 参数化方法进行表示的公式如下：

2 优化问题

2.1 CST 参数化

型与原始翼型基本一致，残差均小于1×10−2，说明采用的CST 方法在描述翼型几何形状方面具有很高的可靠性。经过CST 参数化后，机翼的几何特性可以用42 个参数表示。

2.2 PCA（主成分分析）

参数化后的机翼几何参数有42 个变量，这对于后续的代理模型训练以及优化过程是偏高的，容易造成较大的计算资源损耗。为了让计算更加高效便捷，对数据进行降维处理。

PCA[19]是一种基础的数据降维方法，其作用是用较少的变量来代替较多的变量，并反映出原来多个变量的大部分信息，被广泛应用在数据分析、机器学习等方面。

原机翼包含了3 个翼型的几何数据，每个翼型数据为14 维，共42 维。现对每一个翼型进行PCA 降维处理，当每个翼型取前10 个主成分时，累计贡献率分别达到了93.9%、93.4%、94.04%，则可以认为处理后所得的30 维机翼几何数据包含了绝大多数原机翼的数据。图6 展示了三个剖面翼型的14 维参数贡献率。

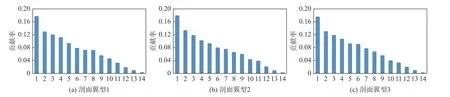
图6 3 个剖面翼型的14 维参数的贡献率Fig.6 Contribution rates of the 14 dimensional parameters of the three airfoils

2.3 优化问题描述

本研究要优化的是机翼在多种工作状态下的升力系数。选取其在马赫数为0.4 时的状态作为优化工况1，在马赫数为0.45 时的状态作为优化工况2，迎角均为4°，工况1 和工况2 的雷诺数分别为Re1=9.83 × 106和Re2= 1.11 × 107。

基于5 套网格对原机翼开展了网格无关性验证，5 套网格单元数分别为2.0 × 106、2.5 × 106、3.0 × 106、3.5 × 106、4.0 × 106，计算结果如表2 所示，其中，各参数的下标1 和2 分别对应工况1 和工况2。由计算结果可得，伴随网格数增长，计算结果呈收敛趋势，从计算精度和计算资源考虑，选用网格单元为3.5 ×106的网格作为计算网格，网格如图7 所示。

表2 原机翼气动参数在不同网格数量下计算结果Table 2 Simulation results of aerodynamic parameters oforiginal wing under different numbers of grids

图7 机翼的网格Fig.7 Grid of the wing

以两种工况下的机翼升力系数作为优化目标，约束条件为优化后机翼阻力系数小于或等于原机翼阻力系数。优化问题可以描述为：

3 优化方法

3.1 深度置信网络

本研究使用的代理模型DBN[20]是一种概率生成模型，这种模型通过训练调整神经元之间的权重，可以用来进行数据生成，常用于回归分析、类型识别等。

深度置信网络的基本构成元件是受限玻尔兹曼机（restricted Boltzmann machines, RBM）[21]，其典型网络结构如图8 所示。一个RBM 由两层神经元构成，一层是可视层，由可视神经元组成，用于数据的输入；一层是隐藏层，由隐藏神经元组成，用于特征检测。RBM 两层神经元之间对称连接，同层之间的神经元相互独立。

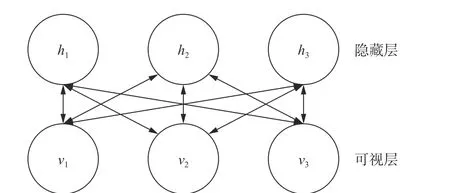
图8 RBM 结构Fig.8 Structure of RBM

对于输入样本X=(x1,x2, ···,xn)，隐藏神经元开启的概率为P(hi=1)=1/(1+e−wx)，从0 ～ 1 的均匀分布中抽取一个随机值，与开启概率进行比较，决定该神经元是否开启。经过预训练，可求得最佳的权重值，使得其产生训练样本的概率最大。

将多层RBM 进行串联，以上一层RBM 的隐藏层作为下一层RBM 的可视层，在最后一层加上softmax 分类器，即形成了深度置信网络。这种网络将RBM 的训练作为神经网络的预训练，在最后一层加入BP 算法。深度置信网络典型结构如图9 所示。

图9 DBN 结构Fig.9 Structure of DBN

3.2 改进多目标粒子群优化算法

粒子群优化（particle swarm optimization, PSO）算法[22]是一种通过模拟鸟群捕食行为设计的优化算法。假设区域里只有一块食物（即优化问题中的最优解），鸟群的任务是找到这个食物源。在整个搜索过程中，群体中的鸟会互相传递位置信息，判断是否找到了食物源（最优解），同时将食物源（最优解）的信息传递给整个鸟群，最后，整个鸟群可以收敛在食物源周围。

把鸟个体简化为一个粒子，把粒子的位置作为目标问题的候选解，把候选解对应的目标函数值作为适应度，把粒子群中适应度最高/最低的粒子位置作为群体最优位置，把单个粒子历史适应度最高的位置作为粒子历史最优位置，粒子的飞行过程即对应个体的搜索过程。粒子的飞行速度以粒子历史最优位置和群体最优位置为参考进行调整，此即为进化迭代过程。经过多轮迭代，可以求出问题的最优解。粒子的速度和位置的进化方程如下:

多目标粒子群优化（multi-objective particle swarm optimization, MOPSO）[23]算法旨在将只能用于单个对象的粒子群算法（PSO）应用于多目标。在其基础上，Raquel[24]将粒子拥挤距离、储存非支配解的仓库等引入其中，来提高粒子群的多样性。拥挤距离是估计一个解周围其他解的密度的参数。对于每个目标函数，根据目标函数的值对外部精英解集中的解进行分类，然后计算与每个解相邻的两个粒子形成的立方体的平均边长，如图10 所示，计算的结果就是该解的拥挤距离，粒子的拥挤距离可以反映解的多样性。该种算法即为拥挤距离多目标粒子群优化（crowding distance multi-objective particle swarm optimization,CDMOPSO）算法[25]。

图10 拥挤距离示意图Fig.10 Schematic figure of the crowding distance

为了提高收敛速度和全局搜索能力，引入了αstable 函数族[26]来改进标准的MOPSO 算法。在αstable 函数族中，稳定系数α是描述分布状态的一个重要参数，它决定了所生成的随机数的分布范围。图11 显示了不同α值下的α-stable 分布。通过引入α-stable 分布，MOPSO 在迭代过程中生成随机数，使粒子进行突变，避免过早陷入局部最优。该种算法即为α-stable 多目标粒子群优化（α-stable multi-objective particle swarm optimization, ASMOPSO）算法。多目标粒子群算法如图12 所示。

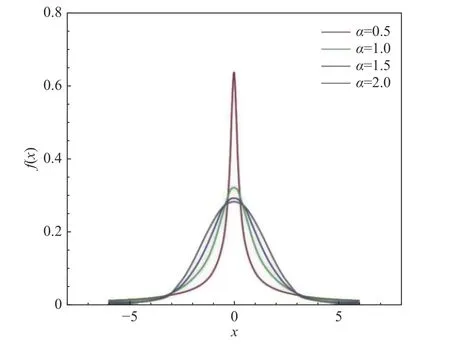
图11 不同α 值下的α-stable 分布示意图Fig.11 Schematic figure of the α-stable distribution under different α

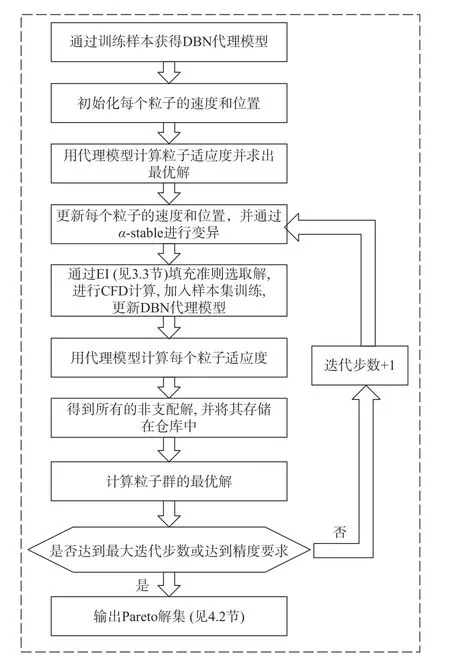
图12 MOPSO 结构Fig.12 Structure of MOPSO

为了比较CDMOPSO 和ASMOPSO 的性能，采用目标函数ZDT3 进行测试。利用反世代距离（inverted generation distance, IGD）[27]对算法的性能进行了综合评价。IGD 不仅可以评估多目标解集的收敛性，还可以评估解集的分布特性，见式（5）：

d(o,P) 是近似解集P中的个体与精确解集P*中的个体o之间的最小欧氏距离。该算法得到的最优解集用p表示。IGD 的值越低，优化结果越好，算法的性能也越好。ZDT3 函数可以描述为：

x是一个30 维变量，其范围为[0，1]，n= 30。ZDT3 由CDMOPSO 算法和ASMOPSO 算法独立评估30 次。IGD 值的统计数据如表3 所示，可以看出ASMOPSO 的IGD 值明显低于CDMOPSO，因此ASMOPSO 算法的性能优于CDMOPSO 算法。

表3 CDMOPSO 和ASMOPSO 算法所得IGD 的比较Table 3 Comparison of IGD values between the CDMOPSOalgorithm and ASMOPSO algorithm

3.3 EI 加点准则

在优化过程中，每次迭代均采用期望改进（expected improvement, EI）[28]加点准则对代理模型进行更新。将EI 作为代理优化的适应度函数，在每次迭代中将EI 最大的点添加到样本中，在每次迭代中更新代理模型。多目标EI 的定义为

在每次迭代中，选择EI 最大的点进行CFD 数值模拟，获得空气动力学参数，添加到样本中，并更新替代模型。

4 计算结果与分析

4.1 代理模型训练结果

基于原机翼的CST 参数，通过拉丁超立方采样方法（latin hypercube sampling, LHS）[29]，在原机翼参数[0.8, 1.2]的倍数范围内，生成980 组CST 参数，并通过数值模拟获得一个包含980 个机翼的几何参数和气动参数的数据库。

DBN 由4 层RBM 组成，以几何参数为输入、气动参数为输出进行训练。预训练后，初始化权值，将最后一层RBM 的输出作为最后两层BP 神经网络的输入。

在数据库中选取882 个机翼作为训练样本，98 个机翼作为测试样本，将样本输入模型进行训练，得到的代理模型记为代理模型1。在数据库中随机选取450 个机翼作为训练样本，50 个机翼作为测试样本，为了降低后续的训练和优化计算量，对机翼几何数据进行PCA 降维处理，降维后的几何参数为30 维，将PCA 降维处理后的样本输入模型进行训练，得到的代理模型记为代理模型2。

图13 为DBN 代理模型的训练结果，其中Y为期望输出，T为DBN 输出。可以看出，代理模型1 的相关系数R为0.995 16，代理模型2 的相关系数R为0.974 02，均接近于1，两个模型都取得了较为精确的结果。

图13 DBN 代理模型的训练结果Fig.13 Training results of the DBN surrogate model

图14 和图15 分别展示了测试样本的计算值与训练所得代理模型预测值的对比。从图中可看出，绝大多数预测值与计算值基本吻合。

图14 机翼气动参数代理模型1 的预测值与计算值Fig.14 Surrogate model 1 prediction values and calculation values of the aerodynamic parameters of wings

图15 机翼气动参数代理模型2 的预测值与计算值Fig.15 Surrogate model 2 prediction values and calculation values of the aerodynamic parameters of wings

DBN 模型预测的升力系数和阻力系数的平均误差如表4 所示。由表可以看出，代理模型1 的升力系数与阻力系数的平均误差小于1%，代理模型2 平均误差小于2%，说明DBN 模型的预测具有较高的精度。代理模型1 的误差明显小于代理模型2，由此可得，代理模型1 具有更高的精准度，原因是代理模型1 的训练样本更多且保留了更多原数据的信息。

表4 升力系数和阻力系数的平均预测误差Table 4 Average prediction errors of the lift coefficients and thedrag coefficients

4.2 多目标粒子群优化结果

将训练得到的无PCA 处理和有PCA 处理的代理模型嵌入多目标粒子群优化算法中，分别记为优化1 和优化2。

将粒子数设置为500，Pareto 解数设置为10，突变率设置为0.8。优化的终止条件是最近10 代的适应度值的最大差异均小于0.01%。在每次迭代中，如果满足终止准则，则优化结束，否则迭代将继续。

优化1 与优化2 分别经过91 步与102 步迭代后，收敛得到最优解。优化1 与优化2 的优化过程对比如图16 所示，优化得到的Pareto 解集如图17 所示。

图16 优化1 与优化2 的优化过程Fig.16 Optimization process with/without PCA processing

图17 优化1 与优化2 优化所得Pareto 解集Fig.17 Pareto solution set obtained by optimization with/without PCA processing

为了在每次迭代的Pareto 解集中选出一个最优解，现定义一个函数：

其中ω1、ω2是权重系数，在此处设为[0.5，0.5]。对Pareto 解集中的所有解计算出对应的fop值，fop值最大的解即为满意解。

4.3 优化结果验证

优化后机翼的几何模型如图18 所示。

图18 优化机翼的几何模型Fig.18 Geometric model of the optimized wing

对优化机翼进行数值模拟，得出优化后机翼在工况1 与工况2 下的升力和阻力系数计算值。原机翼和优化机翼的气动参数在DBN 模型下的预测值及计算值如表5 所示。

表5 原机翼与优化机翼气动参数的预测值与计算值Table 5 Prediction and calculation values of aerodynamicparameters of the original and optimized wings

由表可以看出，优化1 得到的优化机翼较原翼型的升力系数在工况1 下提升9.81%、工况2 下提升10.14%，阻力系数在工况1 下减少1.04%、工况2 下减少0.20%；优化2 得到的优化机翼较原翼型的升力系数在工况1 下提升9.44%、工况2 下提升9.71%，具有较明显提升，阻力系数在工况1 下减少0.69%、工况2 下不变，优化效果较为理想。

可以看到，优化1 与优化2 的优化结果基本相近，为了进一步比较两种优化的效率，表6 给出了以无代理模型时过程需要100 步迭代达到收敛计算，优化1、优化2 和无代理模型三种情况下的计算算例数量和计算时间。