基于离散等价方程的滑移壁面边界约束算法

魏雁昕，刘 君

(大连理工大学 航空航天学院，大连 116024)

0 引 言

计算流体力学（Computational Fluid Dynamics, CFD）的实质是求解偏微分方程的初边值问题。尽管实际物理流动千变万化，但是在很多问题的计算中原始方程是相同的，数值模拟得到的流场差异源自空间形状或初场不同。CFD 应用于定常流动情况时，收敛的数值解与初始条件无关，在流动方程已经确定的情况下，决定流场特性的主要因素是边界的求解方法。从CFD 发展的早期开始，许多学者针对有限差分法的边界条件进行了广泛的研究[1-4]。针对外流场模拟的空气动力学问题，两类边界条件起着至关重要的作用：一类称之为无反射边界条件，用于计算亚声速远场边界；另一类则为无穿透边界条件，用于处理壁面边界。对于远场边界，通常使用特征变量方法得到远场特征边界条件[5]或者基于特征线相容关系得到远场Riemann 边界条件[6]。远场边界距离物体较远时（如对于翼型计算，最小距离通常取10 倍弦长），使用上述两种方法求解亚声速远场边界均可得到满意的计算结果，因此不作为本文的研究内容。而物面边界的计算决定了近壁面附近的流场特性，直接影响物体气动力/热预测的准确性。

本文针对有限差分法的滑移壁面边界条件开展研究，以二维欧拉方程为例，在壁面处存在4 个未知的流动变量，只有法向无穿透条件是准确已知的，即vn=0，其余3 个物理量无法直接给出。CFD 早期的边界处理是基于双曲方程的特征理论，将边界约束带入原始方程，把边界条件的影响作为源项处理，推导出针对此类边界的修正方程，通过求解修正后的控制方程得到边界状态[3]。因为修正后的控制方程难以写成守恒形式，边界节点和内点的离散格式不相容，降低了计算的稳定性，也不利于软件的工程化应用，所以此类方法使用较少。随着CFD 的发展，目前壁面边界条件通常有两种不同的施加方式：在每个计算步内直接修正边界节点的值，该方法称为强边界条件；或者在边界节点处建立差分方程，通过计算边界节点通量更新边界节点状态，该方法称为弱边界条件。强边界条件利用边界附近内部流场节点信息，通过外推插值等方式获得边界面的节点物理量。常用的强边界条件包括压力外推边界和特征边界[7-8]。弱边界条件则需要在节点上建立差分方程，本文依据离散方式的不同将弱边界条件分为两类：一类是基于流场内侧信息，在法向方向构造单侧差分格式进行求解[9]，该方法没有对法向速度进行限制，因此无法严格保持物面无穿透的强制条件；另一类主流处理方法是将计算区域进行拓展，在物体内部设置虚拟节点，通过补充模板的方式将边界节点作为内点进行求解。由于虚拟节点不是实际存在的，因此该方法的关键在于如何提高虚拟节点参数的合理性。最为常用的是基于“反射原理”提出的镜像法（symmetry technique, ST）[7]，该方法将内部节点参数按照镜面对称的方式构造虚拟节点参数。此外，Dadone 等[10]在壁面附近引入旋涡流动假设模型，提出一种通过熵和总焓对称分布假设构造虚拟节点的曲率修正对称技术（curvature-corrected symmetry technique, CCST）。该方法使用局部动量方程获得虚拟节点压力，在此过程中引入了物体曲率的影响，可以更加真实地反映壁面附近的压力和速度分布，CCST 基于格心型有限体积方法提出[10-11]，逐渐被推广至高阶谱方法[12]。近年来，在贴体网格基础上，CCST 方法也被应用于浸没边界法的边界计算中，称之为虚拟体单元法（ghost body-cell method, GBCM）[13-14]，不过，目前还未见该方法应用于贴体网格有限差分法的相关报告。

调研文献发现，当前研究中所有使用虚拟节点的物面边界方法在确定虚拟节点过程中仅考虑了法向相邻节点的影响，即仅使用流场内侧法向节点信息构造虚拟节点参数，并没有考虑壁面切向相邻节点的影响。本文基于上述认识，在壁面节点上建立满足边界条件的约束方程，将虚拟节点参数表示为计算模板中法向和切向相邻节点的函数，通过求解约束方程得到满足边界约束的虚拟节点参数。该方法中虚拟节点受壁面切向节点的影响，可以有效体现边界曲率对流动的影响，算例的对比验证表明：该方法具有良好的计算精度，可以有效降低近边界附近的数值误差。

1 传统滑移壁面求解方法

1.1 压力外推边界条件

压力外推是CFD 中最为常用的一类强边界条件，文中用PI-n表 示，其中n为插值多项式阶数。该方法在壁面处满足法向动量方程，建立(∂p/∂n)|wall=0的假设模型，使用单侧迎风格式对上述压力梯度进行离散，通过多项式插值得到边界节点压力值。壁面法向速度强制为零，切向速度使用内侧参数外插得到，再依据等熵条件确定壁面节点密度[7,15]。以二维问题中MUSCL（ monotone upstream-centered schemes for conservation laws）五点格式为例，壁面速度由式（1）确定，这种处理方式本质上是通过内点外推边界值，在内侧区域流场梯度变化较大的情况下，高阶的外插算法容易导致边界值“过冲”[10]。

式中：下标 (i,0)表 示壁面边界节点信息， (i,1)和(i,2)则 为流场内侧节点参数， n表示壁面节点处的单位法向矢量。此外，当使用高阶格式，如五阶WENO（weighted essentially non-oscillatory）等时，在边界区域常采用不同于内部节点的格式进行计算。一种处理方法是基于单边差分的边界格式，在边界内侧节点处进行降阶处理，使用三阶迎风WENO/ENO 计算内侧节点数值通量，边界节点同样使用内部节点压力外推确定，该方法的具体内容参见文献[15]。

1.2 虚拟节点边界条件

弱边界条件需要在边界节点处建立差分方程，通过计算节点通量的方式对壁面参数进行更新。由于缺少计算模板，通常在计算区域外设置虚拟节点，采用补充模板的方式将边界节点当作内部节点处理，边界约束通过虚拟节点参数体现。最为常用的方法为ST，根据镜面对称原则确定虚拟节点的参数，如式（2～3）所示：

其中： ρgj、pgj和vgj分别为第j个虚拟节点的密度、压力和速度矢量，j为垂直壁面方向的节点编号。使用反射技术构造虚拟节点的处理方式，壁面无穿透的条件是弱施加的，当式（2）和式（3）应用于无曲率平直壁面时，可以严格满足法向无穿透条件，在物体存在曲率的条件下，镜像对称的处理方式会引入较大误差，并且无法保证壁面节点的法向速度恒等于零。

2 滑移壁面边界约束算法

调研文献认识到，在现有基于虚拟节点的弱边界方法中，虚拟节点的变量是直接由内侧法向节点通过镜像或者外推插值确定的。当该种方法应用于包含曲率的壁面边界时，在计算边界节点通量过程中，切向速度和法向速度不能完全解耦，即切向方向通量分裂后会产生非零的法向动量通量。因此，即便在计算初始时刻强制壁面法向速度vn=0，经过时间推进后也会导致vn≠0。本文方法以严格满足壁面无穿透条件为出发点，增加法向速度随时间导数 ∂vn/∂t=0的强制约束，保证离散方程在时间推进过程中严格满足vn=0的边界条件。按照上述思路构造的边界算法兼顾弱边界和强边界条件的优点：与弱边界算法一样，边界和内部节点使用统一的离散格式；同时与强边界算法一样，壁面数值解可以严格满足vn=0的强制条件。

需要说明的是，有限差分法应用于包含曲率的壁面边界的贴体网格时需要进行坐标变换，将控制方程由笛卡尔坐标系变换至计算坐标系后再进行格式离散。在此过程中容易引入坐标变换诱导误差，文献[16]中使用多种类型网格进行自由流保持测试，表明该诱导误差广泛存在于差分格式计算中。本文重点在于求解存在弯曲的滑移壁面边界，因此，在对边界条件进行对比研究前需要先消除坐标变换引入的诱导误差。本文采用刘君提出的离散等价方程及其离散 准 则（discrete equivalence equation and its discrete rule，DEER）[17]，以坐标变换后得到的包含非零源项的控制方程为原始方程，按照与差分格式相同的准则离散对流项和坐标变换源项。公式推导和算例验证表明：DEER 方法可以在任意扰动网格上实现自由流保持，消除了坐标变换引入的诱导误差。DEER 方法的详细推导参见文献[17-20]。

笛卡尔坐标 (t,x,y)下二维守恒型Euler 方程：

上式中守恒变量和对流通量表示为：

求解过程中需要将方程从笛卡尔坐标系 (t,x,y)变换到计算空间 ( τ,ξ,η)，因此实际应用差分格式离散的是计算空间上包含源项S的控制方程：

本文不涉及网格运动，因此仅给出静止网格条件下表达形式：

按照DEER 算法要求，对流项和坐标变换产生的源项需要使用相同差分格式离散，将式（15）合并可以得到滑移壁面的边界约束方程：

1）对于无黏流动，假设虚拟节点 −η与内部节点η存在总焓相等条件：

3）根据内部节点 η=1的法向速度方向，分别使用两种模型对虚拟节点的切向速度进行计算，如图1 所示，其中黑色箭头方向为 η=1节点处的速度方向。

图1 切向速度假设模型示意图Fig.1 Sketch of wall tangential velocity

图2 DEEB 方法求解流程图Fig.2 Flow chart of DEEB method

（1）将 η=1节点处法向速度方向指向流场内部的流动定义为切向速度模型一，使用多项式插值得到虚拟节点的切向速度：

其中s为计算模板中法向方向已知节点个数，cj为多项式插值系数。对于一阶迎风格式，s=2，则虚拟节点的切向速度表示为：

（2）将 η=1节点处法向速度方向指向壁面的流动定义为切向速度模型二，此时在壁面附近可能存在激波，高阶的外推插值可能会导致过冲，在这种情况下，将切向速度进行镜像处理，表示为：

需要说明的是，式（19）和式（21）是在壁面存在曲率条件下设立的假设模型，对于平直壁面，无论内点η=1处法向速度方向正负，都直接使用式（21）确定虚拟节点切向速度，此时本文方法等价于传统的镜像方法。本文边界算法在曲线坐标系下的原始方程是离散等价方程，将壁面无穿透条件表示为时间导数恒为零的约束方程，因此，称其为“基于离散等价方程的约束边界算法（discrete equivalent equation with boundary constraint algorithm，DEEB）”。

在二维问题中，每个虚拟节点需要确定四个参数，使用一阶迎风格式时，通过式（16～19）或式（21）即可获得虚拟节点的参数。由于约束方程式（16）与离散格式和通量分裂格式相关，无法给出统一的显式表达式，本文使用弦截法求解该非线性方程。对于二阶或者高阶格式，为了确定更多的虚拟节点参数（二阶需要两个虚拟节点，五阶WENO 需要三个虚拟节点），需要补充压力递推条件。在无黏流动中，壁面边界本质上是一条贴壁流动的流线，可以利用计算模板中的内部节点多项式插值得到壁面压力的左值，同样利用虚拟节点可以插值得到壁面压力的右值：

上文介绍的DEEB 方法主要是基于网格与壁面正交的条件，然而在许多问题的模拟中，网格难以保持和壁面正交化。对于非正交网格，可以利用离散等价方程计算中仅使用当地点坐标变换系数的特点[16-17]，在壁面节点处建立局部坐标系，其中 ξ方向保持不变，构造新的 η*方向与壁面正交，如图3 所示。以空间一阶格式为例，在该局部坐标系中， η*轴与j=1的原始网格线相交于图中蓝色节点处，使用反距离加权插值[21]得到交点u∗的物理量。一阶迎风格式在二维条件下使用交点周围的5 个相邻节点进行插值，插值模板表表示为：

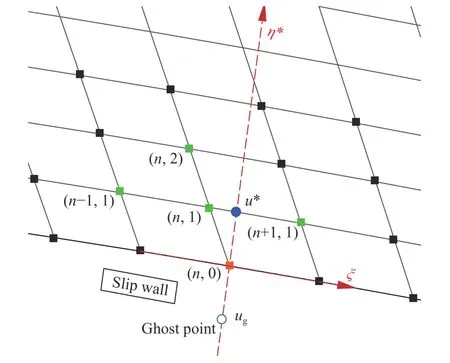
图3 非正交网格局部坐标系（一阶迎风格式）Fig.3 Local coordinate system of non-orthogonal grids (first-order upwind)

其中： Δlm表 示模板中第m个节点到交点的距离，对于高阶格式，只需要扩大插值模板即可。需要说明的是，模板中心点的选取准则是与 η*正交的原始网格线上距离交点最近的网格节点，即图3 中节点 (n,1)。综上所述，在壁面节点处构造正交的局部坐标系，然后使用式（16～19）或式（21）确定虚拟节点（空心蓝色节点）参数，后续计算流程与正交网格下完全相同。

当DEEB 方法应用于五阶WENO 等高精度格式时，拉格朗日插值多项式即使在光滑解条件下也可能存在稳定性问题[22]。本文使用Tan 等提出的WENO型插值方法，通过引入非线性权的方式确定插值模板中每个节点的贡献，再使用高阶插值得到局部正交坐标系中对应位置节点参数，该插值方法具体细节可参见文献[22]。

虽然通过求解约束方程得到的虚拟节点参数可以提高边界计算的精度，但是在这一过程中我们不希望引入过多额外的计算消耗，幸运的是，DEEB 方法仅在壁面节点处激活，且壁面节点相对于整个计算节点数量总是相对较少的。此外，随着壁面附近流场区域逐渐收敛，由于虚拟节点参数保持恒定，此时约束方程的求解停止，通过分析可知，DEEB 方法的使用不会消耗过多的计算成本。

3 算例验证

本小节以MUSCL3 格式[7]和五阶WENO-Z 格式[23]为例，对本文所提方法进行算例验证，以此考查DEEB 方法应用于不同离散格式的准确性和适用性。算例模拟中近似黎曼求解器采用Vanleer[24]格式，使用多步Rung-Kutta[25]法进行时间离散。需要说明的是，本文DEEB 方法中的约束方程是耦合在时间推进过程中的，因此可以使用现有的限制函数计算壁面附近存在激波的流动问题。由于本节算例目的在于对不同边界计算方法进行对比，为了排除限制器引入的数值耗散，因此选取了不存在激波的光滑流场进行数值模拟。

3.1 MUSCL 格式计算结果

3.1.1 二维亚声速圆柱绕流

首先使用马赫数0.38 条件下圆柱绕流问题验证DEEB 方法针对固定曲率问题的模拟能力，计算无量纲自由来流为 (ρ,u,v,p)=(1.4,0.38,0,1.0)，圆柱半径r=0.5，计算区域取10 倍圆柱直径，外边界统一使用黎曼远场边界条件。计算区域使用4 套网格进行离散，网格周向和径向节点个数分别为 40×10、 80×20、160×40和 3 20×80，将4 套网格定义为Mesh1～Mesh4。周向节点均匀分布，法向壁面附近局部加密。采用延拓网格对周向分布的周期边界进行处理，排除该边界对计算的影响。

图4 不同方法计算得到的马赫数等值线图Fig.4 Mach number contours obtained by different methods

图5 不同方法计算得到的熵增等值线图Fig.5 Entropy contours obtained by different methods

图6 中统计了不同方法的熵增误差 L1范数随网格细化的收敛曲线，N为网格节点总数，从图中可知，PI-2 方法和ST 方法由于边界处理引入了较大误差，导致全场熵增收敛精度仅为 1.360 0和 1.090 0，本文DEEB 方法通过约束方程提高虚拟节点参数的合理性，使用与内部节点相同的离散格式进行求解，虽然测试结果表明DEEB 方法并未达到MUSCL 格式的二阶设计精度，但是计算得到的误差绝对值和收敛精度均优于两种传统求解方法。DEEB 方法没有达到格式设计精度的原因可能是在边界约束方程求解中使用切向速度模型（式（19、21））和压力递推假设（式（22））作为计算补充条件，在此过程中可能引入了模型误差，这也是下一步研究中需要解决的首要问题。

图6 不同方法的熵增误差L1 范数对比Fig.6 L1 errors of entropy obtained by different methods

对于无黏亚声速圆柱绕流，攻角为0°条件下，理论上流场完全对称，因此常使用阻力系数评价计算对称性。图7 给出了4 套网格条件下使用不同方法计算得到的阻力系数，由曲线可知，随着网格加密，阻力系数逐渐收敛至网格无关解，DEEB 在Mesh3 和Mesh4 条件下阻力系数相差微小，CD值约为 0.000 4，展示了其网络收敛性较其他方法的优势。

图7 亚声速圆柱绕流阻力系数Fig.7 Grid indenpence test of the drag coefficient of a subsonic cylinder

另一方面，阻力系数为积分量，反映的是圆柱整体压力分布情况，而当局部正压力误差与局部负压力误差累加后得到的阻力值反而更小，因此认为阻力系数不能严格反映上下游压力对称性。为此，本文通过考查上下游物面网格对称点压力差进行对称性评价。压力差定义为：

如图8 所示，其中pdown为下游物面点（橘黄色节点A∗） 压力，pup为 上游物面点（绿色节点A）压力。本文计算中以上游驻点为起始点，定义顺时针方向夹角为θ ，统计 θ ∈(90°，270°)物面上（蓝色壁面）所有节点的δp值。

图8 压力对称测点示意图Fig.8 Sketch of symmetric pressure measuring points

壁面上下游节点压力差分布曲线如图9 所示，θ=180°对应下游驻点。从图中可知，DEEB 方法压力差明显小于PI-2 和ST 方法。注意到ST 方法在驻点处不对称性最为显著，最大压力差δpST,max=0.019 3，而DEEB 方法得到了最大压力差仅为δpDEEB,max=0.000 4。此外，图10 给出了收敛流场中壁面法向速度（使用来流速度进行无量纲化）分布曲线，DEEB 方法将法向动量通量为0（式（16））作为约束加入离散方程中，因此，时间推进过程中法向速度恒等于0；ST 方法存在非零的壁面法向速度，无法严格保证物面无穿透条件；PI-2 方法由于使用压力外推的强边界处理方式，在每一时间步强制壁面法向速度为0，所以与DEEB 方法得到的法向速度曲线重合。

图9 壁面上下游节点压力差分布曲线Fig.9 Pressure difference between symmetric measuring points

图10 壁面法向速度分布曲线Fig.10 Azimuthal variation of the surface wall-nomal velocity

图11 为Mesh3 对应的局部网格图，其中红色圆环所示节点为DEEB 算法激活区域，从图中可知，约束算法仅在壁面节点处使用。表1 给出了该网格条件下三种方法使用Rung-Kutta 法显式计算50 000 步所消耗的CPU 总时间Tall，其中以PI-2 方法的CPU时间为基准得到归一化时间T∗。可以看出，ST 方法和DEEB 方法由于使用虚拟节点，在边界处求解差分方程的计算成本略高于压力外推的边界方法。在本算例中节点总数为6 400，其中壁面边界节点数为160，这也是DEEB 方法求解边界约束方程需要的节点数量，仅占总数的 2.5%，因此DEEB 方法不会引入过多的计算时间，计算总时间仅为PI-2 方法的1.055倍。

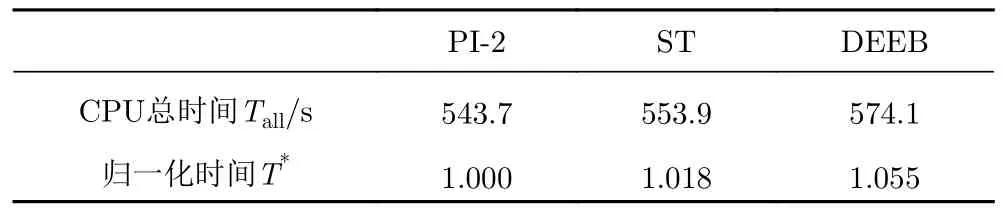
表1 二维亚声速圆柱绕流CPU 计算总时间Table 1 CPU time for simulating subsonic inviscid flows arounda 2D cylinder

图11 DEEB 算法激活区域（Mesh3）Fig.11 Activated region for DEEB method (mesh3)

3.1.2 二维平滑凸起通道内亚声速流动第二个测试算例为马赫数0.50 的自由流在平滑凸起通道内的流动[26]，来流攻角0°，用于考查DEEB 方法在任意曲率滑移壁面的模拟效果。计算网格量 200×50， 其中壁面方向设置 200个节点，竖直方向节点总数为 50。边界条件设置如图12所示，下边界为光滑凸壁面，边界形状由函数y=0.625exp(−25x2)定义，其中 −2 ≤x≤2。图13 为局部区域网格图，可以看出，下壁面凸起处网格与壁面非正交，因此可以考查本文方法在非正交网格条件下的计算效果。图14给出了3 种方法得到的下壁面法向速度曲线，DEEB 方法在非正交网格条件下依然可以满足法向无穿透条件，而ST 方法在凸起处存在较大的法向速度，无法保证壁面法向速度为零。图15 显示了3 种方法模拟得到的马赫数等值线图，除本文DEEB 方法外，其余两种方法得到的等值线在凸起下游位置处发生拐折。

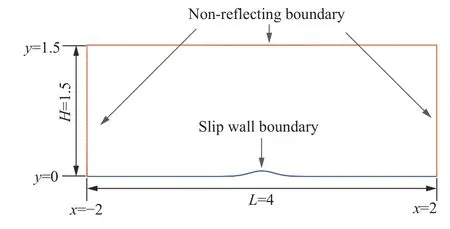
图12 二维平滑凸起通道内亚声速流动计算边界Fig.12 Sketch of the computational domain and boundary conditions

图13 局部区域网格图Fig.13 Zoom-in view of local grids

图14 下壁面法向速度曲线Fig.14 Wall-normal velocity at the slip wall

图15 不同方法模拟得到的马赫数等值线图Fig.15 Mach number contours around a smooth bump obtained by different methods

图16 给出了对应的熵增云图，从图中可以看出DEEB 方法再次得到了最小的壁面熵增，最大值仅为ΔsDEEB,max=0.000 38； PI-2 方法最大熵增为ΔsPI-2,max=0.000 73，且在凸起上游位置也存在明显熵增，表明在流场变化较为剧烈的边界处，压力外推差值会引入较大 误 差；ST 最 大 熵 增 ΔsST,max=0.002 2。本 例 和3.1.1 节测试结果均表明，在曲率滑移壁面条件下使用镜像对称的方式构造虚拟节点会严重降低计算精度。DEEB 方法通过求解约束方程得到了严格满足边界条件的虚拟节点参数，可以有效降低近边界区域的计算误差。

图16 不同方法模拟得到的熵增云图Fig.16 Entropy contours around a smooth bump obtained by different methods

3.2 五阶WENO 格式计算结果

本节使用五阶WENO-Z 格式进行离散，边界附近分别使用边界格式降阶处理和虚拟节点两种方法与DEEB 方法进行对比计算。其中，使用边界格式的处理方法对壁面节点处压力使用三阶外推，密度依据等熵关系确定[15]，速度满足法向无穿透条件，该方法表示为PI-3；补充虚拟节点的计算方法依旧使用ST 表示。

3.2.1 二维亚声速椭圆绕流

使用二维椭圆绕流对本文方法在高精度格式中的计算性能进行测试，椭圆由方程x2/4+y2/9=1确定，为了保证全场亚声速流动，自由来流马赫数Ma=0.28， 沿椭圆周向分布 1 60 个节点，沿径向分布50个节点，壁面附近网格如图17 所示。同样使用马赫数和熵增作为不同方法计算能力的评价指标，从图18 可知，DEEB 方法获得了对称性最好的马赫数轮廓，PI-3 方法在下游驻点流线上产生了非物理凸起，而ST 方法误差最大，下游位置难以形成对称分布流场。这是因为五阶WENO 格式需要构造三个虚拟节点，对于存在曲率的壁面边界，使用镜像法确定虚拟节点参数引入的误差较大，进而对每一个包含虚拟节点的子模板均产生影响，最终导致了较大的数值误差。图19 给出了椭圆后缘位置处速度矢量分布，可以看出ST 方法产生了明显的非物理涡结构，进一步说明了在高精度格式中，对存在曲率的壁面边界应尽可能避免使用镜像法进行边界计算。从熵增等值线（图20）中可以看出，DEEB 方法仅在曲率变化最大处存在微弱熵增，有效降低了边界区域的数值耗散。PI-3 方法因为对边界内侧节点进行了降阶处理，同时使用外推插值的方法确定壁面压力和速度，虽然使用了等熵假设计算壁面密度，但是熵增还是远大于DEEB 方法的模拟结果。图21 的壁面法向无量纲速度曲线显示了DEEB 方法应用于WENO 格式时依然可以严格满足法向无穿透条件。

图17 椭圆绕流局部网格图Fig.17 Grids nearby an ellipticesh grids

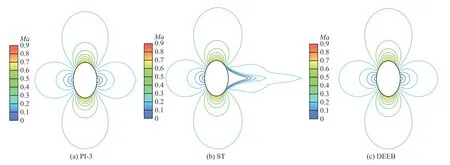
图18 椭圆绕流马赫数等值线Fig.18 Mach number contours around an elliptic

图19 椭圆后缘绕流速度矢量图Fig.19 Velocity vectors at the trailing edge

图20 椭圆后缘绕流熵增等值线Fig.20 Entropy contours around the elliptic

图21 椭圆表面法向速度曲线Fig.21 Wall-normal velocity on the elliptic surface

最后，对不同方法计算得到的阻力系数（以椭圆长轴为参考面积）进行定量对比（CD,PI−2=5.56×10−4，CD,ST=9.74×10−2，CD,DEEB=1.20×10−4），DEEB 方法计算所得阻力系数最接近理论值，而ST 方法误差最为显著，这也与马赫数等值线和熵增等值线结果相吻合，再次表明在存在曲率条件下，传统镜像法存在精度严重降低的问题。

3.2.2 Prandtl-Meyer 流动

计算模型和网格分布如图22 所示，下壁面是Ma∞=1.357的自由来流经过20°折转角形成的流线，网格线与壁面保持正交，流向和法向网格点个数为60×60，在第一道膨胀波前设置10 层均匀网格用于避免入口边界处理的影响，上边界和超声速出口边界采用外推处理。上侧边界距离壁面较远，保证膨胀波在上边界产生的误差不会影响到下壁面，无量纲来流参数为 (ρ,u,v,p)=(5.4, 20/9, 0, 31/3)。

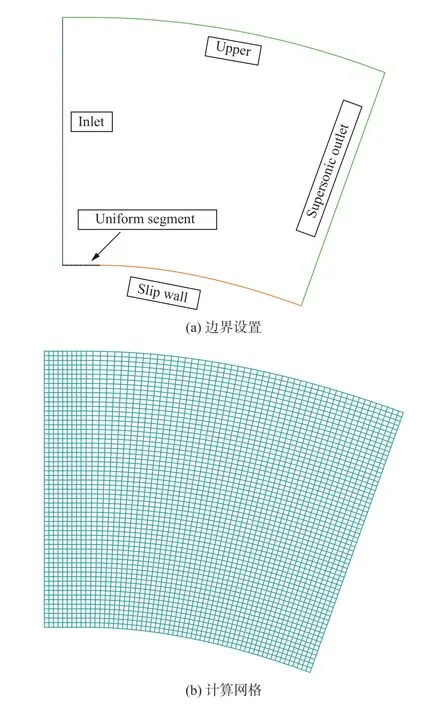
图22 计算网格和边界条件设置Fig.22 Grids and boundary conditions

图23 和图24 给出了不同方法模拟得到的流场等值线图，图中彩色等值线为计算结果，黑色等值线为相同标尺下对应的理论值。从图中可以看出，ST方法得到的计算误差最大，在壁面附近等值线存在显著的非物理弯折，而本文DEEB 方法得到的结果与理论值吻合度最高，在壁面处也可以保持等值线的平直。

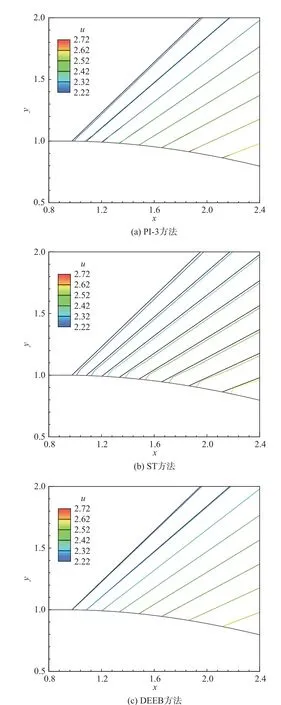
图23 不同方法计算得到的速度u 等值线图Fig.23 u contours obtained by different methods

图24 不同方法计算得到的压力等值线图Fig.24 Pressure contours obtained by different methods

以图25 为例对PI-3 方法的误差产生机理进行简要分析，在这一方法中，壁面压力和切向速度利用内部法向节点三阶外推插值获得，虽然壁面节点（红色节点）在第一道膨胀波位置处受到膨胀波的影响，但是此时内部节点（蓝色节点）位于膨胀波波前，使用内部节点外插得到的壁面节点仍然保持均匀流参数，而这与理论流场显然是不相符的，因此在膨胀波初始位置处压力外推插值的方法存在误差极值。

图25 PI-3 方法外推插值误差分析Fig.25 Extrapolation error of PI-3 method

同样的，使用图26 所示流场对ST 方法的误差机理进行分析，图中彩色等值线为压力理论值，壁面节点计算时需要补充三个虚拟节点（j=−1,−2,−3）以进行通量求解，按照传统的对称反射技术（即式（2～3））可得：

图26 ST 方法虚拟节点构造误差分析Fig.26 Ghost node construction error of ST method

Prandtl-Meyer 流动的一个显著特点是在来流参数一定的前提下，同一偏折角度对应的特征线上所有变量值均为定值，因此将图26 中特征线（理论等值线）延长至物体内部后可以对虚拟节点参数的合理性进行判定。图中结果显示j=−1节点位置处对应的理论值介于p=7.0和p=7.5两条等值线之间，即满足7＜p−1＜7.5条件。而使用传统对称方法获得的虚拟节点压力p−1=p1＞7.5， 同理j=−2和j=−3两个虚拟节点存在相同的问题，且距离壁面越远的虚拟节点误差越大，这也解释了在五阶WENO 格式中使用ST 方法的计算效果远差于MUSCL 格式的原因。

此外，通过提取沿下壁面的压力误差曲线来定量对比不同方法的计算效果，其中，压力误差定义为：

其中：pi,j为 压力的数值解，pei,j是 对应节点的压力理论值，图27 显示了不同方法壁面处压力误差曲线，可以看出所有方法在第一道膨胀波附近都存在较大误差。分析认为此处流场由均匀流开始膨胀，虽然流场参数保持连续，但是参数的导数存在间断，因此会导致误差极值。本文DEEB 方法在此处的最大误差仅为0.001 6，远小于PI-3 方法和ST 方法的压力误差。此外，图28 给出了壁面节点的法向速度曲线，DEEB 方法虽然使用了虚拟节点，但是因为约束方程的作用，依旧可以保证法向无穿透的强制约束条件。上述等值线图和压力曲线分析表明：DEEB 方法可以直接应用于五阶WENO 格式，通过求解约束方程获得的虚拟节点参数更为合理，边界节点使用与内部相同的离散格式，可以在满足边界约束的前提下，有效提高壁面附近流场计算的准确性。

图27 壁面压力误差曲线Fig.27 Relative error of the wall pressure

图28 壁面法向速度曲线Fig.28 Surface wall-normal velocity

4 结 论

本文以壁面无穿透条件为约束准则，在构造虚拟节点过程中引入了壁面相邻切向节点的影响，通过求解约束方程获得了合理的虚拟节点参数。在此基础上，提出了一种面向有限差分方法的无黏流动边界算法，该方法既能保证数值解严格满足无穿透条件，又能在边界点使用与内点完全相同的离散格式。通过亚声速和超声速算例模拟验证了本文方法的准确性：

1）首先，针对MUSCL 格式开展数值模拟，通过亚声速圆柱绕流算例与传统计算方法进行对比，发现DEEB 方法能够使在圆柱下游处马赫数和压力等物理量对称性得到明显改善，近边界区域的熵增也显著减小。

2）其次，使用平滑凸起通道内的亚声速流动算例考查了本文方法在任意曲率壁面边界条件下的模拟能力。

3）最后，通过椭圆绕流和存在解析解的Prandtl-Meyer 流动对本文方法在WENO 格式下的适用性进行了验证。数值结果表明：DEEB 方法可以有效改善传统虚拟节点方法误差较大、无法满足壁面无穿透的缺点，降低边界计算引入的数值误差。

本文工作为有限差分格式的物面边界求解提供了一种新的思路，当前研究仅针对无黏流动和壁面处仅存在法向速度约束的情况，后续将对边界约束方程进行推广，开展针对黏性物面的边界算法研究，相关工作目前正在进行中。