基于改进黑猩猩算法的弹药装填轨迹规划

徐达，王兆阳，李华，王小闯，曹振地

(陆军装甲兵学院 兵器与控制系，北京 100072)

当今世界战争形式随着科技发展而变化，智能化战争正在来临，以无人车为代表的无人化装备已经走上战场。世界上越来越多国家的军队注重于军用无人系统技术方案的研究。在现有设备无法满足需求的情况下，为应对战争形式发展，无人作战平台需要一款智能化弹药装填机器人完成大口径火炮装填工作[1-3]。而装弹效率是弹药装填机器人的核心问题之一，对弹药装填机器人进行时间最优轨迹规划具有重要研究意义。

弹药装填机器人时间最优轨迹规划可分为两个阶段[4]，首先用插值算法对机器人轨迹进行拟合，其次通过智能优化算法对机器人的运动时间进行优化。在机器人时间最优轨迹规划方面有许多学者进行了相关研究。郑昱等[5]通过构造脉动连续轨迹曲线，使用插值时间变量代替系数变量，并采用粒子群优化算法优化关节轨迹。汪婷等[6]提出了一种六轴机械臂时间最优轨迹规划方法，在满足机械臂运动学及动力学约束情况下，使用五次多项式对机械臂关节角进行描述，采用GA-DE-SQP优化算法对机械臂轨迹规划进行时间优化。陈波等[7]基于3次样条插值理论，通过罚函数法，建立时间最优数学模型,提出双种群粒子群算法优化适应度函数。

Elias[8]提出了一种超冗余机械臂时间最优轨迹规划方法，使用标准多种群遗传算法优化了机械臂的运行时间。郭鑫鑫等[9]通过3-5-3多项式进行插值并使用改进型萤火虫算法进行了时间最优轨迹规划。王延年等[10]通过改进后的PSO算法对轨迹进行优化，改进后的PSO算法能快速准确地收敛到最优解。蔡永超[11]通过结合膜计算与粒子群算法，提出了膜计算-粒子群算法，将多种粒子群算法的优势融合在一起，达到了提高搜索精度和收敛速度的目的，将此算法应用于机械臂关节空间轨迹规划，减少了机械臂运行时间，提高了机械臂运行效率。

笔者提出一种改进黑猩猩算法，并将所提的算法与标准黑猩猩优化算法、粒子群算法和灰狼优化算法进行对比；在一定的约束条件下，对弹药装填机器人经3-5-3分段多项式插值得到的轨迹进行时间最优化。

1 问题描述

1.1 多项式插值

笔者采用3-5-3分段多项式插值进行弹药装填机器人轨迹规划，将弹药装填机器人抓弹轨迹分为3段，由起始点M0、中间点M1、中间点M2和终止点M3共4个插值点分割，每1段的曲线函数可表示为

(1)

为保证轨迹连续平滑，给出约束条件：

(2)

(3)

(4)

对曲线函数系数求解，有

(5)

b=[0 0 0 0 0 0x30 0x00 0x2x1],

(6)

a=A-1b=[A1A2A3],

(7)

(8)

将系数代入式(1)中，可得对应函数表达式。

1.2 目标函数

弹药装填机器人从抓弹位置到放弹位置的时间即为工作时间，由各个时间段总和而成，时间最优化就是对各个时间段进行优化，提高装弹效率。定义目标函数:

f(t)=∑(t1+t2+t3).

(9)

根据弹药装填实际要求，只对角速度进行约束：

max{|Vi|}≤Vmax，i=1,2,3.

(10)

式中：Vi为每个时间段内的角速度；Vmax为极限速度。

2 时间最优规划

2.1 黑猩猩优化算法

黑猩猩优化算法是由Khishe和Mosavi等于2020年提出的一种启发式优化算法，主要模拟了黑猩猩对于猎物的攻击、驱赶、拦截和追逐4种社会行为[12]。其拥有最重要的两大特点：一是将种群划分成独立个体，模拟其狩猎时的分工行为，而个体的多样性可以使算法更加彻底地搜索空间以提高算法的勘探能力；二是引入混沌因子来代表黑猩猩在围猎过程中受到群体激励而带来的个体混乱捕猎行为，从而提高了算法在开发阶段的收敛速度[13]。

在自然界的黑猩猩群体中，黑猩猩因能力不同而分为Attacker、Barrier、Chaser和Driver。在黑猩猩群体狩猎过程中，黑猩猩们按照身份完成不同的工作。在狩猎成功后，黑猩猩可以用猎物换取性行为等好处。因此，在获取一定量的食物后黑猩猩忘记自己的身份，此时会出现混乱影响群体狩猎。

黑猩猩优化算法的基本过程如下：假设有N只黑猩猩，第i只黑猩猩的位置为xi，群体最优解为XAttacker，次优解为XBarrier，第三最优解为XChaser，第四最优解为XDriver。

1)追逐猎物。黑猩猩接近猎物的位置更新公式如下:

(11)

式中：d为黑猩猩与猎物间的距离；Xprey为猎物位置；Xchimp为黑猩猩位置；a、m、c为参数。

2)攻击阶段。此阶段黑猩猩寻找猎物位置，然后进行合围。攻击通常由Attacker完成，Barrier、Chaser和Driver只参与狩猎。在算法中4种身份的黑猩猩分别更新位置，其他黑猩猩根据四者位置进行更新：

(12)

式中：D为各类型黑猩猩与猎物间的距离；X为猎物位置；X(t+1)为其他黑猩猩位置；A、m、C为参数。

2.2 改进黑猩猩算法

黑猩猩算法也存在容易陷入局部最优等启发式算法普遍存在的缺点，但其收敛精度和收敛速度具有优势。

2.2.1 混沌映射

将混沌映射与智能优化算法相结合，利用混沌序列的遍历性、随机性和快速发散性等特点，得到更高效率的算法[14-15]。

笔者采用Logistic映射对种群初始化，增加种群多样性，使初始解更均匀。

Zk+1=μZk(1-Zk),

(13)

式中，Zk∉{0, 0.25,0.5,0.75,1},μ∈[0,4]。

采用Piecewise映射生成m因子，强化黑猩猩群体社会动机，避免陷入局部最优。

(14)

式中：P∈(0,1)为控制参数；Xk∈(0,1)。

2.2.2 适应度加权位置更新

由位置公式(12)可知，黑猩猩群体中的其他黑猩猩是根据当前Attacker、Barrier、Chaser、Driver的位置来更新其位置，可以看出在标准黑猩猩算法中，因为位置更新公式容易陷入局部最优，所以引入适应度加权进行位置更新。

(15)

fh=fa+fb+fc+fd

,

式中，fa、fb、fc、fd分别为Attacker、Barrier、Chaser、Driver当前的适应度。针对弹药装填机器人时间最优轨迹规划，对最大速度进行约束，避免出现适应度函数输出为0的情况。

2.3 算法步骤

笔者提出的基于改进黑猩猩算法的机器人时间最优轨迹优化方法主要步骤如下：

步骤1设置种群规模N、最大迭代数次数tmax、收敛因子f、混沌因子m和影响系数A、C等基本参数。

步骤2利用Logistic混沌映射初始化位置。

步骤3对目标函数进行求解，进行超速判定选择；计算个体适应度，确定群体最优解为XAttcker，次优解为XBarrier，第3最优解为XChaser，第4最优解为XDriver。

步骤4更新A、C，按照式(12)更新位置。

步骤5判断是否到达最大迭代次数，达到即满足终止条件，输出XAttcker，否则返回步骤3。

2.4 算法比较

选用标准黑猩猩优化算法(Chimp)、灰狼优化算法(GWO)和粒子群优化算法(PSO)等算法，通过表1所示的6个测试函数与改进黑猩猩优化算法(WChimp)进行对比，验证WChimp算法在寻优精度、收敛速度和稳定性方面的优越性。

表1 基准测试函数

选取6个不同类型的测试函数测试WChimp算法的性能，结果如图1所示，其理论最优值都为0，前3个函数为单模态测试函数，后3个为多模态测试函数。通过最优值、平均值和标准差检验算法的收敛精度、收敛速度、全局探索能力和稳定性。通过图1可以直观地看到算法的收敛速度和最优解的值。改进算法在收敛速度方面具有明显优势，取得最优解的值在质量方面表现良好。

测试时，每个算法在每个测试函数分别独立重复20次，得到最优值、平均值和标准差，结果如表2所示，分别测试算法的寻优能力、收敛精度与稳定性。通过表2可以看出，WChimp算法相比用于其他算法更接近理论最优值，在函数f1,f2,f5和f6中都得到理论最优值，体现了WChimp算法良好的寻优性。从20次独立重复的运算后得到的标准差来看，WChimp算法在6个测试函数中都表现最优，取得最小标准差，体现了WChimp算法良好的稳定性。

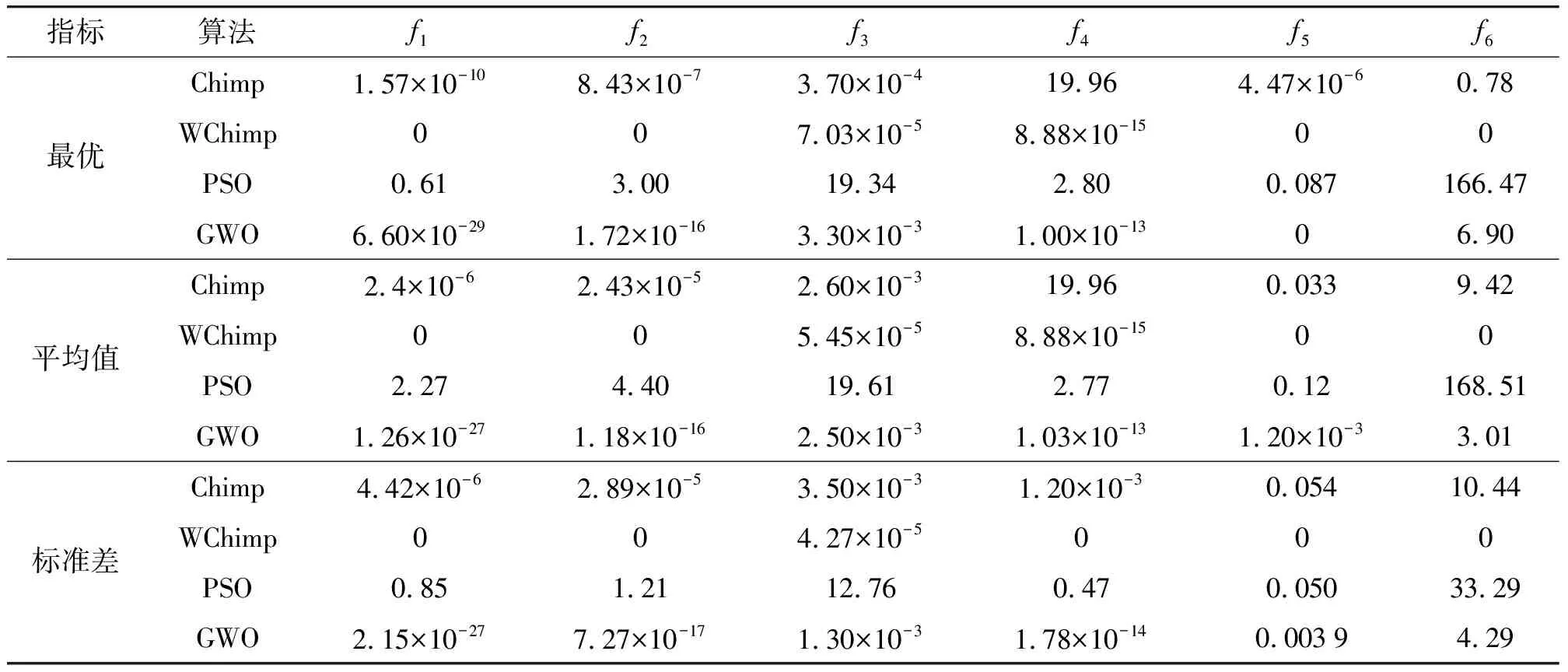
表2 基准测试函数优化结果

3 优化与仿真

对六自由度弹药装填机器人展开研究，设置黑猩猩种群数量30，空间维度为3，最大迭代数为300，假设时间总和为12 s，初始化黑猩猩位置，机器人关节最大运行角速度为170(°)/s，初始速度和终止速度都为0 rad/s、初始加速度和终止加速度都为0 rad/s2。选取4个路径点后通过逆运动学求出关节空间插值点，如表3所示。

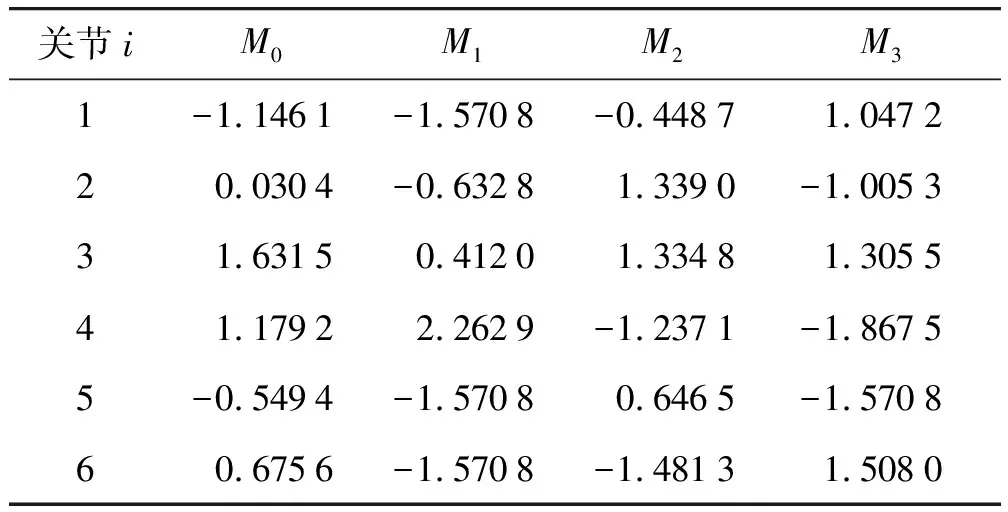
表3 机械臂关节空间插值点 rad

经过时间优化，利用 MATLAB 得到6个关节的位置p、速度v以及加速度a曲线，结果如图2所示。由图2可知，经过改进算法优化后，运行时间取各个关节所需时间最大值为8.83 s。各关节位置曲线变化平滑，易于完成弹药装填工作；各关节速度曲线起点与终点都为0 rad/s，表明初始速度与终止速度都为0 rad/s，且都满足约束条件；各关节加速度曲线起点与终点都为0 rad/s2，表明初始加速度与终止加速度都为0 rad/s2，满足约束条件。

4 结束语

笔者以弹药装填机器人为研究对象，在一定的约束条件下对其关节空间3-5-3多项式插值轨迹规划运用改进黑猩猩算法进行了优化。通过与其他算法对比验证了改进黑猩猩算法的有效性与优越性，在收敛精度、收敛速度和稳定性等方面具有良好表现。通过仿真得到机器人位置、速度及加速度曲线，满足约束条件，缩短了机器人完成弹药装填的时间，提高了弹药装填效率，为弹药装填机器人轨迹规划提供帮助。