开孔迫击炮内弹道与后坐阻力匹配性研究

2023-03-01张晋杰李强谭庆

火炮发射与控制学报 2023年1期

张晋杰，李强，谭庆

(1.中北大学机电工程学院，山西太原 030051；2.湖南国防工业职业技术学院，湖南湘潭 411207)

中小口径迫击炮具有弹道弯曲、死区小、威力大、射速快、质量轻、结构简单和造价低等特点，所以即使在现代战争中也有其不可替代的作用[1]。在战争形式日益变化的现代，迫击炮则会越来越向着增强独立作战能力及人工智能化方向发展[2]。

传统迫击炮采用人工装填，需要士兵计算读取射表后对附加药包质量进行增减和调节射角等操作，以实现对范围目标的完整覆盖，操作较为繁琐。如若在身管上开一可变大小的泄气孔，亦可改变迫击炮的内弹道诸元，并实现初速分级。美国陆军装备发展与战备司令部哈里·戴蒙德实验室的相关研究[3]可以说明这一方法是可行的。

而对于前冲击发式自动迫击炮国内已有不少相关研究[4-7]，但由于其制退复进机的结构参数相对固定，所以现有的前冲击发式自动迫击炮并不能像传统迫击炮一样通过增减装药量实现变初速发射。

文献[8]提出了一种新型摩擦阻尼缓冲器，并以某小口径自动炮为研究对象，分析了不同射速和不同摩擦阻尼缓冲器条件下炮身所受的后坐力大小。文献[9]提出了一种由电磁阀控制的摩擦阻尼式可变后坐力的软后座控制系统。

笔者综合前人的研究成果，设计了一种前冲击发式可变后坐阻力变开孔自动迫击炮，该自动迫击炮可在不改变装药量的情况下(最大装药量)，仅通过改变开孔大小即可实现变初速发射，简化了操作，易于自动化改造。同时，由于采用了可变后坐阻力制退复进机，该自动迫击炮可以保证在不同开孔大小情况下的自动循环过程的稳定可靠。该自动迫击炮的优势在于可在保证火力覆盖范围的前提下，减轻后勤负担，提高勤务性以及火力灵活性，可为实现迫击炮的无人化和智能化提供基础。

1 变开孔迫击炮内弹道理论

1.1 基本假设

根据经典迫击炮的装药及其内弹道过程的特点，并结合开孔时的火药燃气泄露现象，提出以下假设[10-11]：

1)基本药管内的火药瞬时燃烧完，并在该时刻火药气体全部自传火管孔流出，均匀充满弹后空间，同时附加药包在点火药作用下全面点燃，迫击炮弹开始起动；

2)火药的燃烧服从指数燃烧定律；

3)火药的燃烧和迫击炮弹的运动在平均压力下进行；

4)内弹道过程中的热散失不作直接计算，而是通过减小火药力的方法，间接修正热损失对内弹道过程的影响；

5)气体从间隙及可变开孔中流出时，满足临界状态的条件。

1.2 工作原理

简化的变开孔迫击炮如图1所示。炮闩前冲带动迫击炮弹向前运动，指定位置击发，记击发位置为x=0；当迫击炮弹被击发后，其在火药燃气的推动下向前运动，前冲中的炮闩逐渐减速并向后运动；与此同时，火药燃气于可变开孔处泄出，火药燃气的流量由可变开孔大小控制。

1.3 内弹道方程

参考迫击炮经典内弹道方程[10-11]，推导变开孔迫击炮内弹道组。

1)喷口未打开前，基本装药定容燃烧的计算公式如下：

(1)

式中：Δ1=ω1/Vd，ω1为基本装药的装药量，Vd为尾管容积；ρp为火药密度；pTK为破孔压力；χ1、λ1为基本装药的形状特征量。

2)基本装药和辅助装药混合燃烧阶段基本方程如下：

(2)

式中：

(3)

(4)

(5)

3)初始条件：t=0，v=l=η=Z2=0，Z1=Z0。

(6)

式中ΔT=ω1/V0；Δi=ωi/V0，ωi为第i号辅助装药质量；V0为药室容积；CT为热损失修正系数。

综合式(1)～(6)，即可求得变开孔迫击炮的内弹道诸元。

1.4 初速分级

查阅文献[12]得到某型迫击炮的装药号、装药量及初速分级，并将其作为变开孔迫击炮的目标初速，分别求得在最大装药量情况下，变开孔迫击炮达到对应初速所需的开孔面积，计算结果如表1所示。

表1 某型迫击炮初速分级及所需开孔面积

由计算结果可知，当开孔面积为0.203 7 dm2时，其初速可达到传统迫击炮0号装药的初速。在理论上可以在0～0.203 7 dm2的范围内调节开孔面积，从而使迫击炮无极变初速，在不改变装药量的情况下实现射击死区的最小化。

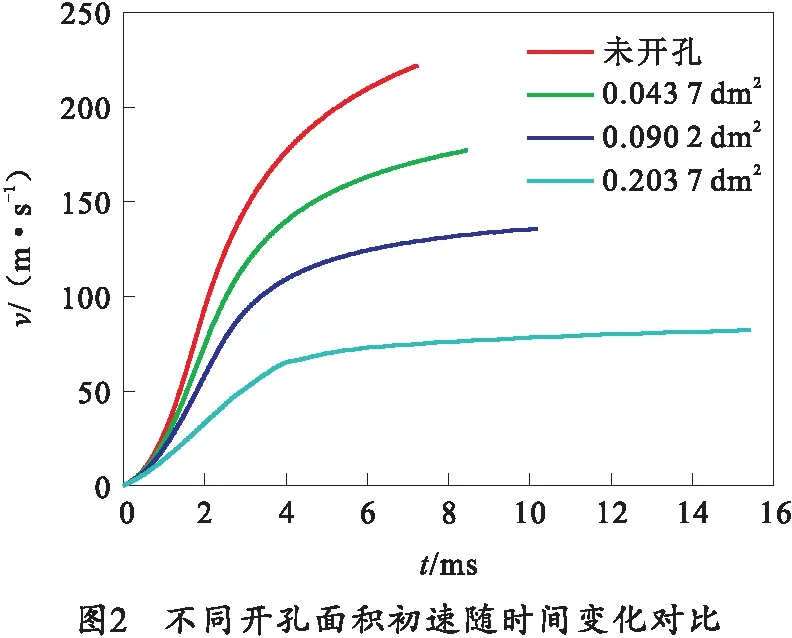
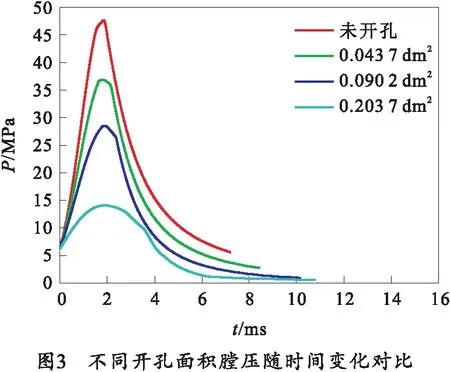
变开孔迫击炮在4种不同开孔大小下，迫击炮弹速度及膛内压力随时间变化的曲线如图2、3所示。由图可知，由于可变开孔的泄压作用，随着开孔面积的增大，变开孔迫击炮的膛内压力下降，使火药燃速降低、弹丸速度降低。并且其内弹道时间会有所延长，在开孔面积为0.203 7 dm2时内弹道时间达到了15.43 ms，相比于不开孔时的内弹道时间7.23 ms延长了117.47%。

2 可变后坐阻力制退复进机

2.1 结构原理

笔者设计的前冲击发式可变后坐阻力变开孔自动迫击炮如图4所示，其工作原理与“矢车菊”82 mm自动迫击炮[6]相同。不同点在于：其一，该自动迫击炮于迫击炮弹击发处加装了一套变开孔机构，用于改变开孔大小；其二，对制退复进机进行了改进设计，使其具有可变后坐阻力能力以匹配变开孔迫击炮内弹道特性。

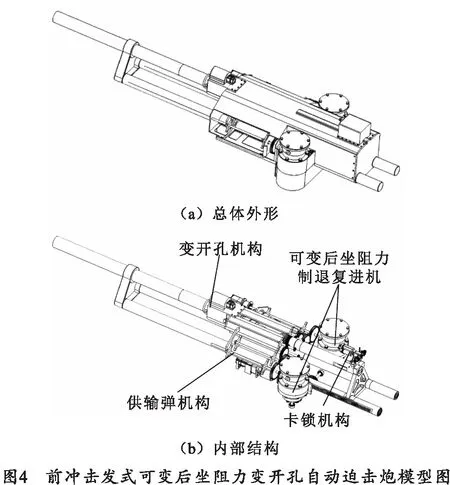
由变开孔所造成的自动循环过程不一致问题，则可由可变后坐阻力制退复进机解决。

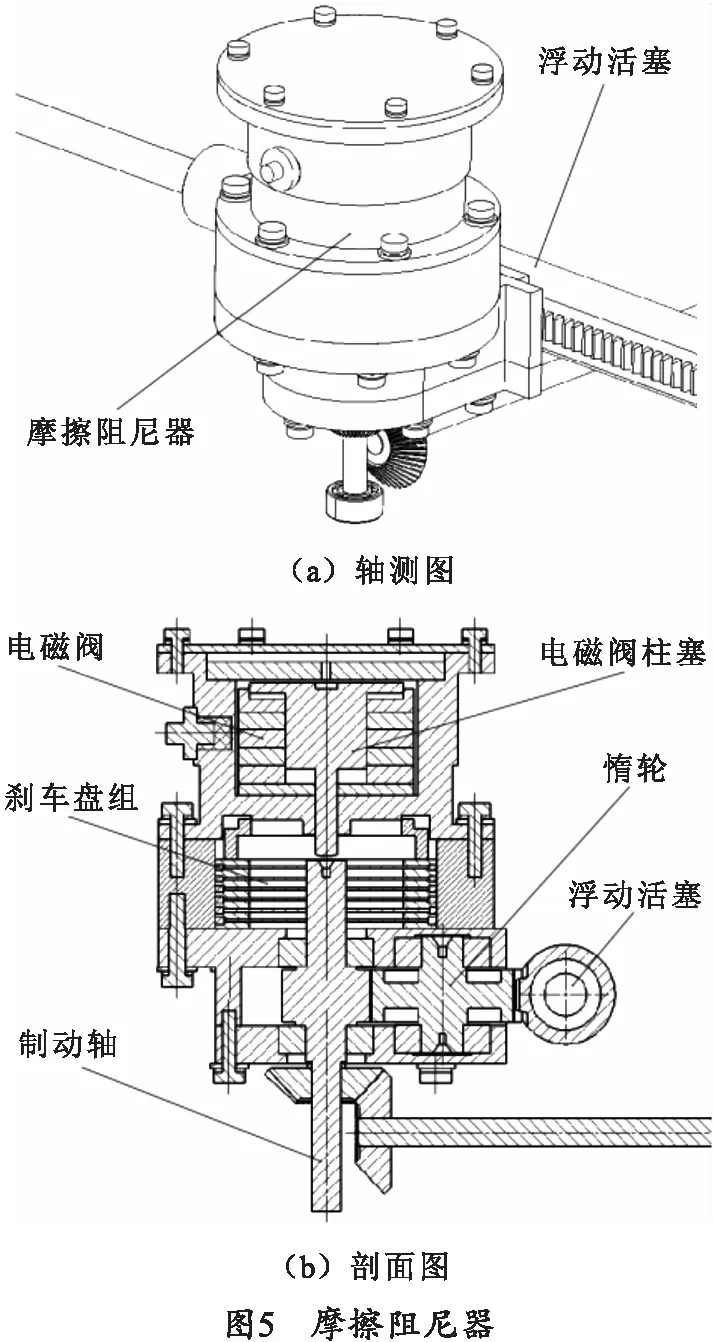
可变后坐阻力制退复进机的可变后坐阻力功能由呈对称布置的两个摩擦阻尼器实现，如图5所示，主要由电磁阀、电磁阀柱塞、刹车盘组、惰轮和制动轴组成。其电源及控制信号可由接口传入，同时，可使用角速度传感器检测制动轴转速，实现对摩擦阻尼器的制动效果监测。由接口输入的电源及控制信号可以调节电磁阀电流的大小，实现控制电磁阀柱塞向下的推力，进而控制电磁阀柱塞对刹车片组的压力。刹车盘组所受压力越大，摩擦力也就越大，则对刹车轴的制动效果越强，而刹车轴通过与惰轮啮合可以将制动力传递给同样与惰轮啮合的浮动活塞，以实现制动动作。且由于自动迫击炮的后坐行程较长，摩擦阻尼器有充足的作用时间，所需的摩擦阻力也较为合理。

2.2 自动循环过程

在前冲阶段，炮闩在与之相连的浮动活塞内复进簧的推动下向前运动，当前冲至击发位置时，迫击炮弹被击发，炮膛合力开始作用于炮闩，使其减速并后坐；在后坐阶段，摩擦阻尼器和复进簧同时对炮闩进行制动，当后坐到位时，两者产生的合力可将炮闩的动能完全消耗，此时摩擦阻尼器停止制动动作。不需要额外的缓冲簧来提供缓冲，则炮闩就不会出现使用传统缓冲器时的振荡现象，同时也在最大程度上减小了对炮尾的冲击。如若当炮闩后坐到位时处于单发状态，则卡锁机构卡住炮闩，使炮闩停止运动，单个自动循环结束；如若处于连发状态，则炮闩继续在复进簧的推动下向前运动，继续下一个自动循环。

炮闩进行复进运动和后坐运动时的微分方程分别为

(7)

(8)

式中：mh为炮闩及后坐部分质量；md为迫击炮弹质量；Ff为复进簧提供的复进力；Fpt为炮膛合力；Fmc为后坐部分与导轨之间的摩擦力；Fkb为摩擦阻尼器提供的可变后坐阻力。式(7)、(8)为炮闩动力学方程的基本表达式。

3 内弹道匹配性研究

3.1 不同开孔情况下的炮膛合力计算分析

当开孔面积变化时，变开孔迫击炮内弹道时期的膛压及其他内弹道诸元皆会随之改变。采用参考文献[13]中的炮膛合力计算方法对不同开孔大小情况下的炮膛合力进行计算，可得对应的炮膛合力如图6所示。

在分析了变开孔迫击炮的炮膛合力后，可以得出不同开孔大小下的炮膛合力冲量，如表2所示。

表2 不同开孔大小炮膛合力冲量

由表2可知，当开孔面积为0.203 7 dm2时，其炮膛合力冲量仅为未开孔时的33.57%，两组开孔面积对应的炮膛合力冲量相差较大，会造成复进簧弹簧刚度与摩擦阻尼器摩擦阻力之间的失衡，不利于制退复进机的参数设计，故应当舍去最大开孔面积，仅使用前3组开孔面积进行进一步分析。

3.2 变后坐阻力制退复进机数值分析

根据上述推论，进一步对3种不同开孔大小的变后坐阻力制退复进机进行数值仿真分析。通过动力学数值计算，以验证该制退复进机的可行性。

将前文求得的不同开孔大小情况下的炮膛合力代入动力学方程(7)、(8)，并进行数值计算，可得不同开孔大小所需的摩擦阻力，如表3所示，不同开孔大小单发时的炮闩速度随位移变化曲线如图7所示，不同开孔大小5连发时的炮闩位移及速度随时间变化曲线如图8、9所示。

表3 不同开孔大小所需摩擦阻力

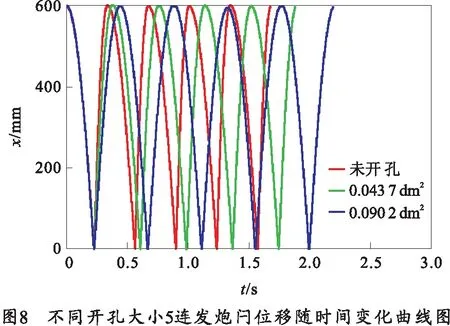
图7中纵坐标为炮闩运动速度，正值表示后坐，负值表示复进；横坐标为炮闩位移，击发点为5.0 mm处，由图7可知，炮闩在迫击炮弹被击发后的最大前冲量为6.1 mm，当迫击炮弹被击发后且到达最大前冲位置时，摩擦阻尼器立即开始工作，于后坐全行程中持续制动，与复进簧一同吸收炮膛合力所产生的后坐能量。当开孔大小变化时，调节摩擦阻尼器所施加的摩擦阻力以匹配不同开孔大小情况下的炮膛合力，使后坐到位的位置一致，从而保证前冲速度的一致性，使自动循环过程得以可靠进行。

由图8、9可以看出，由于采用了与变开孔迫击炮相匹配的可变后坐阻力制退复进机，自动机保证在连发状态下的自动循环过程平稳可靠；并且可以更为精确地控制后坐到位时的速度，使后坐到位冲击较小，不需要额外的后缓冲簧进行缓冲，使其自动循环时间更短，所以其理论射速最高可达178 发/min，相对于传统自动迫击炮的理论射速150 发/min[5]提高了18.67%。