纱线间距对复合材料拉伸性能的影响

谢 旺， 成小乐*， 孙 戬， 李 阳， 赵瀚辰

(1.西安工程大学 机电工程学院， 陕西 西安 710048； 2.西安热工研究院有限公司， 陕西 西安 710048)

芳纶橡胶基编织复合材料作为一种新型高性能材料日益受到关注，广泛应用于制造领域。橡胶基编织复合材料与传统材料相比具有很强的可设计性，通过对其各组成相的合理配比能够弥补原有组分的缺点，以此来改善橡胶基材料的耐磨性和抗刺穿能力。该方法是使橡胶基材料强度高且耐久的重要研究方向，其中二维编织则是橡胶基编织复合材料中最为广泛的一种[1-2]。

针对编织结构对复合材料拉伸性能的影响，国内外学者提出了不同的细观模型。付金毅等[3]考虑编织结构建立了石英复合材料的单胞模型，研究了编织角对复合材料拉伸性能的影响;当编织角大于50°时拉伸模量及强度随着编织角的增加而减少。马晓红等[4]将二维编织管平压为双层织物，并与环氧树脂复合，结果表明编织对纤维的损伤较小，最大损伤率为20.77%。编织角对拉伸性能的影响为主要因素，拉伸强度和拉伸模量随着编织角的减小而增大。屈鹏[5]考虑了纤维束的横截面几何尺寸对应力分布的影响，建立了不同编织角的单胞模型，并分析其力学性能，结果表明对于纤维体积分数相同的单胞模型编织角对复合材料的弹性模量影响很大。BYUN等[6]采用编织复合材料结构几何模型结合体积平均法对拉伸性能进行预测。TABIEI等[7]通过考虑纤维束的截面尺寸，建立了编织复合材料单胞模型，并设想建立的单胞模型符合等应力应变规律，通过增量理论构造材料的刚度矩阵，来研究其拉伸性能。在上述文献的研究中，所采用的细观模型大多为考虑纤维束的编织角以及自身的几何尺寸对拉伸性能的影响，个别学者考虑了纤维体积，但尚未全面考虑纱线间距对纤维体积和拉伸性能的影响。

课题组以芳纶增强橡胶基编织复合材料为研究对象，根据制备出的复合材料几何尺寸和结构为原型，构建出不同拉伸方向下4组纱线间距的复合材料单胞模型；并利用有限元软件对单胞模型的拉伸性能进行仿真，得出纱线间距对复合材料拉伸性能的影响规律；并通过0.79 mm芳纶增强橡胶基编织复合材料的拉伸实验来验证。

1 有限元模型建立

1.1 单胞选取

对复合材料宏观力学性能和几何结构单胞模型的力学性能预测相结合是二维编织复合材料力学性能的研究方向[8]。芳纶纤维增强橡胶基复合材料具备细观结构的周期性，可以采用复合材料代表性体积单元-单胞模型进行有限元分析[9-10]。图1为芳纶橡胶基编织复合材料的实体试样和单胞模型，图1(a)为制备的复合材料纤维结构图，内部纤维束在经、纬2个方向之间平纹相织，因此复合材料的力学性能在经向和纬向得到加强。根据芳纶纤维橡胶基复合材料的细观结构，利用建模软件建立实体模型，并取细观结构上的最小周期性重复单元作为单胞模型，如图1(b)所示。其中，所构建的单胞模型基体和增强体的体积分数与宏观状态下制备的编织复合材料一致。

图1 单胞模型的选取Figure 1 Selection of unite-cell model

1.2 单胞结构参数

根据二维编织复合材料细观结构的特点[11-13]，对芳纶纤维橡胶基复合材料单胞模型提出以下假设：①纤维束截面形状为圆形且直径为d；②经纱与纬纱的纱线间距相等且长度为L。芳纶增强橡胶基编织复合材料的细观结构如图2所示。为了研究纱线间距对芳纶纤维橡胶基复合材料细观力学性能的影响，建立了不同纱线间距的单胞模型，其纱线间距分别为0.79，0.85，0.95和1.05 mm。纤维束直径为0.3 mm，单胞模型总厚度0.8 mm，纤维增强层厚度0.7 mm。

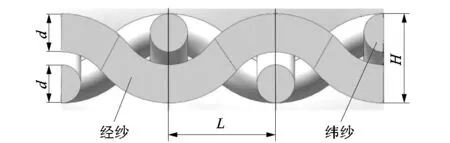
图2 复合材料细观结构Figure 2 Macro-structure of composites

1.3 材料参数

纤维材料为芳纶Ⅱ(PPTA)，基体相为二元乙丙橡胶(EPM)，平纹织物与橡胶材料各向同性，复合材料性能参数如表1所示[16]。

表1 复合材料各组分性能

1.4 周期性边界条件

编织复合材料可以假设为由多个单胞模型周期性组合而成，为了将单胞模型的力学性能等效为复合材料的宏观力学性能，则需要对单胞模型施加周期性边界条件，使每一个单胞模型之间保持连续的位移和应力，得到更为精准的应力和应变。

在有限元软件中设置拉伸边界条件，将单胞模型一端固定，另一端沿拉伸方向施加5 MPa的拉伸载荷，模拟复合材料的单轴拉伸实验过程。考虑到拉伸方向对编织复合材料拉伸性能的影响，从而选择纤维束交织方向和经(纬)纱方向2种单胞模型进行拉伸，拉伸方向如图3所示。考虑单胞模型的复杂性，纤维束和基体均采用四面体网格进行划分，共计网格25 207个。纤维束与纤维束之间、纤维束与基体之间不考虑摩擦均采用绑定的方式进行连接。以经(纬)纱与拉伸方向成45°夹角为纤维束交织方向，经(纬)纱与拉伸方向平行为经(纬)纱方向。

图3 边界载荷的施加Figure 3 Application of boundary loads

2 结果与分析

2.1 复合材料拉伸实验

委托合作单位制备出纱线间距为0.79 mm的芳纶橡胶基编织复合材料，并将实验试样沿经纱方向裁剪出矩形布条，得到图4(a)中的试样；将试样固定在图4(b)所示的拉力试验机中，试样在拉伸过程中被拉力试验机的上下夹具固定，并对试样施加恒定载荷进行单轴拉伸。通过电脑采集得到试验所需的拉伸时间和应力应变等数据。

图4 复合材料拉伸实验Figure 4 Composite tensile experiment

2.2 单胞模型有限元模拟

2.2.1 纤维束交织方向

还有一部分一线复合肥企业老总凭借敏锐的洞察力，已经意识到：“传统玩法已经搞不定，传统渠道需要借势、转型快，才能获得‘生存权’。” 一些传统肥料企业已经抢先一步拥抱终端、尝试改变。“我们也开始逐步学习直供模式，将农药、肥料的圈子汇聚在一起。”

纤维束交织方向下基体表面的等效应力如图5所示。从图中可以看出，基体的应力分布具有对称性，不同纱线间距的基体在经纱和纬纱交织的部位等效应力高于其它部位，存在较为严重的应力集中。随着纱线间距的不断增加，基体的最大等效应力呈逐渐增大的趋势。0.79，0.85，0.95和1.05 mm纱线间距基体最大等效应力分别为1.496，1.796，2.311和2.751 MPa，表明纱线间距的增大会导致基体材料承受的应力增加。

图5 交织方向基体应力云图Figure 5 Stress nephogram of matrix with fiber interweaving direction

纤维束交织方向下纤维束表面的等效应力如图6所示。纤维束应力最大区域出现的位置与基体中应力最大区域空间基本一致。复合材料的基体和增强相2者之间的等效应力相差较大，纤维束承受较大部分的拉伸载荷；且纤维束经纱与纬纱交织处应力集中显著，原因为经纬纱之间会接触摩擦而产生力的传递，此部位是增强相容易被破坏的点。0.79，0.85，0.95和1.05 mm纱线间距下增强相的最大应力分别为538，551，602和624 MPa，表明随着纱线间距的增大，纤维束交织部位上的应力呈逐渐增大的趋势。原因是随着纱线间距的增加，纤维束在复合材料中的体积分数在逐渐减少，致使其承受的载荷进一步增大。

图6 交织方向增强相应力云图Figure 6 Stress nephogram of fiber reinforcement with fiber interweaving direction

2.2.2 经(纬)纱方向

经(纬)纱方向下基体表面的等效应力分布如图7所示。基体的最大应力出现在经(纬)纱与基体相接触的部分。对比纤维束交织方向，基体在受到同样拉伸载荷的作用下应力小于交织方向，基体的等效应力同样随着纱线间距的增加而增大。0.79，0.85，0.95和1.05 mm纱线间距下基体最大等效应力分别为0.242，0.256，0.269和0.286 MPa，相较于纤维束交织方向的等效应力有所减少。

图7 经(纬)纱方向基体应力云图Figure 7 Stress nephogram of matrix with warp (weft) yarn direction

经(纬)纱方向下增强相表面的等效应力如图8所示。增强相上的最大应力点和交织方向一样出现在了经纬纱交织部位。0.79，0.85，0.95和1.05 mm纱线间距处织物的最大应力分别为256，273，299和321 MPa，相较于交织方向经由纤维束接触和摩擦导致破坏的现象有所减缓，等效应力减少。

图8 经(纬)纱方向增强相应力云图Figure 8 Stress nephogram of fiber reinforcement with warp (weft) yarn direction

2.3 有限元模拟准确性分析

为了验证单胞模型预测的准确性，在图9中将纱线间距为0.79 mm的复合材料拉伸试验得到的应力、应变与有限元模拟的数据进行对比。可以看出2者数据趋势基本相同，以此来验证通过计算机模拟得到数据的合理性。由于纤维束在复合材料中的轨迹分为直线段和曲线段，致使纤维束在拉伸过程中应变产生的方式有所不同。应变较低时，纤维束随着应变的增加在曲线段随着拉伸逐渐变直，应变较高时，纤维束的应变则来自纱线的伸长。

图9 纱线间距0.79 mm时应力-应变曲线Figure 9 Stress-strain curve at 0.79 mm yarn spacing

2.4 复合材料力学性能预测

2.4.1 材料性能

图10为不同纱线间距下的应力-应变曲线。从图10可以看出芳纶橡胶基编织复合材料不同纱线间距的经向拉伸应力-应变曲线几乎呈线性关系。原因在于拉伸方向与纤维束的编织方向一致，纤维束作为拉伸载荷的主要承载体，其力学性能自然表现为纤维的线性关系。橡胶基体与纤维增强体2者之间刚度和弹性模量相差较大，因此基体产生微小的非线性刚度关系可以忽略。随着纱线间距的增加，等效应力的最大值有着降低的趋势；而纤维束体积分数的降低，也导致复合材料的刚度随之下降。

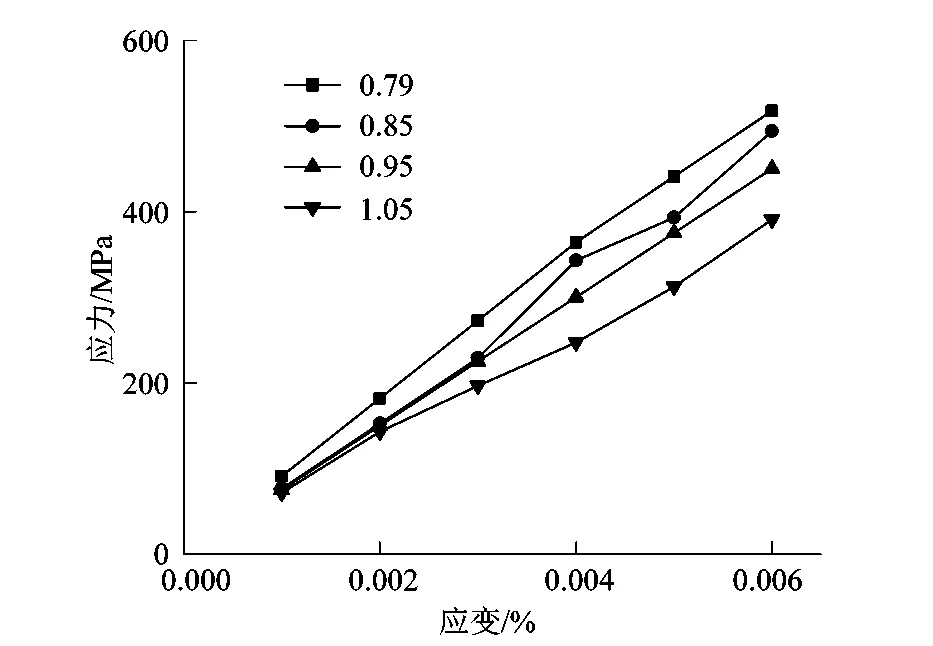
图10 不同纱线间距下的应力-应变曲线Figure 10 Stress-strain curves at different yarn spacings

2.4.2 等效弹性模量计算

芳纶纤维增强橡胶基复合材料由橡胶基体和芳纶织物增强体组成。由于复合材料在细观结构上成分不均一，在承受外部载荷时，基体和增强体所承受的应力和应变也不完全一样，因此在研究复合材料细观力学时，需要引入均质化理论，将复合材料的细观力学性能转化为宏观力学性能[18]。

单胞模型的平均应力为：

(1)

单胞模型的平均应变为：

(2)

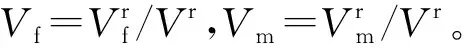
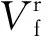
根据式(1)和(2)的等效弹性模量计算方法，得到不同纱线间距下的等效弹性模量如11所示。

图11 复合材料等效弹性模量Figure 11 Equivalent elastic modulus of composites

从图11可以看出在同等纱线间距下经(纬)纱方向的等效弹性模量高于纤维束交织方向，且平均高出21%。由于复合材料中纤维束所占的体积分数决定了复合材料的承载能力，而纱线间距的增加致使纤维束体积分数随之下降，导致其拉伸性能降低。因此单胞模型的等效弹性模量随纱线间距的增加而降低。

3 结语

为探究纱线间距对编织复合材料拉伸性能的影响，课题组通过建立不同拉伸方向下4组纱线间距的芳纶纤维橡胶基复合材料单胞模型，利用有限元软件对单胞模型进行拉伸仿真分析，并通过制备的0.79 mm芳纶橡胶基编织复合材料的拉伸试验对有限元模拟的准确性进行了验证，得到了以下结论：

1) 随着纱线间距的增加，芳纶纤维橡胶基复合材料单胞模型中的基体和增强体的应力均会增加，且经纬(纱)方向上的等效应力小于纤维束交织方向。

2) 复合材料不同纱线间距的经向拉伸应力-应变曲线几乎呈线性关系，并且随着纱线间距的增加，等效应力的最大值有着降低的趋势。

3) 通过均质化理论计算的复合材料等效弹性模量表明随着纱线间距的增大等效弹性模量逐渐减少，且经(纬)纱方向的等效弹性模量平均高于织物交织方向21%。

课题组模拟了4组纱线间距下不同拉伸方向的芳纶纤维橡胶复合材料的拉伸性能，还不能精确得出纱线间距对复合材料拉伸性能影响的能力，之后还需要对大量的纱线间距进行分析计算。