考虑多车型的柔性制造车间双向物料配送路径优化
2023-03-01张守京刘跃强
徐 进, 张守京, 刘跃强
(西安工程大学 机电工程学院, 陕西 西安 710600)
随着柔性制造企业的不断发展,其生产模式正朝着个性化、多品种和小批量演变[1-2]。生产模式组织难度加大,因此生产加工所需的物料应当及时有效正确地送达各个工位,除了正向物流,往往还面临着退单、产成品回收等逆向物流的问题。物料配送环节作为车间制造过程的重要组成部分,它的效率高低直接影响着制造过程的生产效率,因此,车间物料配送的研究就显得格外重要。
车间物料配送路径优化问题是车辆路径问题(vehicle routing problem,VRP)的一个分支,自1959年Dantzig等[3]提出了VRP至今,国内外学者对其进行了大量的研究。Bouchra等[4]提出了遗传算法和变邻域搜索算法相结合的混合求解方法;Chen等[5]使用改进的蚁群算法和禁忌搜索算法进行求解;涂海宁等[6]提出了一种改进的蚁群算法求解装配车间送料路径寻优模型;在车间物料配送方面,吴倩云等[7]构建了考虑时间窗和装载约束的最优配置模型;党少杰等[8]以配送路径最短为目标,建立了单任务和多任务的物料配送模型;马磊磊等[9]构建了基于模糊时间窗的多目标模型,并提出了改进遗传算法进行求解;在双向物流车辆路径问题方面,周蓉等[10]提出了一种自适应并行遗传算法;张守京等[11]提出了一种车间物料配送与余废料回收协同的路径优化方法;孙宝凤等[12]建立了基于实时信息的取送货动态车辆路径模型;NEPOMUCENO等[13]设计了快速随机算法来求解车辆异构的同时取送货的车辆路径问题(vehicle routing problem with simultaneous pick-up and delivery,VRPSPD);Gong等[14]设计了一种2阶段多目标混合算法;马艳芳等[15]考虑了环境的不确定性,提出一种基于模糊随机算子的改进粒子群算法;在多车型车辆配送方面,Jamil等[16]运用萤火虫算法研究多车型车辆情况下的路径优化问题;Wang等[17]提出一种改进自适应遗传算法,求解城市交通约束下的多种车型车辆路径优化问题;鲍伟等[18]考虑了软时间窗并引入自适应竞争策略证明了使用多车型能有效降低物流成本;刘思远等[19]结合多车型碳排放计算方法提出了一种改进的双策略种群协同蚁群算法验证了模型的有效性;狄卫民等[20]提出了一种考虑动态拥堵的多车型绿色车辆路径优化方法。
笔者在柔性制造车间物料配送研究现状的基础上,分析以上文献发现柔性制造车间目前存在如下问题:对于车间内物料配送的VRP较少有研究考虑车间余废料的回收,且研究重点多为求解算法的创新与融合;同时,在实际车间物料配送中,往往不只是1种型号的小车参与配送任务,通常有2种及以上不同的小车共同进行配送,但考虑多车型相关的研究大多数为车间外部冷链物流。为了提高小车利用率,有效地降低配送成本,因此在车间物料配送路径优化问题中考虑多种车型及回收显得很有必要。综上,笔者提出了一种考虑多车型的车间双向物料配送路径优化策略,并以配送各成本总和为优化目标建立相应的数学模型;同时为了提高遗传算法进化后期的搜索效率,针对交叉变异概率进行改进;最后通过仿真实验对模型和算法的可行性及有效性进行验证。
1 模型的建立
1.1 问题描述
本研究主要是在满足各个工位对物料数量不同需求的前提下,将订单分配给不同型号的各个配送小车,最后小车将分配到的订单依次对应各个工位服务。在满足车的载质量、数量等约束下,计算出每个方案的总成本,最后选择出总成本最低的那个配送方案。每个方案因选择的车型及小车数量的配置大不相同,所需的配送总成本也就各不一样。为了最大程度地节约成本,因此如何合理安排不同车型及小车数量进行配送显得非常重要。
如图1所示,在确定好方案之后,不同型号的小车从物料仓库将工位所需的物料分别送至各个工位点,到达工位点后采取先卸载后装载的顺序直至配送任务完成,最后将回收的废料等运到回收仓库。
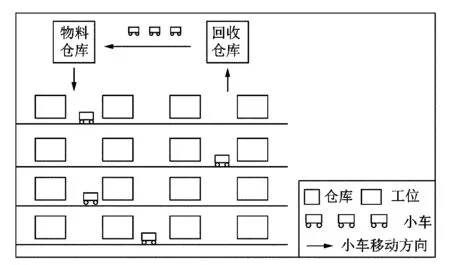
图1 多车型配送示意图Figure 1 Multi-vehicle distribution map
基于上述问题分析,假设以下条件成立:
1) 物料中心及各个工位的位置都已知且配送过程中的各个节点都能通过;
2) 物料中心和各型号的小车数量已知;
3) 每个工位的需求量及回收量已知,时间窗和最佳配送时间也已知;且各型号小车的最大载质量及速度已知且恒定;
4) 每辆车只能对1个工位进行配送,及每个工位的任务不能拆分成由2辆及以上车辆进行配送;
5) 进行配送任务的车只能从物料中心出发,完成配送任务后返回物料中心;
6) 参与配送的小车任何时间载质量不能超过该型号小车的最大载质量;
7) 配送时间满足各工位时间窗,超出时间窗则设置惩罚;
8) 假设装卸无时间及成本消耗。
1.2 数学模型的构建
根据以上描述,针对需要解决的问题,以总成本最低为目标函数构建多车型车间双向物料配送的模型。

(1)
∀i,j∈N,k∈K,m∈Mk。
(2)
∀i∈N,k∈K,m∈Mk。
(3)
(4)
qi-hi≥0,∀i∈N。
(5)
(6)
(7)
(8)
(9)
(10)
(11)
式(1)为包括发车的固定成本、运输成本和时间惩罚成本的总成本最小的目标函数;式(2)和式(3)为只能取0或1的决策变量;式(4)为进行配送车辆运输货物的容量不超过该型号车辆的最大容量;式(5)为任意工位的回收量不能超过需求量;式(6)为参与配送的小车数量要在该车型总数之下;式(7)为保证每个工位只能被某车型的某车辆服务1次;式(8)为小车的起点和终点都是物料中心;式(9)为小车配送至某工位后,必须从该工位离开才能再进行下一步移动;式(10)为小车要在工位要求的时间窗内送达;式(11)为时间惩罚成本函数,当小车到达工位的时间在时间窗外则产生时间惩罚成本。
2 改进遗传算法求解模型
2.1 编码与解码
在求解的问题中往往不止1辆车1种车型进行配送,为了直观地展示各小车的配送的任务,采用自然数编码。km为k种型号的第m辆车,101,201和301表示3种不同型号的第1辆小车;1,2,3,…,N表示各个工位。
由4辆3种不同型号的小车执行配送任务的染色体编码示意图如图2所示。车型3的第1辆小车配送工位为6—7;车型1的第1辆小车配送工位为4—2—2*—8;车型1的第2辆小车配送工位为3—1;车型2的第1辆小车配送工位为5。

图2 编码示意图Figure 2 Coding schematic
2.2 种群初始化
在算法正式开始求解之前,先对种群进行初始化操作;将各个工位分配给不同型号的不同小车,并按照优先级顺序依次进行配送,直至完成任务。
初始化步骤如下:
1) 随机生成100条1~N个工位的染色体,将所有工位随机分布在每条染色体上;
2) 从第1个工位开始给其分配小车,重复该操作至最后1个工位,并按照配送的优先级给各车辆配送的工位进行重新排序,完成1条染色体的任务分配;
3) 重复上述步骤直至种群规模达到预定的数量。
2.3 适应度函数
笔者以总成本最小为目标函数,将总成本的倒数作为适应度函数,适应度函数如式(12)所示。
(12)
2.4 选择操作
按照适应度的大小将上一代种群从大到小进行排序,从中选择适应度前80%的个体,将把它们保留至下一代种群。
2.5 改进交叉操作
动态自适应适用于进化后期,不适于进化前期,因为前期的优秀个体有可能是局部最优点,所以在进化前期设定Pc=0.9,Pm=0.1,恒定;在进化后期,采用动态自适应交叉变异概率。根据选择操作保留下的个体适应度的不同来选择不同的交叉变异概率。交叉概率选择公式为:
(13)
式中:fmax和favg分别为上一代种群适应度的最大值与平均值,f为进行交叉操作的2个个体适应度的平均值。
当种群中个体适应度值小于种群平均适应度值时,选择增大交叉概率,加快新个体产生的速度;当个体适应度值大于种群平均适应度值时,减小交叉概率,保留优秀个体。选择好交叉概率之后,进行交叉操作,具体操作如图3所示,随机产生2个交叉点1和5,将交叉点及其右侧相邻的片段依次置于另一个染色体的前端,最后剔除相同的基因,完成交叉。
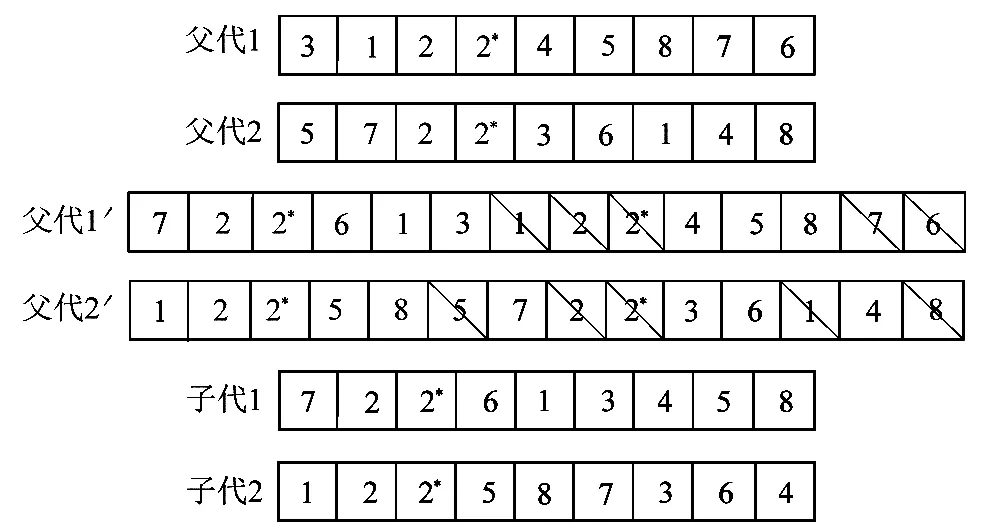
图3 交叉操作示意图Figure 3 Schematic diagram of crossover operation
2.6 改进变异操作
同理,采用动态自适应变异概率,变异概率选择公式为:
(14)
式中fm为进行变异操作个体的适应度。
如果变异概率Pm过小,不易产生新个体结构;Pm过大,变成纯粹的随机搜索。当没达到最优解,求解停滞不前的时候,可以适当调整变异概率。当随机数的值小于变异概率,则进行变异操作。具体变异操作采用多点交换变异,如图4所示,在进行变异操作的染色前半段随机选择2个基因5和1,然后和其对应的后半段3和7进行交换生成新个体。

图4 变异操作示意图Figure 4 Schematic diagram of variation operation
2.7 求解步骤
改进遗传算法流程如图5所示,具体步骤如下:
1) 设置参数,初始化种群,计算种群的适应度;
2) 按照初始种群适应度的从大到小进行排序,选择适应度好的个体保留下来;
3) 进行交叉变异处理,生成新的个体重复上述步骤直至迭代次数为20;
4) 在进化后期执行自适应交叉变异操作,根据上一代种群进行交叉变异个体的适应度大小选择不同的交叉变异概率,产生新的个体,重复上述步骤直至迭代结束;
5) 保留最好个体。

图5 改进遗传算法求解流程图Figure 5 Improved genetic algorithm solution flow chart
3 实例仿真实验与分析
选择某电动车生产车间中A1至A5生产装配线作为研究对象,共32个工位的信息。用0工位表示物料仓库,0*表示回收仓库。以各个工位的最佳配送时间t*作为配送顺序的依据,依次给每个工位进行服务。算法参数设置如下:种群规模为100,Pc=0.9,Pm=0.1,最大迭代次数为500,借助MATLAB 2016a进行实例仿真验证。车辆相关参数如表1所示。

表1 车辆参数
物料仓库、回收仓库及各个工位信息如表2所示。
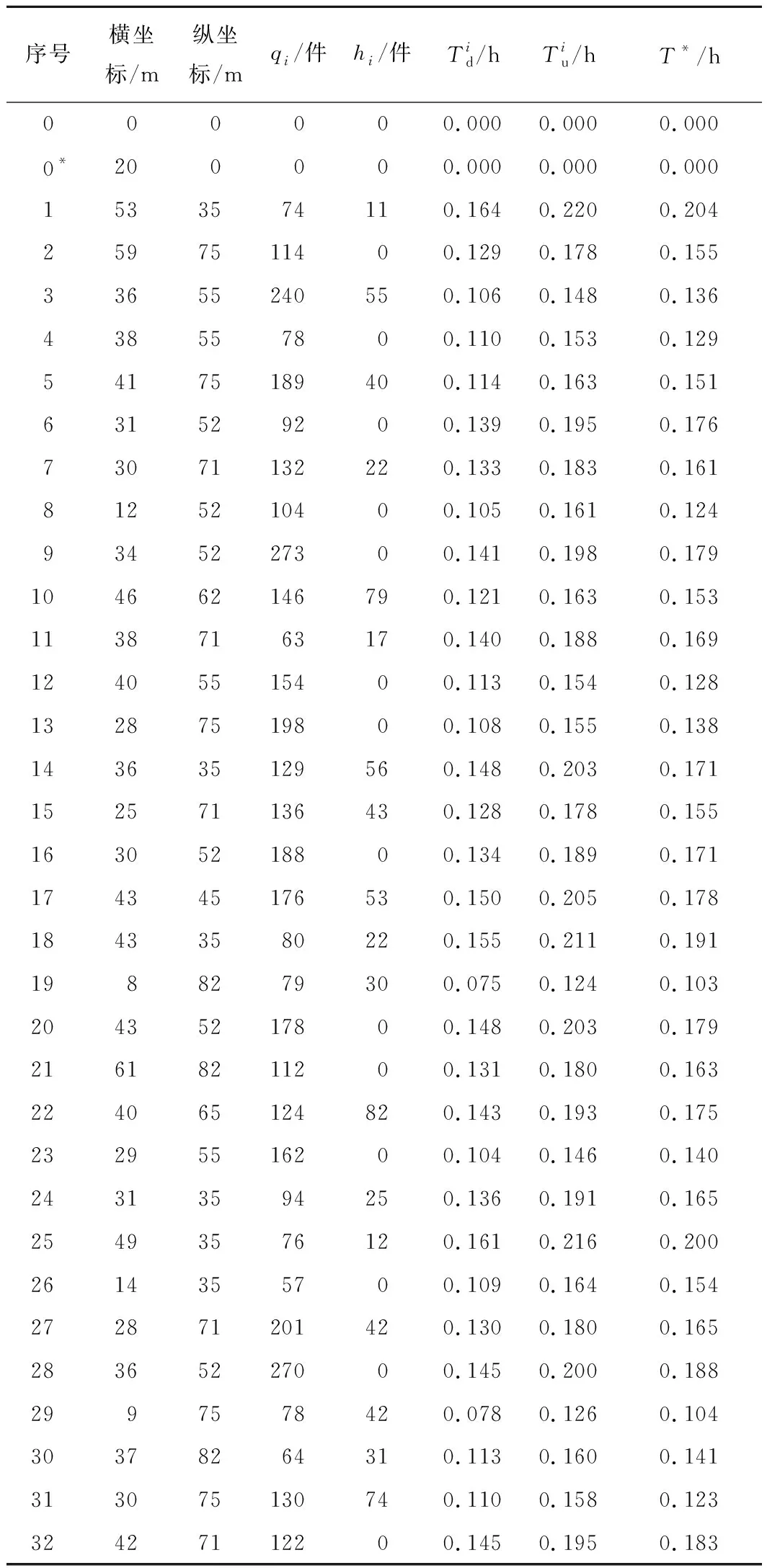
表2 仓库及工位信息
3.1 结果对比及分析
如表3所示,在满足相同的订单要求下,考虑双向配送策略的车辆装载率要比单独配送与单独回收之和要高3.68%;在配送总成本方面,更是能减少1 242.8元之多,证明了考虑双向物料配送策略的可行性及有效性。

表3 单配送单回收与双向配送对比
表4~6分别为采用遗传算法的单车型1、单车型2和单车型3的求解结果。只使用车型1,需要9辆才能完成订单需求,总成本为3 205.13 元;只使用车型2,需要7辆完成订单需求,总成本为3 142.46 元;只使用车型3,虽然只需要5辆就能完成订单需求,但总成本为3 237.42 元。表7为遗传算法求解多车型配送的结果,使用多种车型的小车共同进行配送求解结果总成本只需要2 985.08 元,相比只考虑单一车型所需总成本都要少。如图6所示,在使用遗传算法对实例求解的进化曲线中,可以明显看出考虑多车型的优越性,证明了多车型在车间双向物料配送中的有效性和可行性。

表4 单采用车型1遗传算法求解结果

表5 单采用车型2遗传算法求解结果

表6 单采用车型3遗传算法求解结果

表7 多车型遗传算法求解结果
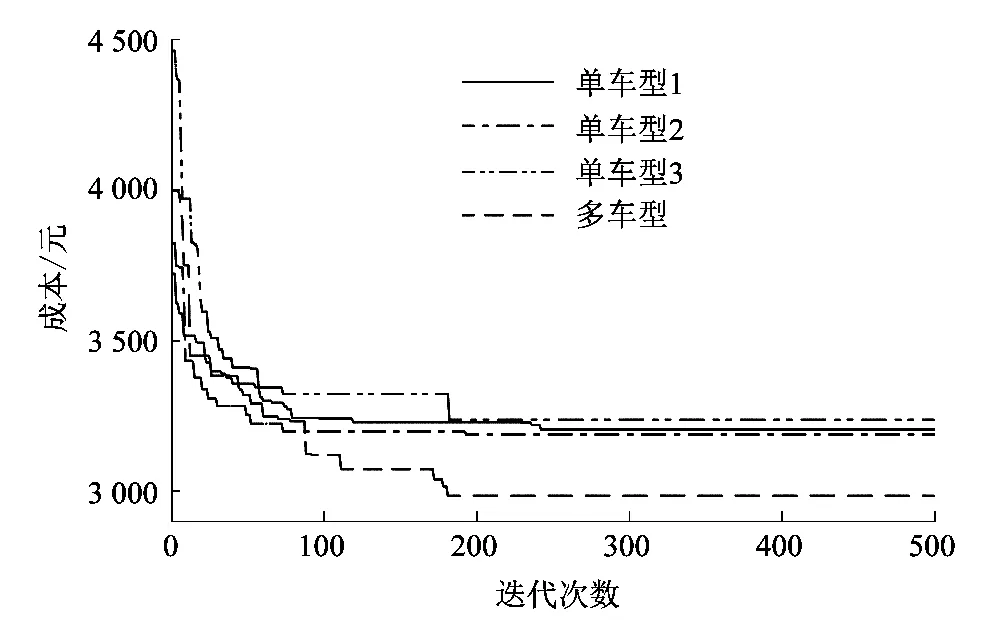
图6 遗传算法求解进化趋势Figure 6 Genetic algorithm for solving evolutionary trends
3.2 遗传算法改进前后对比分析
在上文的基础上,进一步对遗传算法进行了相应的改进,表8为多车型在改进遗传算法下求解的结果,共需6辆小车进行配送,总成本只需2 881.69 元。改进算法前后的进化曲线对比如图7所示。采用改进遗传算法求解方案总成本要较改进前低3.48%,证明了改进遗传算法的可行性及有效性。
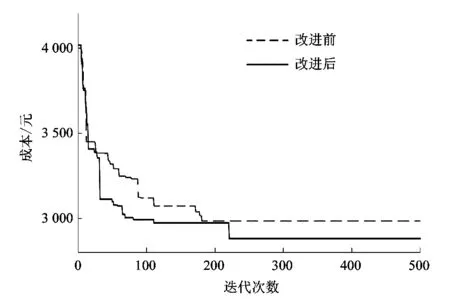
图7 改进遗传算法前后求解进化趋势Figure 7 Solving evolutionary trends before and after improving genetic algorithm

表8 多车型改进遗传算法求解结果
4 结论
笔者针对柔性制造车间出现的物料响应不及时、车辆装载率低等问题,提出了考虑多车型的车间双向物料配送策略,并以总成本最小为优化目标构建了对应的数学模型,分别利用遗传算法与改进遗传算法进行求解。最后,借助MATLAB对某电动车生产车间进行实例仿真,结果表明:多车型相比传统的单一车型更加适合现如今的柔性制造企业,能够有效地降低配送成本,还能提高小车的利用率;改进后的遗传算法与改进前算法求解结果进行对比,成本降低了103.4 元;相较于单车型3,成本更是降低了355.7元。验证了改进算法的可行性,表明了自适应遗传算法在解决离散制造车间问题的有效性。
在本研究基础上,今后将针对多车在配送过程中的动态交互及物料回收的不确定性进行研究,进一步贴近柔性制造车间的环境。
