基于小波变换的W18Cr4V图像去噪算法研究
2023-03-01何英杰石秀东张文利
何英杰, 石秀东, 陈 昊, 张文利
(江南大学 机械工程学院, 江苏 无锡 214122)
钨系高速工具钢在我国使用较多且应用较广,为精确计算退火状态下碳化物的含量和不均匀度[1],利用机器视觉技术对其进行定量分析,需要对采集的W18Cr4V退火图像进行预处理,其中最重要的步骤就是退火图像的去噪处理,因此课题组着重对退火图像的去噪算法进行研究。
随着机器视觉和图像处理技术的兴起,不少学者对图像去噪方法[2-5]进行了深入的研究。近年来由于小波变换[6]具有多分辨率,选择小波基函数灵活及去数据相关性等特点,使用小波变换进行去噪处理已经成为当下的一个热点问题。Dohono等[7-8]提出软、硬阈值函数去噪的方法,在实际图像去噪应用中取得了一定的成功,但同时也存在一些问题,比如硬阈值函数在阈值处断开导致不连续等,从而使得图像去噪过程中出现伪吉布斯效应,导致图像重构后出现振荡现象;又如软阈值函数虽在整个小波域处处连续,但由于重构后的信号与原信号存在固定偏差,去噪后会使得图像变得模糊,边缘和细节特征丢失。针对上述不足,不少学者提出了改进的算法。陈莉明[9]提出了一种高阶可导的阈值函数,通过改变调整因子不断地调节阈值和阈值函数,使得前、后信号的信噪比有所提高,达到了良好的去噪效果;檀雪等[10]提出一种具有良好连续性且参数可调的阈值函数,对心电信号进行去噪仿真,实验表明改进的函数可以增强去噪性能;李维松等[11]针对传统软、硬阈值函数去噪出现的图像失真和振荡现象等问题,构造出改进的小波阈值函数,并且阈值的选取更加灵活[12],MATLAB仿真结果表明改进后的函数可以提高信号的信噪比,去噪性能有所提升。上述方法虽一定程度上提升了小波去噪的效果,但是所提函数并不同时具有良好的连续性、高阶可导性以及逼近原始信号的性能,因此去噪效果提升不理想。
故课题组提出一种新的阈值函数的图像小波去噪算法,该阈值函数在阈值处连续且可导,避免在退火图像重构时出现图像失真等问题,重构后的图像与原始图像更接近,并且细节信息和边缘特征更清晰;同时提出了自适应调整阈值,当小波分解层数逐渐增加,阈值也随之减小,因此阈值具有良好的自适应性。
1 小波阈值去噪原理及步骤
1.1 小波去噪原理
图像小波去噪原理为:先将存在噪声的图像在多尺度上进行小波分解[13],将低分辨率下的小波系数全部保存;对于高分辨率情况下的小波变换系数,对噪声信号进行分析后所得的高频小波变换系数,设定一个恰当的阈值,将高频系数置为零,保持信号幅度大于阈值的小波变换系数,或对其进行“收缩”处理;最后用小波逆变换重构小波变换系数,使其恢复成达到去噪目的的有效图像。
1.2 小波阈值去噪的步骤
1.2.1 小波分解
选择恰当的小波基函数[14],对图像进行N层下小波分解,得到相对应的小波系数。目前常用于图像处理的小波基函数主要有db族、sym族、coif族等,在图像去噪中分解层数j一般取2~5。
1.2.2 阈值处理
选定阈值λ,将阈值λ和分解后的小波变换系数进行比较,将小波变换系数大于阈值λ的保留,小于阈值λ的置为零。常用的阈值选取方法有RiskShrink准则、SureShrink准则和VisuShrink准则等,其中VisuShrink准则较常用。VisuShrink准则采取固定阈值。
式中:σ是噪声的标准差,L表示图像尺寸或信号长度。
1.2.3 图像信号重建
将经阈值处理的高频小波变换系数及低频小波系数进行小波逆变换,重构图像获得降噪后的图像。
2 改进阈值函数及阈值的选择
阈值函数和阈值的选择直接影响图像的去噪性能。若阈值函数构造不佳,会导致图像失真或者重构后细节特征模糊;若阈值选取不适,也会适得其反。因此选取合适的阈值函数和阈值至关重要。
2.1 传统的阈值函数去噪算法
在传统的小波降噪方法中,一般采用软阈值和硬阈值函数来处理小波变换系数。
硬阈值函数:
(1)
软阈值函数:
(2)
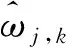
硬、软阈值函数图像如图1所示。


图 1 硬软阈值函数图像Figure 1 Hard and soft threshold function image
2.2 改进的阈值函数去噪算法
2.2.1 改进的阈值函数
结合传统硬、软阈值方法的优缺点,提出一种新的阈值函数:
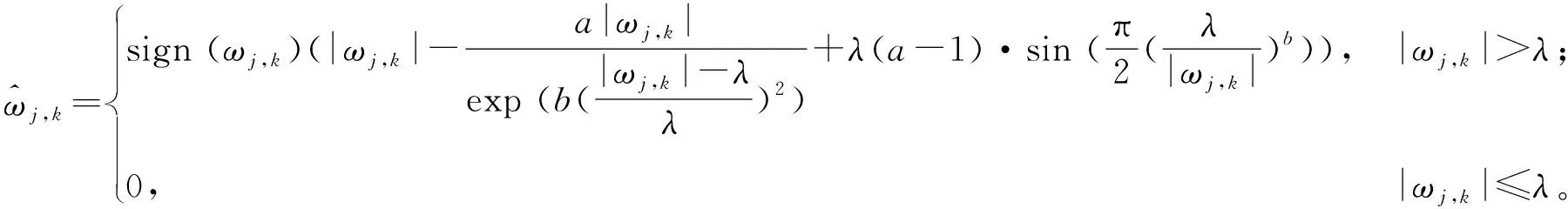
(3)
式中:a和b为调节系数,a∈[0,1],b>0。
图2所示为a和b取值不同时所得到的改进函数图像,可以看出当a值增大趋近于1时,函数的收缩愈紧,得到的小波变换系数ωj,k更接近于零;当b值增大,函数的收敛速度加快,更快地接近图像原始信号。因此可以通过调节a和b的取值灵活的调整阈值函数,使其具有更好的去噪性能。证明了课题组提出的改进阈值函数弥补了传统软、硬阈值函数的不足之处。

图 2 改进阈值函数图像Figure 2 Image of improved threshold function
2.2.2 改进阈值函数的可行性分析
1) 连续性分析
由式(3)可知改进的阈值函数为分段函数,分段函数的连续性问题只需要判定函数体在分段点ωj,k=λ和-λ处是否连续。
当ωj,k→λ+时,
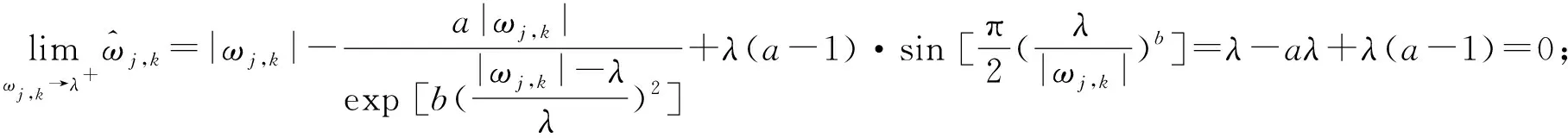
当ωj,k→λ-时,
表明该阈值函数在ωj,k=λ处连续。
当ωj,k→(-λ)+时,
当ωj,k→(-λ)-时,
表明该阈值函数在ωj,k=-λ处连续。故改进的阈值函数在(-∞,+∞)内连续。
2) 函数的渐近线分析
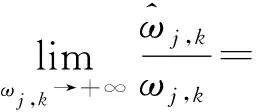



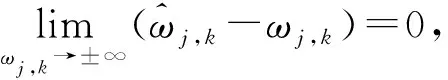
3) 函数的可导性

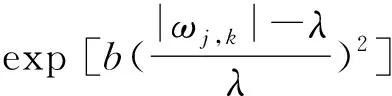

综上所述:课题组所提出的阈值函数克服了传统阈值函数的诸多不足之处,使得经过小波逆变换获得的重构信号和原始图像信号吻合度更高,理论上证明了该函数具有更好的去噪效果。
2.3 自适应阈值的选取
阈值λ的选取对于图像去噪性能的影响很大,选择合适的阈值可以在一定程度上改善图像的去噪效果。所选的阈值λ必须最大限度地将高频噪声的小波系数与初始图像信号小波系数区分开,通常阈值λ选取遵循VisuShrink准则。VisuShrink准则是采用固定阈值的方法,阈值
式中:σ表示噪声的标准差,L表示信号的长度。
σ是根据中值估计法得出:
式中:median(|Y(m,n)|)表示第1层小波高频分解系数的绝对中值,Y(m,n)表示第m层第n个小波分解的高频系数。
实际去噪过程中,当分解层数j增大时,高频小波系数逐渐减小。分解层数越大,剩余的小波系数均来自于原始图像信号,若此时依旧用固定阈值进行去噪,则会将原始图像信号中的部分小波系数置为零,去噪性能反而不佳,进而出现图像失真等问题。由于随着分解层数j的增加,在随后的每一层阈值都在相应地减小,课题组提出了一种自适应阈值:
(4)
式中:σ是噪声的标准差,j表示小波去噪分解层数,Nj表示第j层图像的大小,σj表示第j层图像噪声的标准差,λj表示当分解层数为j层时的阈值。
由式(4)可知,随着分解层数的增加,每一层的阈值都在相应地减小,这符合小波去噪的规律,故而可以提高小波去噪的性能。
3 图像采集和实验对比分析
3.1 退火图像的采集
金相图像采集的第1步是制备适合的试样。然后,需要用到计算机、金相显微镜、相机和图像处理软件等。为便于后续研究,对采集到的W18Cr4V退火图像进行裁剪并建立数据集。课题组参照GB/T 13298—2015《金属显微组织检验方法》,进行取样、磨制、抛光、金相显微镜采集和裁剪等操作,制备了3张不同区域且像素均为512×512 pixel的W18Cr4V退火状态下的金相试样,如图3所示。

图 3 W18Cr4V退火状态不同区域下的图像Figure 3 Image of W18Cr4V annealing state in different regions
3.2 实验对比与分析
为了验证课题组提出的改进阈值函数和自适应阈值算法的去噪效果进行实验。实验所采用的设备:Intel(R) Core(TM) i5-4210U CPU @ 2.40 GHz,内存8.00 GiB,Windows 10系统和MATLAB R2016a。测试图像为已采集的3张W18Cr4V退火状态图像。给3幅图像施加高斯噪声,方差为0.005。将加入噪声的3幅图像作为实验的去噪对象。选用小波基函数以及合适的分解层数对含噪图像进行小波分解处理。再用改进的阈值函数和自适应阈值处理后,对系数进行小波逆变换重构去噪后的图像。试验采用sym11小波基函数,分解层数j=3,新的函数中取a=0.7,b=10。将构造的新阈值函数、传统的软和硬阈值函数及文献[9]~[11]中提出的函数进行去噪性能比较,效果如图4~6所示。
由图4~6可以看出,使用改进的阈值函数和自适应阈值去噪后的效果更佳。但为了定量地分析去噪效果,课题组引入峰值信噪比RPSNR[15]和结构相似性MSSIM[16]作为评价指标:
(5)
(6)
(7)
式中:H,W表示图像的高度和宽度;X(h,w)是原始图像;Y(h,w)是含噪图像;EMSE为原始和含噪图像的均方差;C1,C2,C3为常数;μX,μY表示图像X和Y的均值;σX和σY表示图像X和Y的方差;σXY表示图像X和Y的协方差。
图像去噪性能与RPSNR成正相关;MSSIM大小不超过1,MSSIM值越大,表示图像与原图越接近。
表1所示为不同区域退火图像去噪效果对比。

图 6 退火组织区域3的去噪效果Figure 6 Denoising effect of annealed tissue region 3
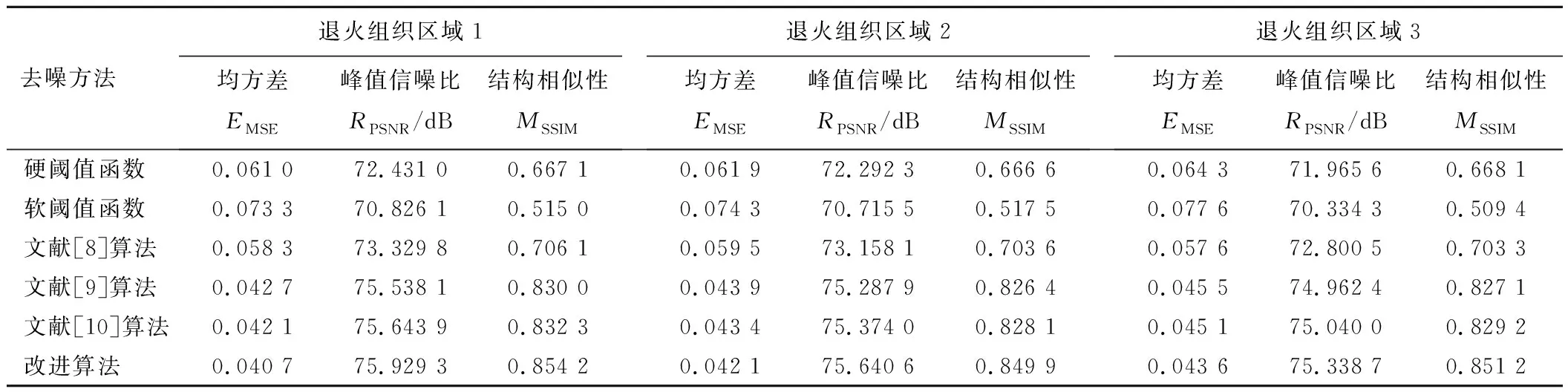
表 1 不同区域退火图像去噪效果对比
由图4~6和表1可知课题组提出的改进算法去噪效果与传统的软、硬阈值函数算法相比均有适当提升:退火组织区域1~3的改进算法的峰值信噪比RPSNR与传统的软、硬阈值函数算法相比分别提高了7.21%和4.83%,6.97%和4.63%,7.12%和4.69%;退火组织区域1~3的改进算法的结构相似性MSSIM与传统的软、硬阈值函数算法相比,分别提高了59.07%和28.05%,64.23%和27.50%, 67.10%和27.70%。课题组提出的改进算法与文献[9]、[10]和[11]中算法相比:退火组织区域1的改进算法的峰值信噪比RPSNR分别提高了3.55%,0.52%和0.38%,退火组织区域2改进算法的峰值信噪比RPSNR分别提高了23.39%,0.47%和0.35%,退火组织区域3的改进算法的峰值信噪比RPSNR分别提高了3.49%,0.51%和0.40%;退火组织区域1结构相似性MSSIM分别提高了20.97%,2.92%和2.63%,退火组织区域2结构相似性MSSIM分别提高了20.79%,2.84%和2.63%,退火组织区域3结构相似性MSSIM分别提高了21.03%,2.91%和2.65%。课题组提出的改进算法与文献[9]、[10]和[11]中算法相比,虽提升去噪效果不一,但也证明了课题组所提改进算法的有效性。

图 4 退火组织区域1的去噪效果Figure 4 Denoising effect of annealed tissue region 1

图 5 退火组织区域2的去噪效果Figure 5 Denoising effect of annealed tissue region 2
4 结语
因高速工具钢W18Cr4V退火状态下采集的图像内含有许多噪声,为更好地分割碳化物目标,需对采集的图像进行去噪处理。基于小波去噪的原理,课题组提出一种新的阈值函数小波去噪算法。该函数具有良好的连续性、可导性,且更逼近于原始图像信号;自适应阈值是随着分解层数的增加而自适应的减小,更符合去噪的实际情况。在MATLAB环境下对采集到的3张高速钢退火组织的金相图像进行去噪实验,试验采用sym11小波基函数,分解层数为3。试验结果表明:与传统阈值函数相比,改进的阈值函数对退火图像处理后所得峰值信噪比较高、结构相似性较好,去噪效果较好且自适应能力较强。
