基于模型的帕金森病闭环深部脑刺激效果指标研究

赵德春 陈 欢 沈利豪 焦书洋 蒋宇皓

①(重庆邮电大学生物信息学院 重庆 400065)

②(重庆邮电大学自动化学院 重庆 400065)

1 引言

帕金森病(Parkinson’s Disease, PD)是一种常见的神经退行性疾病，多发于中老年人。PD的临床症状主要表现为静止性震颤和运动迟缓等[1]。晚期PD患者生活无法自理，随着我国老龄化程度的加重，这将给社会带来沉重的压力。有研究表明，基底节为PD的主要致病区域，但是其潜在的致病机制至今还没有得到完美的诠释。目前以基底节中丘脑底核(SubThalamic Nucleus, STN)为刺激靶点的深部脑刺激(Deep Brain Stimulation, DBS)已经成为治疗晚期PD的一种常见的外科手术方式。但存在一定的局限性，比如电池能量消耗过快导致更换电池时会增加患者的开销与手术风险，患者的症状每时每刻都在波动，长期刺激可能会对人体产生如构音障碍、言语障碍等副作用[2–4]。如果能随时监测患者症状的波动并及时予以刺激，这不仅能节省电池的寿命，还会在提高刺激效果的同时减少副作用，由此推动了闭环DBS(Closed-loop DBS,CDBS)的发展。然而对CDBS算法的探索是一个漫长的过程，需要不断的研究试错才能最终应用于临床。但是直接以患者为研究对象是不可行的，同时以非灵长类动物直接进行实验不仅见效慢还会增加实验成本。因此建立以基底节为对象的计算模型，探索其与真实患者之间的内在联系，以及研究基于模型的CDBS算法有重要意义。

越来越多的证据表明，PD患者中丘脑底核局部场电位(SubThalamic Nucleus Local Field Potential, STN LFP)的β振荡(12～35 Hz)可以被持续检测到，并且其水平与运动障碍密切相关，是构建闭环DBS的理想反馈信号[5,6]。Peter Brown团队通过将β频段内的局部场电位(Local Field Potential, LFP)作为反馈信号，以丘脑底核(Sub-Thalamic Nucleus, STN)为靶点进行单侧或双侧刺激，成功获取了不同患者的实验数据[6–8]，证实了CDBS的有效性与可行性。相较于传统高频DBS,CDBS刺激效果提升了30%左右，能量消耗大约减少了50%，同时还减少了语言方面的副作用[7,9]。

Terman和Rubin等人[10,11]在2002年时建立了丘脑底核与苍白球外侧(SubThalamic Nucleus-Globus Pallidus external, STN-GPe)耦合模型以探索神经元之间的动态相互作用，并在2004年时将模型扩展为皮层-基底节-丘脑环路，此后的计算模型大多以Rubin和Terman等人建立的模型为基础进行改进，建立了更加复杂，更加符合PD患者脑神经活动的模型。但是其内部数学模型却不尽相同，比如常用的Hodgkin-Huxley方程[4]和Izhikevich方程[12,13]。基于模型的CDBS算法已经进行了广泛的研究，研究者一般采用丘脑中继准确度[14–16]、β频带功率[4,17,18]、能量消耗[4,14,16–19]等作为衡量CDBS的刺激效果，也有采用基底节中各神经元之间的同步性[12,17]作为评估指标。能量消耗是需要达成的目标之一，但在致力达到这个目标之前，需要保证刺激的效果。在临床上，不管是在药物治疗[5,19–21]，开环DBS还是为数不多的闭环DBS刺激研究中[6–9]，对治疗PD患者运动障碍的改善程度主要是通过患者填写的统一帕金森病评定量表(Unified Parkinson’s Disease Rating Scale, UPDRS)来进行评估。所以为了更直观，更加贴近临床评估效果闭环DBS的刺激效果，建立新的评估指标将UPDRS评分与基于模型的闭环DBS研究联系起来是有必要的。

对健康的非人类灵长类的动物研究中发现β爆发的时间动力学传递了重要的生理信息，即β爆发需要爆发[22]。在PD患者中也证实了这一点，Tinkhauser等人[6]通过对CDBS刺激后患者的数据从时域上进行统计分析，提出在CDBS刺激下持续时间较长的β爆发与运动障碍的改善程度呈正相关，持续时间较短的β爆发与运动障碍呈负相关的结论。Sun等人[23]也通过对CDBS刺激后PD患者的LFP从时域上进行特征提取，得到PD患者未刺激状态下的β频段有更多的长爆发而DBS状态下有更多的短爆发的结论。因此本文基于以基底节为对象的计算模型，从时域分析CDBS刺激下LFP的爆发特性，并与PD患者LFP数据的时域特性进行对比，研究其临床相关性。同时对β爆发持续时间的分类进行研究，提出与临床相关的指标，探索其作为CDBS刺激后用于估计运动障碍改善的可行性，为今后研究CDBS算法奠定基础。

2 方法

2.1 皮层-基底节-丘脑计算模型

基底节与人体运动控制等功能密切相关，基底节的损伤则是运动障碍疾病的生理基础，比如帕金森病。基底节接收来自皮层(Cortex, Ctx)的信息，并传递给丘脑(Thalamus, Th)。模型中的基底节(图1黄色区域为基底节)主要包括纹状体(Striatum,Str)、STN、苍白球外侧(Globus Pallidus external,GPe)、苍白球内侧(Globus Pallidus internal,GPi)。本文使用与Kumaravelu等人[13]相同的基于电导的皮层-基底节-丘脑模型，如图1所示，每类核团均包含10个神经元，每个核团之间的连接包含兴奋性连接与抑制性连接，根据网络之间的连接可以得到各神经元的膜电位方程，具体内容见文献[13]。该模型的正常状态，患病状态与STN DBS状态下基底节各神经元的神经振荡活动与平均放电率已经经过6-羟基多巴胺(6-HydroxyDopamine, 6-OHDA)损毁的大鼠实验进行了验证。

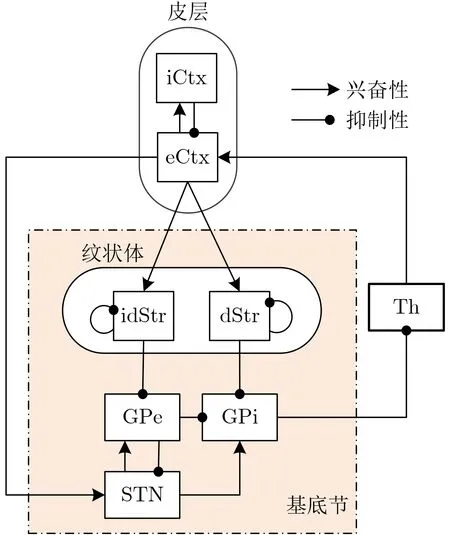
图1 皮层-基底节-丘脑网络模型

构建模型的主要目的是获取STN核团处的局部场电位(Local Field Potential, LFP)以进行下一步的研究，LFP计算公式为[24,25]

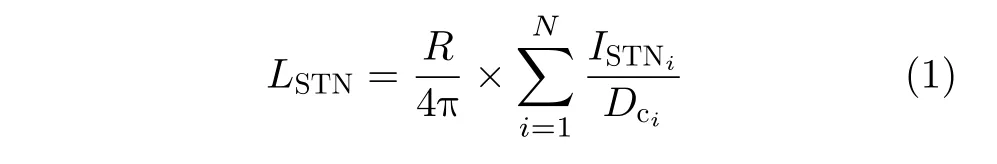
其中，R= 1 Ω·m 表 示均匀的细胞外电阻率，ISTNi为第i个STN神经元的总输入电流，Dci为 第i个STN神经元与中心记录电极之前的距离，假设每个神经元与刺激电极之间的距离相等Dci= 1 m m。

2.2 实验设置

在PD状态时，由于多巴胺能神经元的缺失，纹状体中M型钾离子电流减少，纹状体对接收皮层输入的敏感性降低，同时GPe内轴突侧支的突触强度加强，所以改变对应的参数即可模拟PD状态[13]。为了避免模型的偶然性对后续研究造成影响，通过改变参数的初始值模拟10名PD“患者”。有证据表明STN LFP中β频带的过度振荡与帕金森病的运动障碍密切相关[6]，所以在进行后续研究之前先验证模型的可行性。如图2为模拟的10名PD患者中Patient 2在LFP上β频带的功率，相较于正常状态，患病状态下的功率表现出了明显的急剧上升，特别在峰值范围内(19±4 Hz)。这很好地模拟了β频带的剧烈振荡，同时具有较好的鲁棒性。

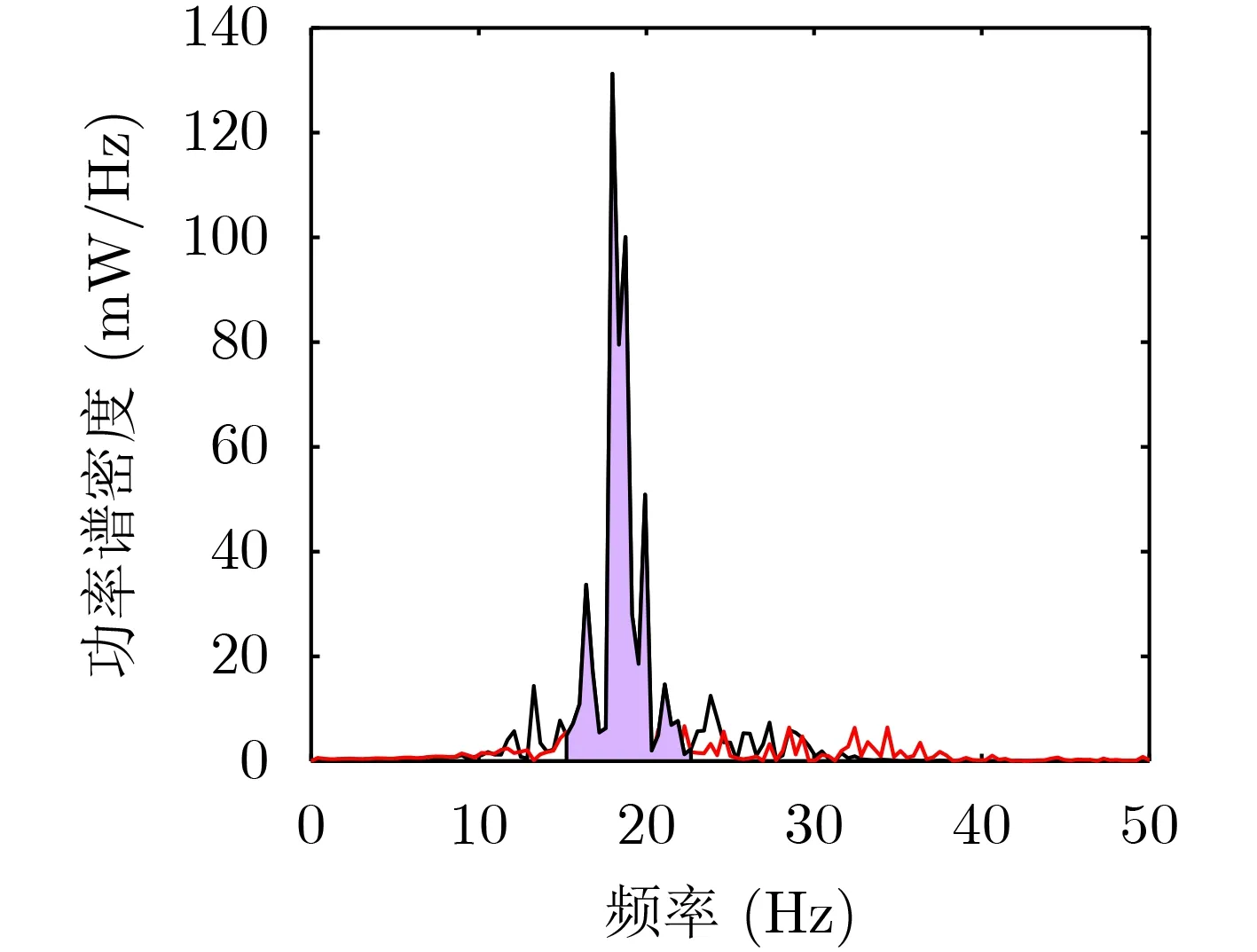
图2 LFP中β带功率谱密度

目前报道CDBS改善PD患者临床症状的研究者主要有Peter Brown团队，他们广泛采用的闭环控制策略为阈值刺激法[6–9]，接下来为了使研究更具有实际应用意义本文将以阈值刺激法为例进行后续研究。以往的研究表明，刺激阈值至少大于β振幅的50%时将具有良好的临床效果[6]，并且具体数值与患者的状况相关，因此本文随机选取大于β振幅52%分位处的数值作为刺激阈值。获取PD患者在未刺激状态下的LFP，并围绕β频段内的峰值活动频率范围进行带通滤波，然后包络以产生β振幅，通过计算获得PD患者在分位处的阈值大小为在线刺激提供参考。基于阈值控制策略的闭环DBS刺激如图3所示，首先获取未刺激状态下的LFP，然后在β频带的峰值频率附近进行带通滤波，接下来对β爆发进行包络以获得β振幅，结合在未刺激状态下得到的刺激阈值对β振幅的大小进行筛选，当振幅大于阈值时通过DBS波形发生器产生刺激波形对STN进行刺激直到振幅小于阈值才停止刺激。在开始刺激之前延迟时间为30 ms，同时为了避免神经组织受损，在真正的DBS外科手术中常采用电荷平衡双相脉冲[26]。所以本文采用脉冲宽度为100 μs，先阳极后阴极的130 Hz电荷平衡双相对称脉冲[8]。

获取每种状态下200 s的数据，然后使用Matlab2017a进行处理。对数据进行分析时为了提高计算效率，将数据降采样至200 Hz。在频域上，理论上DBS刺激应该能消除β频段的剧烈振荡，因此与图2类似，通过对比刺激与未刺激这两种状态下β功率的大小来评估刺激效果。在时域上，主要分析β爆发的持续时间与平均幅值的时域特性。首先将β爆发定义为从β振幅大于刺激阈值开始一直持续到小于阈值的时间段，如图3的红色椭圆框所示，而平均幅值定义为这段持续时间所对应的幅值的平均值。

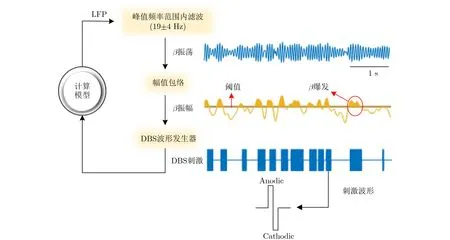
图3 闭环DBS刺激流程

在闭环DBS刺激期间存在频繁的刺激打开与停止的情况，刺激后的信号存在更大的方差[6]。对时域数据进行分析时，在相同百分位的阈值下β爆发的持续时间长短受不同状态下阈值大小的影响，所以为了避免低估刺激状态下的持续时间将阈值设定为两种状态下阈值的平均值，并将该阈值应用于所有状态。同样地，不同百分位的平均阈值也能影响爆发持续时间的长短，因此为了寻求不同阈值下数据分布的相似性，定义了不同百分位(55%, 60%,65%, 70%, 75%)的阈值。以65%分位下的阈值为例，图4为Patient 2在两种状态下持续时间与幅值分布的散点图，从中可以观察出β爆发持续时间的大小主要集中在500 ms以内。为了避免峰值频段以外的噪声影响，只保留大于100 ms的数据。但保留大于500 ms的数据也是有必要的，因为持续时间更长的突发变得越来越不频繁，并且未刺激状态下拥有更多更长的持续时间，其可能与PD症状的致病相关[6]。为了更加具体地研究不同爆发持续时间的分布情况，将β爆发划分为9个时间窗口以保证每个时间窗内都能拥有足够的β爆发个数。同时根据分布情况进一步将β爆发的持续时间划分为2个时间窗口以观察长爆发与短爆发的时域分布情况。

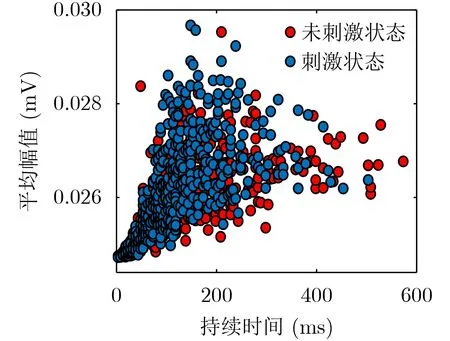
图4 65%分位阈值下β爆发时域图(Patient 2)

由于每名模拟患者β爆发的总数上都存在差别，所有数据均以平均值±标准差的形式出现，使用单因素重复测量方差分析数据之间的显著性，在此之前采用Kolmogorov Smirnov测试对数据进行正态分布检测，不满足正态分布的采用Wilcoxon秩和检验。

3 结果分析

不管是外科手术治疗[3]还是药物治疗[5]都会降低PD患者的β频带功率，因此在闭环DBS的算法研究中广泛采用β带功率的变化作为刺激效果的评估指标。而本文基于模型的阈值刺激策略也能显著降低β频段的功率(F=8.77, p<0.01) (图5)，所以本文应用的闭环刺激算法是可行的。

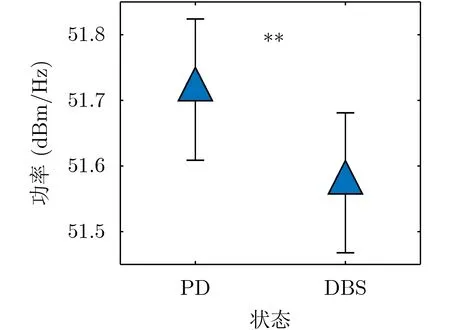
图5 不同状态下β频带的功率变化

图6为200 s的时间长度下两种状态β爆发的分布情况，图6(a)表明刺激状态下位于0.10～0.15 s的时间窗内β爆发数量显著多于未刺激状态(F=11.32,p<0.01)，相反的是在0.20～0.25 s, 0.30～0.35 s和大于0.5 s的时间窗内未刺激状态下β爆发的数量数明显多于刺激状态下的数量(F=7.14, p<0.05;F=7.27, p<0.05; F=5.28, p<0.05)，其中∗表示p<0.05，∗∗表 示p<0.01，∗∗∗表示p<0.001。结果表明与未刺激状态相比，DBS状态下短爆发(0.1～0.15 s)的数量更多，而长爆发(0.20～0.25 s,0.30～0.35 s和大于0.5 s)的数量更少。为了分析两种状态下爆发分布的具体差异，同时探寻不同阈值下β爆发分布的一致性，在相同条件下本文分析了所有阈值下β爆发的分布情况并总结得到了不同时间窗内β爆发的差值分布(图6(b))。这里∗表示所有阈值下存在显著性差异的时间窗，由于刚好在0.20～0.25 s的时间窗内刺激状态下的数量显著多于未刺激状态，所以本文进一步将时间窗二分类为0.10～0.25 s的短爆发与大于0.25 s的长爆发。

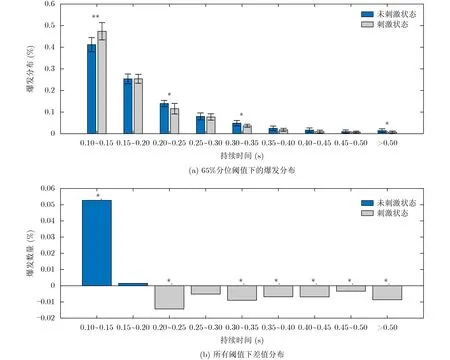
图6 β爆发的分布情况

如图7(a)，两种状态在二分类下的爆发分布具有显著性差异(F=11.32, p<0.01)，与未刺激状态相比DBS刺激下具有更多的短爆发和更少的长爆发，但是在总的爆发数量上两者却没有显著性差异(F=0.21, p>0.05) (图7(b))。同样在平均持续时间上也能得到相似的分布(图7(c)和图7(d))，即在总的持续时间没有显著性差异的情况下(F=4.4,p>0.05)，刺激状态下长爆发对应的总持续时间显著大于未刺激状态，而短爆发下则显著少于未刺激状态(F=10.58, p<0.01; F=8.74, p<0.01)，并且所有不同阈值下得到的结论一致。根据以往的研究经验，短爆发可能是人体产生的正常爆发，而长爆发可能是所谓的“致病”爆发[27]，PD症状的产生可能与此相关。结论表明CDBS能把未刺激状态下较长的爆发转移为更多较短的爆发，所以刺激状态下拥有更多的短爆发和更大的总持续时间，这有可能是改善PD症状的机制之一。

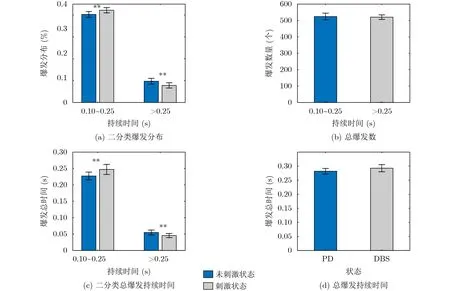
图7 65%分位下的β爆发分布

结合以往的研究经验，开环DBS和闭环DBS都能在一定程度上降低β带功率，虽然开环DBS降低的功率更多，但闭环DBS的改善效果更好[7]，所以在评估闭环DBS的刺激效果时单一地使用β功率或许不够全面。Tinkhauser等人[6]从时域分析得出β爆发的持续时间与UPRDS评分之间存在相关性，即持续时间较短爆发与运动障碍呈负相关，而持续时间较长的爆发与运动障碍呈正相关。也就是说较长持续时间的β爆发所占的比例越多，运动障碍相关的症状越严重，因此本文旨在研究相关的指标用于估计UPDRS评分。

根据UPDRS经过DBS刺激后评分可能会降低的特性，本文将估计指标定义为长爆发与短爆发之间的比值，并命名为UPDRS类估计(Similar to UPDRS Estimates, SUE)，即

其中，Ldur为持续时间较长的β爆发的数量，Sdur为持续时间较短的β爆发数量，这里长爆发与短爆发见图7(a)。

为了确认未刺激时SUE与持续时间之间是否相关，同时确认不同阈值之间的一致性，本文根据式(2)对所有阈值下的不同时间窗与SUE进行相关性分析。图8(a)表明在所有的阈值下SUE与持续时间较短的爆发呈负相关，而与持续时间较长的爆发呈正相关，示例如图8(b)和图8(c)所示。这和运动障碍与爆发持续时间之间的临床相关性所得的结论一致，因此初步认定SUE可用于估计运动障碍的程度(UPDRS-III第20, 22, 23项)。

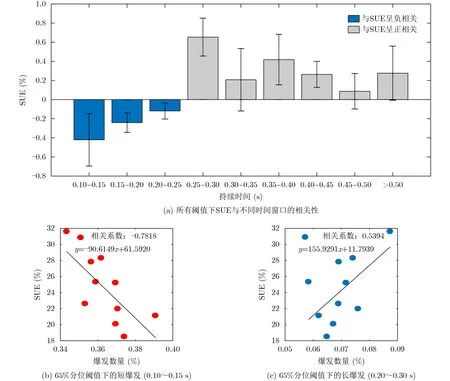
图8 持续时间与SUE之间的相关性

如图9所示，经过DBS刺激后SUE值显著低于未刺激状态下(F=18.42, p<0.001)，并且其改善效果较好，平均改善率几乎都能达到30%以上，这与实际情况相符，即经过有效的DBS刺激之后PD患者的UPDRS-III评分降低。然而有趣的是，从SUE的结果上来看模拟的10名患者中并不是所有的患者都对DBS的刺激有积极的响应，其中Patient 9的症状不仅没有得到改善，反而加重。产生该现象的原因可能是由于患者之间的差异性，如文献[6]描述的那样，每名患者达到较好的刺激效果时，所采用的刺激阈值是不同的。说明不适当的刺激阈值会加重患者的症状，从神经元的振荡方面来解释就是会增加长β爆发的产生。因此SUE不仅能很好地反映DBS刺激效果较好时UPDRS-III的变化，同时还能反映效果不好时的变化，表征患者之间的差异性。

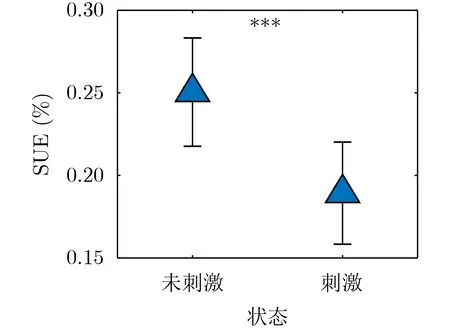
图9 不同状态下的SUE

4 结束语

本文以皮层-基底节-丘脑网络模型为平台，阈值刺激为闭环控制策略研究能够估计临床UPDRS评分的指标。首先通过频域内LFP β频带的功率变化验证了计算模型与闭环控制算法的可行性，然后在此基础上对比分析了LFP的时域特性，并提出了能估计在不同情形下动态变化的UPDRS-III指标。并且计算模型得到的β爆发持续时间更短，因此每个时间窗口的长度取较小值(50 ms)以保证充足的数据量。为了避免数据长度对结果产生的影响，分析了25 s和100 s的数据长度，得到了与200 s数据长度下相似的结论，阈值范围为55%～75%，并且在不同百分位阈值下数据分布一致性较高，能显著性地区分长爆发与短爆发。

在以往的研究中对计算模型有效性的验证往往是根据信号的放电率，神经元之间的同步性，或者丘脑中继准确度等指标。Sun等人[23]通过特征提取的方式验证了真实PD患者的刺激状态比未刺激状态拥有更多的短爆发，Tinkhauser等人[6]也经过统计分析得到了相似结论。本文通过在计算模型上进行的时域分析得到了相同的结论，该结论在频域的基础上更加符合DBS刺激状态下的真实特性，因此今后在对闭环DBS研究之前可以通过持续时间的显著性分布来验证计算模型与闭环刺激策略的可行性。

根据Peter Brown团队的研究结论，LFP β爆发的持续时间与患者的临床损害相关。该现象直接将人体信号的内部特性与外部表现联系了起来，而本文所提出的SUE指标能在一定程度上描述UPDRS-III在不同状态下的变化，将模型研究与临床效果相关，使得今后基于模型的闭环DBS算法研究更具有可靠性。此外通过时域特性分析表明阈值刺激法能通过抑制其可能“致病”的长爆发，诱导短爆发的产生来达到改善PD症状的目的。这或许是闭环DBS的治疗机制之一，因此基于模型的时域分析法也为今后探索闭环DBS的潜在治疗机制奠定基础。