水下近自由面爆炸过程中的多相流运动特性研究

余 俊，王海坤，刘国振，郝 轶，张得扬

（1.中国船舶科学研究中心，江苏无锡 214082；2.深海技术科学太湖实验室，江苏无锡 214082）

0 引 言

随着现代海战武器的高速发展，实战条件下舰船遭受的威胁越来越大，对舰船水下冲击与防护性能的研究受到了高度的重视。水面舰艇除了会遭受船底爆炸冲击损伤之外，近水面爆炸也会产生重要的威胁[1]。近水面爆炸现象的本质特征属于多相流体（气-液-汽）相互作用及其与结构的耦合运动过程，其非线性耦合效应主要体现在两个重要方面：首先是爆轰气体产物、水、空气等多组分流体之间的对流运动,其可归纳为多相可压缩流体界面捕捉问题；其次是自由面的存在使得流场中会出现稀疏波的传播，水中会出现典型空化现象,可以归结为相变问题。要想准确理解和掌握近水面爆炸过程中的多流体非线性耦合效应，需要同时重点处理好多相可压缩流体界面捕捉和相变问题。

目前国内外已经对近水面爆炸现象进行了大量的研究[2-4]。在实验研究方面，Marcus等[5]开展了水下近自由面爆炸试验研究，发现水下爆炸产生的片空化区域在闭合溃灭时会产生较大的压力，获得了近水面爆炸过程中包括空化效应的冲击波和气泡阶段的压力曲线;Brett等[6]开展了一系列水下圆柱壳近距离爆炸试验，对冲击波和空化联合加载下圆柱壳的变形进行了测量分析，发现空化载荷的幅值与冲击波幅值相当，而且空化溃灭载荷造成的壳体变形要超过整个冲击波阶段产生的总变形；Kleine等[7]利用纹影法拍摄到了近水面爆炸试验过程中液体空化的密度变化过程图象，较为清晰地展示了爆炸气泡膨胀以及空化域内部演化图像；Cui 等[8]开展了一系列不同边界条件下近水面小药量药包爆炸试验，获得了爆炸气泡与自由面运动的完整过程。由于实验研究获得的数据有限，在稳定性和重复性上难以满足要求，难以获得流场的精细特征。数值模拟能够较为全面地展示流场的精细特征，使得其在近水面爆炸研究中具有一定的优势。这里着重介绍基于多相可压缩流体计算模拟的研究情况，对于基于声学单元和边界单元的数值方法不作讨论。自从Aanhold 等[9]提出cut-off 空化模型之后，由于其使用简单方便，被广泛应用在水下近自由面或近结构爆炸分析中。Wardlaw等[10]利用cut-off模型分析了充水圆筒中心药包爆炸过程中冲击波在圆筒内部产生的局部空化现象，获得了空化溃灭载荷的典型特征；Shukla[11]、Yu[12]等采用cut-off 空化模型与五方程相结合的方法对带有空化效应的近水面爆炸多流体运动问题进行了研究；Wu 等[13]采用cut-off模型与流体局部间断迦流金（LDG）法相结合分析了水下远场冲击波与自由面作用产生空化的过程。为了克服cut-off模型无法描述空化域内液相和汽相组分的问题，Liu[14]、Schmidt[15]和Xie[16]等相继提出了isentropic 模型、Schmidt 模型和Modified Schmidt模型。这些模型本质上都属于单流体空化模型，在流体压力降低到饱和态压力之前均视为纯流体，当降到饱和态压力之后，各种模型的具体差别体现在空化域内汽液混合流体状态方程的构造方法不同。除了上述单流体空化模型之外，双流体模型也在不断发展，主要以Chiapolino[17-18]、Saurel[19]、Pelanti[20-21]等提出的四方程、六方程等模型为主，该模型通过持续追踪空化质量分数的演化来捕捉空化的产生、发展与溃灭过程。双流体模型则将初始流体视为液相和汽相的某种混合，在流场发生改变时（如冲击波传播和气泡运动等包含间断时）液-汽两相之间会发生对流运动，同时还伴随有质量和热量交换的相变过程，空化被视为流体区域内部蒸汽含量不断累积的过程。因此双流体模型描述的空化演化过程更符合物理本质和思维逻辑，但双流体模型相比单流体模型，双流体计算过程非常复杂繁琐，导致目前水下爆炸领域内绝大部分的空化研究都采用单流体模型。

本文拟采用Chiapolino 等[18]提出的基于多相可压缩流体四方程的双流体空化模型来重点研究近水面爆炸过程中的多相流运动。首先对计算模型的控制方程及其数值方法进行了简要介绍，然后采用一维激波管问题对计算模型中的相变转换以及激波捕捉功能进行了考核，最后针对近水面爆炸现象，将计算结果与试验结果进行对比，并重点分析空化域内部的典型物理特性。

1 计算模型简介

1.1 控制方程

不考虑粘性和热传导效应的多相可压缩流体运动方程可表示为[18]

式中，ρ、u、p和E分别代表混合流体的密度、速度矢量、压力和单位质量总能，E=e+0.5u·u，这里e为单位质量内能；Yk代表混合流体中各相介质的质量分数。控制方程（1）中参数k代表了混合流体中各相成分，为了计算模型中表达简便起见，这里约定如下：k=1代表液相成分；k=2代表蒸汽相成分；k=3,…，N代表其它不发生相变的气相或液相成分。本文中令k=3 代表空气（不可冷凝），k=4 代表爆轰气体产物。

在流体计算模型中普遍采用的是SG（Stiffed-Gas）状态方程，该方程能够描述多种液相或者气相流体的运动特性。近年来NASG（Nobel-Able Stiffed-Gas）状态方程逐渐被采纳，该方程修正了SG方程对液相介质中分子排斥力效应描述的不足[22]。该方程形式为

式中，ʋk=1/ρk、Tk、gk、ck分别代表k相流体介质的比体积、温度、吉布斯（Gibbs）自由能与声速，参数γk、、Ck、qk，qk'、bk等可以通过流体热动力学试验中与温度相关的饱和态压力、各相比体积、各相的焓等数据来拟合得到[22]。在饱和平衡态下液相与汽相的Gibbs 自由能相等，即g1=g2，化简可得饱和态下温度与压力的关系式：

式中下标“sat”代表饱和态，参数As、Bs、Cs、Ds、Es分别为

式中Cp,k表示第k相流体定压比热容。液态水、水蒸汽以及空气的NASG 状态方程参数如表1所示，其中W为物质的摩尔质量。本文算例涉及到水中空化问题所采用的计算参数均采用表1中的参数[22]。

表1 液态水、水蒸气和空气的NASG状态方程参数Tab.1 NASG coefficients for liquid,vapor and air

1.2 相变转换模型

控制方程（1）并未考虑到各相之间发生的相变过程，对于流体中发生液相与其对应汽相之间的物质与热量转换，可以参考化学反应过程中判断反应方向的判据，认为在达到平衡态之后液相及其蒸汽相之间的吉布斯自由能相等。同时结合控制方程（1）的假定，认为系统达到平衡态后满足如下关系式[18]：

将公式（2）和（3）代入，得

这里ppartial代表气体混合物中蒸汽相的分压，由公式可知其与蒸汽相的摩尔质量分数成正比[18]。非线性方程（6）～（8）可以采用迭代方法进行求解，如Newton-Raphson方法。

1.3 数值离散

控制方程（1）与状态方程（2）以及空化相变方程（6）～（8）共同构成了考虑相变效应的多相可压缩流体控制方程组，可以利用相变松弛法则进行分步求解[23]。第一步求解齐次双曲型方程组（1），需要结合状态方程（2），利用二阶MUSCL-Hancock方法以及HLLC近似黎曼求解器。通过该步获得中间变量（v,e,p,T,Yk）；第二步采用Newton-Raphson 迭代方法求得相变转换平衡态时的状态量（p*,T*,Yk=1,2）。

2 计算与讨论

2.1 一维激波管测试与验证

本算例主要用来与Chiapolino 等相同计算工况[18]进行对比验证。其中整个流场的蒸汽相初始质量分数设置为0.2，液相与气相的质量分数分别为0.1和0.7，计算域为[0,1]m。流场中密度和压力的初始间断面位于x=0.5 m，左、右侧压力分别为2×105Pa和105Pa，两侧密度分别为1.94 kg/m3、1.02 kg/m3。

图1 为t=1 ms 时刻流场中密度、压力、速度、温度、液相与蒸汽相质量分数分布曲线。其中P-T 和no P-T 曲线分别代表是否考虑相变转换时的计算工况，initial代表初始条件，Chiapolino 代表对比的数据（网格数为100）。同时为了考察计算模型的网格收敛性，分别采用100、200 和400 个网格单元均匀划分计算域。由密度和压力分布曲线可知，考虑液相和汽相之间的相变转换之后，向右传播的压缩波和向左传播的稀疏波的波速都稍有下降。由温度曲线可知，向右传播的压缩波波后温度在两种工况下都有所升高，但波后稳定区的温度在考虑相变转换时为346.3K,而不考虑相变时为362.6 K，差异较大。同理，向左传播的稀疏波波后稳定区的温度都有所下降，但是考虑相变转换后为344.7 K，而不考虑时则为329.4 K。这是由于在压缩波传播的波阵面以及稀疏波传播过程中液相与汽相发生了质量和热量交换，在达到平衡态的过程中温度存在变换。而汽-液两相的质量转换可以参考质量分数曲线得知，压缩波过后流体中液相发生了蒸发，使得汽相质量分数增加。该计算结果与通常理解的冲击波作用后由于压力升高容易引起液相发生冷凝的认识相矛盾，这里需要结合温度变化进行联合分析。由于考虑了相变转换，冲击波作用后波后温度由初始的337.5 K 上升到346.3 K,虽然波后压力也由初始的105Pa上升到1.4×105Pa，但是从饱和态曲线P-T（公式（3））来分析会发现温度升高引起的蒸发效应要大于压力升高带来的冷凝效应，最终效果就是压缩波后处于蒸发状态。同理，向左传播稀疏波的最终效果是波后处于冷凝状态。由图1 可知，随着网格数的增加，计算结果的收敛性较好，本文的计算结果与Chiapolino的结果吻合较好。

图1 1 ms时刻流场各物理量分布曲线图Fig.1 Diagram of different variables in fluid at t=1 ms

2.2 水下近自由面爆炸现象

本节利用上面介绍的计算模型与Cui 等[8]的试验观察结果进行对比。该试验在边长2 m 的立方体水槽内开展，采用等效于5.2 g TNT 的药包起爆，药包中心位于水下0.13 m 处。药包采用等效爆轰模0.0型09近m似，爆处轰理气，根体据产G物e内e r-部H密u n度ter和理压论力模分型别[24]以为及16数06值kg经/m验3和，初10始9P球a，形采爆用轰理气想体气产体物状半态径方设程置，γ为=1R.80=，CV=695，W=290。空气、水和爆炸气泡内的初始蒸汽质量分数分别为10-9、10-8和10-6。空气、水和爆炸气泡的初始温度分别设置为295 K、295 K 和1120 K,其中空气和爆轰气体产物处于过热状态，水处于饱和状态。空气、水和爆炸气泡内的初始蒸汽体积分数分别为1.56×10-9、1.39×10-5和8.07×10-7。为了节省计算资源，采用二维轴对称模型进行模拟，如图2 所示。其中y轴为对称旋转轴，y=0 为初始水平面位置，药包位于(0,-0.13)m处。计算域采用非均匀结构性网格划分，如图2 所示（图中显示的网格密度为实际的1/2）。其中区域[0, 0.4]×[-0.6, 0.2] m2内采用均匀网格，dx=dy=0.001 m，区域外采用等比数列格式的递增步长网格，等比为1.02。整个计算域网格为650×1200，计算域大小为[0,7.34]×[-7.5,1.1]m2。y轴边界设置为对称条件，其它如空气层上方、水域下方以及右侧边界均设置为无反射条件，CFL设置为0.5。

图2 近水面爆炸二维轴对称计算模型与网格划分示意图Fig.2 Schematic of 2D axisymmetric model and mesh size of underwater explosion near free surface

图3 显示了在考虑相变条件下t=0.084 ms、0.168 ms、0.334 ms、0.5 ms、0.666 ms、1.0 ms、4.176 ms 和6.176 ms 时刻流场中的密度、压力和蒸汽体积分数分布云图，其中所有图片采用统一大小的观察窗，尺寸为[-0.6,0.6]×[-0.7,0.35]m2。由于图3 中的各物理量的内部分布跨度非常大，未单独列出各云图的刻度线，压力云图中的黑色虚线表示对应时刻爆炸气泡界面的位置。0.084 ms 时刻，初始冲击波刚到达自由面不久，其产生的反射稀疏波使得自由面下方附近出现蒸汽聚集，图中对应时刻蒸汽体积分数云图显示的局部高亮区域内数值范围为0.4‰～2.5‰。随着稀疏波不断向下传播，0.168 ms 时刻稀疏波已经达到爆炸气泡上壁面，并反射压缩波，可以发现此时爆炸气泡表面附近的局部范围处于相对高压区。随着稀疏波在爆炸气泡表面反射成压缩波以及自由面不断反射稀疏波，旋转轴上的蒸汽含量不断降低（对应空泡溃灭过程），而旋转轴外侧的蒸汽含量不断增加（对应空化产生过程），如图3中的0.334 ms和0.500 ms所示。随着空泡的不断产生和溃灭，空泡中心区域逐渐变薄，并向外扩张，如图3中的0.666 ms和1.0 ms所示。在4.167 ms和6.167 ms时刻空泡基本上完全消失，但爆炸气泡一直处于向外膨胀过程，并不断抬高水面位置。在整个过程中空化由开始的单连通域不断演化为多连通域，显示出涡环形状，涡环逐渐向外扩展，并逐渐变薄直至最终完全消失。

图3 典型时刻流场的密度、压力和蒸汽体积分数分布云图Fig.3 Contour plots of the density,pressure and vapor volume fractions at typical times

在上述整个时间段内，自由面上方附近的空气中蒸汽含量一直比较高，并且包含蒸汽的区域不断扩展。这是由于水中初始冲击波作用自由面后向空气透射压缩波、水中的液相和汽相同时向空气中扩散的结果，在扩散过程中仍然存在液-汽两相之间的相变转换。这是因为水面上方初始空气中是不包含液相水，而且水蒸汽含量极低（10-9），而图3中蒸汽体积分数云图中红色区域代表自由面上方，其内部的液相水的质量分数范围在0.6～0.8，水蒸汽质量分数范围在0.1～0.3，剩下的为空气。

文献[8]中只记录了通过观察窗获得的部分流场图像，如图4 中第一行所示。试验获得的图片的中间纵剖面尺寸与数值模拟中的[-0.4,0.4]×[-0.68,0.2]m2基本相当。在第一行的试验图片中左下角两位数值代表图片序号，右下角为记录的时刻（单位为ms），其中0.167 ms代表装药起爆时刻。由图4可知，小药量装药在近水面爆炸时在水面下方产生的空化域形态与“云空化”非常相似，水中的空泡体积非常小，形成云带状，其发展过程中能够观察到明显的涡环形状。为了与试验进行对比，需要对“云空化”区域内的蒸汽含量进行判断，选取蒸汽体积分数是一个比较合适的对象。这里假定当流体单元中的蒸汽体积分数大于0.5‰时就标记为空化单元，单元所在的区域即为空化域。有关空化域内蒸汽含量的判据目前仍然没有统一的标准，这里选取的0.5‰只是数值计算上的一个参考。将图3 中蒸汽体积分数云图转换为空化域纹影图，如图4 第二行所示。其中红色区域为水下空化域，黄色区域为自由面上方的高含量蒸汽集中区域，绿色为空气，蓝色为水域，浅蓝色为爆炸气泡。经过对比可知，计算获得的水中空化域与试验观察到的“云空化”范围基本相当，两者都清晰地展示了空化域形成涡环，并逐渐向外扩张和变薄的过程，最终完全溃灭。

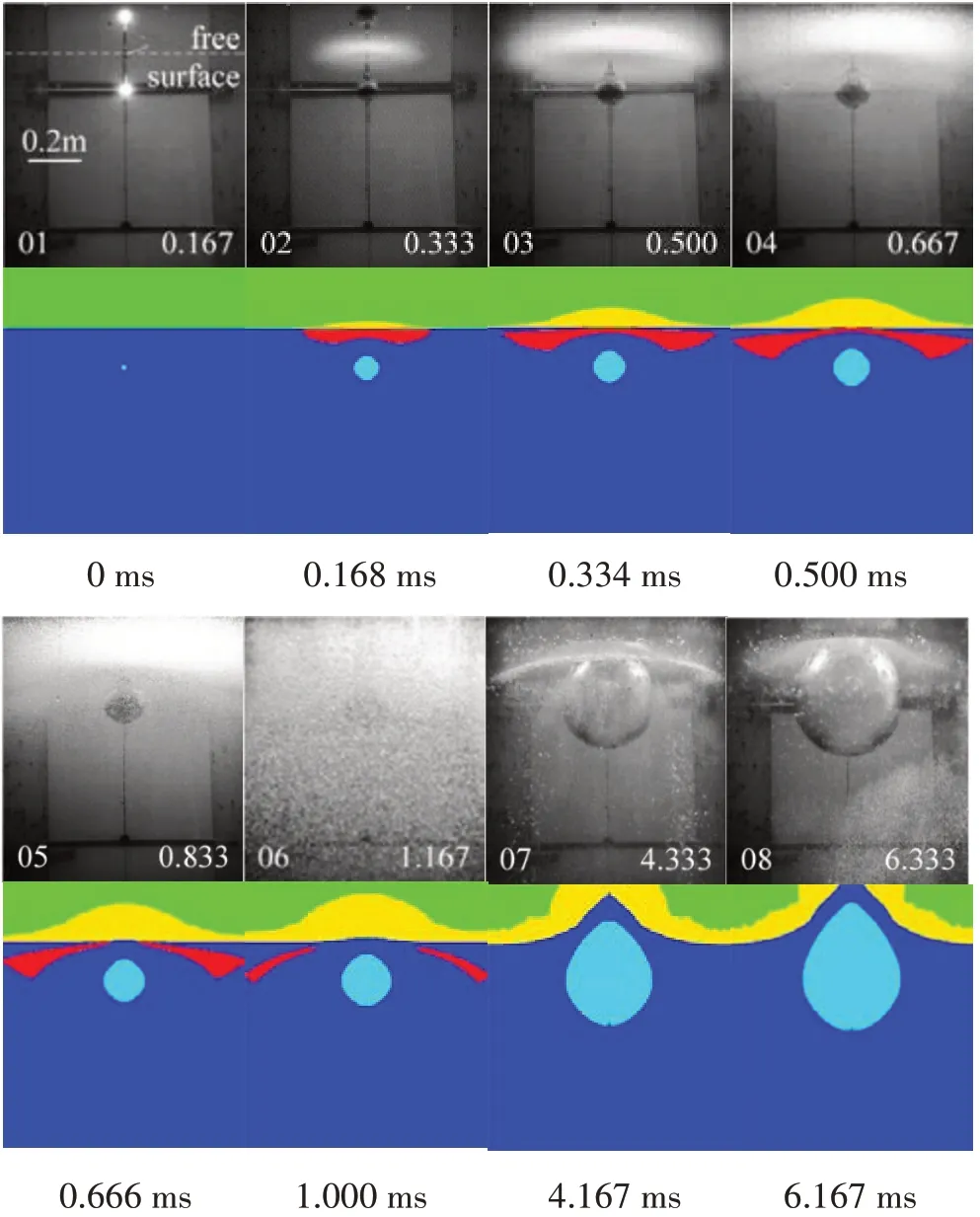
图4 典型时刻的试验与计算结果对比Fig.4 Comparison of experimental and numerical results at typical times

图5 显示了空化域内的最大、最小和平均温度变化以及空化域总体积时程曲线。由图5 可知空泡总体积的膨胀过程与收缩过程的时间基本相当，整个空化运动周期约为1.14 ms。空化域膨胀和收缩过程中内部最高温度变化范围为294.6～309.7 K，最低温度变化范围为283.7～294.6 K。膨胀到最大体积时空化域内部的最高和最低温度分别为309.7 K 和283.7 K，但在空化域变化过程中其内部体积平均温度基本恒定为294.6 K，与室温相当。

图6 为流场中三个坐标点处压力时程曲线图，分别为水下0.05 m 处距离爆心不同水平距离处的测点。由图可知，三个测点处的空化溃灭过程中最大压力分别为2.15 MPa、0.98 MPa 和0.92 MPa。图7 为空化域内最大、最小和平均压力变化时程曲线。由图可知，空化域内最大压力在体积膨胀阶段的大部分时刻保持在0.018 MPa 左右，而在收缩阶段则主要在0.018 MPa 上方振荡，最大值达到0.029 MPa。空化域内最小压力在中间的绝大部分时间内变化较为平缓，在3200～4800 Pa 范围内变动，只是在空化刚开始产生和最后溃灭阶段变化梯度较大。空化域内体积平均压力变化范围为9000～18 000 Pa，其变化趋势与最小压力变化趋势基本保持一致。由此可见，空化域内压力并不是维持在饱和态压力不变，其具有分布不均匀性、变化梯度大等特点。同时结合图5可知其内部温度的变化范围在283.7～309.7 K，空化域内部发生较为明显的相变转换现象。

图5 空化域内最大、最小和平均温度以及空化域体积的时程曲线Fig.5 Time history of the maximun,minimun,average temperatures and cavitation domain volumes in cavitation domain

图6 三个测点处压力时程曲线图Fig.6 Time history of pressure at three measuring points

图7 空化域内最大、最小和平均压力时程曲线Fig.7 Time history of the maximum,minimum and average pressures in cavitation domain

图8 为空化域内的蒸汽相体积分数的最大和平均值变化时程曲线，空化域内蒸汽相体积分数的最小值为前面设定参考值的0.5‰。由图8 可知，空化域内的蒸汽相体积分数在0.5‰～173‰，其峰值并未出现在空化体积膨胀到最大的时刻。尽管空化整个运动过程中蒸汽相最大体积分数并不低，但是空化域内部整体体积平均值变化区间在0.5‰～10‰，说明蒸汽的平均含量比较低，这与前面介绍的实验中观察到的“云空化”较为一致，同时也说明了本文计算模型具有一定的合理性和精确性。图9为空化域内密度的最大、最小和平均值变化时程曲线。由图9可知，空化域内的最大密度变化范围为1051～1061 kg/m3，体积平均密度变化范围为1039～1051 kg/m3，最小密度变化范围860～1061 kg/m3，其峰值也未出现在空化体积膨胀到最大的时刻。结合图8可知，空化域内蒸汽相的含量总体上非常小，对于流体密度降低的程度有限，空化域内总体体积平均密度变化较小。

图8 空化域内蒸汽体积分数ϕ2最大值、平均值变化曲线Fig.8 Time history of the maximum and average vapor volume fractions ϕ2 in cavitation domain

图9 空化域内密度的最大值、最小值和平均值的时程曲线Fig.9 Time history of the maximum,minimum and average densities in cavitation domain

3 结 论

针对近水面爆炸过程中出现的爆轰气体产物、水以及空气等多流体复杂运动，以及各种流体内部可能出现的液相水和汽相水之间的相变转换等现象，本文采用了基于相变效应的多流体运动计算模型进行处理，获得了如下结论：

（1）利用一维激波管问题对计算模型精确性和收敛性测试表明，本文的模型计算结果与Chiapolino的结果吻合较好，能够精确地捕捉冲击波与稀疏波的传播过程，展示了冲击波作用之后流体蒸发以及稀疏波作用之后流体冷凝的过程，最终的状态往往是两种过程的综合作用的结果；

（2）近水面爆炸过程中爆炸气泡运动过程的计算结果与试验结果符合较好，说明本文建立的多流体耦合计算模型能够捕捉多种界面之间的复杂运动过程。

（3）多流体计算模型中引入了相变转换，可获得近水面爆炸过程中水面下方的液体内部发生的空化现象；采用蒸汽体积分数0.5‰作为空化域识别的判据，数值模拟获得的空化域范围与试验结果较为一致，空化域都是由开始的单连通域演化为涡环形态，并向外扩展直至完全溃灭。

（4）数值模拟结果发现，空化域在运动过程中其内部蒸汽的体积分数范围为0.5‰～173‰，但内部平均值的范围仅为0.5‰～10‰，说明蒸汽的平均体积含量比较低，这与实验中观察到的“云空化”现象具有一致性。同时该现象也可以从空化域内部密度的平均体积含量来得到印证，其变化范围为1039～1051 kg/m3，说明空化域内部平均密度与常态下液相水的密度非常接近。另外，空化域内的压力变化范围为3200～29 000 Pa，温度变化范围为283.7～309.7 K，说明空化域内部的压力和温度一直处于动态变化之中，并不是维持在某个恒定的饱和态不变。

近水面爆炸过程中除了存在多流体之间的非线性耦合效应，还会与周围结构发生流固耦合作用，其过程更加复杂，将在后续计划中研究。