基于LSTM 和BP 神经网络模型的净初级生产力预测

于明洋，魏霖静

（甘肃农业大学理学院，兰州 730070）

0 引 言

由于工业技术的不断进步以及人类城市建设步伐的加快，人类的活动对于全球生态系统所造成的影响正日益增强，也随即导致了全球气候变暖、极端气象灾害频繁发生和海平面有所升高等一系列问题。 作为人们生存和发展所依赖的系统，对气候变化这一大背景下的陆地生态系统变化进行研究已逐渐成为关注热点。 植被是陆地生态系统的主要组成部分，在全球气候变化中起着非常重要作用。 植被作为气候变化和人类活动最重要的影响要素之一，是人类生存离不开的物质和环境主体之一，也是链接土壤和承载水系的重要节点，因此关于植被如何响应全球气候变化也是需要研究的核心问题。

植被生产力对人类自身的日常生活和经济发展产生着重要影响，同时也是各种人类活动中至关重要的基础资源。 净初级总产量（Net Primary Productivity，NPP） 是指从总产销量减去植物呼吸的需求量后剩下来的总量；也指特定时间内，经植株的组织形式或贮存产物的形态所表达而蓄积出来的有机物的总量。NPP是指示植被环境运动的重要因素，体现了生态稳定CO2的功能。NPP与异养循环速度的均衡（即净生态系统生产，NEP）则确定了是否有微生物环境中对过量大气CO2的积累，是大气环境中CO2含量季节变动的主要因素。 通过正确地计量NPP，可以认识全球碳循环的基本过程。 另外，NPP也是对陆地生态系统中营养物质和能源平衡运转研究的重要基础。 除供应了水生植物本身之外，还为整个有机体生活提供了能源和物质基础，因此对陆地NPP的研究也为人们合理开采、使用资源提供了依据。

植物不断进行的光合作用为生态系统的运行提供了大量的能量，对于地球上的大多数生命来说这都是不可缺少的一部分。 至今人们对于研究陆地植被净初级生产力的变化已经有很长的时间，但是大规模的工作则于20 世纪60年代开始［1］。 上世纪七十年代中，Lieth［2］在计算时逐步构建了首个覆盖全球范围的NPP 回归模型，并在此基础上模拟世界NPP 的地理分布，从而给出了首张全球NPP 的分布图，同时又通过大量研究证明了植被世界NPP 是每年降雨量与年平均气温一致的地区函数［3］。

植被净初级生产力是植物生态过程调控的关键指标，在碳平衡与全球变化过程中起着关键性的影响作用［4］。 根据植被净初级生产力来确定生态系统的安全与否［5］，Rashid 等［6］指出，植被NPP并不只是对地区生态演变进行评价的主要指标体系，还在研究碳循环过程中贡献了关键的组成模块，同时也与研究陆地生态系统固定碳能力有关的强弱有着关系。 研究植被净初级生产力已经成为研究气候因素和人为因素对陆地生态系统的影响中必不可少的一项内容［7－8］。 近年来的研究表明，中国国内的专家反演出对几十种NPP 的模式。 例如，孙政国等学者［9］利用BIOME－BGC 模型对中国南方不同草地类型的NPP进行了评估，发现位于南部区域的低山丘陵草地、常见草山草坡以及高山草甸的NPP与净生态系统生产力（NEP）的变化有着差异。 Li 等学者［10］研究了内蒙古草原植被生产力与SPEI 指数之间的相关关系，发现水分对内蒙古草原生产力的变化起主要作用。 国内研究者也通过各种手段对全国及地方的净初级生产力水平展开了深入研究，涉及Theil－SenMedian 趋势分析、多重共线性检验、多元回归分析、残差研究和偏自相关分析等传统统计研究方法［11］。 目前研发了CASA 模型［12］、RBF 神经网络［13］、Biome －BGC 模型［14］、C －Fix 模型［15］、MIAMI 模型［16］等，这些模式都可以较为精确而详尽地说明植物发育的历程，对NPP的评价也具有很大的可信度。 然而，这些模型无法很好地把握NPP随时间的变化特征，缺少对于其时间维度方面的分析。因此，需要一种捕捉其序列特征的方法来改进目前的算法，以利于更好地对NPP 进行预测。

近年来，反传播式（Back Propagation，BP）神经网络算法和长短期记忆神经网络（Long Short Memory，LSTM）已经被应用于很多领域来解决分类和预测等问题，也有很多研究者把LSTM 应用于时间序列数据的预测，并且得到相比之前方法更高的准确率［17－19］。 所以，可以采用LSTM 和BP 的神经网络模式，通过气温、 雨量、 归一化植被指数（Normalized Difference Vegetation Index，NDVI）作为影响因素对NPP进行预测。

1 模型原理和方法

1.1 BP 神经网络

BP 神经网络算法［20］是一个采用误差反传播方法进行的多层前馈网络系统，是目前使用最普遍的一种神经网络模式。 BP 网络能够用于了解并保存大规模的投入与输出模式的反映关联，并且不要求学校预先公开关于这种反映关联的数学教育过程。其基本方法是选择最陡峭的下降法，并采用反向方法来调控网络的权重值和阈值，从而获得最低误差平方和。 BP 神经网络方法已经应用在非线性建模、参数逼近、系统辨识等领域，且有众多研究者对其进行了改进［21－23］。

在实际问题中，BP 神经网络模型结构需由实验确定，无规律可循。 一般情况下的神经网络都先期设置好了上网的层数，而BP 网络系统也可能具有各种各样的隐层。 理论上也已证实，在不影响隐含节点数量的情形下，对2 层以上（仅有某个隐层）的BP 网络，能够进行随机本构非线性映射。 在模拟样本相比较少的情形下，较少的隐层节点也能够进行模拟样本空间的超平面分析。

一个通用的BP 神经网络架构如图1 所示。 这里，输入数据可以描述为X＝（x1，x2，…，xn）T；进入输入层后，将其和权重向量W1＝（w1，w2，…，wn）T进行位置乘积后，再通过激活函数就可以获得下一级的输入向量；隐藏层的层数t确定后，每层的输入和输出都与输入层的操作一致，但隐藏层的每一级神经元数量却可能和输入层有所不同；因此，最终将隐藏层的输出视为输出层的输入，经过权重向量的乘积后可以得到输出数据Y ＝（y1，y2，…，ym）T。 整体流程可以表示为：

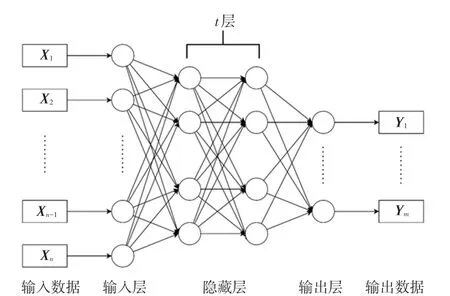
图1 BP 神经网络结构图Fig. 1 Neural network structure diagram

（1）输出层

（2）隐藏层

1.2 LSTM 神经网络

长短期记忆（LSTM）［24］是一款已应用在人工智能和深度学习领域的人工神经网络。 和标准的前馈神经网络有所不同，LSTM 有反馈接口。 这样一来，循环神经网络（RNN）不但能够管理一个数据点（如图片），还能够管理一个数据序列（如话音或录像）。也因此，LSTM 已广泛应用在非分割、连接的手写辨识、语音识别、机械翻译、机器人操控、视频游戏、和医疗保健等任务中［25－29］，现已成为20 世纪被引用最多的神经网络。

LSTM 的名字是指一个标准的RNN 同时具有“长期记忆”和“短期记忆”的比喻。 网络中的连接权重和偏差在每级训练中改变一次，类似于突触强度的生理变化如何存储长期记忆；网络中的激活模式在每个时间步中改变一次，类似于大脑中电击模式的瞬间变化如何存储短期记忆。 LSTM 架构旨在为RNN 提供一个可以持续数千时间步的短期记忆，因此是“长短期记忆”［30］。

一个LSTM 单元由一个单元、一个输入门、一个输出门，以及一个遗忘门所构成。 单元可以在任意的时钟间隔内的数值，通过3 个门调节一个进出单位的数量。 LSTM 的基本结构如图2 所显示，其整体流程可以表示为：

图2 LSTM 结构图Fig. 2 LSTM structure diagram

其中，Wq、Uq表示输入门与递归连接的权重，q可以是输入门i、输出门o、遗忘门f或记忆单元c。

LSTM 系统适用于基于时间序列信息的分析、管理与估计，但在时间序列中的关键事件之间可能具有未知的滞后时间。 原始的RNN 系统在训练时，由于训练长度的增加和网络层数的增多，会产生梯度弥散爆炸或局部梯度消失的现象，使得系统无法处理更长序列信号，也因此无法得到更长距离数据的信号。 针对这一状况，提出了后续的改进方案、即LSTM 神经网络。 LSTM 神经网络在深入学习后可以更好地处理序列化数据分析问题，其对于发电负载、流量等预测都有着不错的预知效果。 LSTM 用于了解时间的中短期相关数据，因为神经网络中含有时钟记忆模块，所以适合于分析和检测时钟序列中的间隔和延迟事件［31］。

1.3 激活函数

激活函数的引入主要是为了提高神经网络模型的不确定性，因为没有激活函数时每层就等于矩阵的相乘。 任何一级输入／输出都是最上层的系统的线性函数，所以不论在神经网络哪一层，输入与输出都是系统的线性组合，也都是最本原的感知机。 通过加入激活函数，为神经元导入非线性参数，神经网络就能够逼近一个非线性函数，而这种神经网络也能够运用在多种非线性模型上。 本文采用的激活函数有3 种：ReLU、Sigmoid（σ） 以及tanh。

1.3.1ReLU

在人工神经网络的背景下，ReLU（Rectified Linear Unit）激活函数是一个定义为其参数的正部分的激活函数。ReLU函数的定义公式为：

其中，x是神经元的输入。 这又被称作斜率函数，类似于电气工程中的半波整流。

该激活函数从20 世纪60年代末开始出现在分层神经网络的视觉特征提取中，并有专家认为该函数有着很强的生物学动机和数学理由。 本文分析后发现，与在2011年以前普遍采用的激活函数比较，该激活函数可以更好地使用在更深的系统，包括logistic sigmoid（受概率论启发，见logistic 回归）以及要比logistic sigmoid 更实际的对应函数方法、即双曲正切中。 研究可知，该激活函数主要具有以下3 个优点：

（1）稀疏的激活。 在一个随机初始化的系统中，有大概50%的隐藏单元被触发（有一个非零输出）。

（2）更好的梯度传递。 与双向饱和的正弦波激活函数一样，更少出现梯度消失问题［7］。

（3）高效的计算。 只有比较、加法和乘法。

1.3.2Sigmoid

Sigmoid函数是一个具有＂S ＂形特征曲线的逻辑函数，其定义为：

在某些领域，特别是在人工神经网络方面，“Sigmoid 函数”一词被用作logistic 函数的别名。

Sigmoid函数的其他情形，包括Gompertz 曲线和Ogee 曲线Sigmoid函数的值域也为实数，返回值（响应）通常是单调增长的，但也可能是下降的。Sigmoid函数最常显示的返回值（y轴）在0 到1 的范围内。 另一个常用的范围是－1 到1。

1.3.3tanh

在几何上，双曲函数也是普通三角函数的近似物，但用双曲线并没有相应的基本概念。 即如点（cost，sint） 构成单位半径的圆一样，点（cosht，sinht） 构成单位双曲线的右半部分。 另外，与sin（t） 和cos（t）的导数分别为cos（t）和－sin（t）相似，sinh（t） 和cosh（t） 的导数分别为cosh（t） 和＋sinh（t）。

双曲函数出现在双曲几何的角度和距离的计算中。 同时也出现在许多线性微分方程、三次方程和直角坐标的拉普拉斯方程的求解中。 拉普拉斯方程在物理学的许多领域都很重要，包括电磁理论、热传递、流体动力学和狭义相对论。

tanh 是由基础的sinh 与cosh 计算得来，其定义式为：

2 实证分析

2.1 数据集来源与处理

文中选取的4 个数据、即3 个相关因子：气温、降水、NDVI，以及所要预报的NPP值。 气温和降水数据均采用了兰州市气象局资料，NDVI采用的是MOD13C2，而NPP则采用的是北纬18°以北的土地生态系统，逐年净初级生产力1 km 的栅格数据集（1985－2015）［32］。 选取的时间为2001年1月1日到2015年12月1日。

在开展试验前，必须对样本进行预处理。 此次试验，把数据集中按照8：2 的标准分类成了训练集和测试集。 将数据集中输入后，先对数值进行归一化处理，并测试是否出现了异常数值和缺失数据，上述步骤完成后才能进入下一步。 本研究的样本集经检测均未产生异常值和缺失值，故不要求对其做幅值归一性处理。 信息的归一化能够使各种信息的计量单位一致，而且能够增加模型的准确性。 进行归一化分析的方法见式（5）：

其中，xi为第i个变量；为xi的均值；max（x），min（x） 分别表示xi的最大值和最小值。

本文选取SSE、MSE、RMSE、MAE、MAPE、SMAPE作为2 种神经网络预测模型性能的评价指标。 其中，SSE、MSE、RMSE、MAE、MAPE、SMAPE的数学定义及表述详见如下。

（1）和方差SSE（the Sum of Squares Due to Error）。 是观测值（Observed Values） 与预测值（Predicted Values）的误差的平方和，定义公式为：

（2）均方误差MSE（Mean Squared Error）。 是观测值（Observed Values）与预测值（Predicted Values）的差值的平方和的平均数，即SSE／n。MSE是误差的二次矩，是估计量的方差（Variance）及其偏差（Bias），是衡量估计量质量的指标，定义公式为：

（3）均方根误差RMSE（Root Mean Squared Error），也称作RMSD（Root Mean Square Deviation），是MSE的算数平方根。 由于每个误差（Each Error）对RMSD的影响与误差的平方（Squared Error）成正比，因此较大的误差会对RMSE影响过大，RMSE对异常值很敏感。 其公式为：

（4） 平均绝对值误差MAE（Mean Absolute Error）。 是时间序列分析中预测误差常用的指标，由于MAE使用的是与被测数据相同的尺度（Scale），因此不能用于比较2 个不同尺度的序列。MAE又被称为L1 范数损失函数（就是可以作为损失函数），是真实数据与预测数据之差的绝对值的均值。 定义公式为：

（5） 平均绝对值百分比误差MAPE（Mean Absolute Percentage Error），也被称为MAPD（Mean Absolute Percentage Deviation）。 是一种衡量预测方法的预测准确性的指标。 MAPE 在解释相对误差（Relative Error） 方面非常直观，在评价模型时MAPE通常用作回归（Regression）问题的损失函数（Loss Function）。 从定义中可以看出，在计算MAPE时如果出现一系列特别小的分母，可能会出现一些问题。 比如分母为0 的奇异点、较小的误差引起结果发生非常大的变化等。 解决这个问题的替代方案是，可以将公式中的实际值，替换为该序列的所有实际值的平均值。 这种方案等效于求绝对差的总和除以实际值的总和，也被称为加权绝对百分比误差（WAPE），或者wMAPE（Weighted Mean Absolute Percentage Error）。 定义公式为：

（6） 对称平均绝对百分比误差SMAPE（Symmetric Mean Absolute Percentage Error）。 实际值与预测值差值的绝对值除以实际值与预测值绝对值之和的一半。 定义公式为：

2.2 实验模型介绍

本文采用BP 神经网络与LSTM 对于NPP数据进行预测。 模型统一输入48 天的数据作为历史信息，预测未来1 天的NPP值。 对于BP 神经网络，模型设计为输入层为48 个神经元；隐藏层为1 层，共计4 个神经元；输出层为1 个神经元。 BP 神经网络采用ReLU激活函数。 对于LSTM 网络，模型设计为48 个神经元；LSTM 层选择1 层，输出层采用48 到1的线性映射，并采用sigmoid激活函数。 LSTM 层中采用ReLU与tanh激活函数。

2.3 实验结果及分析

考虑到深度学习模型可以无限制地迭代，就会希望在即将过拟合时，或训练效果微乎其微时停止训练，因此研究采用早停（Early Stop）策略防止模型过拟合。 LSTM 和BP 神经网络损失函数如图3 所示。通过图3 可以看出，LSTM 神经网络模型和BP 神经网络模型的损失函数在迭代20 次后达到最小值。

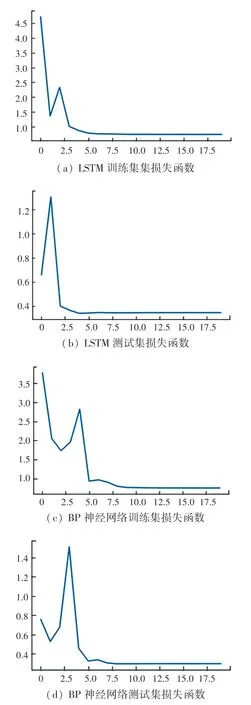
图3 LSTM 和BP 神经网络损失函数Fig. 3 Loss functions of LSTM and BP neural network

LSTM 和BP 神经网络在测试集上的预测值如图4 所示。 由图4 可以发现，BP、LSTM 等神经网络预测模型的预测结果与NPP的实际走向情况大体相符，误差也较小；而且很明显地，BP 神经网络的拟合能力更佳。 由图4 还会发现BP 神经网络预测模型的预测值与NPP实际数值最为符合的，而且预测值与NPP实际数值之间的偏差也很小。

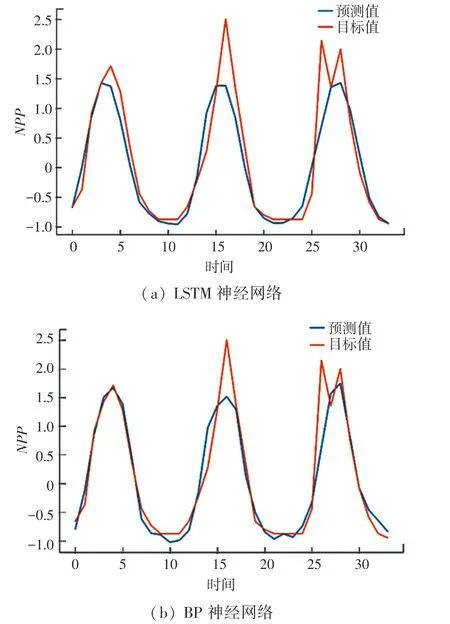
图4 LSTM 和BP 神经网络在测试集上的预测值Fig. 4 Predicted values of LSTM and BP neural networks on the test set

BP 神经网络和LSTM 神经网络评价指标结果值见表1。 由表1 可以看出，BP 神经网络模型所预测的SSE、MSE、RMSE、MAE、MAPE、SMAPE等的数据，显然都要比LSTM 的神经网络模型的小，大小依次836.058、24.59、4.958 83、2.755 98、0.218 6、0.152 19，说明了BP 神经网络的预测结果比较精确，并由此再次表明了BP 神经网络对该数据的检测结果，相比于LSTM 神经网络要更佳。

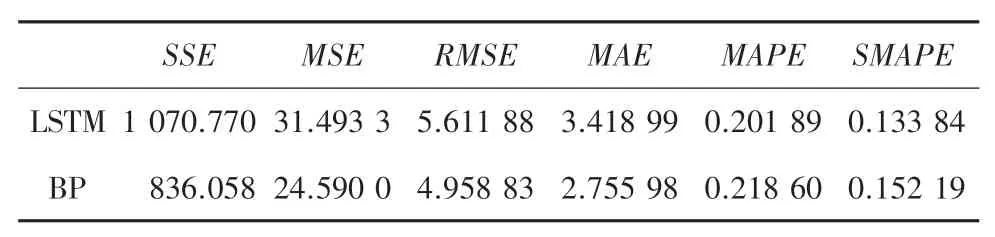
表1 BP 神经网络和LSTM 神经网络评价指标Tab. 1 Evaluation metrics of BP neural network and LSTM neural network

3 结束语

全球气候变化逐渐影响到生态系统的平和稳定，这一现象已日渐成为各学科进行学术研究的重要背景。 通过研究温度、降水、NDVI来预测兰州市NPP，能为全球气候变化及环境保护提供重要依据。 本文采用BP 算法和LSTM 算法，对NPP 进行预测。 通过对历史数据进行归一化处理后，再比较5 种数据的预期结果，从预测结果图的前5 种预测指标来看，BP 神经网络的预期结果相比于LSTM 神经网络更为出色，其SSE能够达到836 左右。 未来相关研究可以考虑将基于统计学的时间序列预测方法与深度学习方法相结合，从而更好地提取NPP 序列数据中的相关特征，并对其进行预测。