融合Savitzky－Golay 滤波器的TCN－SA－BiGRU 风电功率预测

秦小晖，樊重俊，付峻宇

（上海理工大学管理学院，上海 200093）

0 引 言

各国工业发展离不开资源消耗，也导致碳排放量数值上升，从而进一步引发温室效应、全球水平面上升等环境问题，所以随着技术的发展，风能、太阳能及潮汐能等清洁能源逐步取缔火力发电成为主要发电能源。 由于风能具有可再生性、无污染性等特点，所以目前风力发电仍是国内主要发电方式之一，但研究表明风能短时间变化随机，其发电功率呈间歇性以及波动性，所以使用风力发电会产生发电功率不稳定的现象，而这一现象也会导致电网运行风险提高，造成事故［1］。 因此准确预测风力发电功率能够提高风力发电的稳定性、减少不必要损失，从而提升经济效益。

随着预测技术的不断发展，国内外学者在研究过程中所使用的预测方法也从传统的统计模型预测逐渐演变成包含智能算法、机器学习以及深度学习的组合预测模型［2］。 早期的风电功率预测方法主要有：持续预测法、卡尔曼滤波法、灰色预测法以及随机时间序列法（例如AR、MA 以及ARIMA 等模型），但是存在预测时间范围小、数据收集及处理难度较大以及预测结果不稳定等问题［3］，所以后续也产生了改进相关时间序列模型以及将滤波器与时序模型组合的预测方法。

随着机器学习方法的面世，诸如支持向量机（SVM）、决策树以及随机森林等方法陆续涌现［4］，其中以支持向量机（SVM）的应用最为广泛，相较于传统的时序预测模型、马尔可夫等方法，SVM 在处理非线性等小样本时具有更好的适应能力，但是只采取SVM 单一模型进行预测的效果也并不好，所以在后续研究中，学者逐渐将SVM 与遗传算法相组合，利用算法对SVM 进行参数寻优以达到更好的预测效果［5］，例如粒子群算法、灰狼算法以及果蝇算法等等［6］，但这些算法多会存在收敛时间过长、出现局部最优解以及搜索步长设置繁复等问题，所以研究学者会对现有遗传算法进行优化后再对机器学习模型进行参数优化。

目前，主流的风电功率预测方法仍然是以神经网络模型为主的组合模型，在LSNet 神经网络、长短期记忆神经网络（LSTM）、门控循环神经网络（GRU）等基础上针对数据特征添加算法模型与之组合。 文献［7］经过研究发现GRU 网络相较于LSTM 网络在风电功率预测上的作用更加高效且结构简单。 而文献［8］建立融合注意力机制的Bi－GRU 模型对数据中所蕴含的信息进行深度挖掘，提高特征提取的效率与质量并进行预测。 文献［9］则利用TCN 神经网络与LSTM 神经网络进行组合对时序数据加以预测，TCN 网络可以较好地提取间隔较长和非连续时序数据的特征信息。

本文在已有研究的基础上，搭建融合Savitzky－Golay 滤波器的TCN－BiGRU 模型。 为了有效降低拥有噪声的风电功率数据，选取Savitzky－Golay 滤波器对风电功率相关特征数据进行降噪，并将预处理后的数据输入进TCN－SA－BiGRU 模型中，通过TCN 网络对相关数据进行特征提取，最后将有效信息输入进BiGRU 模型中进行预测。 本文选取西班牙某地区的风电功率数据以及其他历史相关数据以验证该组合模型的预测有效性。

1 模型原理介绍

1.1 时间卷积神经网络

时间卷积神经网络（Temporal Convolutional Network，TCN）最早于2016年由Lea 等学者提出，随后由Bai 等学者在文章中正式提出。 TCN 在卷积神经网络（CNN）的基础上做出改进，增加因果卷积以及空洞卷积。 TCN 中的因果卷积为单向结构，能保证提取信息特征时的因果性，即输入序列x1，x2，…，xt预测y1，y2，…，yt时，如果需要预测t时刻的值yt时只能利用已存在并观察到的x1，x2，…，xt－1，而不能使用xt＋1，xt＋2，…，所以TCN 中的因果卷积可以保证在时序预测过程中并不会受到未来信息因素的干扰，但是单纯的因果卷积受制于卷积内核大小，在抓取依赖信息特征时需要堆叠过多层数，所以TCN中又采用膨胀卷积增加网络中的感受野，对上一层输入信息增大采样范围以使得TCN 能够提取间隔较长以及非连续性数据的时序特征、即在更少层数的情况下能够抓取更多信息特征，同时TCN 在各网络层之间采用残差进行连接，防止梯度消失爆炸问题的产生［10］。 膨胀因果卷积结构如图1 所示，残差模块图如图2 所示。

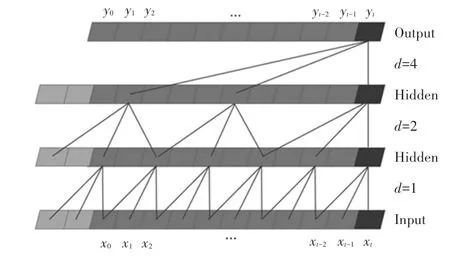
图1 膨胀因果卷积图Fig. 1 Structures of Causal and Dilated Convolutions

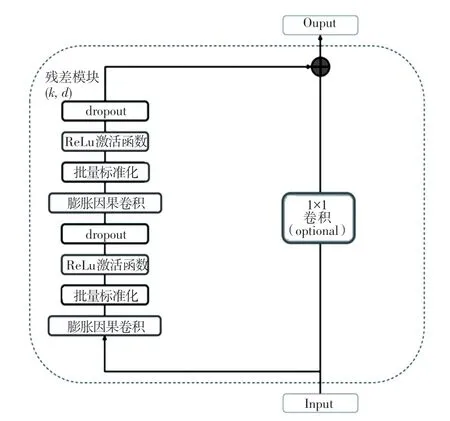
图2 残差模块图Fig. 2 Residual module

1.2 自注意力机制模块

由于在神经网络结构中所接收到的输入向量大小不一，同时这些向量之间所蕴含的信息可能存在一定关系，所以在模型训练中因为忽略了这些向量之间的关系而导致模型训练结果很差，而自注意力机制可以针对全连接神经网络中的相关输入变量较好地建立起数据相关性，从而提高了特征有效提取能力。 其公式如下：

其中，A为Attention，即注意力权重；Q为查询向量矩阵（Query Vector）；K为键向量矩阵（Key Vector）；V为值向量矩阵（Value Vector）。

1.3 双向门控循环单元

门控循环单元（Gated Recurrent Unit，GRU）是循环神经网络（RNN）的一种，由学者Cho 等学者在2014年提出。 GRU 与长短期记忆神经网络（LSTM）相类似，是在LSTM 基础上提出的衍生网络结构［11］，缓解了RNN 存在的梯度消失、且无法捕捉长期信息关联性等问题，并且GRU 的结构比LSTM 简单，具有计算效率高、网络参数较少等优点［12］。

GRU 结构如图3 所示。 由图3 可知，GRU 设置了2 个门。 其中，更新门zt用于控制t时刻的新旧输入信息保留程度；重置门rt用于控制t －1 时刻每个位置输入信息保留程度。 具体公式如下：

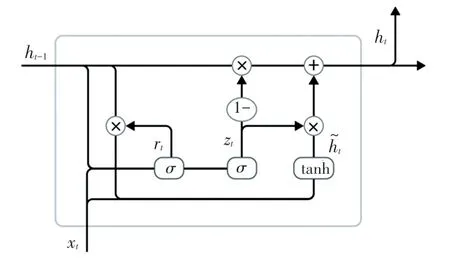
图3 GRU 结构图Fig. 3 Gated Recurrent Unit

其中，Wz、Wr与W分别表示更新门、重置门以及隐藏层的权重矩阵。

GRU 在进行预测时的顺序都是由前到后，这种单一方向的时序数据预测会导致具有长关联性数据的信息发生遗漏，所以在GRU 的基础上加入双向学习得到双向门控循环单元（Bi－GRU），其结构如图4所示。

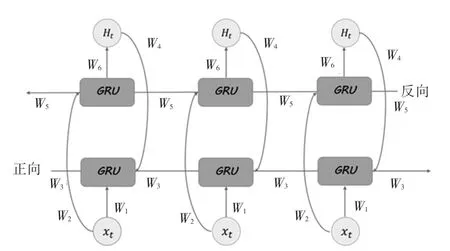
图4 Bi－GRU 结构图Fig. 4 Bidirectional Gated Recurrent Unit

由Bi－GRU 结构图可观察到，从正向来看，正向传导单元可以捕捉数据中的历史信息，从反向来看，反向传导单元可以捕捉数据中的未来信息，这种双向的结构可以实现全局信息捕捉，从而提高时序特征提取效率［13］。 更新后的公式如下：

其中，W为t时刻隐藏层状态；h为t时刻隐藏层权重；bt为t时刻隐藏层状态偏置。

2 融合Savitzky－Golay 滤波器的TCNSA－BiGRU 风电功率预测模型

2.1 Savitzky－Golay 滤波器

由于来自传感器的原始数据包含过多噪声会影响模型性能，所以很少被作为预测模型的输入数据。因此，在进行实验分析时，需要首先对数据进行降噪处理。 在本研究中，采用Savitzky－Golay 滤波器来去除原始数据的噪声。 Savitzky－Golay 滤波器由Savitzky 和Golay 在1964年提出，是一种基于时域局部多项式最小二乘拟合的滤波方法，常用于数据流平滑降噪。 作为一种有限脉冲响应（GIR）数字滤波器，通过卷积操作对原始时域信号进行平滑处理，而滤波后的数据在去除噪声的同时，保持了相同的信号结构。 作为光谱预处理中的常用方法，主要是对一定长度内的数据点进行k阶多项式拟合后得到拟合结果。

S－G 滤波是一种移动窗口的加权平均算法，但是其加权系数不是简单的常数窗口，而是通过在滑动窗口内对给定高阶多项式的最小二乘拟合得出，该算法的最大特点就是在滤除噪声的同时可以确保信号的形状、宽度不变。 公式如下：

其中，S表示原始信号；s∗表示降噪后的信号；Ci为第i次的降噪系数；N为（2m ＋1） 组数据的滑动窗口宽距；j为数据集中第j个样本。 当将滤波器应用于时间序列数据进行平滑处理时，必须确定滤波器中的2 个参数。 第一个参数N，是S－G 滤波器中的滑动窗口宽距，一般来说，当N越大时会产生更为平滑的结果，但同时会降低峰值的平整度；第二个参数k，表示S－G 滤波器中的拟合阶数，通常k值会设置在2 到4 的范围中。k值越小，会产生更平滑的结果，但可能会引入偏差；而k值越高，虽然会减少滤波器的偏差，但可能会发生过拟合现象，产生更大的噪声，所以调整N与k的大小是实现有效降噪以及信号平衡的关键所在。

2.2 S－G－TCN－SA－BiGRU 模型结构及预测步骤

本模型主要分为7 个模块：输入层、Savitzky－Golay 滤波器降噪层、数据拼接层、时域卷积层（TCN）、自注意力机制模块、双向门控循环单元以及输出层。 模型结构如图5 所示。 对模型中的各预测步骤将给出阐释分述如下。

图5 融合Savitzky－Golay 滤波器的TCN－SA－BiGRU 模型Fig. 5 TCN－SA－BiGRU model incorporating S－G filter

（1）数据输入。 对样本按照时间点位进行采样并进行数据预处理，将处理后的数据作为输入。 这里的数据包括风电功率数据以及相关特征数据（例如温度、湿度、大气压强、风速、风力等级、天气情况以及实际价格）。

（2）降噪。 假若全部数据进入S－G 滤波器进行降噪则会造成数据失真，所以选取部分数据进行降噪，根据样本设置S－G 滤波器中的滑动窗口宽距N以及拟合阶数k。

（3）数据拼接及划分。 将未降噪的数据以及降噪后的数据在此层进行拼接，并按照比例划分训练集以及测试集。

（4）模型训练。 将训练集输入进TCN－SABiGRU 网络中进行训练，首先利用TCN 时域卷积网络层对时序数据进行快速特征提取，再利用自注意力机制模块对特征进行权重调整，接着进入BiGRU网络中再次进行信息提取以更深层次地挖掘时序数据中蕴含的数据相关性，最后得到训练完成的TCNSA－BiGRU。

（5）预测及分析。 将测试集输入进已训练完成的TCN－SA－BiGRU 网络中进行风电功率预测，并设置对比分析实验以检测该组合模型的优越性。

3 实验

3.1 实验环境

实验所使用计算机配置见表1。

表1 实验环境Tab. 1 Experimental environment

3.2 数据选取

本实验数据来自Kaggle 数据网站上西班牙某地区2015年1月1日00：00 至2018年12月31日23：59 的风电功率数据。 每日共设24 个采样点，采样时间间隔为1 h，即每日数据集为24 维风电功率数据。 并且，陆上风力发电功率与一些其他的因素息息相关，所以本实验数据集包含了数据所属地的温度最大值及最小值、湿度、大气压强、风速、风力等级、天气情况以及电力实际价格。

3.3 数据预处理

3.3.1 数据缺失值处理

对数据进行缺失值处理，由于处理过程中未见大范围数据缺失、且数据采样间隔时间较短，故采取均值插补法对缺失数据进行填充。

3.3.2 数据标准化处理

由于在处理数据问题的时候，实验数据来自多个维度，例如本实验中温度、风力等因素会对风电功率产生影响，这一情况会产生以下问题：数据量纲不同导致数量级差别大；过大的数值会产生数值问题引发特征贡献度失衡。 所以为了避免以上问题，实验中选择对风电功率、温度以及压强等特征进行数据标准化处理，标准化公式如下：

其中，x′为重新调节后的数据向量，范围值为［0，1］，xmax与xmin分别表示数据集中的最大值与最小值。

对于离散型数据“天气质量状况”则进行Label Encoder 编码处理，例如：“晴天”为1，“雨雪天”为2，等等。

3.4 实验评价指标

本文模型评价指标选取决定系数（coefficient of determination，R2）、 平均绝对误差（mean absolute error，MAE） 以及均方误差（Mean Square Error，MSE）。

（1）决定系数（R2）。 一般用来表示模型预测拟合程度。 计算公式如下：

（2）平均绝对误差（MAE）。 用来准确反映实际预测误差的大小。 计算公式如下：

（3）均方误差（MSE）。 用来衡量观测值同真值之间的偏差。 计算公式如下：

其中，yi表示原始数据；表示拟合数据；表示原始数据均值。

决定系数R2取值范围为［0，1］，R2取值越接近1 表示拟合效果越好，平均绝对误差MAE以及均方根误差MSE的取值则越小越好。

3.5 实验结果及分析

利用S－G 滤波器对部分风电功率及相关数据进行降噪处理，由于滤波器中的参数无法对数据进行自适应处理，故在多次对比实验后设置S－G 滤波器中滑动窗口宽度N为59，拟合阶数k为3。 此后在拼接层将降噪完的数据与原输入未降噪后的数据进行拼接输入进TCN－BiGRU 网络中，设置模型训练迭代次数为100 次，TCN 网络中的膨胀系数设置为以2 的倍数进行叠加，BiGRU 网络中神经单元数为64，其中BiGRU 网络层数为1 层。

为了更直观地展示该组合模型的预测精度，故设置对比实验以及消融实验。

3.5.1 对比实验

为了验证模型预测性能，该处选择传统循环神经网络（RNN）、长短期记忆神经网络（LSTM）以及双向循环门控单元神经网络（BiGRU）进行对比，各模型预测值与真实值对比结果见表2。

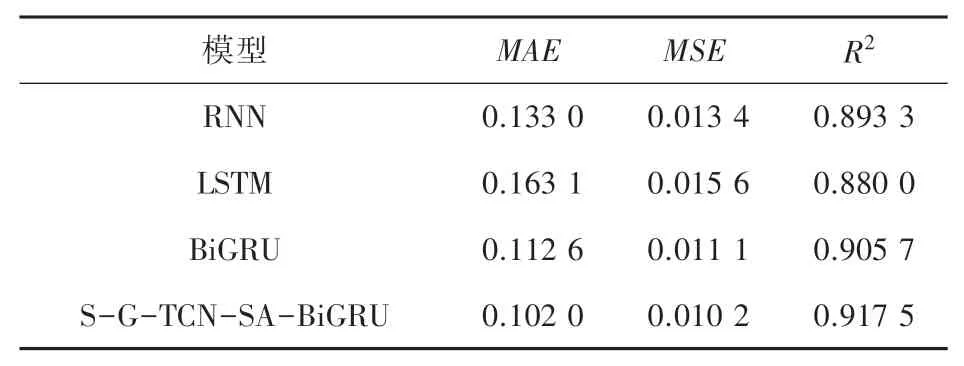
表2 对比实验结果Tab. 2 Comparison of experimental results

由表2 中结果可以看出，融合Savitzky－Golay 滤波器的TCN－BiGRU 模型的预测值以及预测性能要比上述所提到的对比模型都具有优势。 与传统循环神经网络（RNN）相比，本组合模型的MAE降低了0.031，MSE降低了0.003 2；与长短期记忆神经网络（LSTM）相比，本组合模型的MAE降低了0.061 1，MSE降低了0.005 4；同双向循环门控单元神经网络（BiGRU）相比，本组合模型的MAE降低了0.010 6，MSE降低了0.000 9；从拟合程度来看，本模型的拟合程度最高。 综上可以表明，本组合模型在风电功率预测方面的结果是更为精确的。

3.5.2 消融实验

为了验证本文组合模型中各个模块的合理性，研究设置了消融实验：剔除TCN 时域卷积神经网络、剔除自注意力机制模块以及剔除S－G 滤波器，实验结果如图6 所示，实验指标对比见表3。

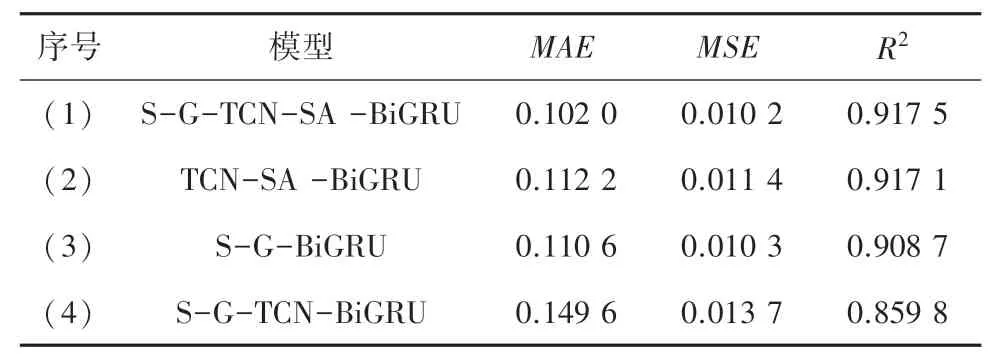
表3 消融实验对比结果Tab. 3 Comparative results of ablation experiments

图6 消融实验预测值对比Fig. 6 Comparison of predicted values for ablation experiments

从图6 以及表3 中的结果可以看出，模型（2）的MAE相较于模型（1）高了0.010 2，MSE高了0.003 5；模型（3）的MAE相较于模型（1）高了0.008 6，MSE高了0.000 1；模型（4）的MAE相较于模型（1）高了0.047 6，MSE高了0.003 5；。 综上，在分别剔除S－G滤波器、自我注意力机制模块以及TCN 时域卷积网络结构后，每一种模型的MAE以及MSE都有所上升，这也证明了本文所提出的组合模型的每个结构在模型预测性能方面都有一定的提升作用，进而表明组合模型的预测性能要优于单个模型。

4 结束语

（1）本文所使用的Savitzky－Golay 滤波器在一定程度上对数据进行了有效降噪并提升了预测模型整体的预测精度，但该滤波器中的参数需要根据输入数据进行调节，所以在此研究基础上可进一步利用算法优化S－G 滤波器的滑动窗口参数N以及拟合阶数k，用来提高模型对于不同数据的适应性。

（2）在风电功率预测方面，“融合Savitzky－Golay 滤波器的TCN－SA－BiGRU 模型的风电功率预测性能更高”这一实验目的在经过对比、消融实验后得到验证，模型结构中的TCN、自我注意力机制模块以及双向学习策略结构不仅提升了预测性能，并且其提取数据特征速度更快，能够更好地挖掘时序数据中所蕴含的信息要素。

（3）基于本模型的研究更多方面是展现模型的优化，而针对风电功率预测等实际应用场景应当进一步寻找合适的预测模型进行研究。