基于改进蚁群算法的农村运输路径规划

黄二强，代永强，刘 欢

（甘肃农业大学信息科学技术学院，兰州 730000）

0 引 言

随着国家对环境保护的重视，农业得到了飞速发展，农产品的产量也有了全面提升，需要良好的交通运输路径来激活农村经济。 因为国内地形地貌复杂多样，各地的农村之间相距较远、且农产品种类和产量也不相同，所以就需要规划运输路径的软件，来帮助规划路径，车辆运输路线规划已经变得越来越重要。 相对于常规的路径规划算法，首先，本文中的算法弥补了在运输的整个环节中花费在农村收购点等待农产品的时间，因为地理原因，收购商到达农村收购点后，因为不同地区的果园或农田距生活区较远，有的地势陡峭、有的地质松散、比较危险，农民也会在不同的时间去采摘农产品，造成收购商额外花费的时间不同。 而常规的路径规划算法中只注重车辆调度花费的时间。 其次，本文中改进的蚁群算法融合退火算法后，提高了蚁群算法跳出局部最优的能力和收敛速度。 再次，通过融合蜜獾算法，在计算2 个收购点之间的距离时，本文考虑到农村地形影响因素，引入蜜獾算法在挖掘阶段的心形模型来计算两点间的距离，此模型更适合计算农村收购点之间的距离，其距离与实际路程更接近。 而常规算法是计算连点间直线距离，在计算山区中2 个农村之间的距离时，计算的直线距离与实际路程比本文中的要差。 本文选择甘肃省若干个村镇进行路径规划，利用改进的蚁群算法帮助收购商寻找一条最佳的运输路径。 运输路径规划问题可归于TSP［1］（traveling salesman problem）问题，在解决TSP 问题上，可用精确算法［2］或启发式搜索算法［3］，如分层递进的改进聚类蚁群算法［4］或者人工智能算法，如模拟退火算法［5］、蚁群算法［6］、禁忌搜索算法［7］、鸡群算法［8］、粒子群算法［9］、蜂群算法［10］、麻雀搜索算法［11］以及遗传算法［12］等。 在本文中用改进的蚁群算法来规划车辆运输路径。 基于原始蚁群算法中跳出局部最优的能力低［13］、收敛速度慢［14］、优化效率低［15］的问题，改进的算法中，首先增加蚂蚁体重突变的因素，可以提高蚁群的多样性，从而提高蚁群算法跳出局部最优的能力。 在蚂蚁体重突变的过程中，通过结合退火算法的概率计算方法来得到当前运动蚂蚁的体重；其次，增加目标地点的时间权重参数，可通过设置目标点的时间权重值更快、更准确地找出下一个地点，提高了蚁群算法的收敛速度。 实验结果表明，改进的蚁群算法有更好的寻优能力。

1 蚁群算法

蚁群算法是Dorigo 等学者［16］在二十世纪九十年代提出的一种新型的模拟进化算法［17］。 通过研究发现蚂蚁之间传递信息是通过一种称为信息素的物质，当蚂蚁在寻找食物时通过这种物质进行信息交互的。 蚂蚁在觅食的过程中会在经过的路径上留下信息素，并且蚂蚁也能够感受到信息素，蚂蚁会通过判断信息素来指导自己运动的方向：若无信息素则按照随机性前进，若有信息素、则根据信息素的强度来确定自己的运动方向。 蚂蚁会选择信息素、浓度高的方向运动。 由于大量蚂蚁组成的蚁群集体行为表现出一种信息正反馈现象，在某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大。蚁群算法相对于其他的一些算法很有优势，文献［18］中利用Matlab 对蚁群算法和遗传算法对TSP的求解进行了研究对比，研究发现，在若干个城市里，无论两地之间距离多远，蚁群算法比遗传算法更优。 在文献［19］ 中设计了一种包含改进PRM（probabilistic road map）算法和蚁群算法的一种融合算法，可以一次规划出多个目标点的路径，但是所规划出来的路径具有随机性。 文献［20］中将蚁群算法和粒子群算法对比，蚁群算法的可靠性和精确度高、适应性强。在该算法中，将m只蚂蚁随机性地放在了n个城市里，全部的路径（i，j） 上信息素的初始值△τij（0）＝常数（C），之后蚂蚁k（1，…，m）在t时刻就按照其转移概率来选择出下一个节点。

2 模拟退火算法

模拟退火算法（Simulated Annealing，SA）最早的思想是由N. Metropolis 等学者［21］于1953年提出［21］。 1983年，Kirkpatrick［22］成功地将退火思想引入到组合优化［23］领域。 这是基于Monte－Carlo［24］迭代求解策略的一种随机寻优算法［25］。 王光等学者［26］提出的算法进行可靠性模型参数求解，具有解的全局性好、收敛速度快等优点。 其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。 本质思想为以概率接受新状态：在温度为T时，设当前状态为i，新状态为j，若Ej ＜Ei，则接受j为当前状态；否则，若概率大于［0，1） 区间的随机数，则仍接受状态j为当前状态；若不成立，则保留状态i为当前状态。p ＝：在高温下，可接受与当前状态能量差较大的新状态；在低温下，只接受与当前状态能量差较小的新状态。 该式中的K为玻尔兹曼常量，是热力学的一个基本常量，数值为1.380 649×10－23J／K。

3 蜜獾算法

蜜獾算法（Honey Bavdger Algorithm，HBA）是2022年提出的一种元启发式优化算法。 该算法的灵感来源于蜜獾的觅食行为，蜜獾会通过挖掘阶段和采蜜阶段寻找食物，还会根据气味强弱接近猎物捕食。 该算法具有开发能力强、收敛速度快等特点，但探索能力有所不足。 研究发现，蜜獾算法的挖掘阶段的心形模型类似于农村收购点之间的路线形状，故而将蜜獾算法融合到农村收购点路径优化算法中。

4 改进的蚁群算法

针对蚁群算法收敛速度慢的问题，先提出对原始蚁群算法［27］的信息素优化方法，其次讨论了改进的蚁群算法的原理。

4.1 信息素的优化

首先，在改进的蚁群算法中对参数信息素重要程度α和信息素启发式因子β进行多次实验得到的最优值并将其参数值都设置为最优值2。 其次，根据蚁群生物学［28］了解到蚁群中由工蚁、兵蚁、雄蚁、蚁后等组成，其中在工蚁或兵蚁或雄蚁中的蚂蚁的个体大小和体重并不一样，而其中更重的蚂蚁对信息素时的释放量比更轻的蚂蚁释放得更多，由此引入蚂蚁的体重突变因素不仅增加了蚁群的多样性，而且间接地影响了蚂蚁释放信息素的量；在原始蚁群算法中，信息素的释放量是一个常量，而在改进的蚁群算法中将其信息素改为可变的量。当一只蚂蚁从i点到j点，若从i点到j点的路径不是最优路径时，由于越来越多的蚂蚁的移动将由信息素来进行导向，那么从（i，j） 路径上走过的蚂蚁就越来越多，导致蚁群算法跳出局部最优的能力越差。 根据下文函数（8）可以看出，可以通过蒙特卡洛准则中的概率公式得到蚂蚁体重突变概率F，进而可以得到该蚂蚁的体重，因为下一个农村点的时间权重值越大，则该地点需要等待的时间越长，而两地时间权重值的差值越大，则函数（8）得到的概率值F就越小，再通过下文函数（5）可以看出，F越小、则蚂蚁体重突变的概率越小，进而该蚂蚁释放的信息素就越少，反之则释放的信息素越多，最终提高了蚁群算法跳出局部最优的能力，加快了算法的收敛速度。

4.2 算法介绍

将m只蚂蚁随机性地放在了n个城市里，路径（i，j） 上信息素的初始值τij（0）＝0，蚂蚁k（1…48）在t时刻按照其转移概率来选择出下一个节点。 通过多次实验测试得出，信息素重要性α的值和启发式因子β的值分别设置为2和2，将蚂蚁的体重突变作为影响启发式因子的因素，蚂蚁的体重越大，且当前路径的距离越短，启发信息越大，则选择此路径的可能性越大；实验测试得出，改进蚁群算法的收敛速度更快、得到的解更优。 由此推得的公式为：

其中，Lij表示通过蜜獾算法的挖掘模式计算得到农村山区路段（i，g，j）的距离，s表示蚂蚁通过体重突变后的体重。 函数（2） 中考虑到山区地形因素，引入了车辆体重因素对道路顺畅度的影响：车体越重的、主要考虑路线长短的因素，次要考虑时间长短的因素。

各个路径所含的信息素更新公式为：

其中，1－ ρ表示信息素残留因子，ρ∈（0，1）。

其中，△τij表示在本次所有蚂蚁运动到目的地时，路径（i，j） 上蚂蚁的信息素总量； 在初始时刻△τij（0）＝0，指的是第k只蚂蚁在此次循环时留在路径（i，j） 上的信息素总量。 此处需用到如下公式：

首先，从函数（5）中可以看出在信息素释放量的影响因素中添加了车辆重量因素，其车重超出标准越多、且路程越长时，路段（i，j） 上释放的信息素就越少，选中该路段的概率就越小，反之则概率越大。 其次，是通过蜜獾算法中挖掘阶段的心形模型计算两点之间的路程，通过该模型得到的路程更符合实际情况：

在实际情况中考察得知，农村收购点之间需要翻过山丘或者大山，其路程是弧形的、与蜜獾算法的挖掘阶段的心形模型类似，在蚂蚁搜寻的初始阶段按照蜜獾算法中的挖掘阶段的模型找到一个随机产生的坐标（xg，yg，），可以通过该模型计算2 个农村收购点（i，j） 之间的实际距离为（i，g，j），算法如下：

其中，xg为模型在经度上的弧度；yg为模型在纬度上的弧度；α、r0、r1、r2为（0，1）的随机数。

在此基础上，又推得数学模型公式具体如下：

5 模型构建及求解

5.1 选取48 个农村点

在甘肃省内选择48 个农村种植区的经纬度作为坐标，通过改进的蚁群算法进行路径规划。 选取的农村种植区的坐标见表1。

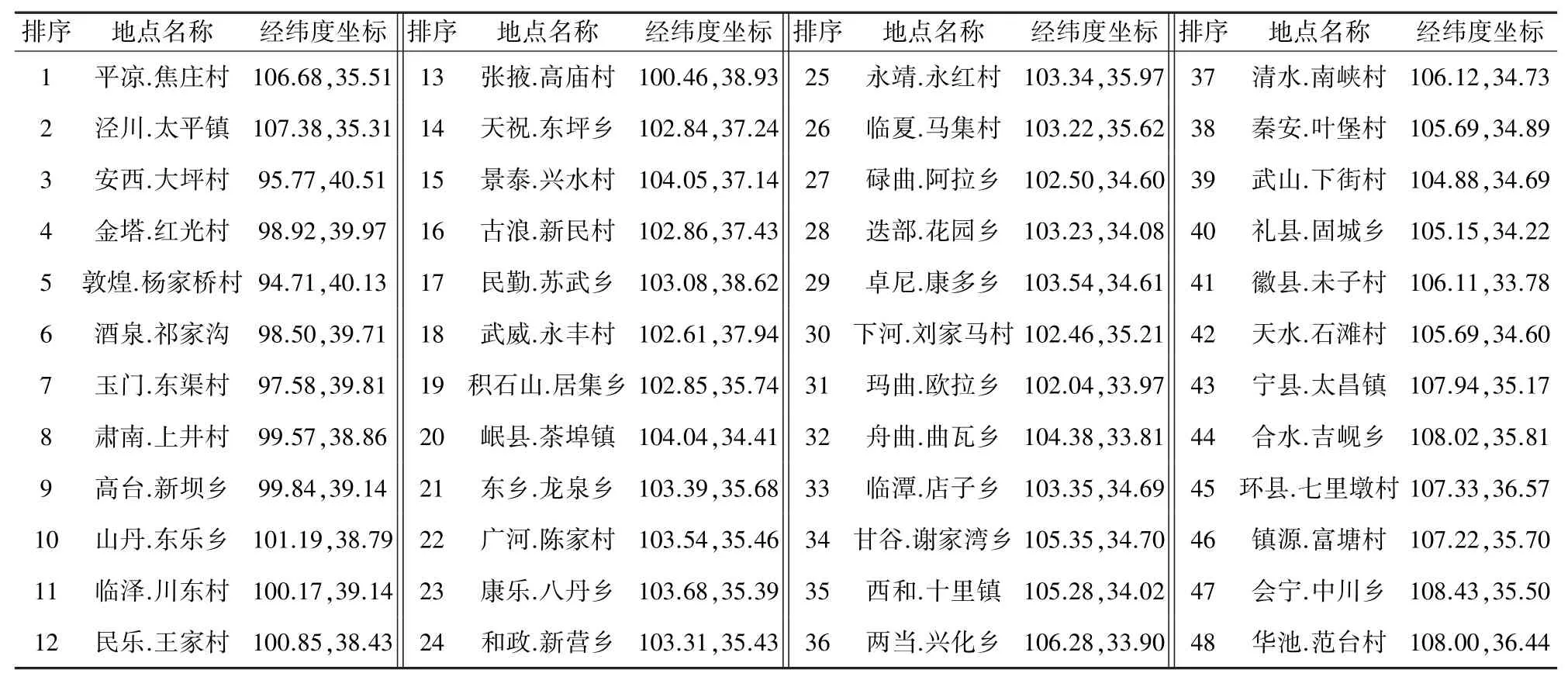
表1 农村坐标表Tab. 1 Rural coordinates

5.2 问题分析

商贸企业在经营过程中以效益为首，需要开源节流，而运输过程中消耗的时间和资源是商贸企业支出的重要的一部分，通过对商贸企业运输车辆的路径规划可以让商贸企业减少开支。 商贸企业在采购农产品时，首先，为了减少不必要的车程开销，假设运输车辆从一个农村点出发、从所有农村点只经过一次。 直至到达最后一个农村点的前提下，规划出路程最短的最优路径，类似旅行商问题。 本文利用改进的蚁群算法求解运输路线的最优路径。 其次，以收购农产品为例，计算所需天数。 不妨假设从平凉.焦庄村出发，经过所有农村点、直到最后一个农村点，花费的时间包括运输车辆在路上的时间和在农村点等待收购所花费的时间；根据前面求解出的最佳运输路径，计算出所需的天数，并且对运输过程做具体的安排。

5.3 求解实例与仿真

改进的蚁群算法给参数设定的值可以应用到农产品运输路径规划中，首先在时间权重T ＝1 时对运输路线进行规划，其次时间权重T的值分别按3种方案对运输路线进行规划。 通过实验得到各地点在3 种时间权重情况下的运输路径规划结果。

5.3.1 算法对比

首先，绘制出48 个农村点的坐标，如图1 所示。其次，当时间权重值T ＝1 时，求出原始蚁群算法和改进的蚁群算法在200 次测试中每一次得到的最优路径长度，如图2 所示。 最后，通过对表2 中的2 种算法在最优解、平均解和耗时三方面做对比，可以看出改进的蚁群算法收敛速度更快、跳出局部最优的能力更强、得到的解更优，并绘制出改进的蚁群算法求解得到的最优路径图，并进行2 种不同的展示，如图3、图4 所示。

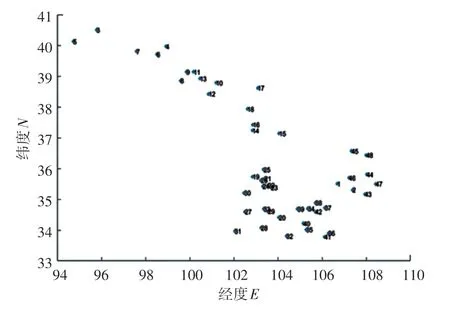
图1 48 个地点分布图Fig. 1 Distribution of 48 sites

图2 各地时间权值T ＝1 时的路径曲线图Fig. 2 Path curve when time weight T ＝1

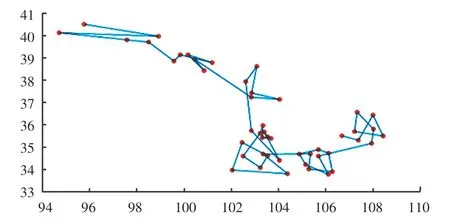
图3 无经纬度的最优路径Fig. 3 Optimal path without longitude and latitude

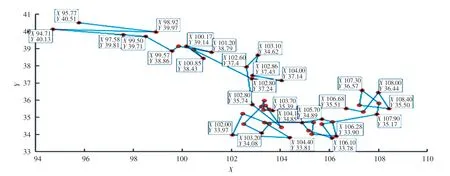
图4 有经纬度的最优路径Fig. 4 Optimal path with longitude and latitude

表2 算法比较Tab. 2 Comparison of algorithms

5.3.2 设置时间权重表

从往年的收购花费时间的记录中可以预估两地之间从出发到完成农产品收购需要花费的天数、即时间权重，在3 种不同的天气给48 个农村点设置时间权重值T；T ＝1 指的是运输车辆到达农村时、可以立即开始收购农产品，值为1.5、表示需要等待0.5天才可以收购农产品，其余值依此类推。

5.3.3 求最优路径

在改进的蚁群算法中，根据表3～表5 三个方案的时间权重值分别求出对应的最优路线。 经过200 次测试，得到运输车辆的3 种最优路径，如图5～图7 所示。3 种策略得到的曲线如图8 所示。 根据图8，可以看出3 条路线的收敛速度、及最优路径的路径总长。 车辆央最优路径上花费的时间的结果曲线如图9 所示。 根据图9，可以看出每辆车经过全程所花费的时间。

图5 根据表2 得到的最优路径Fig. 5 The optimal path obtained according to Table2

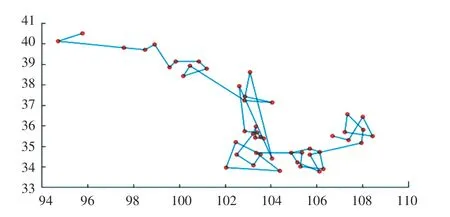
图6 根据表3 得到的最优路径Fig. 6 The optimal path obtained according to Table3

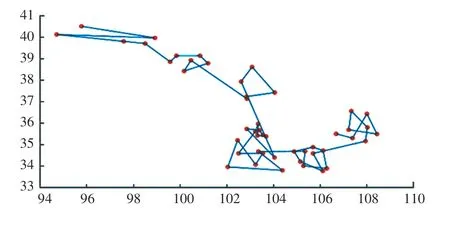
图7 根据表4 得到的最优路径Fig. 7 The optimal path obtained according to Table4

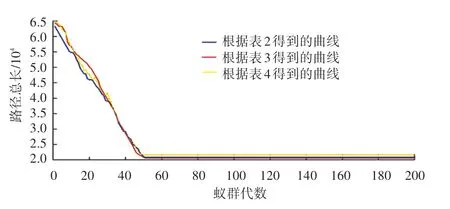
图8 3 种策略得到的曲线Fig. 8 Curves obtained by three strategies

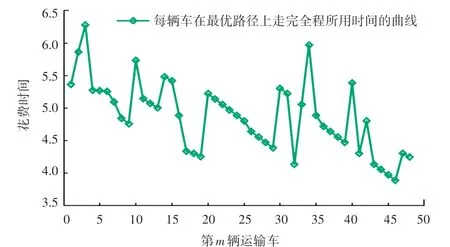
图9 车辆在最优路径上花费时间的曲线Fig. 9 Curve of time spent by vehicles on the optimal path

表3 方案一的各地的时间权重值Tab. 3 Time weight value of each region in scheme I

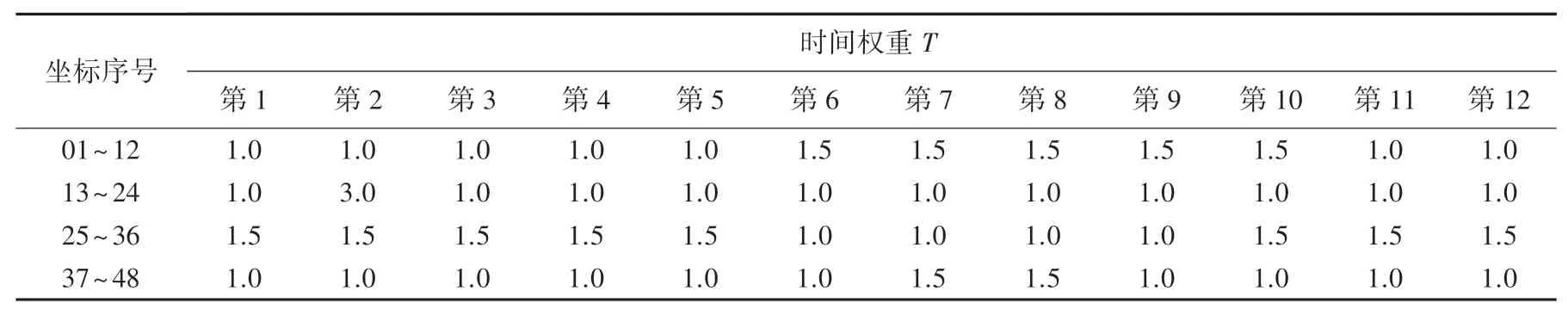
表4 方案二的各地的时间权重值Tab. 4 Time weight values of different regions in scheme II

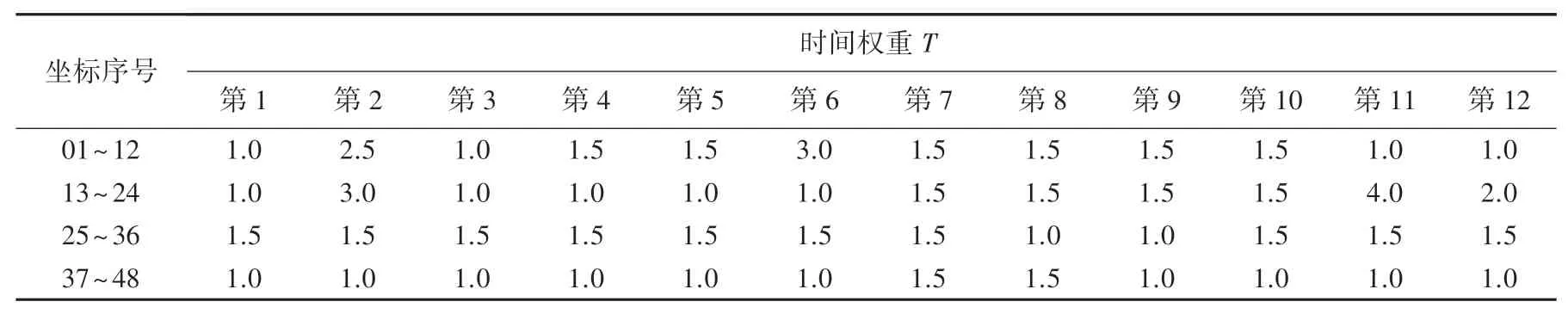
表5 方案三的各地的时间权重值Tab. 5 Time weight values of different regions in scheme III

5.3.4 规划路径的建议

从图5～图8 看出，可以通过设置时间权重来规划出路径方案，该方案可以在花费最少的时间、农产品价格最低、成熟度最好时，到达各农村收购和运输农产品，通过这种方法可以消耗最少的资源来得到最大的收益。 从图8 中可以看出红色曲线的运输规划路径在地理顺序和路程总长两方面是最优的运输路径。 经过这48 个农村的最佳运输路路径为：2—1—3—4—5—6—7—10—8—9—11—15—13—14—12—16—18—17—21—20—19—22—23—26—25—27—28—30—29—33—36—30—31—32—34—35—39—37—47—42—44—38—45—48—46—43—41—40。 花费总时间：3.888 9 天，实际上就是需4 天。

行程安排：要完成这些村镇的农产品的收购工作，总共需要4 天。 如果企业安排收购任务的时间比较宽裕，可以在符合时间范围内的规划路径中将天气等因素考虑其中，如此就可以更完美地规划运输路径了。

6 结束语

本文提出了一种改进的蚁群算法，并将其应用到农村运输路径的优化求解。 首先，在基本蚁群算法中引入了模拟退火算法的随机概率作为蚂蚁体重突变的策略的参数和时间权重参数，使算法更快地跳出局部最优；采用蚂蚁体重突变策略增强了种群的多样性，提高了全局搜索能力和算法的收敛速度。 其次，根据农村运输的环境建立模型，并建立目标函数。 最后，通过Matlab 进行仿真实验，结果表明优化蚁群算法能够更快速地找出最优路径以及在运输过程中花费的时间，有效提高了运输路径规划的效率。 运输路径规划受环境的影响较大，本文开展的研究未考虑天气、高山等环境因素的影响，在以后的研究工作中将增加其他影响运输路径规划因素进行系统研究。