海上风机变径单桩基础竖向承载特性及变径参数影响研究
2023-02-28朱洪泽
郑 川,朱洪泽,王 皓,苏 凯,3,4
(1.浙江华东工程咨询有限公司,浙江 杭州 310014;2.武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072;3.武汉大学水工岩石力学教育部重点实验室,湖北 武汉 430072;4.武汉大学海绵城市建设水系统湖北省重点实验室,湖北 武汉 430072)
0 引 言
随着我国推行新能源建设力度的加大,风能受到了越来越多的关注。得益于我国绵长的海岸线,近几年我国海上风电得到了快速发展[1]。在海上风机建设过程中,基础是海上风机总体成本的决定性因素,其安装成本占总成本的15%~30%[2],因此选择合理的基础结构型式成为发展海上风电的核心技术之一。单桩基础结构简单、安装方便,是一种应用广泛的基础型式,在全球海上风电中占比约为80%。随着海上风机装机量增大,对桩基的竖向承载性能提出了更高的要求,常规的通长单桩基础难以同时满足施工与结构安全的要求,而变径单桩基础既可以满足连接性要求,还可以提高结构承载力,因此得到越来越多的关注与应用[3]。
目前对于桩基竖向承载力的确定方法主要有理论计算、试验分析、数值模拟等方法,其中现场静载试验是最为认可的方法,但静载试验花费较高,时间周期较长,在大直径长单桩中很少采用[4,5]。数值模拟方法能够快速利用工程数据进行相关分析,大量研究成果表明数值模拟与试验结果吻合度较高,是一种进行单桩承载性能计算的有效方法[6-10]。然而,现有的研究成果大多是针对通长单桩基础,尚未对大直径超长变径单桩基础的竖向承载能力进行深入研究。
鉴于此,本文利用有限元分析软件ABAQUS 建立置于复杂多层土体环境下的变径桩模型,对比变径桩与通长桩承载特性的差异,研究变径桩不同尺寸参数对桩基竖向承载特性的影响,以期为海上风电变径单桩基础的设计提供参考。
1 工程背景及有限元模型建立
1.1 工程背景
本文计算参考江苏某海上风电场工程,工程总装机规模为800 MW,统一采用单桩基础形式。风电场位于黄海海域,地质勘测得到风电场地基土物理力学性质详见表1,根据贯入试验结果确定其中地基持力层为⑤-1。
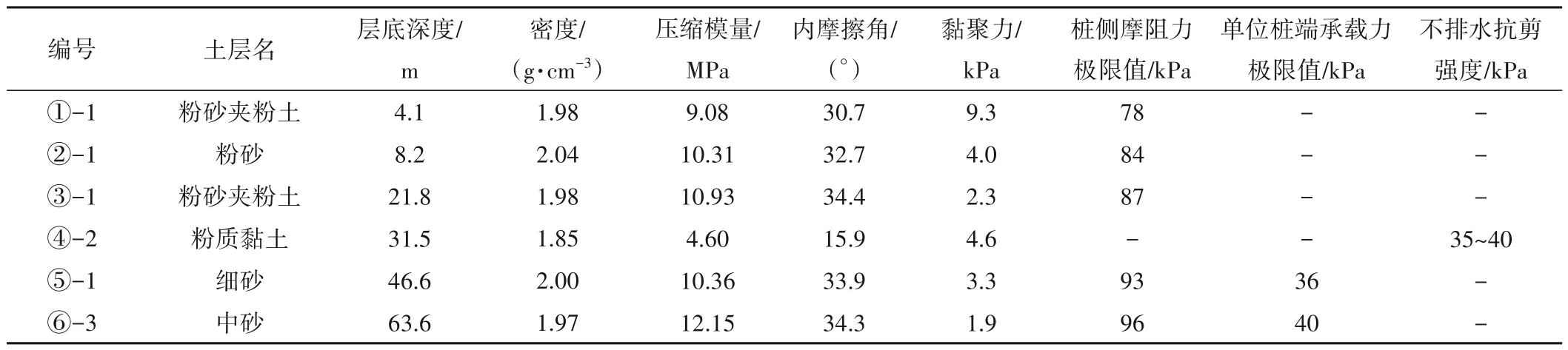
表1 土层物理力学参数表Tab.1 Physical and mechanical parameters of soil layer
1.2 结构尺寸及有限元模型
以此风电场中85号机位风机变径单桩基础结构为例,其示意图如图1(a)所示。其中,DT、DB分别表示桩顶和桩底直径;H1、H2和H分别表示单桩上部长度、变径段长度以及桩基总长度。该变径单桩基础的桩顶直径DT=6.0 m,桩底直径DB=6.5 m,上部高度H1=22 m,变径段长度H2=15 m,总桩长H=84 m,桩基埋深55 m,壁厚70 mm。
利用ABAQUS 建立如图1(b)所示的变径单桩基础三维有限元模型。土体径向模型取20倍单桩底部直径长度[11],土层计算厚度取1.25倍基础埋深[12],以避免边界效应。桩基础和土体均采用C3D8R单元,其中桩基础网格的竖向尺寸为1 m,土体网格密度沿径向变化,靠近桩基础处的网格径向尺寸为0.75 m。

图1 变径桩基础模型示意图Fig.1 Schematic diagram of variable diameter monopile foundation model
1.3 模型设置与材料参数
土体模型底部施加全约束,侧面施加径向约束,顶部为自由面。材料参数方面,土体采用Mohr-Coulomb 模型,单桩假定为线弹性材料。单桩材料为Q355 钢材,密度为7 850 kg∕m3,弹性模量为206 GPa,泊松比为0.3。通过定义面面接触模拟桩-土间相互作用,设置桩体为主面,土体为从面,切向采用Coulomb 摩擦模型,法向采用硬接触,摩擦系数取μ=tan(0.75φ),其中φ为土体内摩擦角[13]。单桩顶部设有耦合点,用于施加位移约束或者竖向荷载,输出耦合点反力即可得到桩顶荷载-沉降曲线。荷载步设置方面,首先进行地应力平衡计算,再激活单桩基础以模拟工程实际施工情况。
2 变径桩竖向承载特性
考虑到变径段的存在,变径桩在承受竖向荷载时,桩身对土体的作用会与通长桩基础有所不同。为对比两者的竖向承载特性,本研究还建立顶部直径与变径桩相同的通长桩模型,并对两者梯级施加竖直向下的相同幅值荷载。
计算得到轴力分布如图2所示,其中轴力方向根据坐标系确定。由图2可知,沿深度方向桩身轴力不断减小,但桩底处的轴力并不为0,说明桩端土体也承担了部分竖向荷载。同时,变径桩与通长桩桩身轴力分布基本一致,说明当前模型条件下,变径段对轴力分布的影响基本可以忽略不计。
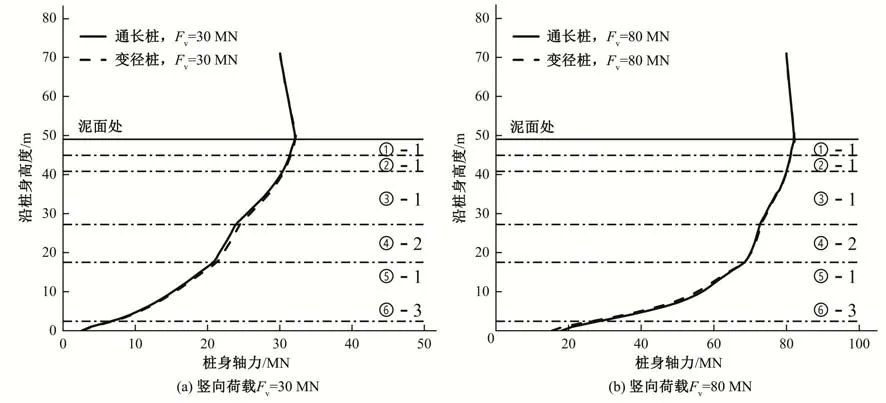
图2 变径桩与通长桩桩身轴力分布对比图Fig.2 Comparison of axial force distribution between variable diameter monopile and the pile with the same diameter
进一步,为分析单桩竖向承载力的构成,提取桩身内外侧摩阻力(沿桩身向上为正)分布如图3所示。由图3可知,随着竖向荷载增大,桩身两侧摩阻力均逐渐增大。由于土体压力分布以及桩体相对滑动的作用,单桩外侧摩阻力在距桩底约2 m处达到最大值,随后快速衰减;而由于桩内土体会发生压缩变形,产生相对于管壁向上的位移,因此单桩内侧摩阻力主要出现在桩段下部分,桩身上部内侧摩阻力值较小,可忽略不计。

图3 变径桩与通长桩侧摩阻力分布对比图Fig.3 Comparison of side friction resistance distribution between variable diameter monopile and the pile with the same diameter
在前文基础上,计算桩身内外侧摩阻力及桩端阻力承载比如图4所示。当竖向荷载小于40 MN 时,此时两类桩基均未达到竖向极限承载状态,各分量的承载值与施加的竖向荷载基本呈线性关系,但占比保持不变。随竖向荷载增大,内侧摩阻力与桩端阻力的承担荷载占比快速上升,而外侧摩阻力则明显降低。同时,相较于通长桩基础,变径桩外侧摩阻力占比更高,相对应的桩端阻力占比则低于通长桩基础。

图4 变径桩与通长桩承担荷载分量变化对比Fig.4 Comparison of the variation of the component of the bearing load between variable diameter monopile and the pile with the same diameter
采用位移控制方式,对桩顶分级施加位移荷载使桩身竖向沉降达到0.5 m,得到两类桩基荷载-沉降关系曲线如图5所示。可以看出,桩基的荷载-沉降曲线存在明显的拐点与陡降段,因此可确定该转折点处荷载值为桩基竖向极限承载力[14]。由此得到通长桩竖向极限承载力为42.7 MN,变径桩竖向极限承载力为48.5 MN,较前者增加约16%。主要原因在于,采用变径桩基础时,桩基与土体的接触面积增加使得桩侧摩阻力提升,从而提高了单桩基础的竖向极限承载力。

图5 变径桩与通长桩荷载-沉降曲线对比Fig.5 Comparison of load-displacement curves between variable diameter monopile and the pile with the same diameter
3 变径桩特性影响
在前一节基础上,考虑到变径桩的尺寸参数可能会影响其竖向承载力,本节将从变径桩底部桩径DB、变径段上部长度H1、变径段长度H23个方面展开分析。
3.1 变径桩底部桩径影响
考虑变径桩底部桩径变化范围为6.0~9.0 m,并保持其他参数不改变。对桩基础施加0~0.5 m 竖向位移荷载,得到不同方案沉降-位移曲线如图6所示。从中可以看出随着底部桩径的增大,使桩基沉降到同一位移所需的荷载值增大。对比6.0 m底部桩径基础,当底部桩径增大到9.0 m 时,桩基竖向极限承载力增加量约为27.4 MN,增幅约为71%;同时,各方案竖向极限承载力变化规律表明二者基本呈线性正比关系。

图6 变径桩底部桩径影响Fig.6 Influence of pile diameter at bottom of variable diameter monopile
在桩基顶部施加30 MN 的竖向荷载,得到部分方案桩身轴力分布如图7(a)所示。由图7(a)可知,随着底部桩径增大,轴力衰减速度逐渐增大,这主要是由于桩土接触面积增大,使桩侧摩阻力增大,从而使桩身轴力衰减速度增大。提取不同承载分量与桩径变化间关系曲线如图7(b)所示。从图7中可知,随着底部桩径增大,外侧摩阻力逐渐增大,但增量逐渐减小,内侧摩阻力与桩端阻力则随底部桩径增大而减小,并趋于稳定。
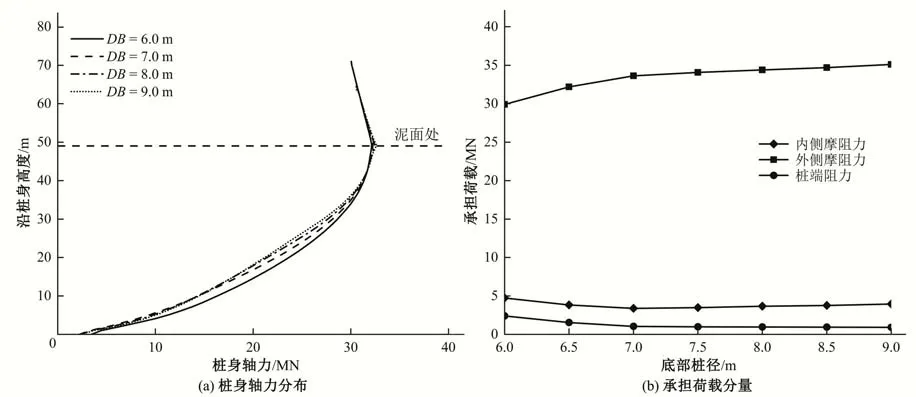
图7 不同变径桩底部桩径条件下桩身轴力分布及承载分量变化Fig.7 Axial force distribution and the variation of the component of the bearing load under different pile diameters at bottom of variable diameter monopile
提取不同桩径下桩身的侧摩阻力分布如图8所示。可以看出,底部桩径增大对外侧摩阻力影响较大,二者成负相关关系,尤其对于DB=9.0 m 的大直径方案;分布规律上,较小桩径下外侧摩阻力随埋深变化基本呈线性增大,底部桩径增大到9.0 m时,外侧摩阻力分布较为均匀,随埋深变化较缓。不同底部桩径条件下内侧摩阻力均集中在40~50 m 桩基埋深处,且随底部桩径增大,桩基内侧摩阻力逐渐减小,底部桩径增大到9.0 m时,内侧摩阻力减小了约12 kPa。因此在进行桩基设计时应考虑底部桩径变化对侧摩阻力的影响。

图8 不同变径桩底部桩径条件下侧摩阻力分布图Fig.8 Side friction resistance distribution under different pile diameters at bottom of variable diameter monopile
3.2 变径段上部长度影响
考虑变径段上部长度变化范围为10~55 m,并保持其他参数不改变。当变径段上部长度增大到55 m时,该桩基为大直径扩底桩。由此得到不同方案下的荷载-沉降曲线如图9(a)所示。从图9中可以看出,随着上部长度增大,使桩基沉降到同一位移所需的荷载逐渐减小,但减小量较小。同时,桩基竖向极限承载力出现小幅度降低。
在桩基顶部施加30 MN 竖向荷载,得到桩身轴力分布图9(b)所示,可以看出变径段上部长度对桩身轴力分布的影响不大。

图9 变径桩变径段上部长度影响Fig.9 Influence of upper length of the variable diameter section of variable diameter monopile
图10展示了不同变径段上部长度方案中各承载分量的变化。由图10可知,随着变径段上部长度增大,外侧摩阻力呈现减小趋势,而内侧摩阻力则逐渐增加。变径段上部长度为55 m时,桩外侧摩阻力承载降幅约为9%,桩内侧摩阻力增加率达到62%,而桩端阻力没有明显变化。
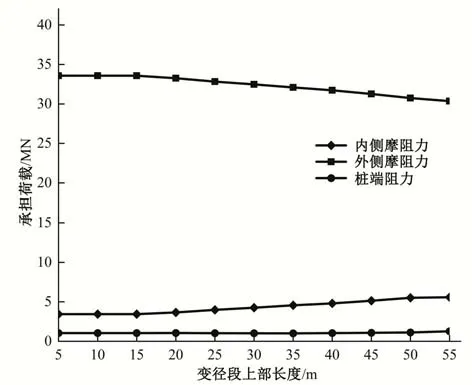
图10 不同变径段上部长度条件下承载分量变化曲线Fig.10 The variation of the component of the bearing load under different upper lengths of the variable diameter section
进一步,提取桩身侧摩阻力应力分布如图11所示。变径段上部长度的变化对桩身外侧摩阻力没有明显影响,而桩内侧摩阻力值随变径段上部长度增加而逐渐提高。

图11 变径段上部长度条件下侧摩阻力分布图Fig.11 Side friction resistance distribution under different upper lengths of the variable diameter section
3.3 变径段长度影响
考虑变径段长度变化范围为10~60 m,并保持其他参数不改变,以研究变径段长度对桩基础竖向承载特性的影响。不同方案下的荷载-沉降曲线如图12(a)所示。由图12可知,随着变径段长度增大,使桩基沉降到同一位移所需的荷载小幅度减小,但桩基竖向极限承载力基本不改变。在桩基顶部施加30 MN 竖向荷载,得到桩身轴力分布如图12(b)所示。从图12中可以看出,不同变径段长度下桩基泥面以下的轴力分布也基本相同,变径段长度对桩基轴力分布无明显影响。
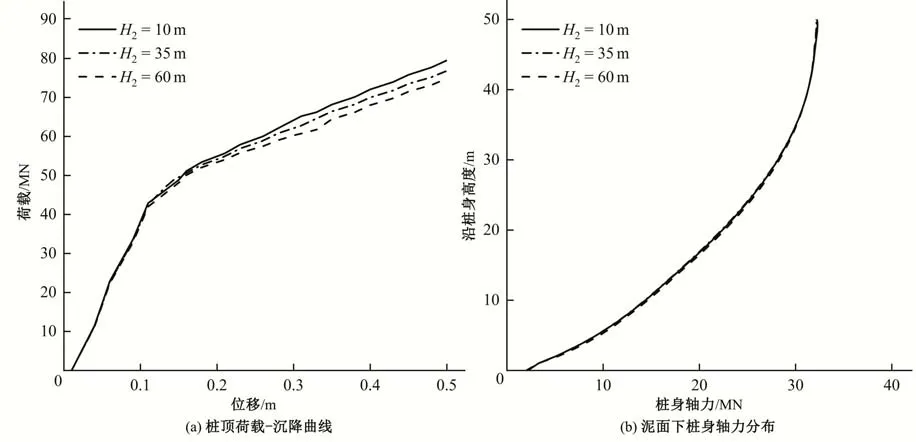
图12 变径桩变径段长度影响Fig.12 Influence of length of variable diameter section of variable diameter monopile
图13显示了不同变径段长度方案中各承载分量的变化。当竖向荷载值为30 MN 时,随着变径段长度增大,内侧摩阻力逐渐提高,而外侧摩阻力则逐渐降低。当变径段长度达到60 m时,桩外侧摩阻力降低率约为4%,桩内侧摩阻力增加率约为37%,而桩端阻力没有明显变化。
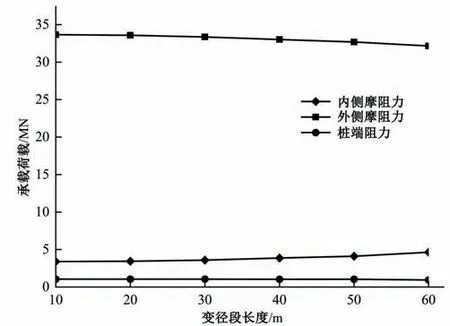
图13 不同变径段长度条件下承载分量变化曲线Fig.13 The variation of the component of the bearing load under different lengths of the variable diameter section
不同变径段长度桩基的内外侧摩阻力分布如图14所示。由图14可以看出,随变径段长度增大,桩基外侧摩阻力明显增大,但变径段长度增大到35 m 后,再增大变径段长度外侧摩阻力变化不明显;内侧摩阻力与变径段长度间关系与外侧摩阻力基本一致。

图14 不同变径段长度条件下侧摩阻力分布图Fig.14 Side friction resistance distribution under different lengths of the variable diameter section
4 结 论
本文通过数值模拟方法,对比了海上风机通长桩基础与变径桩基础间的竖向承载力差异,并分析了变径段尺寸参数对变径桩基础承载能力的影响,得出主要结论如下。
(1)与通长桩相比,在相同竖向荷载作用下,变径特性基本不影响桩基础的桩身轴力分布。当竖向荷载较小时,桩身外侧摩阻力承担主要荷载,变径桩和通长桩各分量的承载值与施加的竖向荷载基本呈线性关系,但占比保持不变;当竖向荷载超过40 MN 时,内侧摩阻力与桩端阻力大幅增加,外侧摩阻力增幅放缓,且变径桩基础外侧摩阻力承载比大于通长桩,而桩端阻力承载比小于通长桩。
(2)提高变径桩底部桩径,可显著提高桩基竖向极限承载力以及外侧摩阻力承载占比,而桩端阻力和内侧摩阻力承载比则将小幅降低。
(3)变径段长度及变径段上部长度对桩基竖向极限承载力影响有限,二者主要影响侧摩阻力的分布与承载分量占比;提高二者长度会小幅降低桩基竖向极限承载力,并降低外侧摩阻力承载比。
(4)若在实际工程中采用变径桩基础,建议适当提高底部直径以提高桩基础的竖向承载力;同时当变径段没入泥面后,增大变径段长度或变径段上部长度会增大内侧摩阻力的发挥,因此在设计时若变径段较大比例没入土体内,则应考虑内侧摩阻力的影响。
