台阶式溢洪道数值模拟计算精度评价方法

2023-02-28王海波沈立群张晋锋武英豪

中国农村水利水电 2023年2期

王海波，沈立群，张晋锋，武英豪

（1.湖北省水利水电规划勘测设计院，湖北武汉 430064；2.武汉大学水利水电学院，湖北武汉 430000）

0 引言

得益于碾压混凝土技术（RCC）的应用，台阶式溢洪道已经成为国内外水利工程中通用的泄流消能方式。由于水流沿程逐级掺气、减速、消能，与光滑溢洪道相比，台阶式溢洪道能够显著减轻下游的消能压力。空气掺入水流形成的水汽二相流复杂运动是台阶式溢洪道数值模拟计算的难点。

随着CFD 领域和计算机技术的发展，数值误差评估方法也在不断更新迭代，目前最可靠的是RE（Richardson Extrapolation）法［1，2］。自从它的创始人于1911年首次提出该方法以来，大量学者对其进行研究并应用到数值误差评估中［3，4］。美国机械工程师协会（American Society of Mechanical Engineers，ASME）的流体工程部一直致力于CFD 数值误差的检测和评估的工作。CFD 可靠性分析领域的第一套质量控制措施是由该部门的Roache 等人［5］于1986年发布，并由Freitas［6］于1993年进行修订。它就是基于RE 法的计算网格收敛指数法（Grid Convergence Index，GCI），该方法已应用在数百个CFD 案例中［7］。采用从致密至粗糙3 种网格尺寸，利用Flow 3D®软件对台阶式溢洪道上的水汽二相流进行数值模拟，提供评价其计算精度的一般方法。采用从致密至粗糙3 种网格尺寸，利用Flow 3D®软件对台阶式溢洪道上的水汽二相流进行数值模拟，提供评价其计算精度的一般方法。

1 试验方案与方法

本次数值模拟的计算域包括上游水库段、宽顶堰段、台阶式溢洪道段和尾水渠段。为保障计算精度的同时加快计算速率，数值模拟采用二维网格进行计算。以水库底部起点为坐标原点，上游至下游水平方向为X轴正方向，竖直向上为Y轴正方向，计算模型的全局体型见图1。为保障上游水库水位稳定，水库长度取为37.5 m；为保障台阶段入流平顺，在其前方设置长度为20.625 m 的宽顶堰；尾水渠段长度取为12.5 m。台阶高度为1 m，步长为1.25 m，坡度为38.66°，共25级台阶。

图1 计算模型全局示意图（单位：m）Fig.1 Global schematic diagram of the computational model

Flow 3D®软件是基于混合框架并兼具模拟以上4 种物理现象的能力。它采用GMRES 方法［8］求解离散方程，采用Favor 技术［9，10］进行网格处理，可实现用简单的结构化网格描述复杂的几何体型［11］，并开发了Tru-VOF 方法［12］，大幅改进了其追踪自由液面的速度和精度。因此，本文选用Flow 3D®软件对台阶上的水汽二相流进行数值模拟计算。

2 网格收敛指数计算步骤

一般而言，网格越密集，GCI 越小，代表计算结果越精确。GCI 法至少需要从致密到粗糙的3 种网格，本试验计算网格收敛性分析取网格尺寸为：0.037 5 m×0.037 5 m（网格1：h1×h1）、0.05 m×0.05 m（网格2：h2×h2）、0.066 7 m×0.066 7 m（网格3：h3×h3），即网格加密因子r取为：

大于推荐的最小网格加密因子1.3［13］。GCI 法的计算步骤为：

（1）计算收敛精度p。

式中：φk为第k种网格下数值模拟计算的离散解。本试验中r21=r32=1.333，可得q(p)=0，进而简化收敛精度p的计算。

（2）计算网格2相对于细密网格（网格1）的相似误差。

（3）计算网格2相对于细密网格（网格1）的网格收敛指数。

3 计算网格收敛性分析

台阶式溢洪道中，水面线及流速是描述水流的基本参数，湍动能是决定水流自掺气是否发生的关键水力参数，在数值模拟计算中必须保证这3个参数的准确性。本节以1.25 m均匀步长台阶方案在hk∕h=2.0 流量工况下的水面线、流速和湍动能作为特征离散解，采用GCI方法进行计算网格收敛性分析。

3.1 水面线

Flow 3D®软件在3 种网格下计算所得的水库及宽顶堰水面线［图2（a）］、台阶段水面线［图2（b）］均贴合紧密，即3 种网格的整体水面线之间相差甚微，仅在溢洪道后半段观察到轻微的离散。将5、10、15、20 号台阶上方的水面线进行局部放大［图2（c）～（f）］，可知3 条水面线之间在15 号台阶前贴合紧密，在20号台阶上开始观察到轻微的离散：细密网格（网格1）的水面线最高，粗糙网格（网格3）的水面线最低，网格2 的水面线介于两者之间。网格越细致，掺气模型捕捉到的掺气就越多，掺气水深增高，水面线被抬升，而台阶式溢洪道的掺气充分发展区一般位于后半段，这才使得3 种网格的水面线之间在20 号台阶之后出现轻微的离散。

图2 不同网格尺寸的计算水面线对比Fig.2 Comparison of water surface lines calculated with different grid sizes

网格2 计算水面线与细密网格（网格1）计算水面线之间的偏差已十分微小。以20号台阶上水面线数据为离散特征解，采用GCI方法对其进行数值误差评估（图3），得出网格2的全局网格收敛指数小于5%。最大GCI21为4.01%，出现在x=82.125 m，对应细密网格计算水深为2.23 m。

图3 网格2计算水面线对应的网格收敛指数（20号台阶）Fig.3 The GCI corresponding to the water surface line calculated by NO.2 grid

3.2 流速

Flow 3D®软件采用3种网格计算所得的5、10、15、20号台阶顶（凸角处）竖直断面上的流速分布如图4，均呈现由底部向水面逐渐增大的正确分布规律。网格2断面流速曲线与细密网格（网格1）断面流速曲线之间贴合紧密，而与粗糙网格（网格3）断面流速曲线之间存在明显偏差。细密网格能够更加充分考虑水流掺气对流速发展的影响，更加精确捕捉空间上流速的变化。一般而言，同一位置处细密网格计算流速略大于粗糙网格计算流速，且细密网格的断面流速梯度大于粗糙网格的断面流速梯度。

图4 不同网格尺寸的台阶顶竖直断面计算流速对比Fig.4 Comparison of calculated velocity in vertical section of convex corner with different grid sizes

网格2计算流速与细密网格计算流速之间的偏差已十分微小。以5、10、15、20 号台阶顶竖直断面上的流速数据为离散特征解，采用GCI 方法对其进行数值误差评估（图5），得出网格2的全局网格收敛指数小于5%。5号台阶最大GCI21为1.56%，出现在y+=0.3 m，对应细密网格计算流速为8.82 m∕s；10 号台阶最大GCI21为2.33%，出现在y+=0.1 m，对应细密网格计算流速为7.46 m∕s；15号台阶最大GCI21为3.53%，出现在y+=0.2 m，对应细密网格计算流速为8.88 m∕s；20号台阶最大GCI21为3.29%，出现在y+=0.9 m，对应细密网格计算流速为14.58 m∕s。

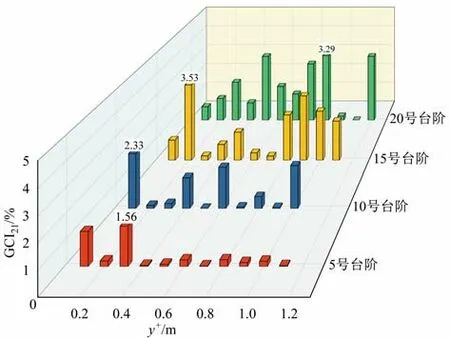
图5 网格2计算流速对应的网格收敛指数Fig.5 The GCI corresponding to the velocity calculated by NO.2 grid

3.3 湍动能

Flow 3D®软件采用3种网格计算所得的5、10、15、20号台阶顶竖直断面上的湍动能分布如图6，均呈现由底部向水面逐渐减小的正确分布规律。与流速计算结果类似，网格2 断面湍动能曲线与细密网格（网格1）断面湍动能曲线之间紧密贴合，而与粗糙网格（网格3）断面湍动能曲线之间存在明显差异。细密网格能够通过Favor 技术更加准确还原台阶的体型轮廓，更加精确进行湍流模型的计算。同一位置处细密网格计算湍动能大于粗糙网格计算湍动能。

图6 不同网格尺寸的台阶顶竖直断面计算湍动能对比Fig.6 Comparison of calculated turbulent kinetic energy in vertical section of convex corner with different grid sizes

网格2计算湍动能与细密网格计算湍动能之间的偏差已十分微小。以5、10、15、20 号台阶顶竖直断面上的湍动能数据为离散特征解，采用GCI 方法对其进行数值误差评估（图7），得出网格2 的全局网格收敛指数小于5%。5 号台阶最大GCI21为4.1%，出现在y+=0.8 m，对应细密网格计算湍动能为0.18 m2∕s2；10 号台阶最大GCI21为3.4%，出现在y+=0.6 m，对应细密网格计算湍动能为1.46 m2∕s2；15号台阶最大GCI21为3.84%，出现在y+=0.6 m，对应细密网格计算湍动能为2.48 m2∕s2；20 号台阶最大GCI21为2.56%，出现在y+=1.0 m，对应细密网格计算湍动能为2.02 m2∕s2。

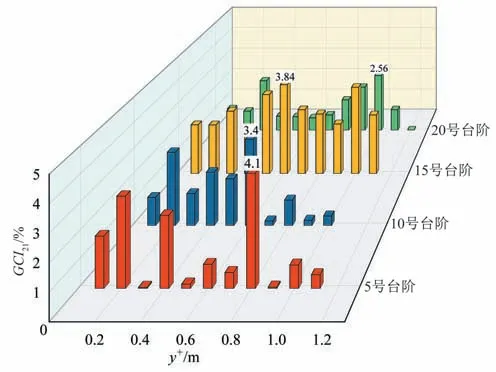
图7 网格2计算湍动能对应网格收敛指数Fig.7 The GCI corresponding to the turbulent kinetic energy calculated by NO.2 grid

3.4 网格尺寸确认

通过分别以水面线、流速和湍动能作为离散特征解进行的网格收敛性分析可知，网格2 计算结果与细密网格（网格1）计算结果之间的偏差较小，3 种水力参数对应的全局GCI21均小于5%；粗糙网格（网格3）计算水面线与细密网格（网格1）计算水面线之间的偏差也较小，但两者的计算流速和湍动能之间存在较大偏差。为保障计算精度的同时缩减计算时长，本文所涉及的数值模拟均采用网格2（0.05 m×0.05 m）尺寸进行计算，即每个台阶在高度方向上被均分为20个网格，如图8。

图8 推荐计算网格尺寸示意图Fig.7 Schematic diagram of recommended calculation grid size

4 数值模拟精确性分析

本文以张文传［14］进行的1.25 m 均匀步长台阶方案的物理模型试验测量数据作为参照，选用水面线、流速和初始掺气点作为比较参数，评价数值模拟计算结果的精确度。物理模型长度比尺为1∶12.5，模型台阶高度和步长分别为8 cm和10 cm。

4.1 水面线验证

hk/h=2.0流量工况下，1.25 m均匀步长台阶方案通过数值模拟计算和物理模型试验测量所得的宽顶堰上水面线、台阶段上水面线分别如图9、图10，其中B表示宽顶堰长度。

图9 数值模拟计算与物模试验实测的宽顶堰上水面线对比Fig.9 Comparison between numerical simulation calculation and physical model test measurement of water surface line on wide-top weir

图10 数值模拟计算与物模试验实测的台阶段上水面线对比Fig.10 Comparison between numerical simulation calculation and physical model test measurement of water surface line on stepped spillway

宽顶堰上数值模拟计算水面线与物模试验实测水面线之间整体贴合紧密，仅在前半部分出现少许离散，后半部分及溢洪道入流部分几乎无偏差。两者的最大偏差出现在x∕B=0.1处，为2.8%，对应物模试验实测水深为2.613 m。

台阶段上数值模拟计算水面线与物模试验实测水面线之间整体贴合紧密，两者在台阶段前半段几乎无偏差，却在后半段出现少许离散。前半段水流未掺气，为纯水流流动，或掺气浓度较低，数值模拟计算精度较高，同一位置处计算水面线略低于物模试验实测水面线，两者偏差均不超过5%；后半段水流掺气逐渐发展，水汽二相流的运动特性更加复杂，数值模拟计算精度有所下降，同一位置处计算水面线略高于物模试验实测水面线，两者最大偏差出现在x=89.375 m 处，为12%，对应物模实测水深为1.5 m。

4.2 流速验证

hk/h=2.0 流量工况下，分别取1.25 m 均匀步长台阶方案在5、10、15、20 号台阶顶竖直断面的数值模拟计算流速与物模试验实测流速进行对比（图11）。

图11 数值模拟计算与物模试验实测的台阶顶竖直断面流速对比Fig.11 Comparison between numerical simulation calculation and physical model test measurement of vertical section of convex corner

数值模拟计算与物模试验实测的台阶顶竖直断面流速分布规律相同，即自底部至水面的流速逐渐增大、流速梯度逐渐减小。在水流底部，物模试验实测流速大于数值模拟计算流速，在水流表面，却正好相反，即在同一竖直断面上，物模试验实测的流速梯度小于数值模拟计算的流速梯度，与前人研究结果一致［11］。物模试验实测流速与数值模拟计算流速之间在5号台阶顶竖直断面上的偏差很小，不超过5%，后在10、15、20号台阶顶竖直断面上的偏差逐渐增大。数值模拟计算未充分考虑水流掺气导致水流底部与台阶面之间的摩擦减小这一效果，随着水流掺气的沿程发展，这一缺陷会导致数值模拟计算流速与物模试验实测流速之间的偏差被逐渐拉大。两者之间的最大流速偏差出现在20 号台阶底部，为16%，对应物模试验实测流速为9.0 m∕s。

4.3 初始掺气点验证

初始掺气点作为水流表面掺气的起点，是描述水流自掺气的关键参数，需确保CFD 软件对其位置模拟的可靠性。hk/h=1.2、hk/h=1.4、hk/h=1.6、hk/h=1.8、hk/h=2.0 五种流量工况下，分别取1.25 m 均匀步长台阶方案数值模拟计算的初始掺气点位置与物模试验实测的初始掺气点位置进行对比，以评价Flow 3D®软件内嵌掺气模型的计算精度。初始掺气点后水流迅速掺气，湍动加剧，空气和水混合，呈现为乳白色的水汽二相流［14］（图12）。物模试验中可将水流表面开始变白的位置作为初始掺气点。数值模拟可绘制水流的掺气浓度云图（图13），可以清晰观察到初始掺气点的位置［15，16］。