基于相轨迹的机组阻尼系数最小二乘量化方法
2023-02-28陆雪顶王光政
郭 岐,陆雪顶,王光政
(1.华北水利水电大学电力学院,河南 郑州 450045;2.华中科技大学土木与水利工程学院,湖北 武汉 430074)
0 引 言
随着清洁能源大规模并网和各区域电力系统的互联,以低频振荡为代表的动稳定问题日益凸显。工程表明,超低频振荡问题在水电为主导的电力系统中尤为突出,其中以云南电网为典型代表的多个高水电占比电力系统均发生过超低频振荡现象[1-3]。不仅国内,美国、土耳其、加拿大等国的电网也出现过超低频振荡现象[4-6]。相比低频振荡,超低频振荡的振荡频率更低,其频率低于0.1 Hz,且影响范围更广,振荡为整个区域的公共振荡[7]。
研究电力系统超低频振荡广泛采用的方法有模式分析法和阻尼转矩法[8,9]。其中,模式分析侧重于指导设计,对振荡产生机理的解释不足,而阻尼转矩法物理意义明确,能更好的解释系统低频振荡的机理[10]。文献[11]指出负阻尼作用是导致系统超低频范围不稳定的重要成因,并通过分析阻尼对系统参数敏感性,评估参数对系统超低频振荡的影响程度。文献[12]设计了超低频振荡附加阻尼控制器,并以阻尼为指标优化控制器控制参数,实现了超低频振荡的抑制。此外,许多学者们以附加阻尼控制为思路,在水轮机调节系统控制器参数的优化与相位补偿控制器的设计等方面取得了积极的成果[13-15]。总体而言,阻尼系数是系统超低频振荡分析的重要指标,有效量化机组的阻尼对控制参数的优化与系统的设计都至关重要。
传统的阻尼系数计算方法利用原动机系统开环频率特性进行计算,依赖线性系统传递函数表达式,难以适应强非线性系统[16]。因此,研究人员在非线性系统阻尼量化评估上开展了积极的研究。马骞等提出一种基于超低频振荡录波曲线的阻尼系数量化方法[17],通过测量功率、频率的正弦特征有效地实现实际机组阻尼的快速量化,但计算仅依赖于少量的峰值数据,在抗干扰性与评估准确性存在不足,适合系统的在线阻尼评估。刘冬等利用“频率-功率”相轨迹来量化机组阻尼[18],利用批量的时域数据,整体评价系统的阻尼特性,方法抗干扰性强、准确性高,但量化需要经过相图绘制、轨迹平移和梯度下降寻优等步骤,操作复杂、计算繁琐,方法适合强非线性系统离线阻尼评估。
综上所述,现有的阻尼系数量化方法在对强非线性系统评估时难以兼顾计算准确性与操作简便性,亟需提出一种能适用于强非线性系统、抗干扰性强且操作简便的阻尼转矩量化方法。
本文首先分析了超低频振荡机组的阻尼特性,利用阻尼转矩理论推导出基于相轨迹最小二乘拟合的机组阻尼量化方法;其次,通过量化值与理论值对比和多机系统超低频振荡分析验证了方法的计算准确性和有效性;最后,利用实际机组的监测信号校验了该量化方法对强非线性系统的适用性。
1 超低频振荡机组阻尼分析
1.1 单机系统阻尼特性
原动机调节系统一般由调速器和原动机组成,如图1所示,Ggov(s)为调速器线性模型,GH(s)为原动机线性化模型。设原动机调节系统的传递函数为G(s),系统的传递函数模型为:

图1 原动机调节系统线性化模型Fig.1 The linearized model of turbine governing systems
式中:G(s)=Ggov(s)GH(s),Δω为转速增量,ΔPm为原动机机械功率增量。
基于Phillips-Heffron模型,将s=jω带入式(1)得:
式中:Dm为阻尼转矩系数,是ΔPm在Δω轴的分量;Km为同步转矩系数,是ΔPm在Δδ轴方向的分量。
ΔPm的分解如图2所示。
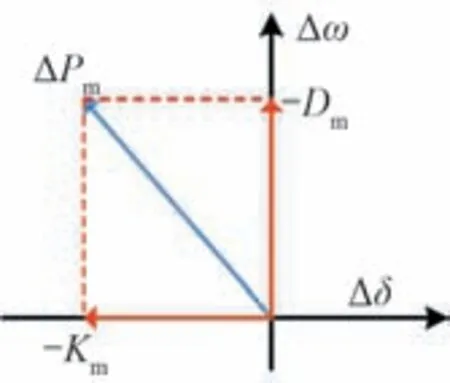
图2 ΔPm分解示意Fig.2 The decomposition of ΔPm
以水电机组为例,为了便于分析,仅考虑功角变化引起的电磁转矩变化,同步发电机的二阶运动方程为:
式中:Δδ为发电机功角增量,Δω为发电机角速度增量,ω0为发电机同步角速度,ΔPm为发电机机械功率增量,ΔPe为发电机电磁功率增量,D为发电机阻尼系数,Ta为机组惯性时间常数。
如果忽略网络损失,可近似认为电磁增量等于有功增量即:
式中:ΔPL为发电机有功增量;KL为负荷频率调节系数。
将式(2)和式(4)带入式(3)得:
由式(5)可知系统的阻尼比为:
式中:KL与D为常数,Dm的大小将影响系统的阻尼特性。
结合ΔPm分解图2与式(6)可知Dm的作用十分明确:当Dm<0 时,-Dm与Δω同向,调速系统Δω起促进作用,ξ减小,这将加剧系统频率振荡。相反,当Dm>0,-Dm与Δω方向相反,ξ增加,这将抑制系统振荡。所以,当Dm<0时,调速原动系统向系统提供负阻尼,Dm>0时调速原动系向系统提供正阻尼。
1.2 多机并列运行频率调速系统阻尼特性
为便于分析多机组并列运行情况下原动机调节系统,可假设各并网运行机组保持严格的同步运行,即“刚性联结”假设,此时可以把所有参与频率调节的机组折算为一台等效机组[19],如图3所示。系统机组总功率偏差为:
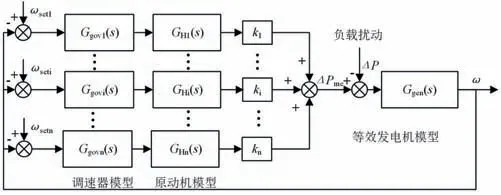
图3 “刚性联结”多机运行系统线性化模型方框图Fig.3 Block diagram of linearization model of the multi-machine operating system with “rigid coupling”
式中:ΔPme为并列机组等效机械功率偏差;i为调频机组的编号;ki为i机组额定出力占系统总容量的比重。
计算多机系统的阻尼转矩系数为:
式中:Dme为多机系统原动机提供的等效阻尼转矩系数;Dmi为i原动机系统提供的阻尼转矩系数。
与单机分析类似,等效系统的阻尼比为:
式中:ξe为系统的等效阻尼比;KLe为等效同步转矩系数;KLe为等效系统的等效负荷频率调节系数;De为等效发电机阻尼系数。
由式(8)和式(9)可知,多机原动机系统中各机组向系统提供阻尼转矩系数满足线性叠加关系,系统总的阻尼比与各原动机系统提供的阻尼转矩系数也是线性关系。因此,准确量化各调频机组的阻尼转矩系数,对于超低频振荡发生原因的定位与消除十分必要。
2 机组阻尼转矩量化方法
2.1 方法原理
对开环线性系统给定频率的正弦输入,稳态后系统输出响应也为正弦扰动[20],如图4所示。对ΔPm∕Δω进行如式(10)的推导。

图4 线性系统频率正弦扰动稳态响应Fig.4 Steady-state response of linear systems under frequency sine frequency disturbance
式中:ωa为正弦扰动频率;A为幅频特性;θ为相频特性;A和θ分别是关于ωa的函数A(ωa),θ(ωa)。
推导的几何意义是先将Δω和ΔPm两个信号映射在Δω-ΔPm相平面中,然后对相轨迹进行求导以求取相轨迹斜率,最后将相轨迹的斜率分解为一个常量Acos(θ(ωa))和周期量sin(ωat)sin(θ)。因此,对于任意确定ωa的正弦扰动响应,Δω- ΔPm相轨迹的斜率由固定的斜率Acos(θ(ωa))和随时间周期变化的f(θ,ωa,t)斜率叠加得到。结合阻尼系数表达式即式(2)可知,相轨迹固定的斜率就是阻尼转矩系数即Dm=Acos(θ(ωa))。因此,相图上一定可以找到斜率为Dm的唯一直线来表征系统的阻尼系数,如图5所示。

图5 相轨迹斜率组成Fig.5 Composition of the slope of the phase trajectory
对于强非线性系统,无法通过求取开环传递函数实部的方式获得阻尼转矩系数,但是可通过测量∕仿真的方式,得到系统的Δω- ΔPm相轨迹。利用式(10)的相轨迹斜率分解思想,可寻找到唯一的最优的直线,直线斜率表征系统的阻尼转矩系数Dm。由于相轨迹斜率是由固定值和周期值叠加而成,因此可以采用最小二乘法拟合这条最优的直线,使得该直线的均方误差最小,如式(11)所示:
式中:Xi为相图上第i点的Δωi所对应的ΔPm_i值;X′i为直线上第i点的Δωi所对应的ΔPm_i值。
2.2 量化流程
依据最小二乘法量化机组阻尼系数的原理可写出阻尼系数快速量化方法的流程,如图6所示,详细流程如下:
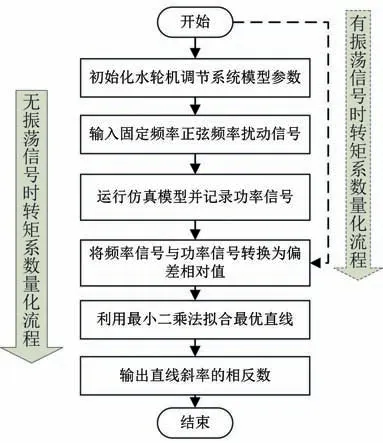
图6 阻尼量化流程Fig.6 Process of the damping quantification method
(1)初始化原动机调节系统仿真模型;
(2)输入固定频率的正弦频率扰动负反馈;
(3)对原动机调节系统进行时域仿真,并记录功率信号;
(4)将频率信号和功率信号转换为偏差相对值;
(5)利用最小二乘法将转换后的频率信号和功率信号拟合为直线;
(6)输出直线斜率的相反数即为原动机系统提供的阻尼转矩系数。
对于搭建的原动机系统仿真模型,如果没有振荡信号,阻尼量化流程为(1)~(6);如果能够直接采集到频率和功率信号,便可跳过开环系统正弦频率扰动仿真,直接拟合直线便可得到阻尼,其步骤为(4)~(6)。
3 算例分析
本部分将利用单机模型、多机模型以及实际系统的实测数据来验证基于相轨迹最小二乘拟合阻尼量化方法的准确性、有效性与适用性。
3.1 算例1:单机系统阻尼量化分析
为了验证该量化方法的精度,以简化的理想水轮机调速系统模型为对象,如图7所示。将量化的阻尼系数和机组阻尼系数的理论值进行对比,以计算0.01~2.5 Hz频率范围内对应阻尼系数为例,频率计算步长设置为0.01 Hz,重复给定不同频率的正弦频率扰动信号,计算各振荡频率下的阻尼系数,阻尼系数的理论值由开环系统的幅频特性计算得到。理论值与量化值对比如图8所示。
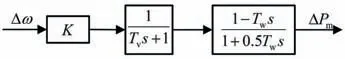
图7 简化水轮机调节系统Fig.7 Simplified hydro-turbine regulation systems
由图8可知,基于相图的阻尼系数最小二乘量化方法得到的阻尼量化值曲线与阻尼理论值曲线十分契合,误差维持在10-4左右,这表明方法能准确计算出机组的阻尼转矩系数。

图8 最小二乘量化的阻尼与理论阻尼的对比(K=20,Tv=2,Tw =1)Fig.8 Comparison of quantified damping values with theoretical damping values (K=20,Tv=2,Tw =1)
3.2 算例2:4机系统阻尼量化分析
为了进一步分析方法在多机系统中的有效性,基于MATLAB∕Simulink2020b 建立了一个高水电占比的4 机并列运行系统,如图9所示。其中,1~2号为同型火电机组,3~4号机组为同型水电机组,所有机组的额定容量均为700 MW,机组初始运行在额定工况。
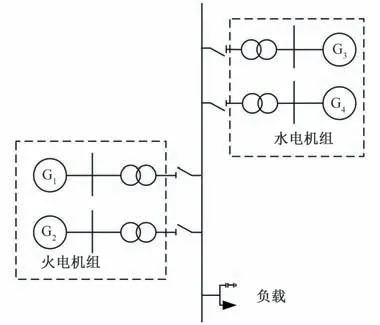
图9 4机并列运行系统Fig.9 Four-machine parallel operating systems
1~3 号机组控制参数设计为实际值,通过改变4 号机组调速器参数将其设置为负阻尼机组,并使系统处于临界稳定状态。在0.1 s 时,对系统施加+1%的负载扰动,系统产生了频率约0.05 Hz 的超低频振荡,在87.5 s 时对4 号机组设置人工死区使其退出调频,系统恢复稳定。利用0~80 s 内1~4 号机组的频率和功率信号,分别对各机组的“功率-频率”信号进行最小二乘量化。系统的频率响应与各机组的阻尼量化如图10所示。
由图10可知,1~3 号机组“频率-功率”相轨迹向下倾斜,均向系统提供正阻尼;而4号机组相轨迹向上倾斜,阻尼转矩系数为-0.997 2,其在振荡的过程中向系统提供负阻尼。从阻尼转矩系数的角度分析,4号为系统超低频振荡的诱发机组。因此,在87.5 s 时退出4 号组的调频,系统便可恢复稳定。进一步,将四台机组量化的阻尼系数进行线性叠加,计算系统的等效阻尼系数Dme=-0.030 9,结合仿真系统中KL=0.03,D=0,k1=k2=k3=k4=0.25 的设置信息,由式(9)可以计算出系统的阻尼比ξe=-0.000 9,所以系统基本处于临界稳定状态。主导机组的定位验证与阻尼比的验算均表明所提方法在多机系统中应用十分有效。
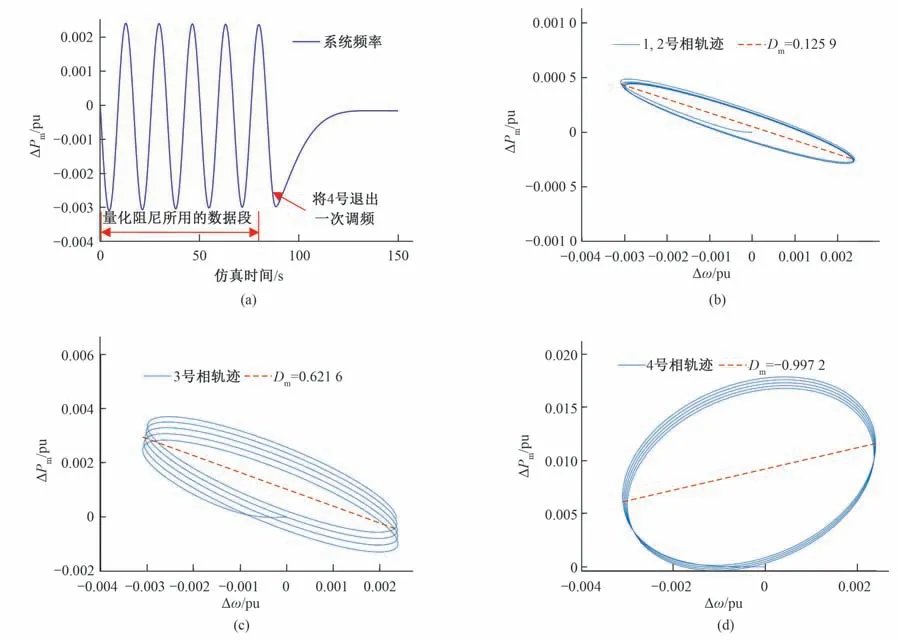
图10 4机并列运行系统仿真与阻尼量化Fig.10 Simulation and damping quantification of the 4-machine parallel operation systems
3.3 算例3:实际系统超低频振荡阻尼量化分析
为了验证方法在强非线性系统中的适用性,此部分采用云南电网异步并网小扰动实验时超低频振荡实测数据,对某火电站与某水电站的机组阻尼进行量化。其中机组的基本计算参数如表1所示。水电、火电机组的“频率-功率”实测信号与阻尼转矩系数的量化结果如图11所示。

表1 机组计算参数Tab.1 Calculated parameters of units
由图11可知,水电机组“频率-功率”相轨迹明显向上倾斜,量化的阻尼转矩系数为-7.365 8。工程中如果机组阻尼系数低于-1,便可认为该机组是超低频主导机组[17]。因此,该水电机组在实际的系统振荡过程中提供强负阻尼,是超低频振荡的主导机组之一。同时,由图11(b)可知,火电机组在振荡过程中向系统提供了强正阻尼。整体而言,由于系统火电比例较低而水电比例较高,火电的强正阻尼效应大部分被水电负阻尼效应抵消,因此系统容易产生超低频振荡,这也是云南电网易发生超低频振荡的内在原因。所以,当电网将与该水电机组类似的12台强负阻尼水电机组退出一次调频后,系统的低频振荡得以消除。因此,基于相轨迹的阻尼最小二乘量化方法在实际的强非线性系统的分析中也同样适用。
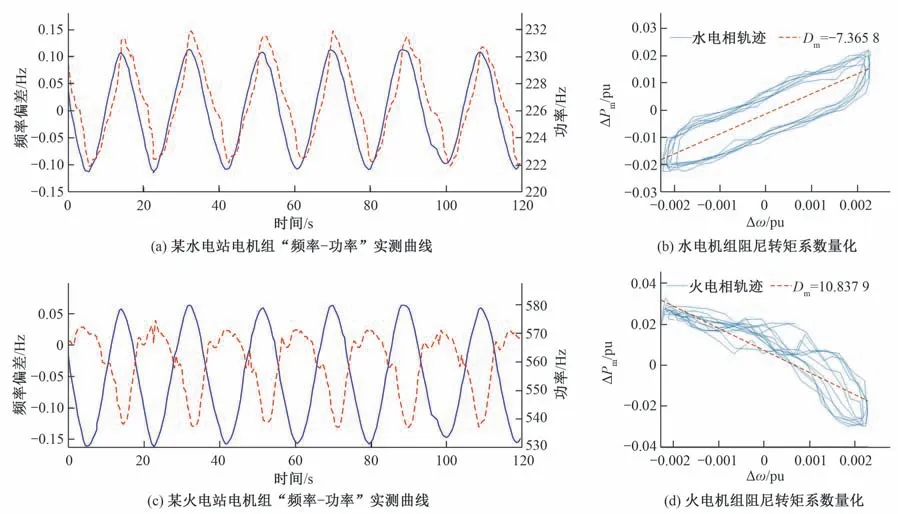
图11 超低频振荡实际机组曲线与阻尼量化Fig.11 Ultra-low frequency oscillation actual unit curve and damping quantification
4 结 论
本文提供了一种原动机系统阻尼转矩系数量化的一般方法,包括相平面映射与最小二乘拟合。经过系列的理论推导与案例计算可得到如下结论。
(1)方法由严格的理论推导得出,操作简单,量化的结果符合阻尼转矩系数的理论定义。
(2)方法的计算精度较高,线性系统量化出的阻尼系数与理论阻尼系数的误差可维持在10-4左右。
(3)通过4机系统案例与实测系统案例的验算,方法能有效量化多机系统和复杂非线性系统的阻尼转矩系数。方法可为实际电力系统中振荡机组的在线监测与复杂非线性系统的阻尼分析提供有效的技术与理论支持。在后续的工作中,将该方法应用在分析系统阻尼对各类非线性因素敏感性上将会是一个重要的研究方向。
