基于内凹三角形负泊松比微结构的汽车B柱优化设计*

赵颖 施劲余 刘轩铭 邓晓钢 郑斯琦

（西南大学，重庆 400715）

主题词：内凹三角形负泊松比微结构 B柱 碳纤维复合材料 聚乳酸复合材料 性能分析

1 前言

B 柱是车体的关键支撑承载件，具有成形深度大、部件截面变化复杂、成形件上下部高度存在起伏等结构特点[1-2]，车辆发生侧面碰撞时，可起到承载和吸能作用，有效保护乘员安全[3]。

张芳芳等[4]考虑侧面圆柱碰撞和移动壁障碰撞工况，采用多因素权重分析和正交试验方法，对车体响应及B 柱材料和厚度参数进行优化，结果表明，B 柱腰线处的侵入速度和侵入量都得到了有效改善，然而，在B柱优化时忽略了轻量化目标。游国忠等[5]建立B柱简化模型，采用拓扑优化和形状优化方法，对B 柱内板结构进行改进，虽降低了其腰线处的侵入速度，但未减轻B柱质量。负泊松比结构具有优异吸能特性，在车辆部件中具有广阔的应用前景[6]。邹松春等[7]基于汽车修理研究协会（Research Council for Automotive Repairs，RCAR）法规和ECE R95法规，分别对传统B柱和负泊松比结构B 柱进行侧面碰撞吸能特性分析，结果表明，与传统B柱结构相比，所设计的负泊松比结构B柱可有效降低侧面碰撞侵入位移和速度。

为满足B 柱对强度、刚度和轻量化特性的需求，本文提出一种新型内凹三角形负泊松比微结构B 柱，其内、外板采用碳纤维复合材料，夹芯层为以聚乳酸椰壳纤维复合材料为基体材料的内凹三角形负泊松比微结构，采用有限元仿真分析方法获得具有最优微拓扑参数的微结构、碳纤维铺层厚度和夹芯层厚度的B柱设计方案，并选取侧向弯曲、后向弯曲、三点弯曲3种典型工况进行对比分析。

2 内凹三角形负泊松比微元胞建模

2.1 代表性微元胞

内凹三角形负泊松比微元胞二维结构如图1所示，其中，L为两腰胞壁长度，N为底边胞壁长度，H、h分别为微元胞和底端平台高度，M为微元胞水平胞壁长度，d为两腰内凹角，δ为底边胞壁与微元胞轴线夹角，c为两腰胞壁与微元胞轴线夹角，a、b分别为微元胞两腰和底边胞壁厚度。将二维微元胞赋予面外厚度i，将二维微元胞沿着Z轴旋转90°并与原二维微元胞交叉形成三维内凹三角形负泊松比微元胞，将三维微元胞分别沿X、Y、Z轴阵列排布，最终形成三维内凹三角形负泊松比微结构。

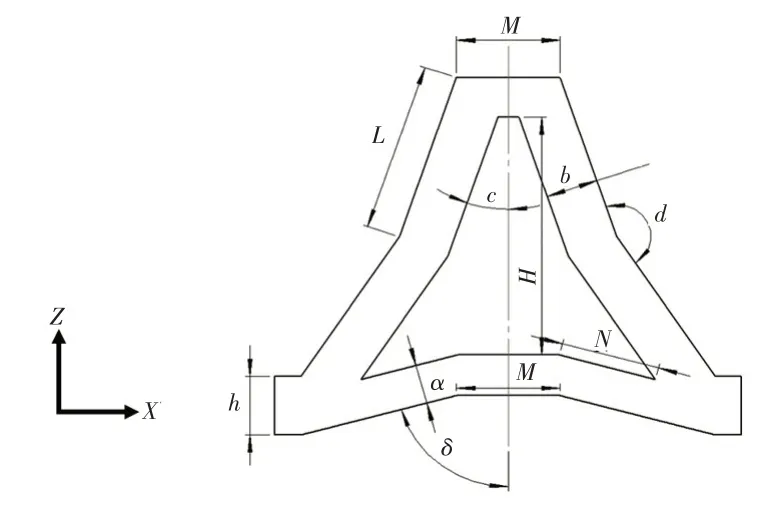
图1 内凹三角形负泊松比微元胞结构

又：

式中，α∈(0,1)为厚度系数；β∈(0,1)为长度系数；γ为宽度系数。

设定胞壁比例系数K=a/b，为保证微元胞呈现负泊松比效应，底端胞壁和两腰胞壁需呈内凹状，因而，140°＜d＜180°，c＞20°。由几何关系可得，长胞壁应完全位于微元胞内，故c＜180°-dmin，即c＜40°，其中dmin为两腰内凹角最小值。根据文献[6]可得K=0.8，为减少多目标优化计算的样本数量并兼顾微元胞的轻质特性，取γ=0.2。

内凹三角形微结构的相对密度越小，质量越轻。因此，可将微结构的轻量化目标转化为其相对密度最小目标。对于三维微元胞，其等效密度ρc与胞壁材料密度ρs的关系为：

因此，三维微元胞的相对密度ρRD,3D可表示为：

式中，V1=i[2bL+a(M+N)+bM/2]为微元胞内胞壁体积；V2=H[M+Lsinc+Lsin(d-c)]2为微元胞体积。

三维微元胞相对密度示意如图2所示。

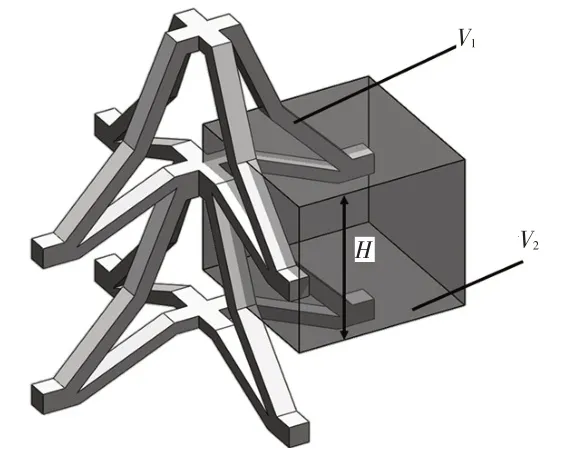
图2 三维内凹三角形负泊松比微元胞相对密度示意

联合式（5）、式（6），可得相对密度ρRD,3D：

其中：

综上，相对密度表达式为：

2.2 仿真分析与试验验证

建立内凹三角形负泊松比微结构的有限元计算模型如图3 所示，为对微结构的冲击动力学特性进行分析，选用Hyperworks-Lsdyna联合仿真方法，基体材料采用聚乳酸椰壳纤维复合材料，密度ρ=1 189 kg/m3，弹性模量E=4.48 GPa，泊松比μ=0.3，屈服应力σ=150 MPa。模型底端节点自由度全约束，刚性墙以冲击速度v=10 mm/min沿Z轴反方向冲击[8]，刚性墙和模型之间的静摩擦因数fs和动摩擦因数fd均设置为0.2。为保证仿真收敛性和计算效率，设定网格尺寸为0.7 mm。

图3 内凹三角形负泊松比微结构有限元模型

采用3D 打印技术打印样件，与有限元模型尺寸一致，内凹三角形负泊松比微结构样件尺寸为260 mm×260 mm×113 mm，其中，α=0.15，β=0.70，c=27°，d=155°，如图4 所示。采用MTS 液压伺服试验机对内凹三角形负泊松比微结构开展准静态压缩试验，MTS液压伺服试验机加载速率与仿真分加载速率保持一致，如图5 所示。

图4 内凹三角形负泊松比微结构3D打印样件

图5 准静态压缩试验设备

在准静态压缩试验过程中，3D 打印样件中的微元胞经历了开始接触、压缩变形、部分微元胞压溃、微结构被完全压溃4 个阶段。选取不同的应变ε，并对仿真结果与试验结果进行对比分析，如图6 所示，仿真工况与准静态压缩试验条件下内凹三角形微结构均呈现明显的“压缩-收缩”的负泊松比变形特性，且变形模式总体保持一致，验证了仿真分析模型的可靠性。

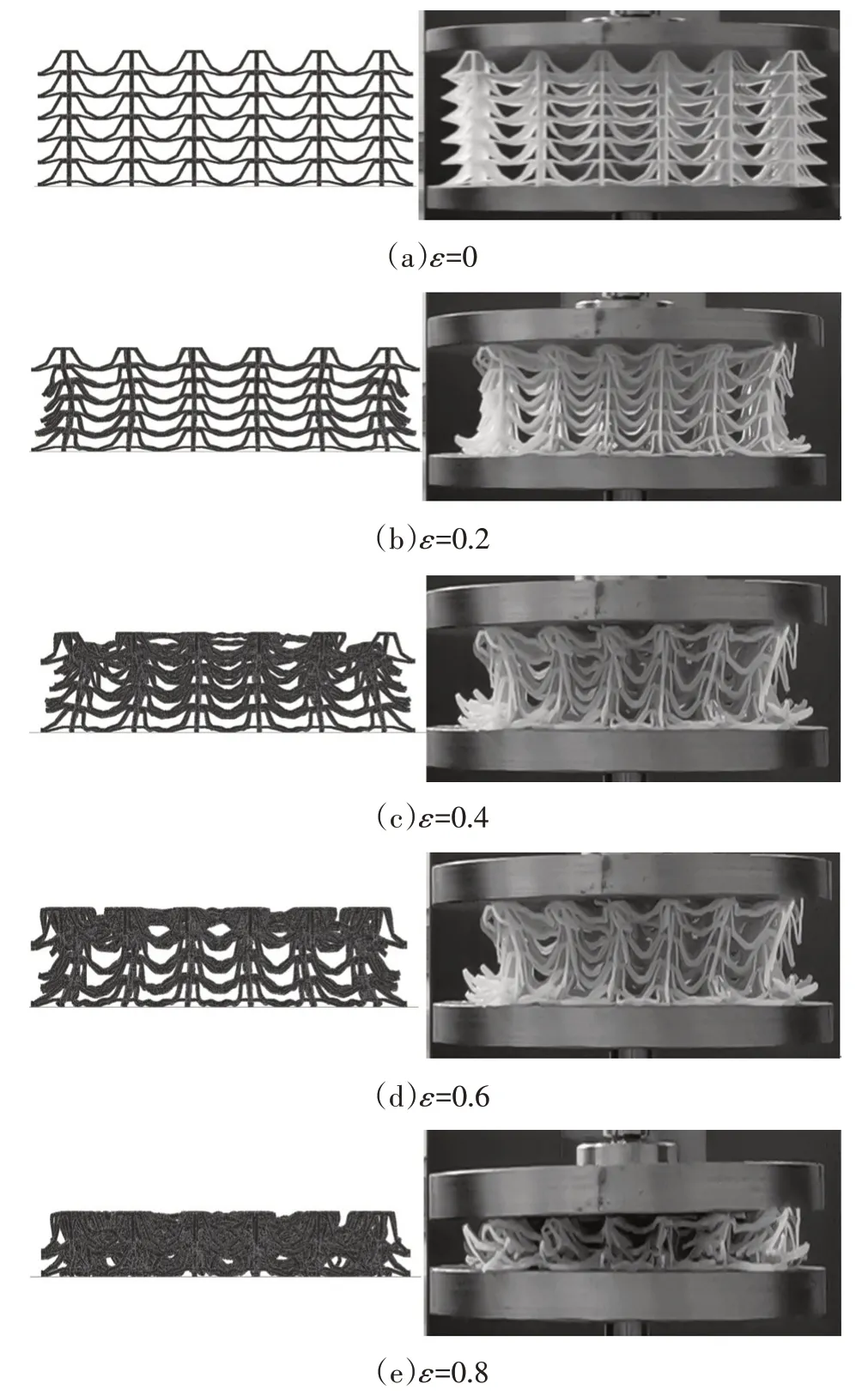
图6 不同的应变条件下仿真分析与准静态压缩试验变形模式对比

同时，可得到有限元仿真分析与准静态压缩试验的应力-应变曲线如图7 所示，由图7 可知，2 条曲线基本吻合，进一步验证了仿真模型的准确性。

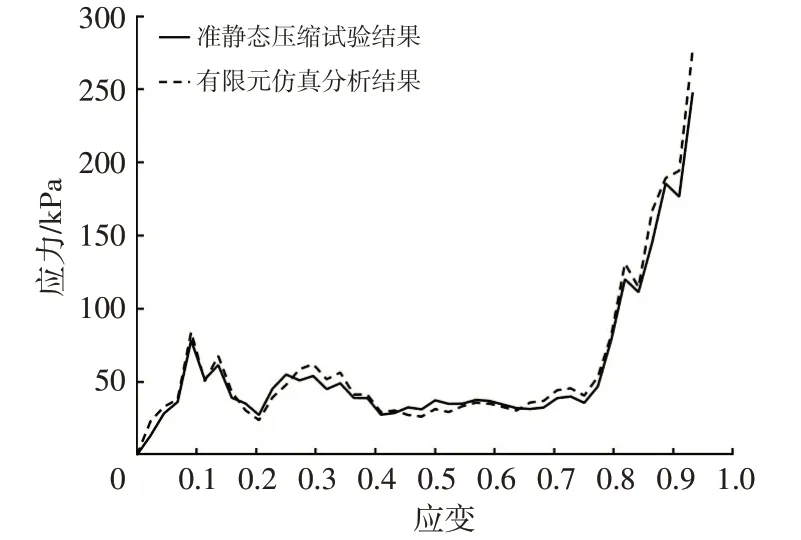
图7 仿真分析与准静态压缩试验应力-应变曲线

为直观反映结构的抗变形能力，绘制有限元仿真分析与准静态压缩试验的力-位移曲线如图8所示。

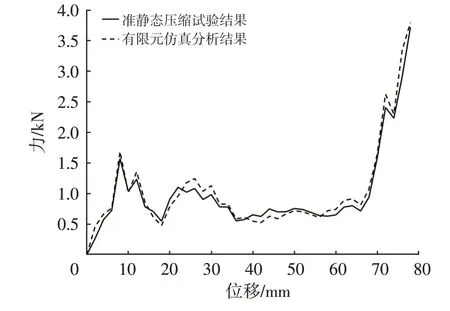
图8 仿真分析与准静态压缩试验力-位移曲线

3 内凹三角形负泊松比微元胞多目标优化

内凹三角形负泊松比微结构在冲击过程中所吸收的能量可由应力-应变曲线与应变坐标轴所包围的面积表示。单位体积吸能量（Specific Energy Absorption，SEA）可表达为：

式中，W为单位体积吸能；εD为密实应变；σ(ε)为瞬时应力。

在特定吸能量条件下，峰值力（Peak Collision Force，PCF）会影响冲击过程中产生的最大碰撞力和最大减速度，PCF越小，微元胞抵抗塑性坍塌的能力越强。

相对密度ρRD,3D表征微结构质量，相对密度越小，轻量化效果越明显。为满足B 柱刚度、强度与轻量化需求，以SEA最大、PCF最小和相对密度最小为优化目标。

响应面法是通过合理的试验设计建立设计变量、优化目标和约束之间的近似函数关系的方法，相对于复杂模型，采用响应面法评估更加简便[9]。综合考虑计算量和计算精度的影响，最优拉丁超立方设计方法是在设计空间获取能够反映真实模型仿真点的常用方法，在试验因素设计空间区域内进行均匀、随机、正交采样，可以较少的点获取大量的模型信息[10]。如表1所示，首先采用最优拉丁超立方设计方法选取23组样本点，对23组样本点的模型进行仿真分析，得到相应的响应值，然后构建响应面模型作为微元胞结构参数的近似分析模型，最后采用遗传算法（Genetic Algorithm，GA）获得内凹三角形微元胞的最优结构参数。

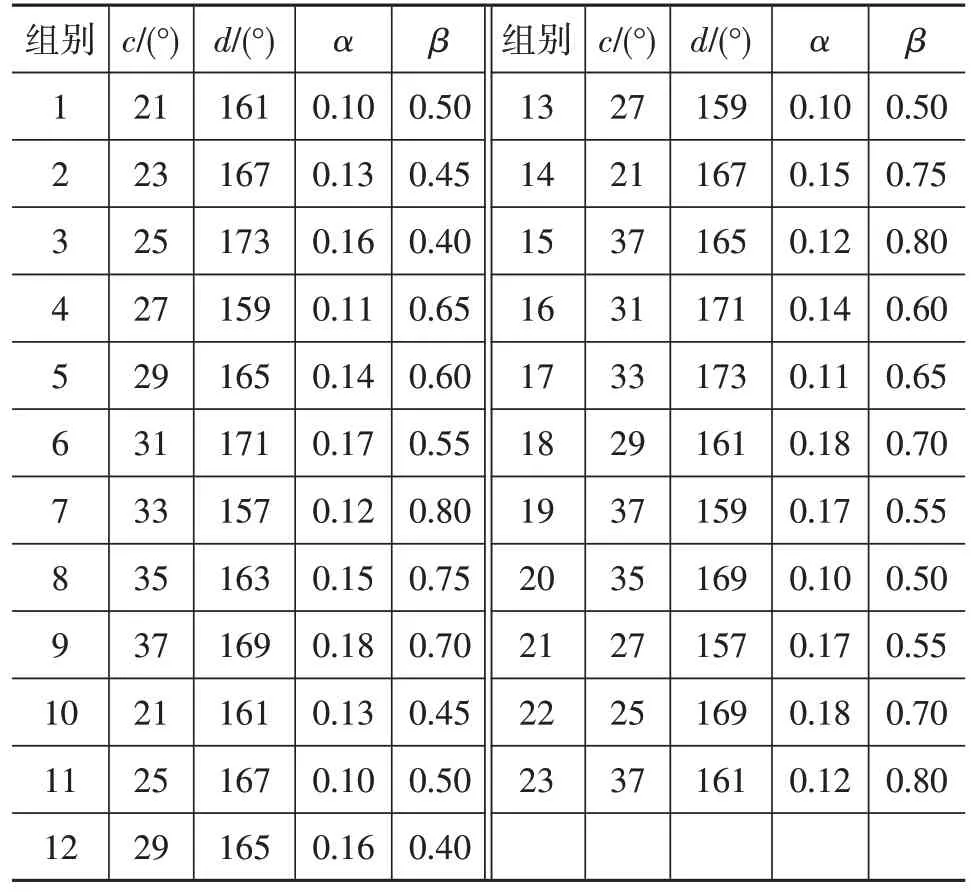
表1 不同样本点选取

内凹三角形微元胞多目标优化模型为：优化目标为SEA最大、PCF最小、相对密度最小；优化变量为α、β、c、d，边界条件设定为α∈(0,1)、β∈(0,1)、c∈(20°,40°)、d∈(140°,180°)。

基于上述样本点建立有限元仿真模型，求解获得响应值SEA和PCF。在Isight软件中采用三阶响应面模型拟合，得出代理多项式：

式中，xj(j=1,2,3,4)为样本点值；λj(j=1,2,3,…,15)为系数；y为响应值，即SEA和PCF。

SEA和PCF的表达式分别为：

式中，Fcr为峰值力。

响应面模型拟合误差分析主要通过相关数值R2展现，通常，当R2≥0.9 时满足近似拟合条件。图9 所示为(c,d)、(c,α)、(c,β)、(d,α)、(d,β)、(α,β)6 组样本点条件下微结构的SEA和PCF响应面模型。由图9可知，响应面模型均曲面光滑、斜率及其变化率均较大，可知SEA 和PCF受4个变量的影响均显著。在此基础上，响应面模型误差分析的相关参数R2为0.97，进一步说明了式（13）和式（14）的准确性与可靠性。

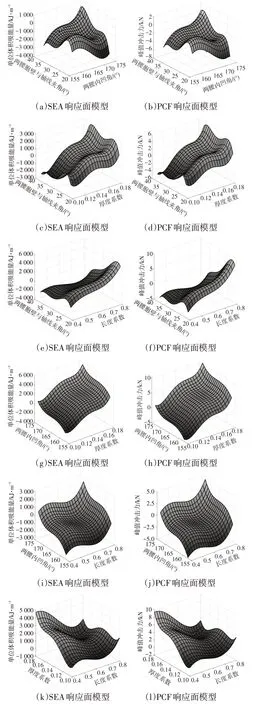
图9 各样本点条件下微结构的SEA和PCF响应面模型

基于上述SEA和PCF响应面模型，获得最优的微元胞结构参数为α=0.11、β=0.84、c=24°、d=149°，此时，峰值冲击力为332.6 N，单位体积吸能量为455.1 kJ/m3。

4 B柱材料选取及铺层方案

4.1 基体材料

聚乳酸是一种绿色材料，可应用于汽车部件[11]，椰壳纤维兼具优异的力学和热学性能，可与聚乳酸复合增强其强度与刚度特性，有效提升椰壳纤维利用率[12]。碳纤维是一种高强度、高模量的纤维材料，具有耐高温、耐腐蚀、耐疲劳等优点[13]。碳纤维密度为1 750 kg/m3，泊松比为0.307，弹性模量为210 GPa。

聚乳酸质量分数对聚乳酸椰壳纤维复合材料的冲击性能具有显著影响，如图10 所示，改变聚乳酸材料中椰壳纤维的含量可改变复合材料的强度与刚度特性。本文将聚乳酸椰壳纤维复合材料应用于B 柱夹芯微结构中，以满足B 柱高强刚度和优异吸能特性的需求。

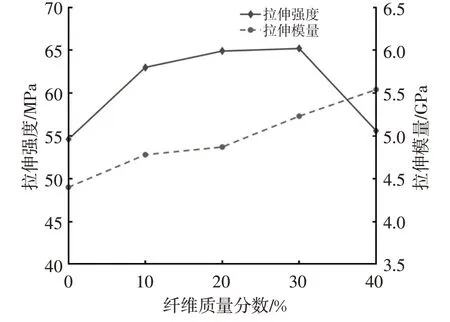
图10 不同纤维含量条件下复合材料拉伸性能

由图10 可知，椰壳纤维含量为30%处的材料拉伸强度和拉伸模量达到极大值，内凹三角形负泊松比微结构的基体材料选择椰壳纤维和聚乳酸含量比值为3∶7的复合材料[14]，主要参数如下：密度为1 189 kg/m3，泊松比为0.3，弹性模量为4.48 GPa。

4.2 B柱铺层方案

基于均衡对称铺设、铺层定向和铺设顺序的铺设原则[15]，为减少层间开裂和边缘分层现象，碳纤维铺层不宜超过4层。因此，厚度变量范围为0.1～0.5 mm[15]，选定初始铺层角度分别为45°、0°、90°和-45°，设置单层初始厚度为0.2 mm，铺层4层。

5 复合材料B柱厚度优化及对比分析

优化获得B柱夹芯结构的最佳厚度，并经联合优化获得内凹三角形负泊松比微结构最优拓扑参数，最后依据实际制造工艺选取夹芯微元胞的层数。

5.1 B柱厚度优化

构建包含B柱内板、外板以及复合材料B柱加强板的B柱总成三维有限元模型，网格大小设置为10 mm[16]。为简化计算，采用薄板代替B 柱夹芯微结构层[17]，所建立的B柱有限元模型如图11所示。

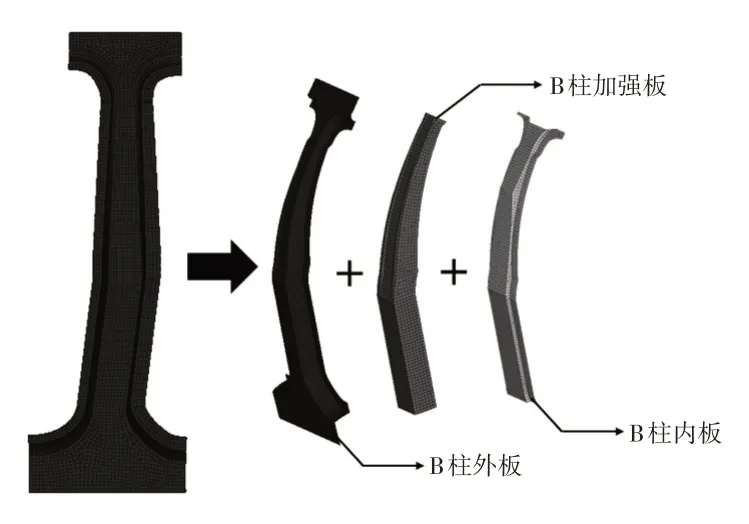
图11 B柱有限元模型

赋予薄板一初始厚度，B 柱底端和顶端自由度全约束，在B 柱中心处施加大小为1 000 N 的力，约束Y轴方向位移不超过7.163 mm[18]。本文以质量最小为目标，采用OptiStruct 求解器对B 柱进行优化设计，经过7次迭代，获得其内、外板和夹芯层的最优厚度，其中，内、外板碳纤维45°、0°、90°和-45°铺层的最优厚度分别为0.484 7 mm、0.500 0 mm、0.500 0 mm、0.140 9 mm，聚乳酸椰壳纤维夹芯层最优厚度为0.765 9 mm，如图12所示。

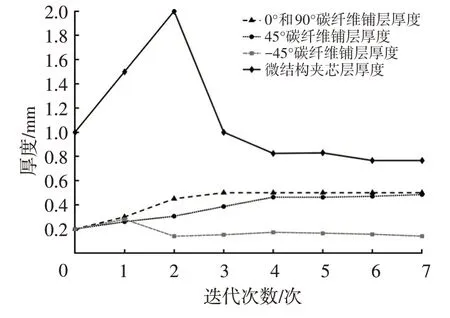
图12 碳纤维铺层和微结构夹芯层厚度优化

5.2 性能对比分析

选取侧向弯曲、后向弯曲、三点弯曲3 种典型工况[19]，将优化后的复合材料B 柱与碳纤维B 柱、无夹芯碳纤维B柱进行性能对比分析，碳纤维B柱和无夹芯碳纤维B柱厚度分别采用优化后厚度，如表2所示。

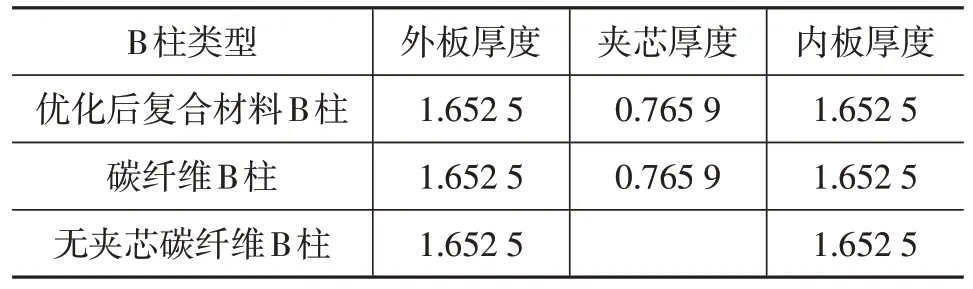
表2 3种类型B柱层厚分布 mm

5.2.1 侧向弯曲工况

将B 柱底部固支，在B 柱上部建立刚性单元，施加沿X轴负方向1 000 N 的拉伸载荷，加载点约束自由度1、5、6。自由度1、2、3 分别对应X、Y、Z方向的位移，自由度4、5、6 分别对应绕X、Y、Z轴的旋转，3 种材料B 柱的位移和应力云图如图13～图15所示。

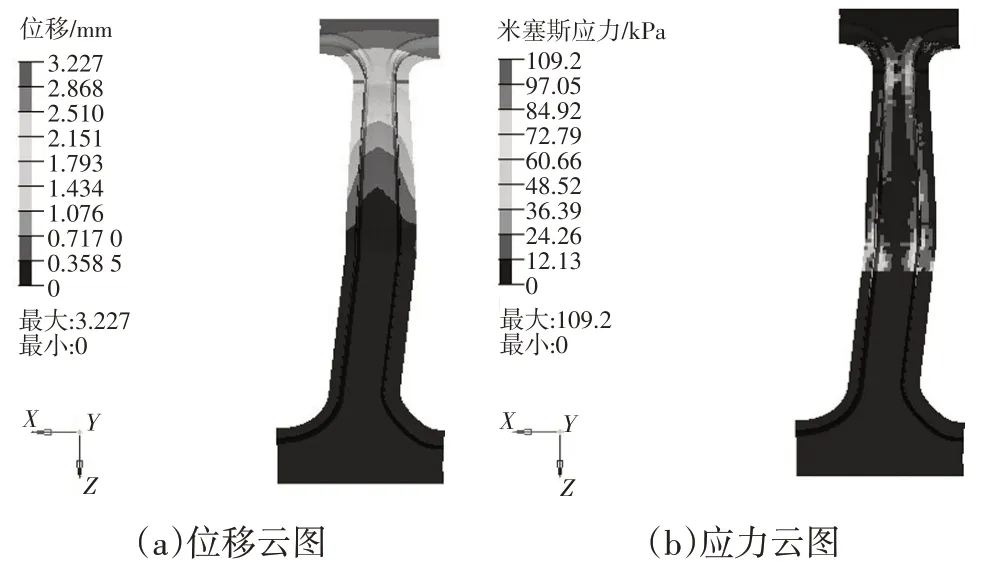
图13 侧向弯曲工况下优化后复合材料B柱的位移和应力云图

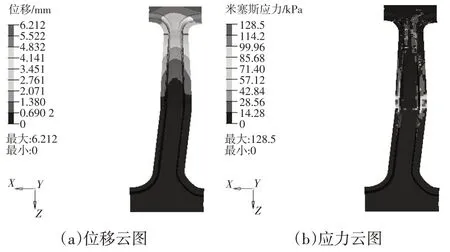
图14 侧向弯曲工况下碳纤维B柱的位移和应力云图

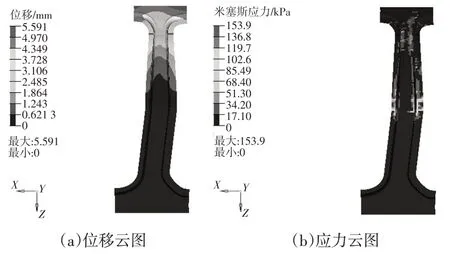
图15 侧向弯曲工况下无夹芯碳纤维B柱的位移和应力云图

5.2.2 后向弯曲工况

将B 柱底部固支，在B 柱顶部形心处建立刚性单元，沿Y轴负向施加1 000 N的拉伸载荷，加载点约束自由度2、4、6。3 种类型B 柱的位移和应力云图如图16～图18所示。

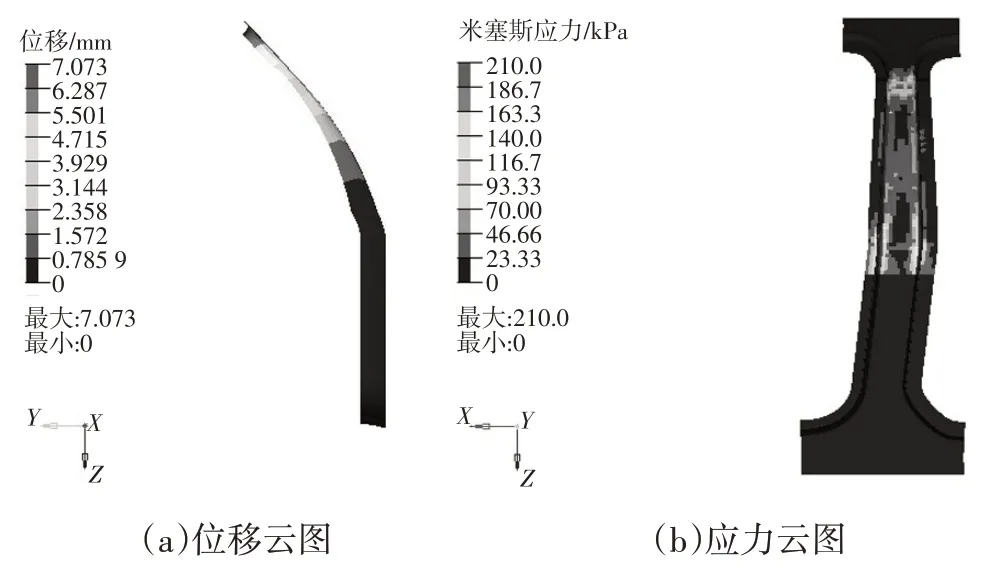
图16 后向弯曲工况下优化后复合材料B柱的位移和应力云图

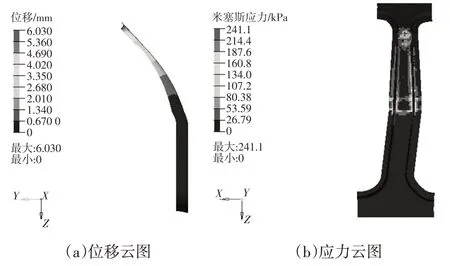
图17 后向弯曲工况下碳纤维B柱的位移和应力云图

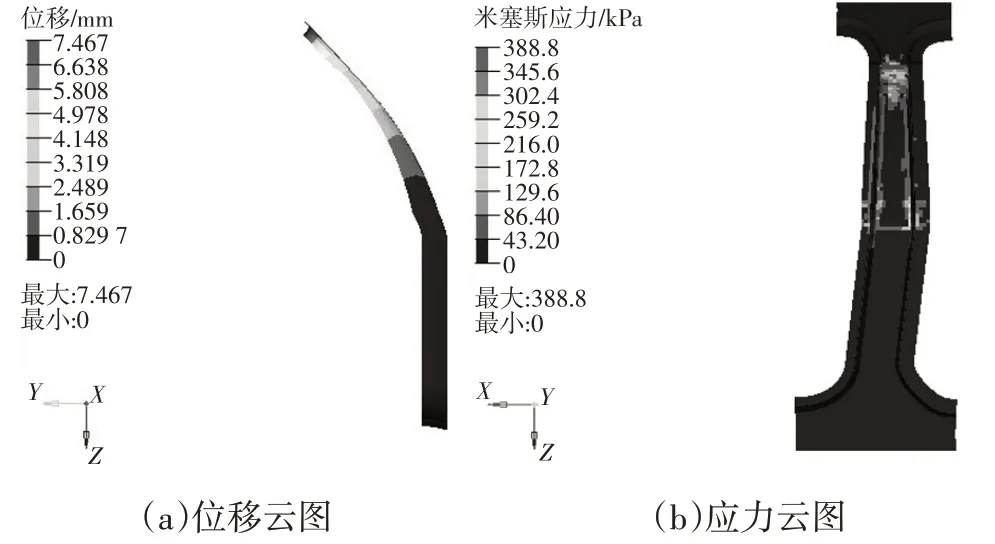
图18 后向弯曲工况下无夹芯碳纤维B柱的位移和应力云图

5.2.3 准静态三点弯曲工况

为简化分析过程，将碰撞中的圆柱刚体的动载荷转化为其与汽车B柱接触瞬间的静载荷[15]，设置刚性圆柱直径为165 mm，位置设置于B柱两端Z轴坐标中点的外表面上边缘：对B 柱下端施加1、2、3、5、6 共5 个自由度的约束，即变形过程中B柱下端仅可在X轴上可自由转动；对B柱上端施加1、2、5、6共4个自由度的约束，即变形过程中B 柱上端仅可沿Z轴滑动和绕X轴自由转动。对刚性圆柱上表面在沿Y轴负方向上均匀地施加80 mm 的强制位移，且压缩速度设为4 mm/min[20]，如图19所示。

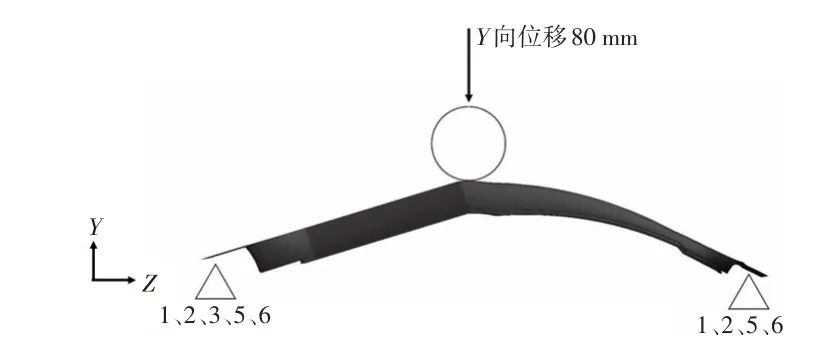
图19 三点弯曲工况仿真分析B柱边界条件及加载条件

在三点弯曲工况下，3 种类型B 柱的接触力与时间关系曲线如图20所示。由图20可知：当刚性圆柱下压距离为70 mm时，优化后复合材料B柱所受的接触力最大，为34 206.83 N；当刚性圆柱下压距离为66 mm时，碳纤维B 柱的接触力最大，为30 370.55 N；当刚性圆柱下压距离为55.3 mm时，无夹芯碳纤维B柱的接触力达到最大，为18 995.25 N。综上可知，相较于碳纤维B 柱和无夹芯碳纤维B柱，优化后复合材料B柱的最大接触力大于两者的最大接触力，即优化后复合材料B柱的强度高于碳纤维B柱和无夹芯碳纤维B柱。

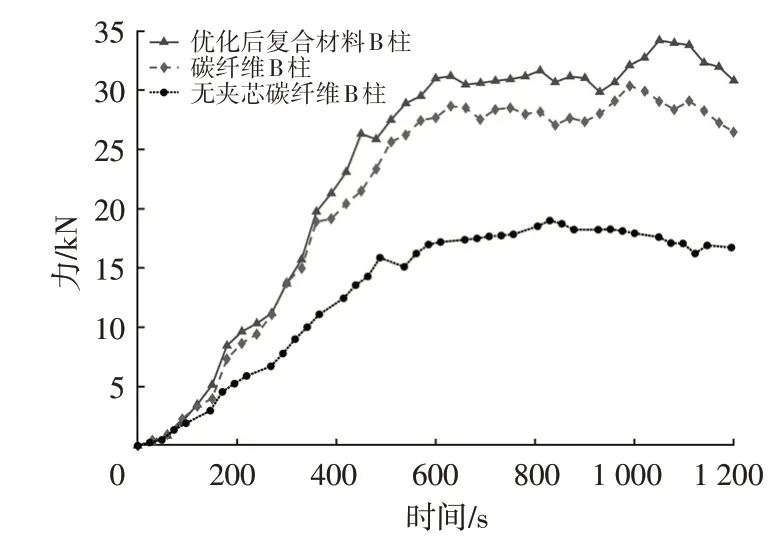
图20 三点弯曲工况下3种类型B柱接触力与时间的关系曲线

在三点弯曲工况下，优化后复合材料B 柱、碳纤维B柱和无夹芯碳纤维B柱的最大位移分别为83.25 mm、83.27 mm和85.07 mm。由此可得，优化后复合材料B柱的强度最优。

5.3 结果分析

综合以上分析结果，可得3种类型B柱在侧向弯曲和后向弯曲工况下的最大位移和最大应力及在三点弯曲工况下的最大位移和最大接触力，如表3所示。

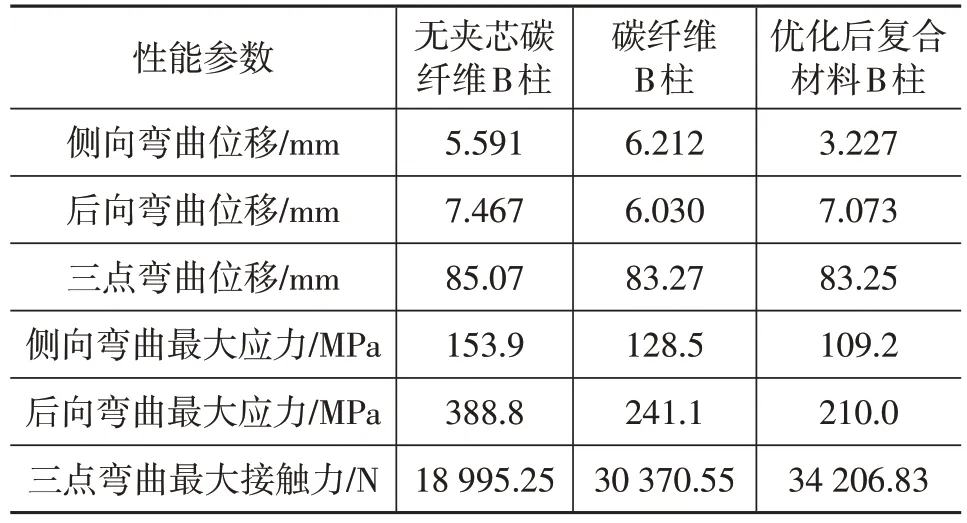
表3 3种类型B柱性能对比

由表3 可知：在侧向弯曲工况下，相较于无夹芯碳纤维B柱与碳纤维B柱，优化后复合材料B柱侧向弯曲位移和侧向弯曲最大应力均降低；在后向弯曲工况下，相较于无夹芯碳纤维B柱，优化后复合材料B柱后向弯曲位移减小，但相较于碳纤维B柱后向弯曲位移略有增大，同时相较于无夹芯碳纤维B 柱与碳纤维B 柱，优化后复合材料B柱后向弯曲最大应力降低；在三点弯曲工况下，相较于无夹芯碳纤维B 柱与碳纤维B 柱，优化后复合材料B柱三点弯曲位移减小，弯曲最大接触力有所提高。此外，相较于碳纤维B 柱，优化后复合材料B 柱质量减轻。

6 结束语

本文提出一种内凹三角形负泊松比夹芯微结构B柱，推导出内凹三角形微元胞的相对密度表达式，对微元胞结构参数进行多目标优化，得到微结构的最优微拓扑参数，对B 柱进行厚度优化设计，得到具备最优碳纤维铺层、夹层厚度和微拓扑的参数并确定其微结构层数。最后，将优化后的复合材料B柱分别与无夹芯碳纤维B柱和碳纤维B柱在侧向弯曲、后向弯曲和三点弯曲工况下进行性能对比分析，可得以下结论：

a.在侧向弯曲工况下，相较于无夹芯碳纤维B柱与碳纤维B柱，优化后复合材料B柱侧向弯曲位移分别降低42.28%和48.05%，具有优异的抵抗变形能力。

b.在后向弯曲工况下，相较于无夹芯碳纤维B 柱，优化后复合材料B柱后向弯曲位移降低5.28%。

c.在三点弯曲工况下，相较于无夹芯碳纤维B柱和碳纤维B柱，优化后复合材料B柱三点弯曲最大接触分别提升80.08%和12.63%，位移分别降低0.02%和2.14%，其强度提高。

d.相较于碳纤维B柱，优化后复合材料B柱质量减轻3.6%。

受试验条件和加工工艺等方面限制，本文缺乏对优化后复合材料B 柱的三点弯曲试验验证。后续随着先进制造工艺的发展，可制作实体样件以验证优化后结果的准确性。