基于博弈论的一体化防撞梁多目标优化设计*

李书华 吴宗扬 贝璟 余承斌 张代胜

（1.合肥工业大学，智能制造技术研究院，合肥 230051；2.合肥工业大学，汽车与交通工程学院，合肥 230009；3.合肥长安汽车有限公司，合肥 230031）

主题词：一体化防撞梁 博弈论 碰撞安全性能 纳什均衡 多目标优化

1 前言

在低速正面碰撞过程中，最先承担缓冲吸能作用，进而保证乘员安全的被动安全部件是防撞梁，国内外许多学者对其展开了广泛的研究[1]。Wang[2]等采用非支配排序遗传算法-Ⅱ（Non-dominated Sorting Genetic Algorithms-Ⅱ，NSGA-Ⅱ）和电子搜索算法（Electronic Search Algorithms，ESA）对负泊松比保险杠系统的结构参数进行寻优。贺良国等[3]运用NSGA-Ⅱ对多胞结构的车身前端结构参数进行寻优。徐峰祥[4]采用NSGA-Ⅱ对拼焊板结构进行了多目标优化设计。上述文献使用的传统优化算法在进行耐撞性多目标优化模型求解时，无法稳定地输出最优解，且未考虑不同结构参数对优化目标的不同影响，从而降低了最终方案的优化效果。

博弈论作为一种研究具有斗争或竞争性质现象的数学理论和方法，已被广泛应用于各个领域。Staňková等[5]使用博弈论方法优化了癌症的治疗。胡永进等[6]构建了多阶段网络欺骗博弈模型，为网络安全主动防御研究提供有效指导。防撞梁的耐撞性与轻量化之间的矛盾性可视为一种博弈问题，由于博弈理论中纳什均衡解具有“稳健性”和“自我强制性”的特点，使得多目标优化模型能够稳定而客观地输出最优解[7]。

综上，针对一体化防撞梁的耐撞性和轻量化设计问题，本文提出一种基于博弈论的防撞梁多目标优化方法。首先根据防撞梁的耐撞性和轻量化研究特点以及影响因素分析，将防撞梁的比吸能和质量作为博弈双方进行博弈，将防撞梁的结构参数作为博弈方的策略集，然后通过引入博弈距离和博弈力矩进行策略归属构建，最后通过对博弈方效用函数的对比分析寻找纳什均衡点，从而得到优化模型的最优解。

2 方法论

2.1 多目标优化模型与博弈模型的映射关系

从博弈论的角度思考，多目标优化设计问题与博弈决策问题有如下关联[8]：

a.将多目标优化模型视为博弈模型。

b.设计变量X及其取值范围对应博弈决策问题的策略集C及其可行空间，可通过一定方法将设计变量X拆分为策略集C1,C2,…,Cq。

c.将优化目标视为博弈决策问题的博弈方，将优化算法视为纳什均衡分析。

d.多目标优化设计问题的目标函数的响应值等同于博弈决策问题中博弈方所获得的效用，且两者的约束也可视为一致。

故可用博弈决策问题的思维方式来描述多目标优化设计问题：

式中，G为多目标优化模型空间集合；V1,V2,…,Vq为q个博弈方；C1={xi,…,xj},…,Cq={xk,…,xl}为q个博弈方的策略集，并满足C1∪C2∪…∪Cq=X且Ca∩Cb=0；a,b=1,2,…,q且a≠b。

2.2 优化流程

对防撞梁进行多目标优化设计的目的在于获得耐撞性和轻量化函数的最优解。优化过程主要分为3 个阶段，即策略归属构建、效用函数构建和纳什均衡分析，优化流程如图1所示。

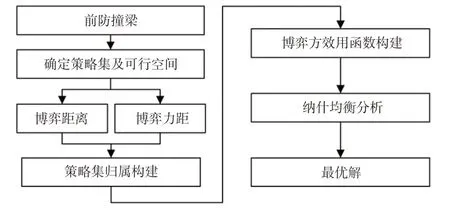
图1 防撞梁的博弈优化设计流程

2.2.1 策略归属构建与博弈效用函数构建

博弈方的策略集归属构建是多目标优化设计问题转为博弈决策问题的关键。为此，引入博弈距离和博弈力矩的概念[9-10]：

a.博弈距离。博弈距离定义为项目i到博弈方v的距离与所有项目到与其对应的各博弈方距离之和的比，其中，项目i到博弈方v的距离表示为uv,i的倒数：

式中，∀i∈[1,…,n]；∀v∈[1,…,q]；uv,i为项目对i博弈方v的效用；n为博弈方的数量；dv,i为项目i到博弈方v相对于其他博弈方的博弈距离。

b.博弈力矩：

式中，φv,i为项目i到博弈方v相对于其他博弈方的博弈力矩。

策略集归属构建步骤如下：

a.通过粒子群算法对各目标函数进行单目标优化，得到初始效用和初始策略集。

b.按照式（2）和式（3）计算博弈距离和博弈力矩，对于某一个博弈方vw，将各项目到博弈方vw的博弈距离按照升序排列，表示其优先级顺序从高到低，并按照博弈距离排列顺序计算相对应的累加博弈力矩。

同时，为了简化优化过程，从而提高优化效率，需要将模型仿真替换为数值优化，因此，博弈效用函数的构建是必不可少的。

2.2.2 纳什均衡分析

设X={x1,x2,…,xq}=C={C1,C2,…,Cq}为博弈方的策略集，V1(c),V2(c),…,Vq(c)为博弈所获得的效用，博弈流程如下：

a.基于博弈距离和博弈力矩，得到隶属于各博弈方的策略集{C1,C2,…,Cq}。

3 有限元模型建立与可行性检验

3.1 正面碰撞有限元模型建立

汽车前防撞梁能在低速碰撞中起到吸能和缓冲的作用[11]。本文采用台车正面碰撞有限元模型对防撞梁的低速正面碰撞性能进行仿真，如图2 所示，台车模型质量为1 530 kg，台车以1.111 m/s的初始速度撞向刚性墙，整个碰撞过程时间设定为0.06 s。该一体化精密铸造防撞梁的材料选用ZL205A 铝合金，其密度为2.82×103kg/m3，弹性模量为7.3×104MPa，泊松比为0.32。考虑应变速率对材料应力-应变曲线的影响，材料类型选择MAT24。

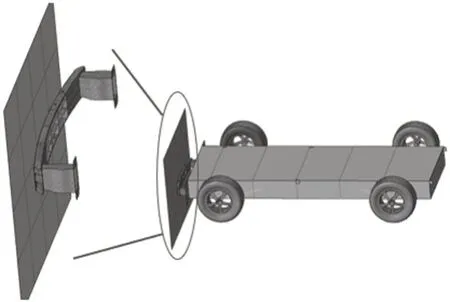
图2 台车正碰有限元模型

3.2 有限元模型可行性检验

能量守恒是判断正面碰撞有限元模型是否可靠的重要标准。简化积分方法往往会导致沙漏模式，从而损失部分能量，影响系统的仿真精度[12]。一般要求质量增加不超过5%，总能量增加不超过10%，产生的沙漏能不超过总能量的5%，且不为负值。针对防撞梁低速正碰仿真模型，碰撞过程中的能量变化如图3所示，从图3中可以看出，总能量处于平稳状态，沙漏能几乎为零，能量始终守恒，故碰撞模型合理，可用于后续优化设计。

图3 能量变化曲线

4 防撞梁博弈优化

4.1 初始设计分析

防撞梁的耐撞性评价指标可以用比吸能、峰值碰撞力和吸能量来衡量。此外，为了保证乘员具有充足的生存空间，防撞梁在碰撞过程中的最大纵向位移也不应超过许可值[13]。一体化精密铸造防撞梁的初始效用如表1所示，由于最大纵向位移和峰值碰撞力的矛盾性，从表1 中可以看出，最大纵向位移的安全设计余量较大，而峰值碰撞力过大，存在一定安全隐患。为了进一步增强防撞梁的碰撞安全性能，需对其进行轻量化和耐撞性优化设计。

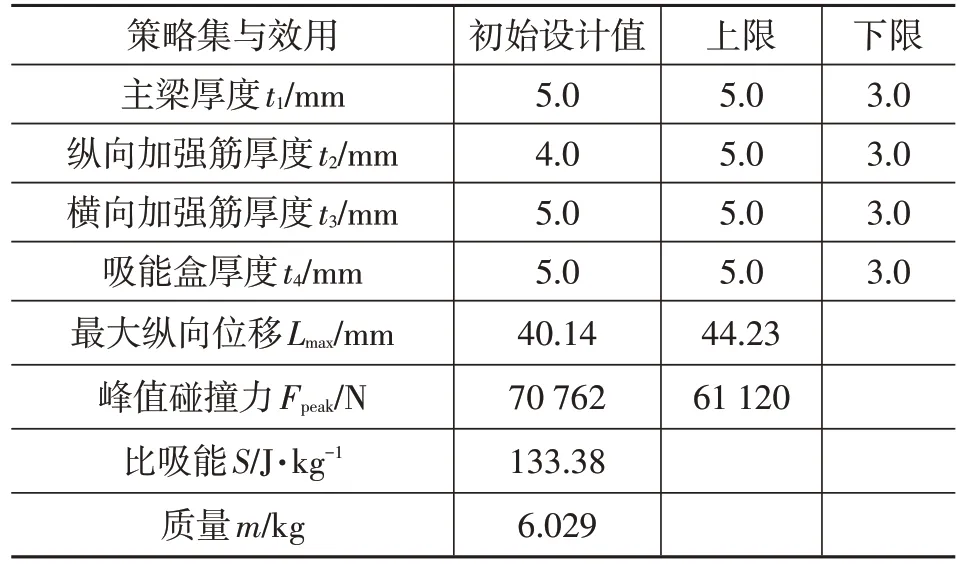
表1 设计变量及响应的初始效用

4.2 策略分析

如图4所示，本文选取防撞梁的主梁、纵向加强筋、横向加强筋和吸能盒的厚度（t1～t4）为策略集，并以峰值碰撞力Fpeak和最大纵向位移Lmax为约束条件，以防撞梁的比吸能S和质量m为博弈方，比吸能和质量的响应值为博弈方所获得的效用。

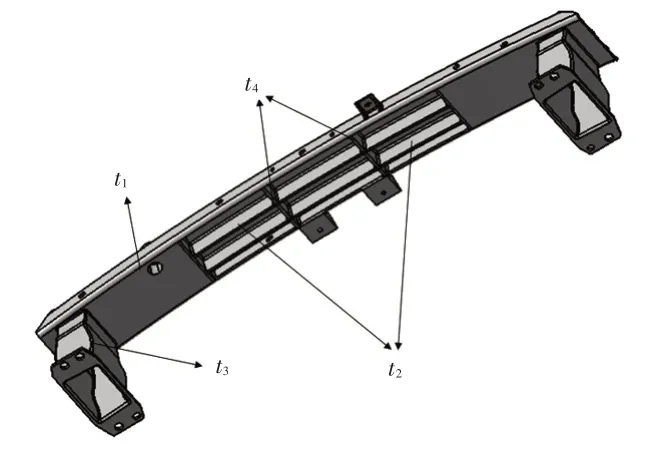
图4 防撞梁的厚度变量

按照策略集划分步骤，首先对防撞梁的比吸能和质量分别采用粒子群单目标优化算法（种群大小为100，迭代次数为30，惯性权重因子为0.9，学习因子c1和c2取0.9），得到初始效用和初始策略集。根据式（2）和式（3）分别计算各博弈方的博弈距离和博弈力矩，如表2 所示。

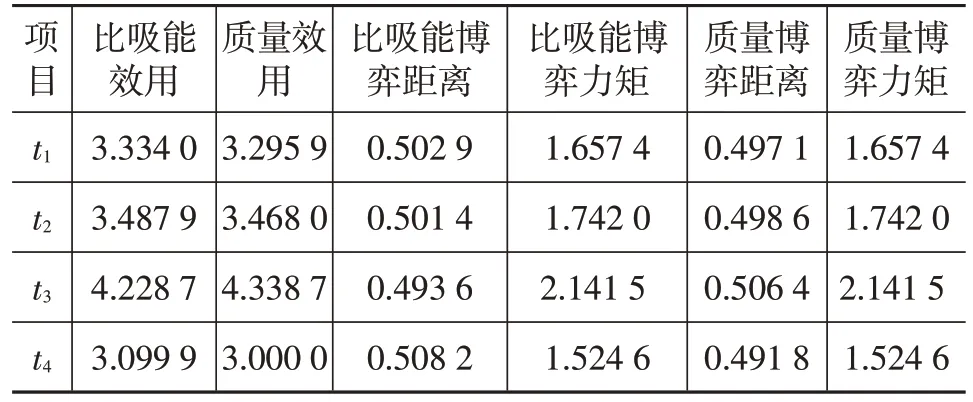
表2 各项目的效用、博弈距离和博弈力矩

根据表2中比吸能的博弈距离进行升序排列，并根据博弈力矩φs,ti计算相对应的累加博弈力矩ai，如表3所示。计算可得平衡值uv=3.532 8，通过比较平衡值uv和各项累加博弈力矩来确定属于博弈方比吸能的策略集，即C1=(t2,t3)，其他的项目为博弈方质量的策略集，即C2=(t1,t4)。

表3 各项目的累加博弈力矩

4.3 博弈效用函数构建

博弈效用函数采用响应面法构建，它能通过试验设计所得到的样本数据来探测输入变量与输出响应之间的敏感度，最终将其拟合成函数关系，从而把结构优化问题转化为数值优化问题，大幅提高优化效率。

试验设计方法的选择对构建高精度的效用函数很重要。本文采用最优拉丁超立方试验设计方法构建响应面模型，它能将试验设计点均匀地分散在设计空间中，具有很好的空间填充性和均衡性[14]。采用30个采样点来构建防撞梁峰值碰撞力、最大纵向位移、比吸能和质量的二次响应面近似模型，并且通过不断增加试验设计点来更新近似模型，直到近似模型的精度满足要求。本文主要采用确定系数R2对响应值进行精度评价，Lmax、Fpeak、S、m的确定系数分别为0.999、0.927、0.999、0.999，均满足要求，说明所构建的效用函数是可靠的。

4.4 结果与讨论

4.4.1 纳什均衡分析

随机确定初始策略集，基于纳什均衡分析，博弈方的比吸能和质量的迭代过程如图5所示，从图5中可以看出，在第10次迭代时，质量最小，比吸能达到最大，满足收敛准则。经过协调权衡，峰值碰撞力与最大纵向位移均在安全范围内。

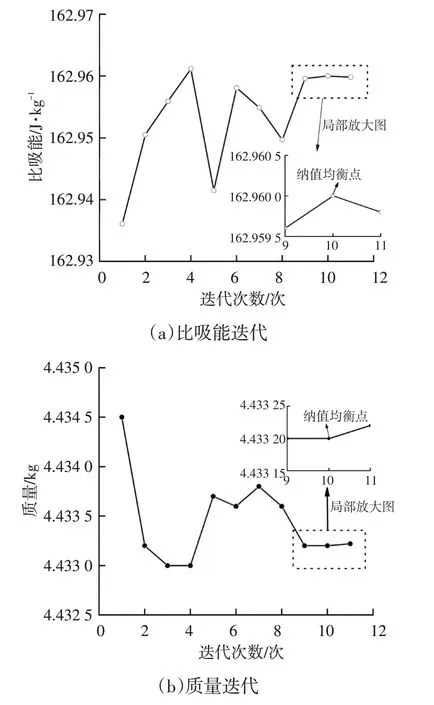
图5 博弈方迭代过程

4.4.2 各类优化算法对比分析

采用粒子群多目标优化算法、多岛遗传算法以及非支配解排序遗传算法分别对防撞梁数学模型进行求解，其中，各类优化算法相关参数设置如表4 所示，优化结果如表5所示。从表5中可以看出：传统优化算法相比于博弈优化设计，比吸能均偏小，而质量均偏大；且博弈法是一种带有竞争性质的纯策略型方法，博弈双方存在“互利”解，只需较少的迭代次数便能找到纳什均衡点，求解稳定且速度快；对比初始设计，经博弈设计的防撞梁的质量减轻了26.47%。初始设计与博弈设计的防撞梁比吸能变化过程如图6所示，由图6可知，比吸能增长了22.18%，博弈设计提高了防撞梁的碰撞安全性能。

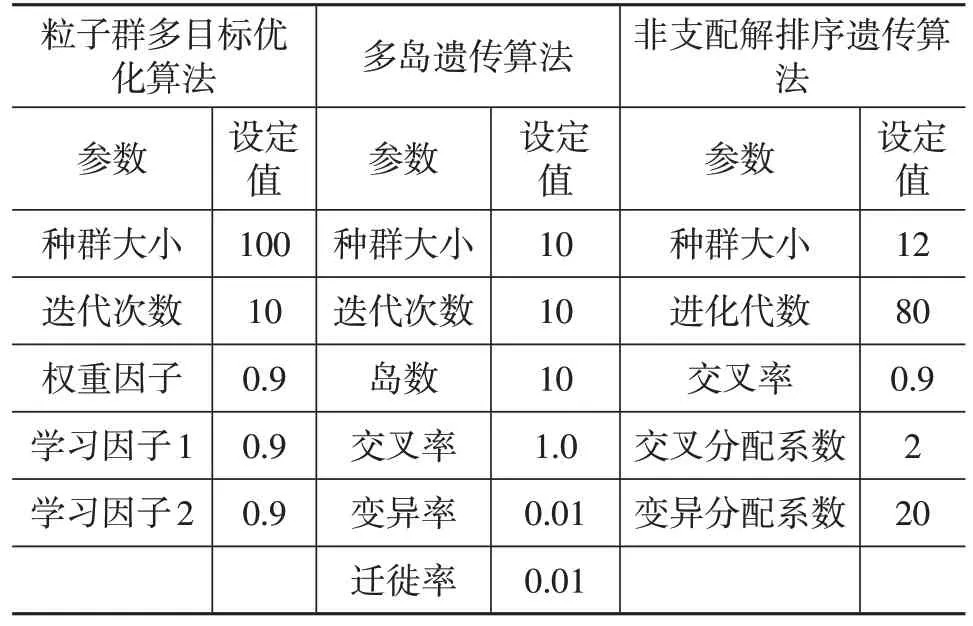
表4 优化算法参数设置

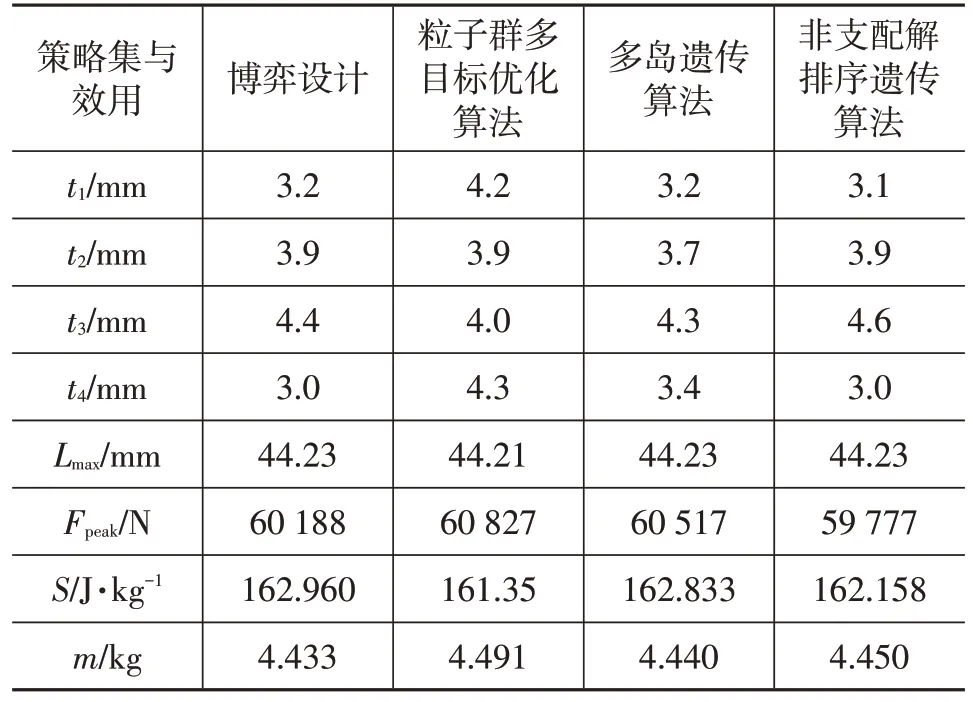
表5 优化结果对比

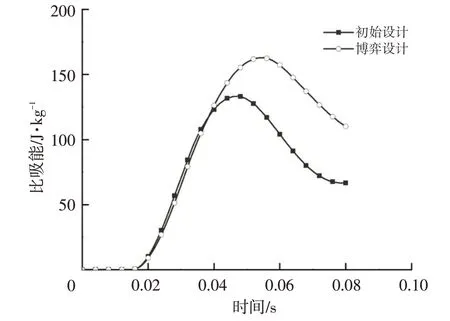
图6 初始设计与博弈设计的比吸能对比

5 结束语

本文采用“材料-结构-性能”一体化集成设计方法，能够对防撞梁进行有效优化，在保证良好的整体性能的情况下，实现防撞梁的轻量化设计。针对一体化防撞梁的耐撞性和轻量化设计特点，以比吸能和质量为博弈双方，提出了一种基于博弈论的防撞梁多目标优化方法。同时，将防撞梁多目标优化模型与非合作博弈模型进行映射，结合博弈模型的特点，基于博弈距离和博弈力矩对结构参数进行策略归属构建。

通过对效用函数的纳什均衡分析，经过10 次迭代达到收敛准则，避免了最大纵向位移安全系数设计过大的缺陷。结果表明：博弈设计的防撞梁的峰值碰撞力与最大纵向位移均在许可范围内，且相比于初始设计，防撞梁质量减轻了26.47%，比吸能增加了22.18%，相比于传统多目标优化算法，博弈设计具有更好的稳定性和优化效果，证明了其实用性与有效性。