基于高维SIFT改进隐马尔可夫模型的多目标跟踪

刘艺博， 奚峥皓， 陈健超

(上海工程技术大学 电子电气工程学院, 上海 201620)

0 引 言

自然场景下的多目标跟踪(Multi-object tracking, MOT)是计算机视觉的一个重要问题，其在自动驾驶、军事安全等领域都有广泛的应用。多目标跟踪的目的是在一个视频中根据初始帧一些标定了身份信息的目标，在后续帧中维持这些目标的身份，并形成有效的轨迹[1-2]。然而，在复杂的环境背景下，目标在运动过程中容易被环境障碍物遮挡，并且，当多个目标相互交错时容易引起跟踪目标身份的丢失和互换，导致无法从视频中提取到完整的运动轨迹。

马尔可夫模型在多目标跟踪任务中有显著的优点，为了解决MOT中的遮挡问题， Liu等[3]提出了一种轨迹耦合关联的马尔可夫随机场模型，通过整合密集人群的位置和运动信息，对其中不完整和偏差的位置数据进行校正，提高了跟踪器的精度；Xiang等[4]将MOT表述为马尔可夫决策过程中的决策，以策略学习的方式加强不同帧目标之间的数据关联；Wu等[5]将马尔可夫决策过程与不同频率的相关滤波器关联，解决了跟踪过程中因为遮挡和尺度变换造成的目标漂移问题；Vojir等[6]利用隐马尔可夫模型 (Hidden Markov Model, HMM)建立了一种HMMTxD方法的跟踪器，将检测结果作为观测值输入到模型中，并输出估计跟踪的结果，对遮挡问题有较好的鲁棒性，然而此时模型受观测状态的影响较大，状态值的选取直接影响了跟踪结果的好坏。

基于马尔可夫在跟踪任务中的优越性，针对HMM状态选取的问题，本文以SIFT算子作为模型中的状态，建立一种基于SIFT的隐马尔可夫模型(SIFT-HMM)，并将其应用到多目标跟踪任务中。针对状态关联问题，利用HMM设计一种匹配SIFT隐性、观测两种状态的方法，从而实现对遮挡目标的状态估计。针对马尔可夫模型复杂度较高的问题，利用SIFT关键点设计了一种高维的观测方法，从而增强模型的推理速度。实验结果表明，本文的跟踪器在MOT17，MOT20、KITTI公共数据集上实现较好的跟踪性能，高维模型能提高算法的推理速度。

1 基于SIFT-HMM的多目标跟踪器

通过HMM实现多目标跟踪的过程被描述为根据当前帧的目标状态，获取下一帧目标发生概率最大的状态。本文提出了一种以SIFT关键点为状态，建立HMM跟踪器模型，通过对状态值进行实时预测实现对多目标的跟踪，SIFT-HMM跟踪器的工作流程如图1所示。

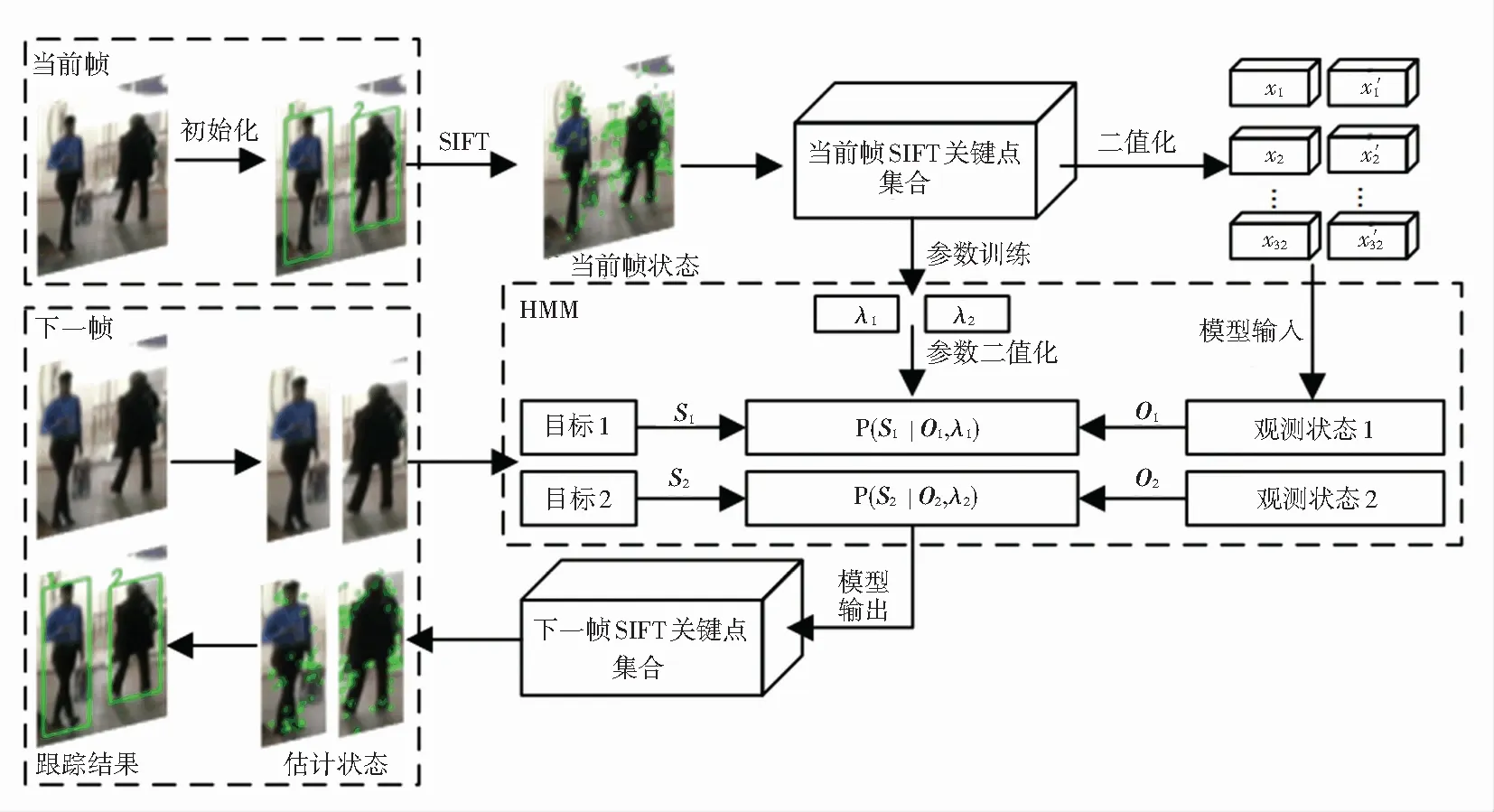
图1 基于SIFT-HMM的跟踪器工作流程

1.1 基于SIFT算法的特征关键点提取

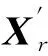
(1)

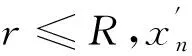
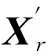
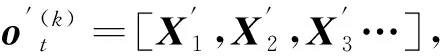
定义Ω,Ψ两个集合如式(2)所示：

(2)

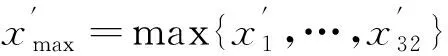
(3)

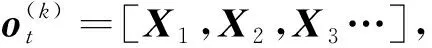
1.2 基于SIFT关键点建立的HMM

HMM由观测状态序列O、隐性状态序列S和参数λ组成。观测状态是实时状态可以观测的，用SIFT提取的关键点集表示观测状态，可得在t帧时的SIFT关键点集合为ot，那么由T帧序列组成的视频的观测序列为O={o1,o2,o3,…,oT}。隐性状态是不可被直接观测的未知状态，用t+1帧的估计SIFT关键点集表示t帧的隐性状态，那么由T帧序列组成的视频的隐性状态序列为S={s1,s2,s3,…,sT}，HMM中模型单帧的状态转移结构，如图2所示。

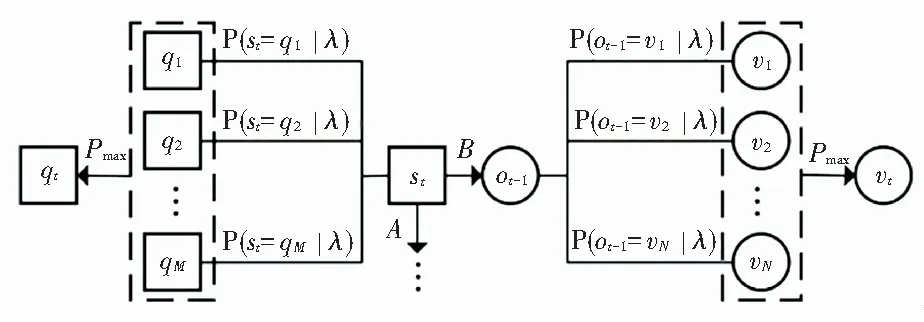
图2 HMM中单帧状态转移的结构图

此外，视频首帧图像的隐性状态与观测状态都表现为检测器检测得到的初始化结果，此时s1不具有实际意义，在数值上s1取值与o1一致；而视频在最后一帧的图像是跟踪器的终止帧，模型在最后一帧时的观测状态oT不具有实际意义，在数值上取值与sT一致，故模型实际输入的两个状态序列为O={o1,o2,…,oT-1}和S={s2,s3,…,sT}。

跟踪器工作时，当前帧的目标状态是由上一帧的状态决定的，即t帧目标的状态st与t-1帧时的观测状态ot-1有关，当t∈[2,T]，用Ft表示第t帧时模型的状态向量,如式(4)所示：

Ft=[ot-1,st,λ]

(4)

其中，模型的参数λ=(A,B,Π)，分别表示状态转移概率矩阵、观测概率矩阵和状态概率向量。

t帧状态ot-1所能取到的观测状态数量是有限的，此时的状态数量为N(N∈Z+)，由于ot-1与st存在矩阵变换关系，故隐性状态st所能取到的状态数量也是有限的，隐性状态数量为M(M∈Z+)。用V={v1,v2,…,vN}表示所有的观测状态集合，Q={q1,q2,…,qM}表示所有的隐性状态集合，则P(|ot-1|=vt)表示观测状态ot-1取到vt的概率，如式(5)所示，P(|st|=qt)表示t帧时隐性状态st取到qt的概率，如式(6)所示：

P(|ot-1|=vt)=max{P(|ot-1|=v1),…,P(|ot-1|=vN)}

(5)

P(|st|=qt)=max{P(|st|=q1),…,P(|st|=qM)}

(6)

其中，vt∈V，qt∈Q。

状态在相邻帧之间的转移是通过参数λ的变换关系来传递的，且参数包含3个子参数，即λ=(A,B,Π)分别表示状态转移概率矩阵，观测概率矩阵，状态概率向量，如式(7)～式(9)所示：

(7)

(8)

Π=[π1,π2,…,πM]1×M

(9)

其中，aij表示t-1帧的状态qi转移到t帧的状态qj的概率，aij=P(|st|=qj||st-1|=qi)；bij表示t帧隐性状态qi产生观测值vj的概率，bij=P(|ot-1|=vj||st|=qi)；πi表示初始帧的状态qi出现的概率；πi=P(|s1|=qi)，下角标i,j表示可能状态的标号。

确定每一帧状态的取值以及帧与帧之间传递关系后，HMM可以用O,S,λ之间的关系来表示，如式(10)所示：

P(O,S|λ)=P(F1,F2,…,FT)=P(F2,…,FT-1,oT,s1|λ)=P(o1,…,oT-1,s2,…,sT,oT,s1|λ)=πs1bs1o1as1s2bs2o2…ast-1stbstot

(10)

1.3 SIFT-HMM的高维观测状态

1.3.1 高维观测状态的描述

基于HMM建立的多目标跟踪器一般对每个目标建立独立的HMM，状态表示为每个目标的全部关键点集，此时的观测维度较低，将其定义为初始的低维状态模型。

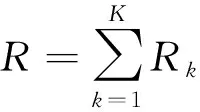
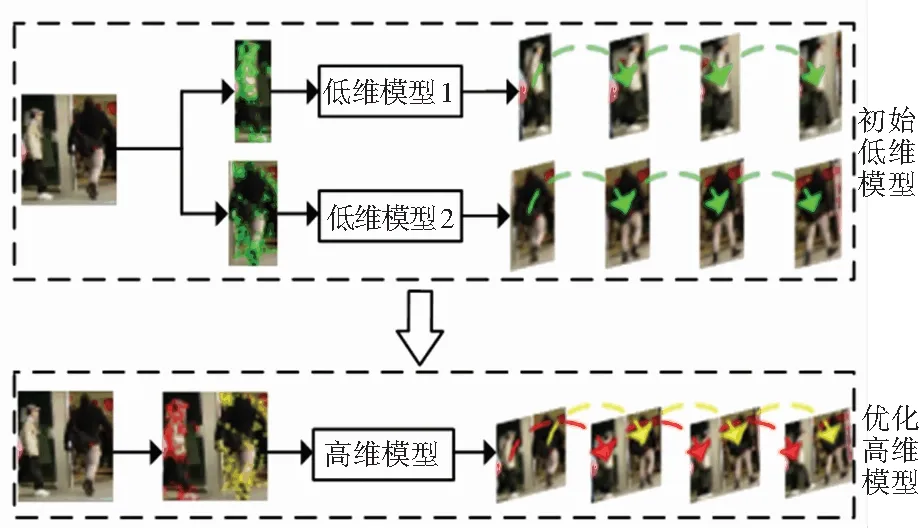
图3 优化高维模型的原理图

高维模型中，ot表示t帧K个目标的观测状态，包含目标数量、关键点数量、关键点维度3重信息。t帧时模型的状态向量Ft包含K个目标和R个关键点，每个关键点在形式上表现为一个m×n的二维矩阵，那么ot在形式上表示为一个K×R×m×n的四维数组，将高维数组ot进行逐层分解，则有式(11)：

ot=[ot(1),ot(2),ot(3),…,ot(K)]

(11)

其中，ot(k)表示t帧时第k个目标的观测值，表现为R×m×n的三维数组，如式(12)所示：

ot(k)=[ot(k)|1,ot(k)|2,ot(k)|3,…,ot(k)|R]T

(12)

其中，ot(k)|r表示t帧时第k个目标在第r个关键点的观测值，表现为m×n的二维矩阵，如式(13)所示：

(13)

关键点由1×32的描述子向量表示，即m×n=1×32，故ot(k)|r可改写为式(14)：

ot(k)|r=[x1(t),x2(t),…,x32(t)]

(14)

根据式(11)～式(14)，t帧时K×R×m×n的观测状态ot表示为K×R×n(n=32)的三维数组，如式(15)所示：

(15)

1.3.2 高维观测状态模型的复杂度

低维状态模型和高维状态模型表现在状态维度的不同，而状态维度决定了参数的计算量，从而影响跟踪过程的推理速度。低维状态模型中每帧的状态模型针对一个目标，多个目标的场景需要多个模型同时运行，其参数总计算量等于每个模型对应参数的乘积，用μlow表示模型的复杂度，如式(16)所示：

(16)

其中，αk(t)表示第k个目标在t帧的复杂度。

高维状态模型中，每帧的状态模型针对其全部目标，多个目标的场景只需要一个模型运行，其参数计算量等于该模型的参数计算量，用μhigh表示此时模型的复杂度如式(17)所示：

(17)

低维模型的复杂度μlow表现为多个目标复杂度的积，高维模型复杂度μhigh表现为多个目标复杂度的和，则μhigh≤μlow，表明高维状态模型能一定程度的降低模型的复杂度。

1.4 SIFT-HMM的参数训练和求解

Baum-Welch方法是HMM参数学习的通用方法之一，使用该方法对SIFT-HMM的参数训练[8]。若视频序列中一共存在K个目标，初始帧图像中有k1个目标，对这k1个目标建立高维观测状态模型。该模型单独训练，得到高维模型的参数。而对于在后续帧中出现的K-k1个目标，初始化每个目标并建立低维观测状态模型，得到独立的K-k1个模型并进行训练。综合上述，1个高维模型和K-k1个低维模型，最终能够得到整个SIFT-HMM的K-k1+1个收敛的参数。对于第θ个模型，θ∈[1,K-k1+1]，该模型收敛的参数λη(θ)可由式(18)得到：

maxAη(θ)=

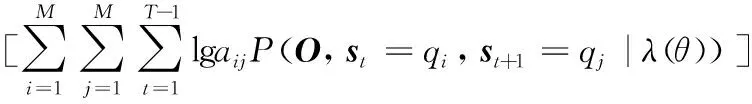
(18)

其中，Aη(θ),Bη(θ),Πη(θ)表示收敛的3个参数；maxAη(θ),maxBη(θ),maxΠη(θ)表示3个参数的极大值；η表示模型的最大迭代次数。

将式(18)得到的3个参数以及输入观测序列O代入到式(10)的计算关系式中可以得到隐性状态st的最大概率状态值如式(19)所示：

(19)

该概率最大的状态即是t帧时st的状态，逐帧计算全部T帧的状态，从而得到整个视频的状态序列S，将这些估计的状态(SIFT关键点集)用一个可视的回归框框选出来，形成关于时序t的跟踪轨迹，即得到SIFT-HMM的跟踪可视化结果。

2 基于检测器的初始化预处理方法

SIFT-HMM跟踪算法是根据初始帧选定的目标框，实现对后续帧中目标的跟踪。在建立跟踪器之前，需要对图片序列进行预处理，得到初始化结果。本文的预处理即建立一个检测器，得到图片序列的初始化目标框。选用MOT Challenge的DPM公共检测器作为检测框架，在输入到跟踪器模型前用该检测器进行目标的初始化定位，DPM检测器在MOT17-10-DPM序列的首帧检测结果如图4所示。检测器利用回归框来框选检测到的目标，而在得到待测目标的同时，图4(a)中出现了许多错检的回归框，这些错检的回归框在验证跟踪器效果时不具有实际意义，因此将第一帧图像中错检的回归框剔除，剔除异常后的检测结果如图4(b)所示，优化后的检测结果将作为跟踪器首帧的输入。

(a) DPM检测器检测结果 (b) 剔除异常后的检测结果

3 实验结果分析与算法评估

在MOT17、MOT20和KITTI公共数据集上对SIFT-HMM的性能进行评估，并与其他先进的跟踪算法进行比较分析。实验环境为一台具有Intel Corei5-9600KF CPU处理器和16 GB内存的个人电脑，算法是通过python3.8在64位Windows10操作系统上实现的。

3.1 数据集和评价指标

3.1.1 数据集

选取了3个数据集中具有各自特点的视频序列来检验跟踪器的有效性。MOT17数据集是摄像机在室外环境下拍摄到的行人视频，选取MOT17-08-DPM视频序列用于检验在拥挤、遮挡环境下的跟踪性能；选取MOT17-10-DPM视频序列用于检验在动态场景下的跟踪性能；MOT20数据集中目标数量较多，选取MOT20-01、MOT20-02数据集用于检验高维模型的优越性；KITTI数据集是针对自动驾驶的数据集，选取KITTI-0006用于检验以刚体为目标的跟踪性能。

3.1.2 评价指标

为了量化跟踪器结果，并且统一与其他对比算法的评价标准，采用IDS、MOTA、MOTP3个指标来量化多目标跟踪器的性能。其中，IDS表示在一条跟踪轨迹跟踪的过程中，目标身份发生交换的次数；MOTA表示多目标跟踪的准确率，如式(20)所示；MOTP表示多目标跟踪的精度，反应了预测结果与标准框的匹配度，如式(21)所示：

(20)

(21)

其中，FN、FP、GT表示跟踪中漏检的目标数、错检的目标数、全部目标的实际总数；dt,i表示第t帧中第i个目标对的距离；ct表示t帧中预测轨迹与GT匹配上的数目。

3.2 实验结果分析

3.2.1 可视化结果分析

SIFT-HMM在部分数据集的可视化结果如图5 所示。可视化结果表明，在3种不同的场景下，SIFT-HMM跟踪器都能对目标实现有效的跟踪。

图5 SIFT-HMM在部分数据集的可视化结果

3.2.2 优化的高维状态模型结果分析

SIFT-HMM在MOT20-02第25帧的跟踪可视化结果如图6所示，该图中目标较多，对初始帧每个目标建立独立的HMM会导致此时的跟踪器复杂度较高。

图6 MOT20-02第25帧的跟踪可视化结果

为了验证本文提出的优化高维模型的优越性，控制两个变量来设置消融实验，进而比较优化前的初始低维模型和优化后的高维观测模型的复杂度。在同一序列下截取一段视频，比较在相同视频下两个模型的运行时间，量化运行时间的指标为HZ，表示跟踪器在一秒中处理帧数的速度；保持其他条件不变的情况下，增加截取视频的帧数，比较在增加帧数之后运行时间的变化。

共选取了3个视频，分别从每个视频初始帧截取30帧的视频段和120帧的视频段做两次测试，测试的结果见表1。实验结果表明，基于高维模型的SIFT-HMM跟踪器在6个测试的HZ上都表现最优。在MOT20-01数据集的两次测试中，基于高维模型的跟踪器分别比初始模型在运行速度上提升94.11%和68.75%；在MOT20-02数据集的两次测试中，基于高维模型的跟踪器分别比初始模型在运行速度上提升183.33%和126.92%；在MOT17-08-DPM数据集的两次测试中，基于高维模型的跟踪器分别比初始模型在运行速度上提升19.28%和4.51%。这些结果表明，高维优化模型能够有效的降低跟踪器的复杂度，提升跟踪器的推理速度。

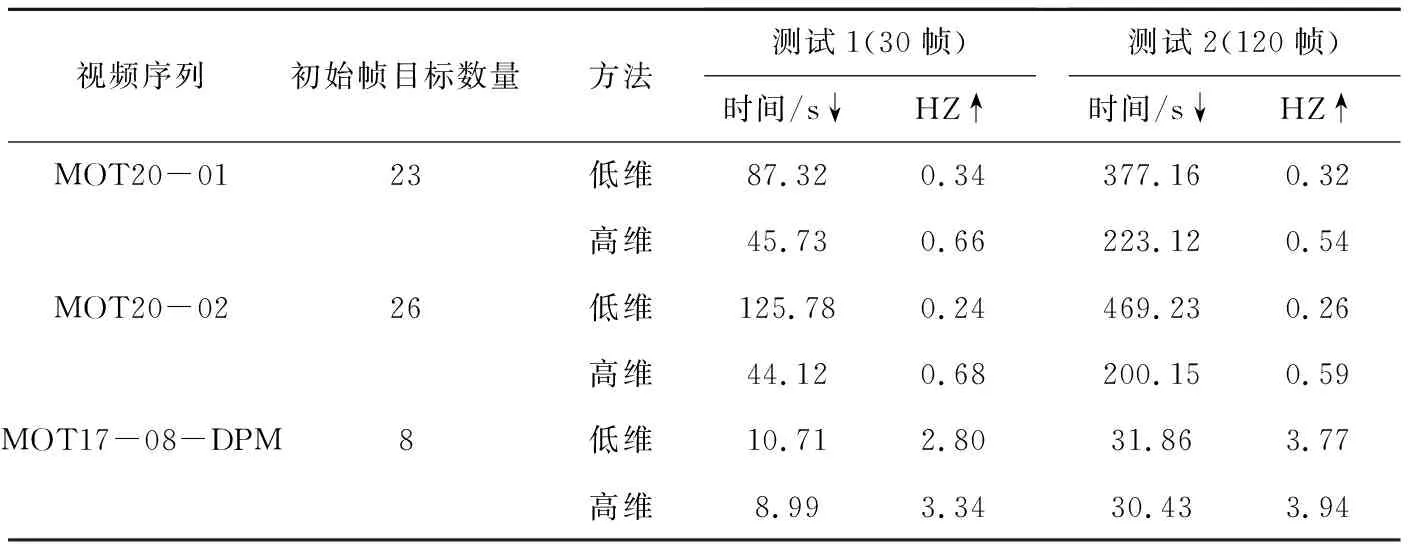
表1 SIFT-HMM高维模型与初始低维模型的消融实验

3.3 与其他跟踪算法的对比分析

为了验证SIFT-HMM跟踪器的优越性，本文选择与MOT-MDP[4]，MDP-OF[9]，HMOT[10]，JDMOT[11]跟踪算法进行对比分析，对比结果见表2。实验结果表明，对于IDS指标，本文在这3个视频序列上都取得最好的性能，比第二好的跟踪器在MOT数据集上高出33.3%～70.5%；在KITTI数据集上高出6.7%。这是由于本算法为每个目标建立的HMM，使每个目标的转移通过独立的马尔可夫链来传递，具有较好的独立性。

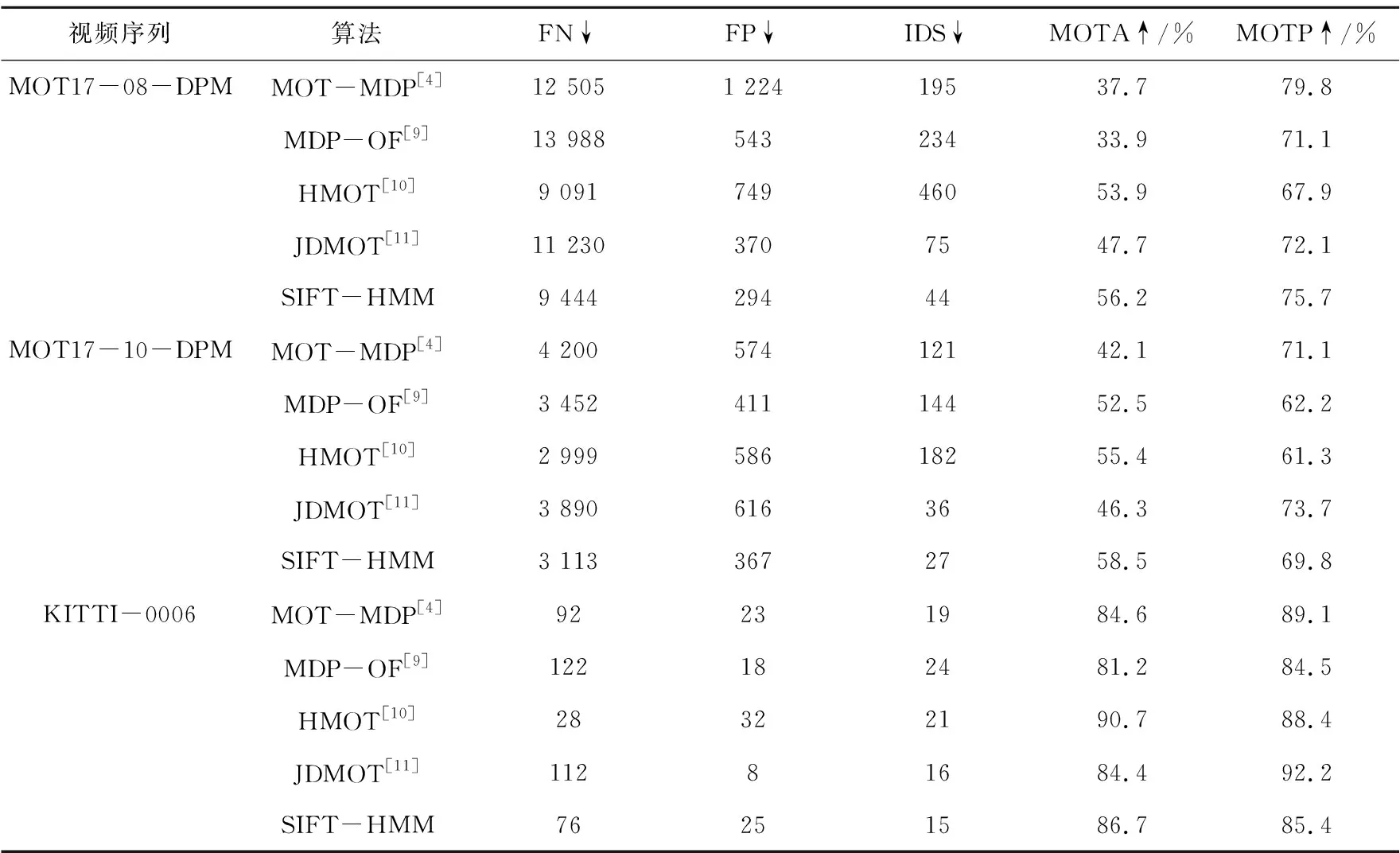
表2 与其他跟踪算法的对比结果

MOTA受FN、FP、IDS3个指标影响。HMOT算法在个体关联上引入了细化运动模式的方法，减少了算法的误阳性数据，在FN指标上有较好的效果，但在目标轨迹交叉时容易产生误差，IDS指标较差。本文的IDS指标在MOT数据集上平均比HMOT高7倍，在KITTI数据集上平均比HMOT高出42.7%。因此，本文在MOT17的两个序列上取得最好的性能，而在KITTI-0006序列上取得第二好的性能，比最好的HMOT算法低出4.6%。

本文的MOTP指标在MOT17-08-DPM取得第二好的性能，而在KITII数据集上取得第四的性能，这是因为以SIFT关键点建立HMM时，模型容易受背景特征点的干扰，导致框选目标时多框选了背景的特征点造成目标框与GT的不匹配。

4 结束语

本文提出了一种SIFT-HMM的多目标跟踪算法，该算法能够有效解决多目标跟踪过程的遮挡，以及目标身份互换的问题，在MOT20数据集上通过实验检验高维SIFT观测状态优越性，实验结果表明在视频序列首帧图像采用高维观测状态建立的SIFT-HMM，能够降低模型的复杂度。在MOT17和KITTI数据集上与其他跟踪算法进行了对比分析，对比结果表明，本文算法的IDS指标在两个数据集上表现最优，比第二优的算法高出34.3%和76.2%，表明本文的算法对目标身份互换问题有较好的鲁棒性；MOTA指标在2个数据集上分别取到56.84%和86.7%的性能，在MOT17数据集上比第二优的算法高出4.7%，表明本文的算法具有较好的跟踪准确度，并对遮挡问题有较好的鲁棒性。然而，本文在MOTP指标上未能表现最优，因此约束SIFT关键点来提高跟踪的精度会是未来研究的方向。