超声毛细效应的探究

徐浩翔，金 伟

(安徽师范大学 物理与电子信息学院，安徽 芜湖 241002)

2021年国际青年物理学家锦标赛(IYTP)第16题为超声波泵(Ustrosonic pump)：被浸入超声波水浴池中的毛细管可以像泵一样工作，将水提升到相当的高度，解释并探究这一现象. 在超声波作用下浸入液体的毛细管内液面高度反常上升的现象是由超声毛细效应导致的. 本文从挤压模效应和空化效应角度进行建模，分析超声毛细效应的原理，并探究影响超声波作用下毛细管内液面上升高度的因素.

1 预实验

图1为超声波泵的实验装置模型图.

图1 超声波泵实验装置模型图

在水槽中放入液体，水槽底部中心有超声波发生振子，用固定架将毛细管竖直固定在超声振子中央，并可以改变毛细管末端与振子的距离. 在预实验中，改变超声波的频率、液体的含气量和温度、毛细管的规格和其末端到超声波声源处的距离等因素，观察水柱高度的变化.

通过预实验，发现毛细管的内外径、超声波的频率和毛细管末端到声源的距离与水柱高度密切相关，其他因素(如液体温度、含气量等)也会产生较为明显的影响.

2 超声毛细效应的理论分析

2.1 挤压模效应的解释

首先从挤压模效应的角度建模. 在静水中未开启超声波发生器时，毛细管内液面上升主要是毛细现象[1]造成的. 这是固液表面的吸引力导致的现象，由注林定律[2]可知，静水中毛细管内液面上升的高度为

(1)

其中，hm为静水条件下管内液体较管外液面上升的高度，σ为液体的表面张力，θ为静止液体与毛细管管壁的接触角，ρ为液体密度，g为重力加速度，r2为管的内径.在毛细管表面和纯净水接触时，接触角近似为0.考虑液体压强平衡公式：

p=ρgh,

(2)

可以求得毛细作用下毛细管中产生的静压强为

(3)

当超声波发生器启动时，超声振子表面会产生高频率、小振幅的振动，这会引起毛细管底部产生附加静压力，即挤压模效应.毛细管末端与超声波发生器表面的截面图如图2所示.如果将静压力表示为振动引起的液体体积改变量的函数，在柱坐标系中进行近似计算，并引入挤压模因子α作为表征挤压模效应的常量，得到挤压模效应下附加静压强为[3]

图2 毛细管末端与超声波发生器的截面示意图

(4)

其中，r1和r2分别为毛细管的外内径，u为声速，A0为超声波的振幅，d0为毛细管末端距超声波发生器的距离.将式(4)代入式(2)，得到挤压模效应下毛细管内液面上升的高度为

(5)

因此挤压模效应下毛细管内液面上升的总高度值应为

(6)

2.2 辐射压与冲流的影响

超声波作用下毛细管内液体所受附加压强有2个分量：辐射压pr和冲流压ps[4].

由于声波在非理想介质中传播的非线性效应，声波入射到障碍物上会产生前向压强即辐射压pr[5].将声波在流体中的传播近似为绝热过程，又由于实验为封闭的管壁情形，则可以用瑞利辐射压来表示辐射压pr[6]，即

(7)

其中，γ为气体的比热容比，D为声场的声能密度.可以取声动能为

(8)

假设在声场作用下，声场引起的力做功为

Ep=-ΔpαΔV，

(9)

其中pα为激发声场的声压幅值.将体积改变量用密度变化表示，并假设密度变化量相对于ρ是高阶小量，可以得到声势能为

(10)

结合理想流体情况下小振幅波的状态方程以及声能密度的定义，可以得到声能密度为

(11)

代入式(7)，得出辐射压的大小为

(12)

从空泡动力学的角度考虑，空化效应导致的冲流压也是重要的影响因素之一.空化是在均质的液体中出现蒸气空泡，空化效应是水动力学领域的独特物理现象，可发生在任意流体中[7].

空化时产生的大量空化泡在破裂时会产生瞬间的高温和压强.空化泡从1个空化核膨胀至初始尺寸的若干倍后，空化泡将会在达到最大半径时破裂并附带有较小的气体分压.当大量空化泡破裂时，在毛细管内的液体中就会瞬间形成高速定向移动的冲流压ps.

分析空化泡在液体中的平衡条件. 假设在静止液体中处于平衡状态、半径为R(t)的类球状微小空化泡内含有空气和液体的蒸气.假设液体具有经受低于蒸气压pv乃至张力的能力,微气泡是液体开始破裂的薄弱点.假设在整个容器中压力是均匀的,故微气泡可视作球形.液体蒸气压与泡内空气压强之和为空化泡内部压强，即

pin=pv+pg.

(13)

类似地，可将空化泡外部的压强视为距空化泡较远处液体压强与气泡表面张力导致的压强二者之和，即

(14)

由此可以得出微气泡界面平衡的条件为

(15)

假设液体是不可压缩的牛顿流体并忽略重力作用,设泡内气体各项参量为常量且忽略惯性，忽略泡和周围液体的热交换即假设绝热过程，可推导出瑞利方程[8]，即

(16)

如果考虑黏性损耗，得到瑞利方程的修正式，即瑞利-普莱斯特方程：

(17)

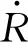
空化泡破裂的瞬间会向四周发射冲击波，其本质上是高压快速释放气体产生冲流.根据上述模型进行建模，可以得出蒸气泡破裂所产生的压力场满足：

(18)

由于大量空化泡破裂产生的冲流是定向的，因而可以认为只有毛细管内液面正下方的圆柱形区域内液体中的空化泡破裂产生的冲流压，才对液体上升产生影响.对圆柱体内的空化泡进行积分，可以用

(19)

计算冲流压的统计平均值，其中n为体积元内的空化泡数量.于是得到毛细管内液面上升的总高度为

(20)

2.3 挤压模效应和空化效应解释的联系

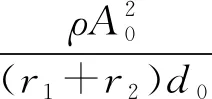
3 实验数据及分析

实验装置水槽内胆为240 mm ×135 mm×100 mm，选用内外径之和为0.5～10.0 mm的若干组硅胶管和玻璃管,超声波频率为20,28,40,50,68 kHz，液体选用蒸馏水与含气水.

选用频率为40 kHz、超声波功率为120 W、加热功率为100 W的超声波发生器，选用不同的d0值并改变内外径之和进行实验. 可以发现在实验范围内水柱高度与毛细管内外径之和呈现负相关，如图3所示,这与挤压模效应得出的结论一致. 当内外径之和增大时，如式(19)所示，冲流的贡献减小，冲流压也相应减小.

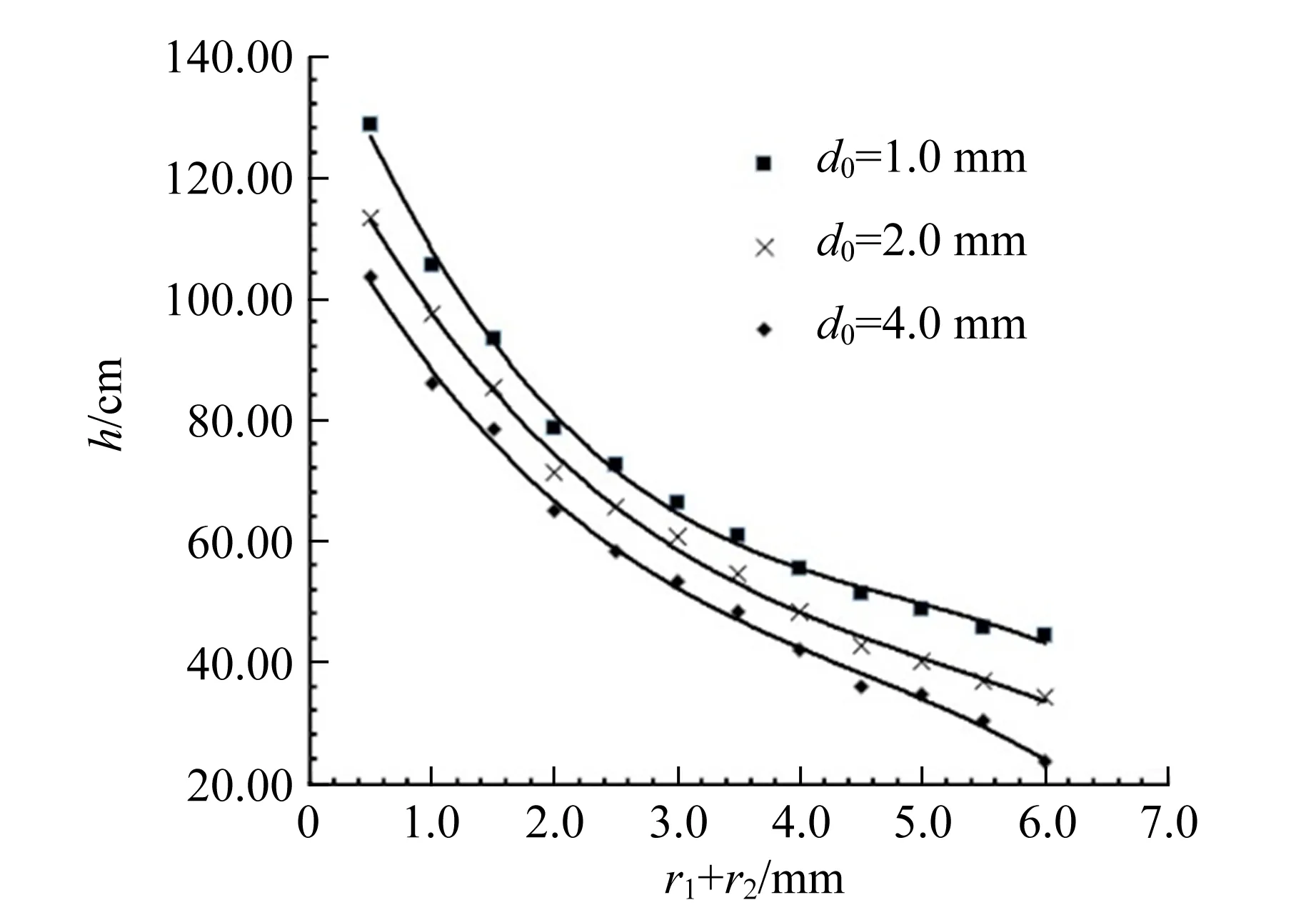
图3 水柱高度与毛细管内外径之和的关系

改变超声波频率，探究频率对超声波泵现象的影响.令d0≈1.5 mm，更换不同型号的超声波发生器,改变超声波的频率进行实验，如图4所示.可以发现在实验范围内毛细管内液面上升的高度随超声波频率的增大而减小.当频率增大时，膨胀时间相对变短，空化核来不及膨胀到破裂应有的尺寸，而压缩的时间又相对变短，空化泡来不及收缩破裂，因此难以发生剧烈的空化现象.由此可知，高频时空化效应较弱，此时的超声毛细效应主要由辐射压引起；低频时声波接近于球面波，空化现象较为明显，此时超声毛细效应主要由冲流压引起.

图4 水柱高度与超声波频率的关系

通过观察实验现象可以发现,毛细管距离声源处d0很微小时，才能观测到明显的现象，这是由于毛细管较远时超过了空化阈值所致[9].实验结果如图5所示，超声波作用下毛细管内液面高度的反常上升高度与毛细管底部到超声振子中心的距离呈现：先在0.5～0.7 mm内快速增加，之后液面高度与d0呈负相关.这是由于在极短距离内，随着距离增加空化泡的数量也会增加，冲流压的大小也就随之增加，此时空化效应占据主导地位，而挤压模效应的效果相对不明显；而当距离更大时，声波能量的衰减加剧，冲流压会随之减小，此时空化效应与挤压模效应的影响都相应减弱，水柱高度随d0的增大而减小.

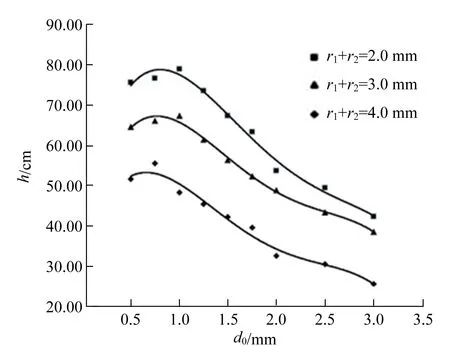
图5 水柱高度与d0的关系

通过改变液体温度来改变液体黏度的方式探究不同阻抗、具有不同声学特性的液体在超声毛细效应中的状况.实验表明：温度会对超声毛细效应产生较大的影响[10].但是温度因素较难探究，其原因在于超声振子工作时会在很短的时间内产生大量的热量，水槽内的温度场难以控制，因此采用降温的方式进行实验.实验过程中发现：在23 ℃附近，毛细管内液面会升高到极大值，而温度升高或降低都会导致现象的减弱，如图6所示.温度开始升高时，液体的黏度和表面张力系数下降，液体中空化核的数量增多，更容易产生空化泡并破裂；而当温度升高到一定程度后，液体蒸气压增大，空泡破裂产生的冲流压减小会导致空化强度减弱.但若仅从挤压模效应的角度来分析，随着温度的升高，液体黏度降低，挤压模因子α随之增大，挤压模效应变强.这说明挤压模效应对超声毛细效应的解释应当在考虑d0处液体的具体性质后进行合理修正.

图6 水柱高度与温度的关系

为探究液体含气量对实验的影响，选用蒸馏水与含气水进行对照实验，观察到含气水中超声毛细效应更加明显. 这是因为蒸馏水中缺少空化核，空化现象难以发生.

在选择合适的挤压模因子情况下，实验结果可以较好地符合挤压模效应的预测，且频率越高、液体黏度越大，则挤压模效应越明显. 但是当管道直径较宽时，无法用固定的挤压模因子来表达静压强与管道内外径之和的关系. 此外，对于超声波泵间隙内声阻抗和液体黏度对挤压模效应的影响，还应当求解间隙的流体动力学方程来计算实际的挤压模因子. 空化效应在各种情况下都可以较好地对超声毛细现象进行解释.

4 结 论

从空化的角度看，超声毛细效应主要是由于空化效应造成的大量空化泡破裂形成的定向冲流压，以及超声波作用下液体产生的辐射压共同导致的. 超声振子表面发生高频率、小振幅的振动引起毛细管底部产生附加静压力的挤压模效应也可以解释超声毛细效应. 通过实验证明了超声毛细效应导致的毛细管内液面高度反常增加与毛细管的内外径之和以及超声波频率呈负相关，与毛细管末端距离声源的间距以及温度的增加呈先增后减的关系. 另外，含气水中的超声毛细效应更明显.