浮沉子实验中不可逆现象的研究
2023-02-27孙金晶王鉴纯王春梅夏成杰
孙金晶,王鉴纯,王春梅,张 杰,夏成杰
(华东师范大学 物理与电子科学学院,上海 200241)
浮沉子是由法国科学家笛卡尔(1596—1650)创造的实验装置,作为趣味物理实验,常出现在科普演示与科学课外小组活动中,其实验材料易得,实验现象丰富,可以激发学生的学习兴趣. 2021年,第12届中国大学生物理学术竞赛(CUPT)题目6就与浮沉子直接相关,试题为:简单的浮沉子(例如部分装有水的倒置试管)被放置在装有水的长直管中,增加管中压强会使浮沉子下沉. 当浮沉子到达一定深度,即使改变管内压强至初始值,它都无法返回表面. 研究这一现象,以及相关参量如何影响该现象.
浮沉子体系看似简单,但实际涉及的物理机制较为复杂. 对于这一系统,不可逆现象是关键. 已经有文献给出其运动的基本理论[1-2]以及发生不可逆现象的临界条件[3],但是对于理论模型中的简化近似缺乏清晰的解释,也未能通过精确可控的实验加以验证. 为验证基础的理论模型和修正后的理论模型是否适用,结合浮沉子的特点,需要精确、可控的实验装置进行实验. 本文从浮沉子的制作、气压控制、图像处理等方面深入考虑,设计了有效且精确度高的装置及实验方法,从浮沉子运动和是否可逆等角度开展实验研究,所得实验结果与理论一致. 在对浮沉子问题的分析和解决过程中,既有理论分析的深化和完善,又有实验设计的修改和补充,还能综合运用Matlab等软件进行数值模拟、图像追踪处理,学生自主开展文献查阅和学习. 该过程对培养学生解决物理问题的能力具有重要作用,浮沉子适合作为本科生的初级科研训练,并融入大学物理实验课程[4].
1 实验原理
1.1 理论模型的构建
对浮沉子进行模型构建,实验参量及定义如图1所示.在此体系中,将浮沉子定义为倒置的试管及其内含的气柱,并且将二者作为整体进行受力分析.当管内压强p增大时,通过静水压强传递,浮沉子内部气体压强增大,体积减小,所受浮力减小.当压强p持续增大,浮沉子所受浮力减小直至小于重力与表面张力之和,浮沉子开始下沉.
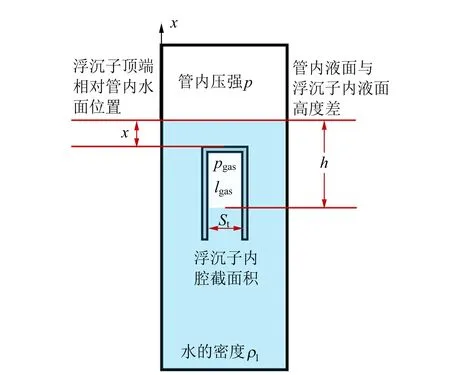
(a)装水长管及其内部的试管
1.2 浮沉子中气柱状态分析及受力分析
实际实验中,浮沉子内气柱压强为
pgas=p0+ρlgh+pd,
(1)
其中,pd为由流体运动而产生的压强.利用Comsol软件进行数值模拟,发现当浮沉子的运动速度在符合实际实验的±0.3 m/s范围内且加速度小于0.1 m/s2的情况下,运动流体产生的压力仅为重力的3%,可以将其忽略. 此外,分别使用理想气体状态方程的等温和绝热过程以及范德瓦尔斯方程,计算当气柱体积变化0.5 cm3时的体积-压强变化曲线(图2),发现在实验条件下,由不同的状态方程和热力学过程计算出的压强-体积关系的区别不大.
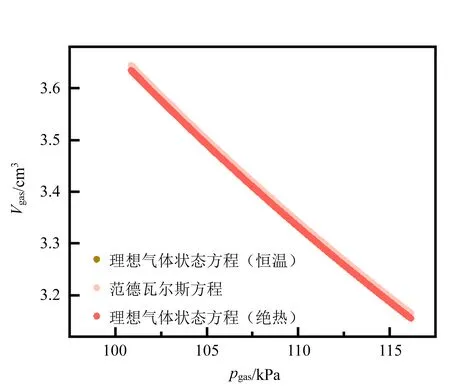
图2 数值计算浮沉子气柱体积随压强变化
因此,浮沉子内气柱在浮沉子运动的全过程中可近似看作发生等温变化的理想气体,由理想气体状态方程得到:
p0V0=pgasVgas=(p+ρlgh)lgasSt,
(2)
从而解得气柱长度为
(3)
分类讨论完全浸没与未完全浸没的情况下,计算得到浮沉子所受浮力为
Fb(x)=ρlgV排=
(4)
需要指出,在这里采用了静态液体中的浮力表达式,严格来说,它与在流体中运动的物体所受浮力存在区别.在下文计算浮沉子的运动过程中,将运动流体对物体额外的作用力以唯象的形式加入.通过将理论计算结果与实验数据对比,该近似非常合理.
在上述近似下,浮力是深度的函数,所以引入浮力与重力之和的等效势能[3]:

(5)
将不同管内压强下,浮沉子所受到的重力、浮力以及等效势能随其位置x的函数关系绘制如图3所示,其中各参量取值均符合实验实际情况.
图3展示了管内压强增加时浮沉子的运动全过程:压强增大,势能曲线中的极小值点在某临界压强下(1.08p0)消失,此时浮沉子开始下沉.此过程中势能曲线极小值点消失的过程也是较为常见的物理现象——折叠突变现象(Fold catastrophe)[3,5].当管内压强恢复初始的标准大气压时,势能曲线出现极大值(即势垒).若此时下沉的浮沉子已越过势垒或者其动能可使之越过势垒,则将继续下沉;反之将上浮.浮沉子在势垒位置所对应的深度的浮力满足
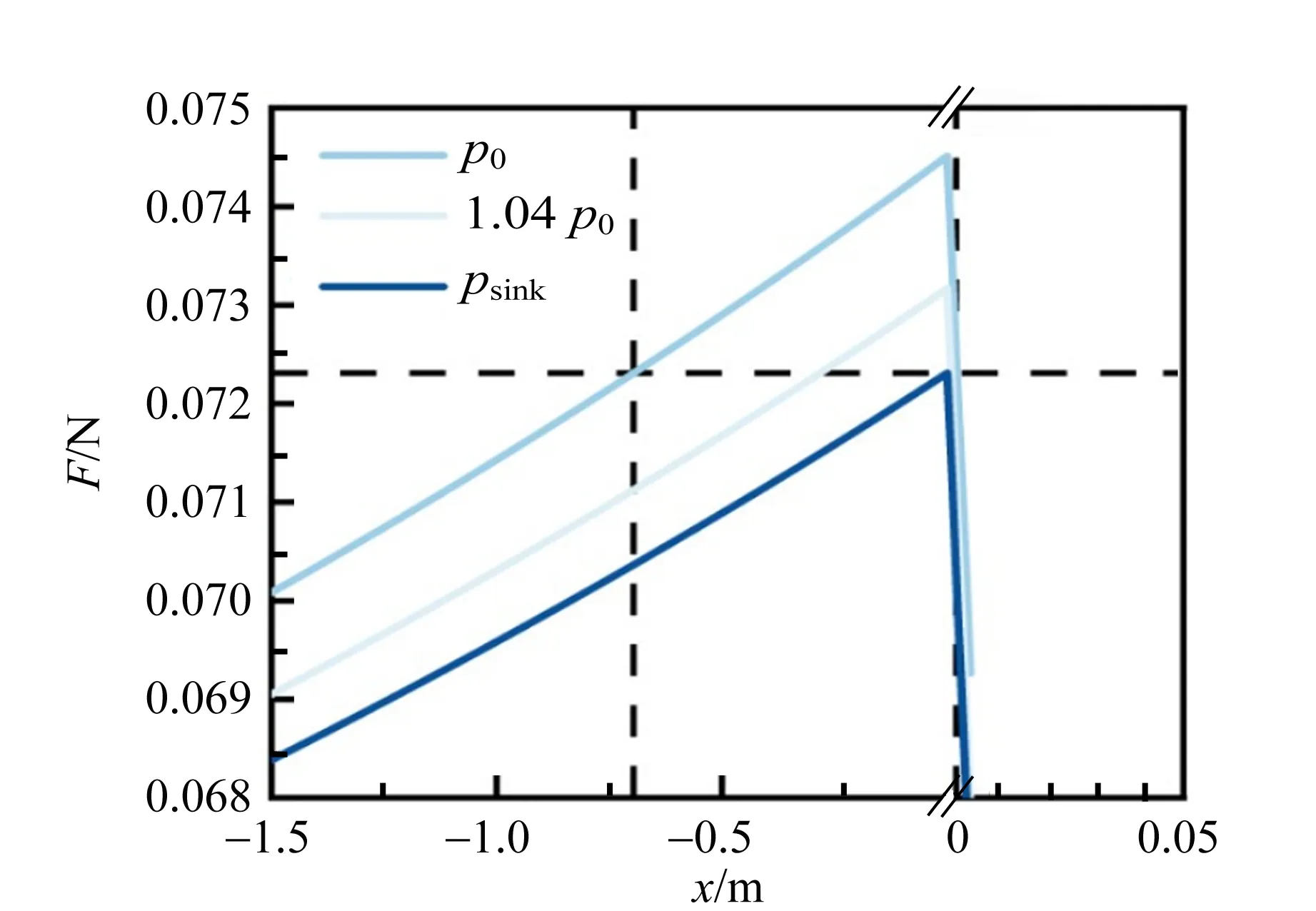
(a)重力与浮力
Fb=mg,
(6)
将此深度定义为临界深度.联立式(4)和(6),解得临界深度为
(7)
1.3 浮沉子的动力学分析
结合牛顿第二定律,浮沉子的动力学方程可以表述为
(8)
其中,fl表示运动的浮沉子所受到的流体阻力.虽然其严格的表达形式需要用复杂的流体力学计算,但是对比实验、理论和模拟计算均表明,使用斯托克斯经验公式计算当前体系中的流体阻力,能够较好地解释实验现象.除此之外,浮沉子在水面附近运动时还会受到表面张力作用,其具体大小不易测量[6-7],但是结合实验数据进行计算,发现表面张力比重力、浮力等主要作用力小2个数量级,因此可以被忽略.代入浮沉子和气压的相关参量,数值求解式(8),得到不同加压持续时间下,浮沉子的x-t和v-t图像(图4),其中x=0表示浮沉子的初始深度.
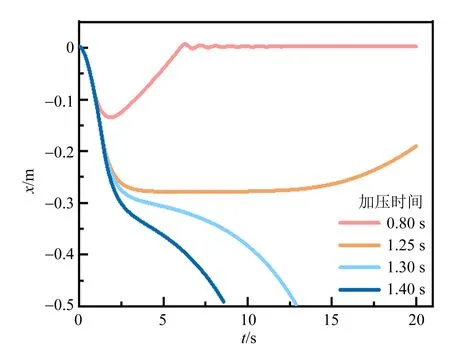
(a)x-t关系
从数值计算结果中可以看出,如果浮沉子在水下运动速度为0的深度小于临界深度,则最终会上浮,如图4中加压0.80 s和1.25 s情况;若大于临界深度,则最终沉底,对应于图4中加压1.30 s和1.40 s的情况. 并且可以看出,在最终上浮或下沉的临界情况附近,浮沉子的运动对加压过程的持续时间非常敏感:1.25 s和1.30 s的加压持续时间只改变了0.05 s,浮沉子只在临界深度附近停留了几秒,便表现出截然不同的后续运动情况. 这也反映了在图3势能曲线中,临界深度对应于非稳定平衡点的事实.
上述理论分析表明:由于实验环境中的各种扰动、实验仪器响应时间以及实验人员的反应时间限制,原则上不可能控制浮沉子恰好静止于不稳定平衡点,即无法通过调整参量而将浮沉子正好控制在临界深度附近并加以测量. 因此,必须通过不断改变参量,使浮沉子尽量接近临界深度的夹逼方法来测定临界深度.
2 实验装置及方法
2.1 实验装置
实验装置如图5所示. 使用铝型材搭建支架,用来固定亚克力长管并保证其竖直,上方的铝型材可压实橡胶塞以保证装置气密性良好. 橡胶塞连接2根玻璃导管,一根通过橡皮管与注射器相连,并采用可控参量的注射泵推动注射器以精确控制长管内的压强,可设定每次实验的注入速度和注入量,减小人为操作的误差;另一根玻璃导管通过橡皮管连接数显压差计,实时获取管内气压和大气压的差值,并用电脑记录,从而获取实验过程中管内气压随时间的变化图像. 实验中使用的浮沉子是采用3D打印制作的平底试管,其几何形状的参量可以精确到0.1 mm;为了便于对浮沉子进行图像追踪与处理,在试管壁上做了黑色标记.
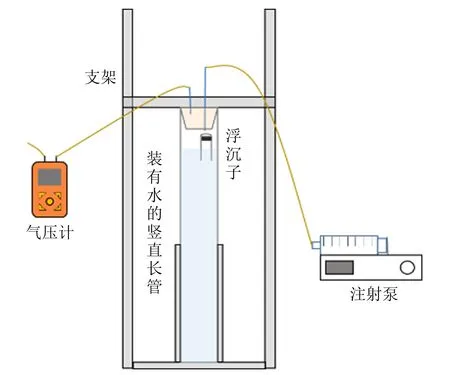
图5 实验装置示意图
2.2 图像处理
为获取浮沉子的位置数据,利用Matlab软件编写了图像处理程序. 在Matlab中导入视频并打开其中1帧图像,对视频图像进行二值化处理,得到浮沉子的黑色标记区域的二值图像,如图6所示,进而获取二值标定区域的最高位置坐标,结合图像像素大小与实际大小的定标数据,可换算得到浮沉子的位置.

图6 图像二值化处理示意图
为避免相机畸变引入定标误差,实验选取Nikon D810单反相机配置标准镜头,实验装置距离相机3 m,并且将图像呈现在相机画面的中间部分,装水长管横向视角小于1.5°,可以忽略横向畸变. 将装水长管的横向直径作为定标尺寸,利用像素换算获得图像中物体的测量长度. 长管的实际高度为1.500 m,经像素定标得到测量高度为(1.496±0.008) m,在误差允许范围内,可认为相机畸变对实验测量几乎无影响.
2.3 浮沉子运动全过程的探究
由3D打印制作不同参量的浮沉子样品,并精确测量其实际大小. 用注射器向浮沉子内注入一定体积的水,放入装有水的长直管中. 初始管内空气与外部连通,为1个大气压,随后固定橡胶塞及上方铝型材,以保持管内气体密闭. 启动压差计,开启相机,启动注射泵. 加压一定时间后,浮沉子开始持续下沉,暂停注射泵以保持管内压强恒定. 当浮沉子运动到一定深度,快速断开连接注射器的橡皮管,使长管内迅速恢复初始的标准大气压,浮沉子上浮或者继续下沉. 持续拍摄直至浮沉子运动结束. 最后,利用图像处理程序提取视频数据,得到浮沉子运动全过程的深度-时间图像.
2.4 临界深度的测量
由于浮沉子的临界深度为不稳定平衡点,原则上不可能使浮沉子长时间停留在临界深度所对应的位置,因此无法直接测量临界深度. 依据1.3探讨的情况,临界深度是决定浮沉子最终上浮或者下沉的直观物理量:最终上浮的浮沉子势必无法达到并且跨越临界深度,而最终沉底的浮沉子则势必跨越临界深度. 所以,对同一初始条件的浮沉子多次改变加压持续时间,得到多条上浮、下沉的深度-时间图像,通过不断夹逼的方式得到临界深度的范围,即浮沉子最终上浮的最深处和下沉的最浅位置的范围. 每组参量进行10次重复实验,实验测得的临界深度标准差为±5 cm. 该方法符合物理过程,是较为理想的临界深度测量方法.
3 实验结果及分析
实验所用浮沉子参量如表1所示.
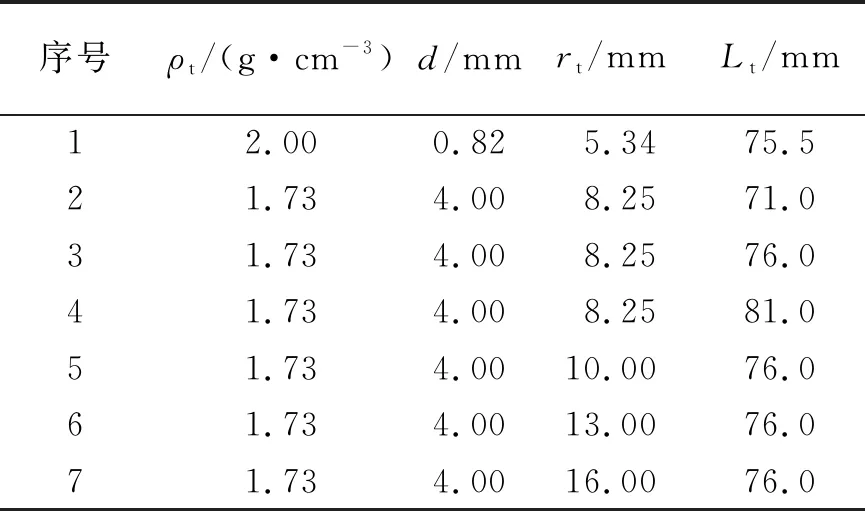
表1 实验所用浮沉子参量
3.1 阻力系数的获得
利用Comsol软件,采用圆柱形气柱在液体中的受力模型(图7),代入实际测量的实验参量,数值模拟得到斯托克斯公式的相关阻力系数为0.092.
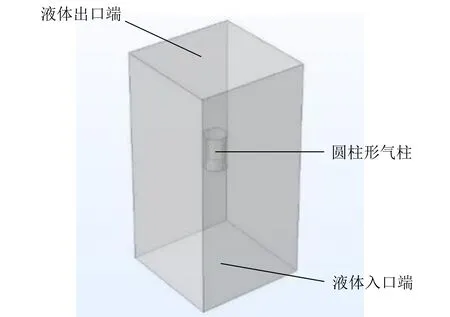
图7 Comsol模型计算阻力系数
3.2 加压持续时间对浮沉子运动的影响
通过改变停止加压到恢复初始气压的间隔时间来改变加压持续时间,得到不同加压持续时间下浮沉子的运动过程. 实验结果如图8所示,在恢复压强后浮沉子运动情况与理论对照非常一致,同时,相同条件的实验现象可重复性较高,均符合临界深度判定,且理论临界深度与实验夹逼范围一致. 本实验的合理性得到验证,实验与理论结果较为吻合.
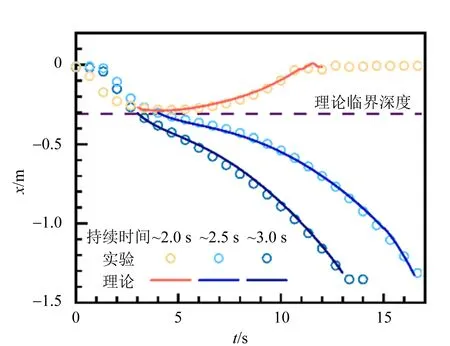
图8 浮沉子不同运动的实验与理论对比
3.3 各参量对临界深度的影响
基于上述装置和实验处理系统,本实验还探究了初始气柱长度、浮沉子长度和浮沉子内截面积等参量对浮沉子临界深度的影响,如图9~12所示. 由1.2可知,临界深度满足式(7),临界深度随各参量改变的实验结论如下:浮沉子初始气柱长度越大,临界深度越深,二者基本呈线性关系;实验范围内,浮沉子长度越小,临界深度越深;实验范围内,浮沉子截面积越大,临界深度越深.
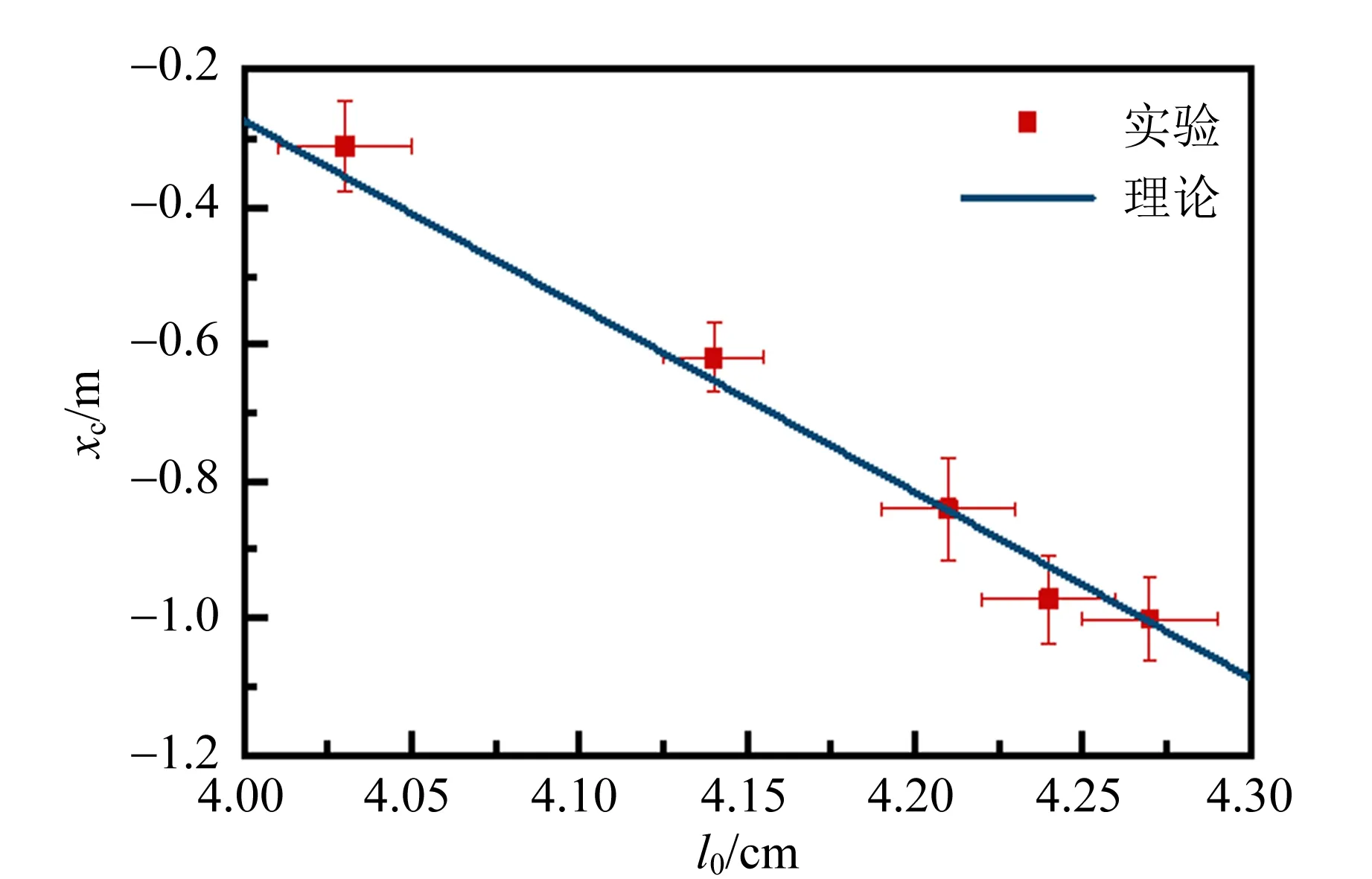
图9 初始气柱长度对临界深度的影响 (浮沉子1)
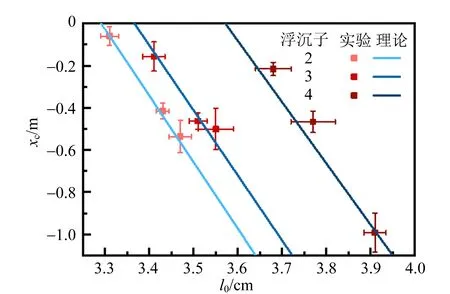
图10 浮沉子长度对临界深度的影响
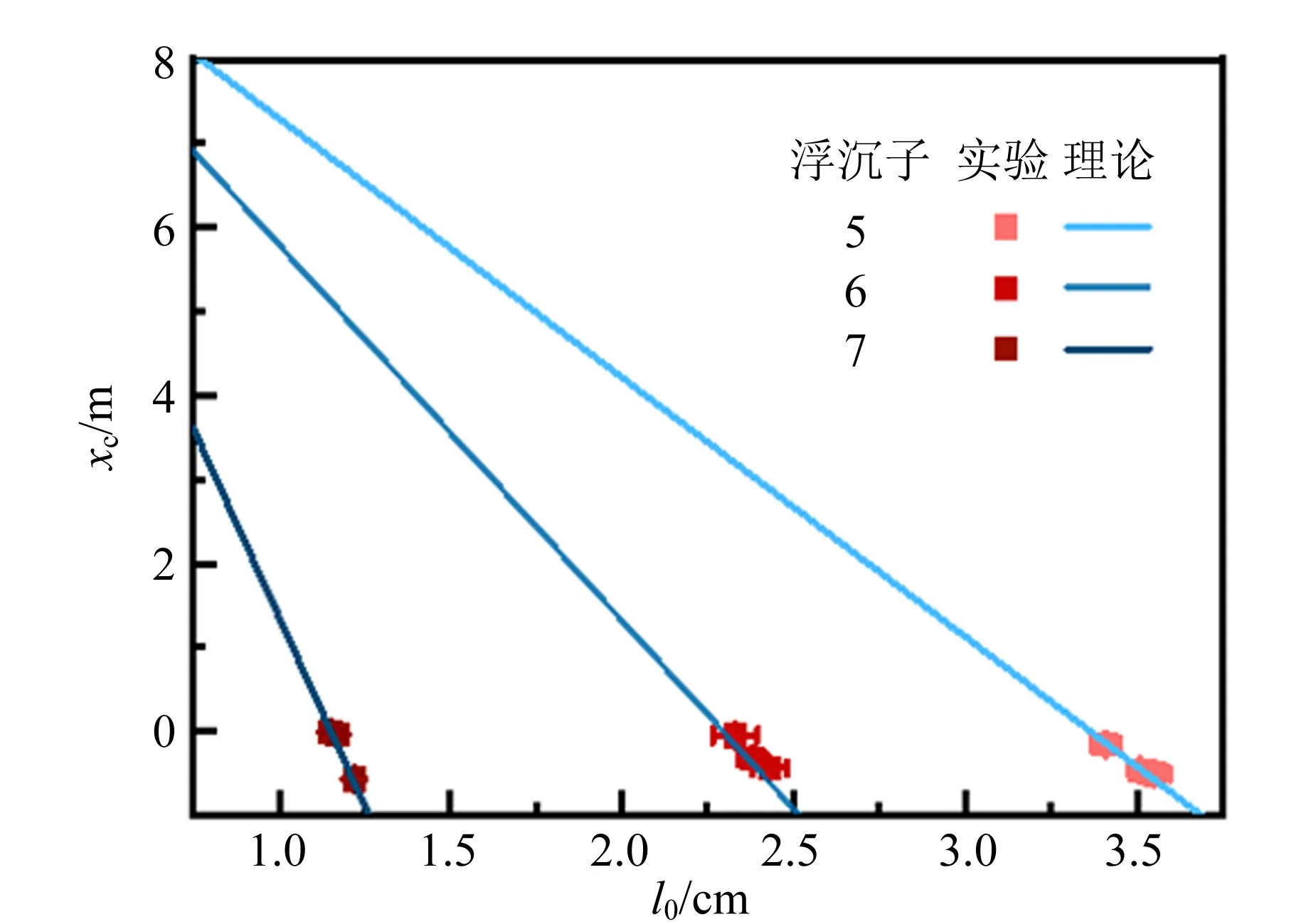
图11 浮沉子截面积对临界深度的影响
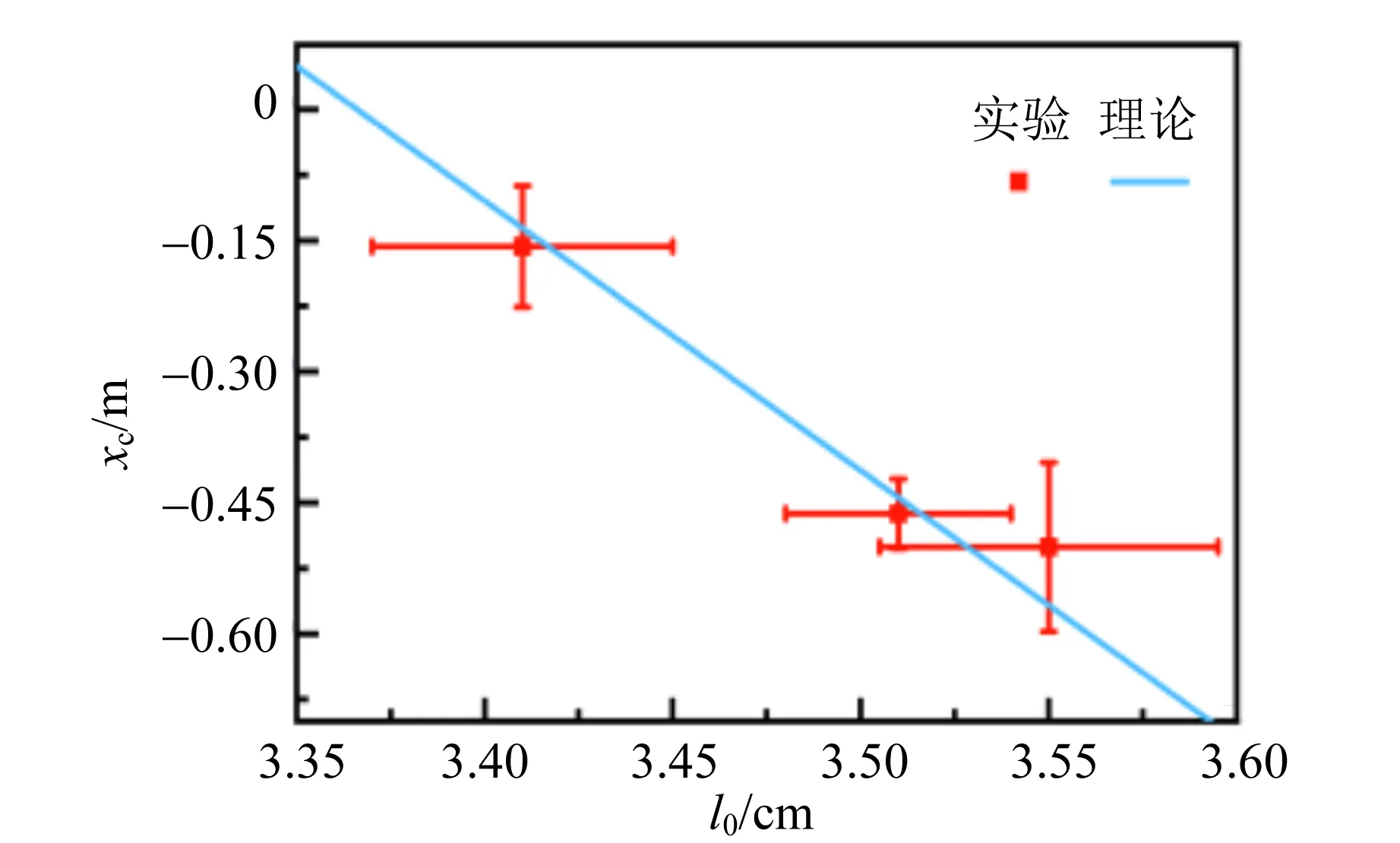
(a)浮沉子5
初始气柱长度误差棒(横向)主要表征对气柱长度进行追踪带来的误差,即由于测量气柱长度所占用的像素点数量较小,且液体边界较为模糊,因此引入误差棒表示测量精度;临界深度误差棒(纵向)用以体现夹逼法确认临界深度时产生的误差,其上下界代表夹逼的范围以及长度测量的误差. 在误差允许的范围内,实验结果与理论符合.
4 结束语
本文设计了参量可控的装置以及配套的实验方法和图像数据处理方法,并研究了浮沉子的运动过程,利用夹逼的方法获得了浮沉子不可逆现象的临界深度,且研究了影响临界深度的多个参量,验证了基础的理论模型和修正后的理论模型的适用性. 该实验操作简单,理论思路清晰,可以作为大学物理实验的拓展内容,培养学生分析、研究与解决问题的能力,实验操作能力,资源获取、整合以及综合运用的能力.
