基于曼哈顿距离检测的马铃薯畸形识别

于莹，王关平，王成江，韦昱伶

（730070 甘肃省 兰州市 甘肃农业大学 机电工程学院）

0 引言

畸形是马铃薯较为常见的生理形态改变，会影响其商品性状，大大降低了经济收益[1]，因此马铃薯收获后对畸形薯的售前识别与筛选分选非常重要。目前，国内外已实现较为可靠的机械式分选，其技术路线有滚筒式[2]、网眼式[3]、链板辊轴式[4]等。然而，一方面，这些系统立足于简单廉价，不仅存在着分级粗略、变换困难、实用性较差等问题；另一方面，还可能诱发分拣中薯块的二次损伤，且缺乏剔除伤、坏薯的基本能力，更不可能完成畸形薯的辨识和甄选。目前，国内外的畸形薯去除依然主要依靠人工目测，手动捡拾。该过程劳动强度大、成本投入高且效率低下，因此采用自动化系统替代人工便成为当务之急。基于简单传感器构建的检测系统，往往只能获取马铃薯尺寸、质量等粗略信息[5]，使得畸形识别这类复杂判断因信息匮乏而难以开展，因此能否获得足够信息量成为畸形辨识的关键所在。基于机器视觉的深度分析为诸多实际需求提供了大量数据，使许多原先的不可能成为现实[6-7]，已经有部分学者将机器视觉应用于农业生产的诸多环节[8]。

针对马铃薯畸形的智能识别，史崇升[9]基于高光谱技术首先进行了畸形识别尝试；张保华[10]等借助I-RELIEF 模块将带有权值的形状特征样本放入SVM 模块中训练并得到分类器，实现了较为有效的辨识，但算法较为复杂；汪成龙等[11]在此工作的启发下，对SVM 分类器进行了改进，只需提取10 个形状特征的傅里叶权值训练即可，使得畸形识别的方法简单化，可靠性可以达到90%以上。为追求更准确的识别方法，许伟栋等[12]提出PCA-SVM 算法提取形状特征参数建模进行马铃薯形状分类，准确率已高达97.3%。但是，上述工作依然需要大量计算，且基本都停留在实验室阶段。

本文提出一个简单实用的方法识别解决马铃薯畸形问题，基于距离检测[13]的曼哈顿距离检测法计算马铃薯边缘轮廓形状与最小外接圆间距离，依据测量距离值绘制曲线图检测马铃薯形状是否畸形。

1 图像预处理

本文使用OpenCV 库Python 对采集的马铃薯进行灰度处理，获取马铃薯灰度图像，进而对灰度图像二值化处理，获得二值化图像。与此同时，检测马铃薯轮廓并画出边缘轮廓的最小外接圆曲线，形态学腐蚀得到轮廓曲线，为马铃薯畸形识别做出准备。

1.1 图像采集

马铃薯品种选自于甘肃省兰州市榆中县出产的陇薯9 号、青薯7 号，采用尼康D7500 单反相机，23.55 mm×15.7 mm CMOS 传感器，连拍速度8 张/s，在同一角度、统一高度下拍摄采集马铃薯图像，共采集正常形状马铃薯图、畸形马铃薯图像各170 张，总计340 张图片。马铃薯形状示意图如图1 所示。图像处理软件使用Python3.7.0、编译器PyCharm、Anaconda 创建虚拟环境TensorFlow2.0。

图1 马铃薯形状示意图Fig.1 Schematic diagram of potato shape

1.2 图像预处理

首先，对采集的马铃薯原图片灰度处理，这也是将马铃薯彩色图像R、G、B 等量化的过程。灰度图像每个像素点只存放一个字节灰度值，范围0～255，显示的灰度图像通常用每个采样像素8 位的非像素尺度保存，避免条带失真，易于后续的图像处理。由于RGB 模式不能准确体现图像的具体形态特征，而且肉眼对图像绿色敏感度较高，蓝色敏感度较低，因此选取加权平均法对图片灰度处理。加权平均法公式为：

Gray（i，j）=a×R（i，j）+b×G（i，j）+c×B（i，j）(1)式中：Gray（i，j）——灰度值；R（i，j），G（i，j），B（i，j）——图像中红、绿、蓝三基色分量像素；a，b，c——灰度公式中的系数，通常为固定值a=0.299，b=0.578，c=0.114。

为更好地凸显出马铃薯轮廓，要将图像二值化处理分析，一般采用封闭、连通的边界定义不交叠区域，使用thresh_binary 函数对图像进行阈值二值化处理。像素值大于阈值135 的用255（黑色）表示，小于阈值135 用0（白色）表示。对处理好的二值化图片使用cv2.findcontours()函数的cv2.RETR_EXTERNAL 模式检索寻找马铃薯图像最外层轮廓，并用cv2.CHAIN_APPROX_NONE 保留轮廓线上的所有坐标。由函数cv2.minEnclorsingCircle返回马铃薯圆心坐标和半径组成的二元组，再令drawcontours 函数绘制马铃薯边界轮廓的最小外接圆。最后，对已获取最小外接圆轮廓的马铃薯二值化图像进行形态学腐蚀，继而使用Python 库scikitimage canny 边缘检测提取马铃薯自身形状与最小外接圆双层轮廓。马铃薯预处理图像如图2 所示。

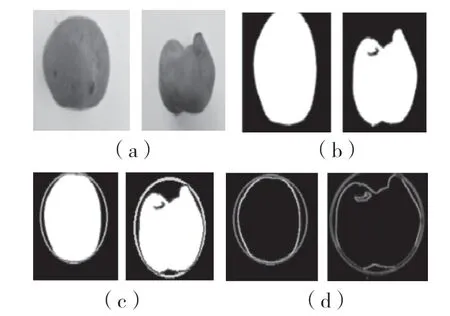
图2 马铃薯预处理示意图Fig.2 Schematic diagram of potato pretreatment

2 实验方法

2.1 坐标矩阵

马铃薯图像的边缘轮廓是由连续的点组成，因此contours 查找图片轮廓并遍历图片中所有轮廓层。用迭代器输出检测到双层轮廓层线上的全部二维坐标点，使其形成一个2 行n 列的二维坐标矩阵，并计算坐标矩阵中每列两点之间的距离值，再用Python PandaS 库将距离值批量写入csv 文件，再访问读取csv 文本中数据，绘制出马铃薯自身轮廓与最小外接圆间曼哈顿距离数据值曲线图。

2.2 曼哈顿距离检测法

曼哈顿距离也称作城市街区距离，19 世纪由赫尔曼·闵可夫斯基创立，应用于几何度量空间。如二维平面上有两点A1（X1，Y1），B1（X2，Y2），两点在二维标准坐标系上的绝对轴总和（坐标轴上的投影）D 称作两点间的曼哈顿距离。曼哈顿距离计算二维坐标公式为：

曼哈顿距离检测法优点在于计算速度快、适用于整数计算，但是在距离检测算法中被高频率使用的是欧几里得距离，也称欧氏距离，表达为m 维空间内两点直线距离D 称为度量空间。二维平面上两点之间欧式距离为

假设马铃薯自身形状轮廓层线上输出n 个二维坐标点，n 个坐标点组成一行n 列矩阵P1，P1=[X1i，X1j]（i，j∈（1，n））；马铃薯最小外接圆轮廓层线上输出的二维坐标形成一行n 列矩阵为P2，P2=[X2i，X2j]（i，j∈（1，n））。2 个 矩阵P1，P2构成一个新的2 行n 列二维坐标矩阵P：

测量二维坐标矩阵P 中每一列上下相对应点坐标（X1i，X1j），（X2i，X2j）间的曼哈顿距离d：

测量轮廓间曼哈顿距离值示意图如图3 所示。

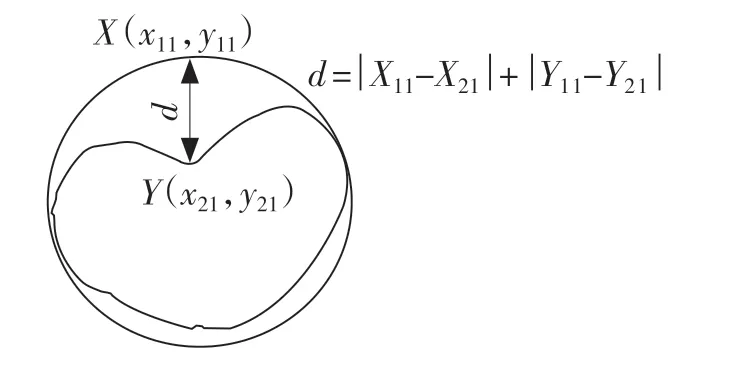
图3 马铃薯轮廓间曼哈顿距离检测示意图Fig.3 Detection of Manhattan distance between potato contours

由于轮廓曲线上有n 组相对应的坐标组，数据值过多，因此从测得所有坐标点间的曼哈顿距离值中选取数值差距较为明显的距离值存入csv 文本中，共选取33 组坐标点，再用Python 读取csv 文本中的数据（测量的距离值），设定x 轴为从坐标矩阵中选取的33 组坐标点，y 轴为马铃薯双层轮廓对应坐标点间的距离差值，绘制二维坐标点间的距离曲线图。通过观察二维坐标曲线图的曲线趋势、形状，以及波峰波谷的数量判断马铃薯是否畸形。正常马铃薯坐标曲线如图4（a）所示，畸形马铃薯坐标曲线如图4（b）所示。

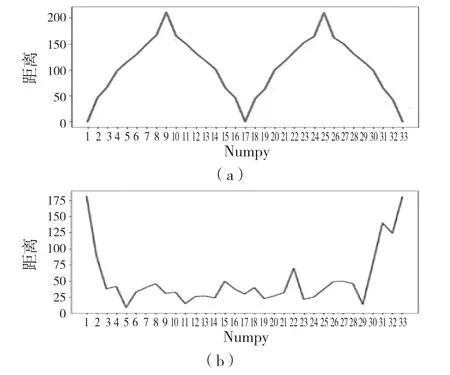
图4 马铃薯图像曼哈顿距离曲线特征Fig.4 Characteristics of Manhattan distance curve of potato image

3 实验与分析

3.1 实验方法对比

在以往的实验中，距离检测方法中通常采用欧氏距离进行数据检测[14]。欧式距离的优点在于简单、易操作。但是，使用欧式距离测量坐标点间距离时必须使用浮点运算。然而，在机器视觉图像识别过程中，图像的像素点坐标可能会是整数，显然欧式距离不适用。而且，计算机进行浮点运算时速度较慢、有误差，每个坐标点的坐标对欧氏距离贡献是等价的，当坐标轴表达测量的数值时，会产生不同大小的随机波动[15]。此时需对坐标加权，使变化较大的坐标比变化较小的坐标有较小的加权系数，随机波动的后果便是产生各种距离，若特征值大小有明显差距会降低测量精度，稳定性能不高，不能满足实验的实际需求。相对比较之下，曼哈顿距离检测法不仅测量的运行速度快、稳定性能高，还可以减少欧氏距离在开方运算过程中带来的误差，只需将二维坐标点相减即可得到需要的测量值，快捷、简便，因此选取曼哈顿法检测坐标矩阵中相对应点间距离对马铃薯畸形识别。

3.2 数据分析

实验过程中共处理马铃薯图片340 张，畸形薯和正常薯各170 张。选取70 张正常薯、70 张畸形薯作为数据集，正常薯和畸形薯各100 张作为测试集。根据实验数据发现，正常薯的曲线图多数只有两个波峰且波峰差值较小，最多有3 个波峰，而畸形薯的曲线特征趋势较为抖动，波峰全部多于3 个，波峰最大值与最小值间差值较大。表1 为马铃薯自身形状与最小外接圆双层轮廓间距离差值。实验结果分析发现，畸形薯波峰最大值与最小值之间差值的平均值较大，波峰差值方差是正常薯的17 倍，标准差是正常薯形的3.56 倍，可见畸形薯波形图极为不稳定。为更好地识别畸形薯，将正常薯的平均值加3 个标准差确定为判断马铃薯是否畸形的依据。δ=x+3σ即阈值设定在σ=36.18，φ为马铃薯曲线图波峰最大值与最小值间差值：

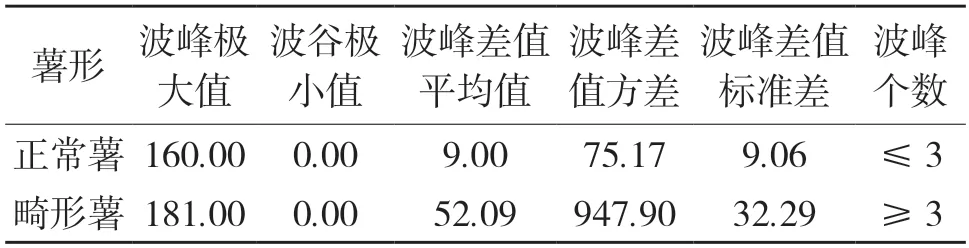
表1 马铃薯自形状与最小外接圆间距离值Tab.1 Distance between the potato shape and the smallest peripheral circle

由此可见曼哈顿距离检测法可以有效解决马铃薯畸形识别问题。畸形马铃薯形状不规则提取的边缘轮廓与外接圆轮廓间距离值之差较大，形状特征曲线也较为明显，而较规则的正常马铃薯形状轮廓特征与外接圆轮廓特征之间距离值曲线特征较为规律。多数坐标曲线图明显呈对称状，但是在遍历轮廓层提取轮廓线上坐标点时发现，各别图像的某几个点的像素坐标被提取时会出现误差，导致距离曲线图并无明显对称或呈现不规率曲线被系统误判为畸形，因此整体识别率为91.50%。

表2 马铃薯畸形识别Tab.2 Identification of potato malformation

4 结论

马铃薯形状畸形会降低马铃薯的商品属性，导致马铃薯加工利用率低，工业化加工转化率仅为5%[16]，因而在播种和收获过程中需将畸形马铃薯逐个挑出，降低马铃薯价值损耗[17]。

本文使用曼哈顿距离法对马铃薯进行畸形识别，实验过程发现曼哈顿距离检测法精度高，减少了欧式距离检测方法中由于开方产生的误差。采集马铃薯图像预处理，由于获取图像最小外接圆轮廓的前提是图像必须为二值化模式，因此需对图片灰度处理。提取马铃薯边缘轮廓，按照边缘轮廓的点集使用minEnclosingCircle 画出边缘轮廓最小外接圆。应用形态学腐蚀canny 算法提取马铃薯所有轮廓层，遍历所有轮廓层并输出轮廓线上坐标点，构成坐标矩阵。使用曼哈顿距离法测量轮廓层对应点间的距离值，根据测得的距离值画出坐标曲线图，如果曲线波形图的形状对称、规则，且马铃薯波峰间差值在设定的阈值范围内、波峰数量≤ 3，则马铃薯形状为正常薯，否则为畸形薯。根据实验数据测得马铃薯畸形识别率为96%，整体识别率91.5%，证明该方案可有效识别马铃薯形状畸形问题。